2021-2022学年高一下学期数学人教A版(2019)必修第二册8.6.2直线与平面垂直说课课件(共39张PPT)
文档属性
| 名称 | 2021-2022学年高一下学期数学人教A版(2019)必修第二册8.6.2直线与平面垂直说课课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 13.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-15 00:00:00 | ||
图片预览





文档简介
(共39张PPT)
8.6.2 直线与平面垂直(第1课时)
“整章-单元-课时”说课
目录
CONTENTS
01
整章分析
02
单元内容及其解析
03
单元目标及其解析
04
单元教学问题诊断分析
05
单元教学条件支持分析
06
课时教学设计
01
整章分析
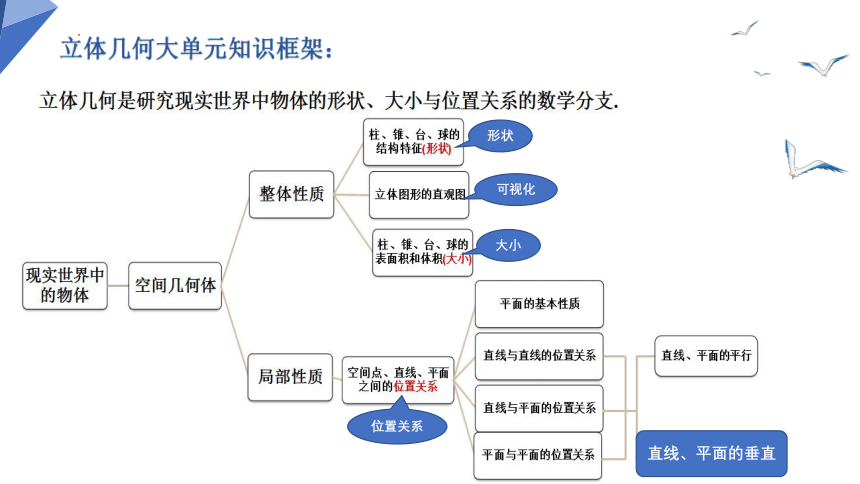
立体几何大单元知识框架:
直线、平面的垂直
形状
可视化
大小
位置关系
02
单元内容及其解析
直线、平面的垂直
知识的
上下位关系
内容本质
蕴含的数学思想
和方法
育人价值
教学重点
单元内容及其解析
内容
单元内容及其解析
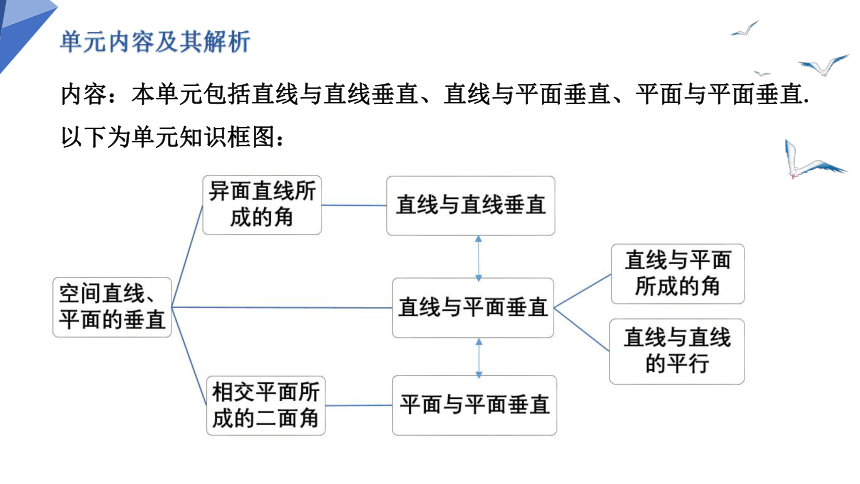
内容:本单元包括直线与直线垂直、直线与平面垂直、平面与平面垂直.
以下为单元知识框图:
单元内容及其解析
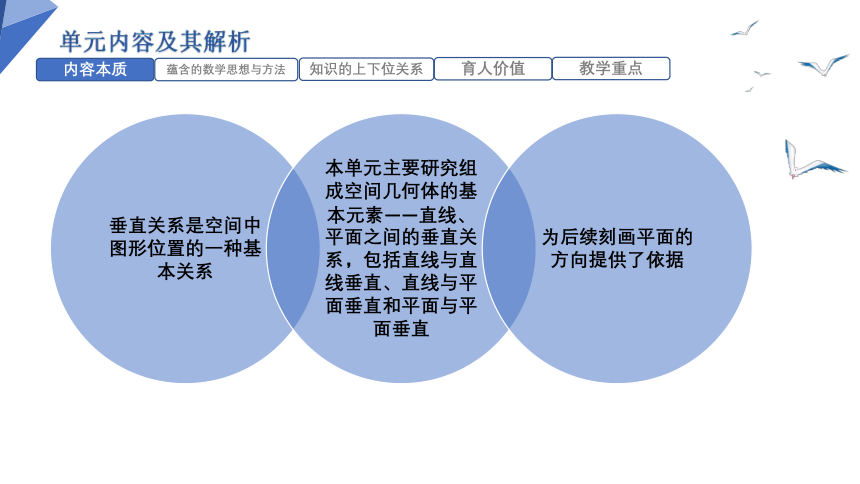
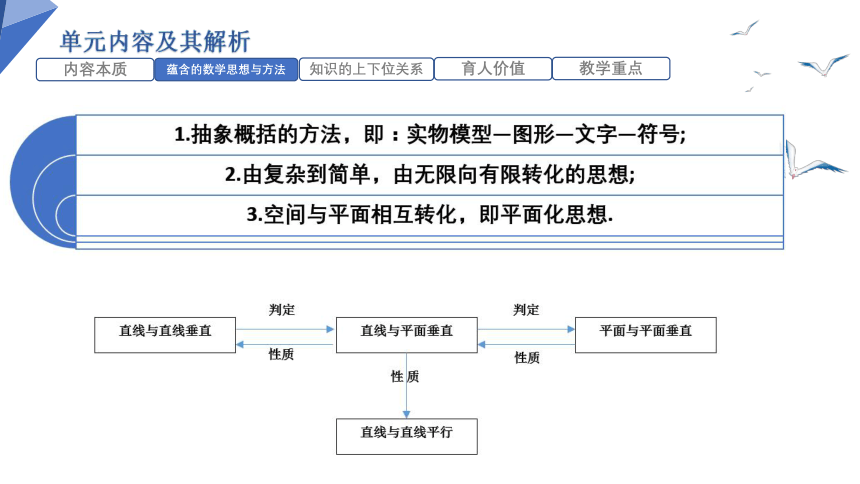
内容本质
蕴含的数学思想与方法
知识的上下位关系
育人价值
教学重点
单元内容及其解析
内容本质
蕴含的数学思想与方法
知识的上下位关系
育人价值
教学重点
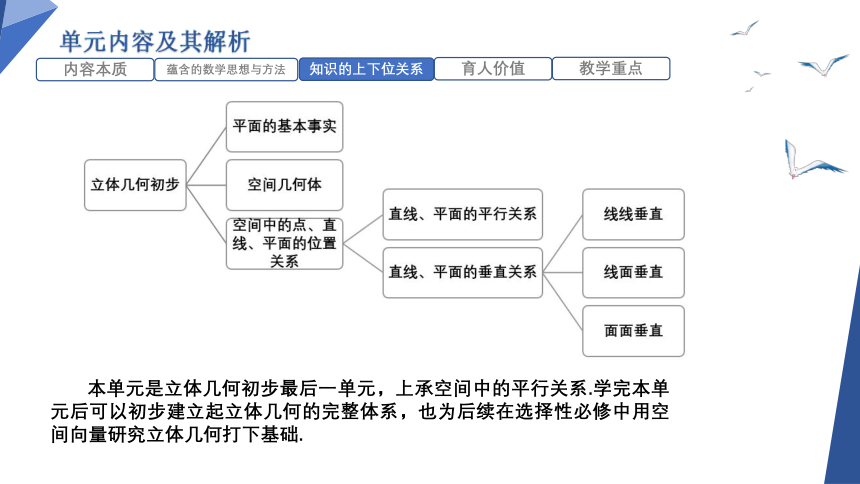
单元内容及其解析
内容本质
蕴含的数学思想与方法
知识的上下位关系
育人价值
教学重点
本单元是立体几何初步最后一单元,上承空间中的平行关系.学完本单元后可以初步建立起立体几何的完整体系,也为后续在选择性必修中用空间向量研究立体几何打下基础.
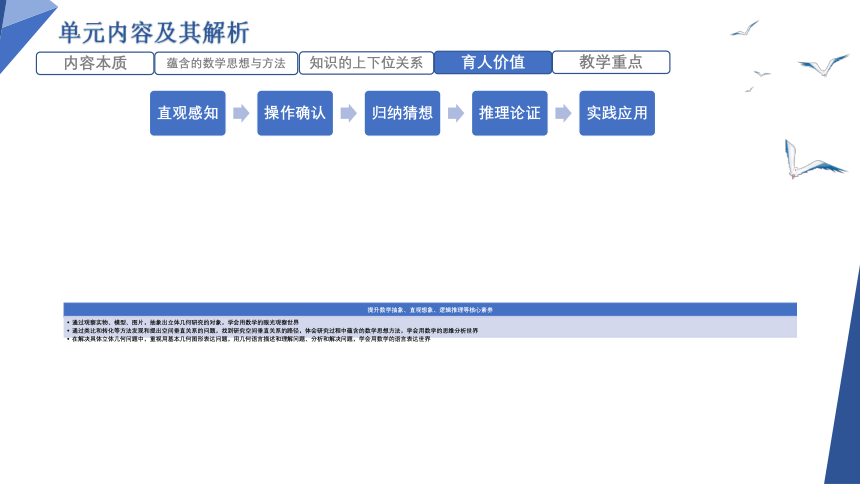
单元内容及其解析
内容本质
蕴含的数学思想与方法
知识的上下位关系
育人价值
教学重点
单元内容及其解析
内容本质
蕴含的数学思想与方法
知识的上下位关系
育人价值
教学重点
03
单元目标及其解析
单元目标及其解析:
04
单元教学问题诊断分析
单元教学问题诊断分析:
05
单元教学支持条件分析
生活实例、图片
GeoGebra软件
模型、三角形纸片等工具
智慧课堂等
教学支持条件
教学支持条件分析:
通过观察和展示现实生活中的实例与图片,可以很大程度促进学生直观感知直线、平面垂直的形象;
准备模型、三角形纸片等工具,用于探究定理;
利用GeoGebra软件或制作多媒体课件动态演示,加深对空间垂直关系的感知与理解
06
课时教学设计
课时教学设计案例
8.6.2 直线与平面垂直(第1课时)
课时教学设计案例
课时教学内容:直线与平面垂直的概念、判定定理
课时教学目标:(1)理解直线与平面垂直的意义、点到平面的距离;
(2)探索并了解直线与平面垂直的判定定理,能利用判定定理证明直线与平面垂直的简单问题;
(3)在探索直线与平面垂直判定定理的过程中发展合情推理能力、感悟和体验“空间问题转化为平面问题”“线面垂直转化为线线垂直”,进一步感悟数学中“以简驭繁”的转化思想.
课时教学内容
课时教学目标
教学重点
教学难点
教学过程设计
课时教学设计案例
教学重点:直线与平面垂直定义的抽象与归纳,以及直线与平面垂直判定定理的发现与验证.
教学难点:发现并验证直线与平面垂直的判定定理.
课时教学内容
课时教学目标
教学重点
教学难点
教学过程设计
课时教学设计案例
教学过程:五个环节
环节一:微课引入,单元框架
环节二:直观感知,归纳定义
环节三:操作确认,探究判定定理
环节四:推理论证,定理简单应用
环节五:课堂小结,课后作业
课时教学内容
课时教学目标
教学重点
教学难点
教学过程设计
课时教学设计案例
环节一:微课引入,单元框架
课时教学设计案例
环节一:微课引入,单元框架
问题1:类比平行的研究思路,接下来我们应该研究什么?
设计意图:借助微课梳理本章知识结构,同时回顾平行的研究思路,通过类比提出问题,明确本节课的研究内容和路径.
课时教学设计案例
旗杆与地面的位置关系
桥柱与水面的位置关系
设计意图:通过大量生活实例和图片加深学生对直线与平面垂直的感性认识,为后续引入用数学语言刻画生活中的直线与平面垂直做铺垫.
问题2:结合生活,请举出可以抽象成直线与平面垂直的具体实例.
环节二:直观感知,归纳定义
课时教学设计案例
环节二:直观感知,归纳定义
问题3:能否把直线与平面垂直的直观形象数学化,用明确的数学语言给出定义呢?结合旗杆例子进行探究.
思考1:阳光下,直立于地面的旗杆及它在地面的影子有何位置关系
思考2:随着太阳的移动,旗杆及它在地面的影子位置关系又是什么呢?
A
B
α
思考3:旗杆与地面上任意一条不过B点的直线位置关系又如何?
设计意图:为了用明确的数学语言下定义,借助三个思考进行突破.其中思考1和思考2说明了旗杆和平面内任意相交的直线垂直,思考3则说明了旗杆与平面内任意异面直线垂直.通过观察与思考把直观模糊的感性认识抽象化、确切化,顺势引导学生归纳概括出直线与平面垂直的定义.
B1
C1
C
B
课时教学设计案例
环节二:直观感知,归纳定义
直线与平面垂直的定义:
如果直线l 与平面α内的任意一条直线都垂直,我们就说直线l 与平面α互相垂直. 记作l⊥α
l
平面α的垂线
直线l 的垂面
A
垂足
课时教学设计案例
环节二:直观感知,归纳定义
(1)如果一条直线与一个平面垂直,那么这条直线与平面内任意一条直线都垂直.
(2)如果一条直线与一个平面垂直,那么这条直线与平面内无数条直线都垂直.
(3)如果一条直线与一个平面内的一条直线不垂直,那么这条直线与这个平面不垂直.
(4)过一点垂直于已知平面的直线有且只有一条.
过一点作垂直于已知平面的直线,则该点与垂足间的线段,叫做这个点到该平面的垂线段,垂线段的长度叫做点到该平面的距离.
设计意图:加深概念理解,掌握定义本质,明确任意一条与无数条的区别;通过判断(4)让学生直观感知该结论,进而给出垂线段、点到平面的距离的概念,顺势介绍棱锥的高的概念,从而实现了感性认识到理性认知的转变,弥补了结构特征单元中的概念不足.
课时教学设计案例
环节三:操作确认,探究判定定理
动手操作:
请同学们准备一块三角形的纸片,我们一起来做如图所示的试验:过△ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD、DC与桌面接触).
A
B
C
D
思考:(1)折痕AD与桌面垂直吗?
(2)如何翻折才能保证折痕AD与桌面所在平面α垂直?
设计意图:根据定义,判断直线与平面垂直,需要验证直线与平面内的所有直线都垂直,这是一个无限问题,难以操作.类比平面与平面平行的判定定理,需要寻求判定直线与平面垂直的简单、易行的方法.
课时教学设计案例
环节三:操作确认,探究判定定理
设计意图:引导学生有条理地进行探究,通过实践操作提出较为简便的直线和平面垂直的判定定理的猜想;结合判定定理的发现过程,可以使学生进一步体会直线与平面垂直向直线与直线垂直的转化,感受直观感知、操作确认、归纳猜想的研究立体几何的一般过程,发展直观想象核心素养.
课时教学设计案例
环节三:操作确认,探究判定定理
直线和平面垂直的判定定理:
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
符号表示:
直线与直线垂直
直线与平面垂直
设计意图:实现图形语言、文字语言、符号语言之间的转换,方便学生进一步理解判定定理,同时发展逻辑思维能力.
课时教学设计案例
环节四:推理论证,定理应用
思考辨析:
(1)为什么一条直线和一个平面内的两条相交直线都垂直时,这条直线就和这个平面垂直?尝试从基底的角度去解释下原因.
(2)由推论3可知,两平行直线也可以确定一个平面,那么定理中的“两条相交直线”可以改为“两条平行直线”吗?
设计意图:设置思考对判定定理进行解释与辨析,促使学生确认此定理的正确性并加深对“两条相交直线”这一关键条件的认识.
课时教学设计案例
环节四:推理论证,定理应用
求证:如果两条平行直线中的一条直线垂直于一个平面,那么另一条直线也垂直于这个平面.
在平面内任取一条直线,利用定义去证明亦可.
设计意图:教师板书示范,再次强调三种语言的转换;同时通过例题巩固判定定理并结合例题让学生把握两条相交直线这一关键条件;通过引导学生从定义出发进行证明,进而提高思维的灵活性,促使学生认识到证明线面垂直一般有两种方法——借助定义直接证明和利用判定定理证明.
课时教学设计案例
环节四:推理论证,定理应用
设计意图:巩固练习,学生独立完成,体会判定定理.
课时教学设计案例
环节五:课堂小结,课后作业
1.这节课我们学习了哪些知识?
直线与平面垂直的定义和判定定理.
2.在学习的过程中采用了哪些方法?体现了什么数学思想?
结合生活直观感知,动手实验操作确认,得出猜想归纳总结,思考辨析推理论证.
在这过程中我们把空间问题转化成了平面问题,把无限问题转化成了有限问题,体现了转化思想.
设计意图:通过小结1,2梳理本节课所学的知识,并回顾本节课的学习过程,进一步体会立体几何的研究路径和方法;通过小结3实现单元教学知识的系统化、结构化;布置课后作业以巩固提升,有余力的同学可继续深入探究.
3.类比平行的研究路径,下节课将学习什么内容?
课后作业:课本152页第1、3、4题;探究如何证明判定定理(选做).
课时教学设计案例
板书设计
THANK YOU FOR WATCHING
谢谢各位专家!
8.6.2 直线与平面垂直(第1课时)
“整章-单元-课时”说课
目录
CONTENTS
01
整章分析
02
单元内容及其解析
03
单元目标及其解析
04
单元教学问题诊断分析
05
单元教学条件支持分析
06
课时教学设计
01
整章分析
立体几何大单元知识框架:
直线、平面的垂直
形状
可视化
大小
位置关系
02
单元内容及其解析
直线、平面的垂直
知识的
上下位关系
内容本质
蕴含的数学思想
和方法
育人价值
教学重点
单元内容及其解析
内容
单元内容及其解析
内容:本单元包括直线与直线垂直、直线与平面垂直、平面与平面垂直.
以下为单元知识框图:
单元内容及其解析
内容本质
蕴含的数学思想与方法
知识的上下位关系
育人价值
教学重点
单元内容及其解析
内容本质
蕴含的数学思想与方法
知识的上下位关系
育人价值
教学重点
单元内容及其解析
内容本质
蕴含的数学思想与方法
知识的上下位关系
育人价值
教学重点
本单元是立体几何初步最后一单元,上承空间中的平行关系.学完本单元后可以初步建立起立体几何的完整体系,也为后续在选择性必修中用空间向量研究立体几何打下基础.
单元内容及其解析
内容本质
蕴含的数学思想与方法
知识的上下位关系
育人价值
教学重点
单元内容及其解析
内容本质
蕴含的数学思想与方法
知识的上下位关系
育人价值
教学重点
03
单元目标及其解析
单元目标及其解析:
04
单元教学问题诊断分析
单元教学问题诊断分析:
05
单元教学支持条件分析
生活实例、图片
GeoGebra软件
模型、三角形纸片等工具
智慧课堂等
教学支持条件
教学支持条件分析:
通过观察和展示现实生活中的实例与图片,可以很大程度促进学生直观感知直线、平面垂直的形象;
准备模型、三角形纸片等工具,用于探究定理;
利用GeoGebra软件或制作多媒体课件动态演示,加深对空间垂直关系的感知与理解
06
课时教学设计
课时教学设计案例
8.6.2 直线与平面垂直(第1课时)
课时教学设计案例
课时教学内容:直线与平面垂直的概念、判定定理
课时教学目标:(1)理解直线与平面垂直的意义、点到平面的距离;
(2)探索并了解直线与平面垂直的判定定理,能利用判定定理证明直线与平面垂直的简单问题;
(3)在探索直线与平面垂直判定定理的过程中发展合情推理能力、感悟和体验“空间问题转化为平面问题”“线面垂直转化为线线垂直”,进一步感悟数学中“以简驭繁”的转化思想.
课时教学内容
课时教学目标
教学重点
教学难点
教学过程设计
课时教学设计案例
教学重点:直线与平面垂直定义的抽象与归纳,以及直线与平面垂直判定定理的发现与验证.
教学难点:发现并验证直线与平面垂直的判定定理.
课时教学内容
课时教学目标
教学重点
教学难点
教学过程设计
课时教学设计案例
教学过程:五个环节
环节一:微课引入,单元框架
环节二:直观感知,归纳定义
环节三:操作确认,探究判定定理
环节四:推理论证,定理简单应用
环节五:课堂小结,课后作业
课时教学内容
课时教学目标
教学重点
教学难点
教学过程设计
课时教学设计案例
环节一:微课引入,单元框架
课时教学设计案例
环节一:微课引入,单元框架
问题1:类比平行的研究思路,接下来我们应该研究什么?
设计意图:借助微课梳理本章知识结构,同时回顾平行的研究思路,通过类比提出问题,明确本节课的研究内容和路径.
课时教学设计案例
旗杆与地面的位置关系
桥柱与水面的位置关系
设计意图:通过大量生活实例和图片加深学生对直线与平面垂直的感性认识,为后续引入用数学语言刻画生活中的直线与平面垂直做铺垫.
问题2:结合生活,请举出可以抽象成直线与平面垂直的具体实例.
环节二:直观感知,归纳定义
课时教学设计案例
环节二:直观感知,归纳定义
问题3:能否把直线与平面垂直的直观形象数学化,用明确的数学语言给出定义呢?结合旗杆例子进行探究.
思考1:阳光下,直立于地面的旗杆及它在地面的影子有何位置关系
思考2:随着太阳的移动,旗杆及它在地面的影子位置关系又是什么呢?
A
B
α
思考3:旗杆与地面上任意一条不过B点的直线位置关系又如何?
设计意图:为了用明确的数学语言下定义,借助三个思考进行突破.其中思考1和思考2说明了旗杆和平面内任意相交的直线垂直,思考3则说明了旗杆与平面内任意异面直线垂直.通过观察与思考把直观模糊的感性认识抽象化、确切化,顺势引导学生归纳概括出直线与平面垂直的定义.
B1
C1
C
B
课时教学设计案例
环节二:直观感知,归纳定义
直线与平面垂直的定义:
如果直线l 与平面α内的任意一条直线都垂直,我们就说直线l 与平面α互相垂直. 记作l⊥α
l
平面α的垂线
直线l 的垂面
A
垂足
课时教学设计案例
环节二:直观感知,归纳定义
(1)如果一条直线与一个平面垂直,那么这条直线与平面内任意一条直线都垂直.
(2)如果一条直线与一个平面垂直,那么这条直线与平面内无数条直线都垂直.
(3)如果一条直线与一个平面内的一条直线不垂直,那么这条直线与这个平面不垂直.
(4)过一点垂直于已知平面的直线有且只有一条.
过一点作垂直于已知平面的直线,则该点与垂足间的线段,叫做这个点到该平面的垂线段,垂线段的长度叫做点到该平面的距离.
设计意图:加深概念理解,掌握定义本质,明确任意一条与无数条的区别;通过判断(4)让学生直观感知该结论,进而给出垂线段、点到平面的距离的概念,顺势介绍棱锥的高的概念,从而实现了感性认识到理性认知的转变,弥补了结构特征单元中的概念不足.
课时教学设计案例
环节三:操作确认,探究判定定理
动手操作:
请同学们准备一块三角形的纸片,我们一起来做如图所示的试验:过△ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD、DC与桌面接触).
A
B
C
D
思考:(1)折痕AD与桌面垂直吗?
(2)如何翻折才能保证折痕AD与桌面所在平面α垂直?
设计意图:根据定义,判断直线与平面垂直,需要验证直线与平面内的所有直线都垂直,这是一个无限问题,难以操作.类比平面与平面平行的判定定理,需要寻求判定直线与平面垂直的简单、易行的方法.
课时教学设计案例
环节三:操作确认,探究判定定理
设计意图:引导学生有条理地进行探究,通过实践操作提出较为简便的直线和平面垂直的判定定理的猜想;结合判定定理的发现过程,可以使学生进一步体会直线与平面垂直向直线与直线垂直的转化,感受直观感知、操作确认、归纳猜想的研究立体几何的一般过程,发展直观想象核心素养.
课时教学设计案例
环节三:操作确认,探究判定定理
直线和平面垂直的判定定理:
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
符号表示:
直线与直线垂直
直线与平面垂直
设计意图:实现图形语言、文字语言、符号语言之间的转换,方便学生进一步理解判定定理,同时发展逻辑思维能力.
课时教学设计案例
环节四:推理论证,定理应用
思考辨析:
(1)为什么一条直线和一个平面内的两条相交直线都垂直时,这条直线就和这个平面垂直?尝试从基底的角度去解释下原因.
(2)由推论3可知,两平行直线也可以确定一个平面,那么定理中的“两条相交直线”可以改为“两条平行直线”吗?
设计意图:设置思考对判定定理进行解释与辨析,促使学生确认此定理的正确性并加深对“两条相交直线”这一关键条件的认识.
课时教学设计案例
环节四:推理论证,定理应用
求证:如果两条平行直线中的一条直线垂直于一个平面,那么另一条直线也垂直于这个平面.
在平面内任取一条直线,利用定义去证明亦可.
设计意图:教师板书示范,再次强调三种语言的转换;同时通过例题巩固判定定理并结合例题让学生把握两条相交直线这一关键条件;通过引导学生从定义出发进行证明,进而提高思维的灵活性,促使学生认识到证明线面垂直一般有两种方法——借助定义直接证明和利用判定定理证明.
课时教学设计案例
环节四:推理论证,定理应用
设计意图:巩固练习,学生独立完成,体会判定定理.
课时教学设计案例
环节五:课堂小结,课后作业
1.这节课我们学习了哪些知识?
直线与平面垂直的定义和判定定理.
2.在学习的过程中采用了哪些方法?体现了什么数学思想?
结合生活直观感知,动手实验操作确认,得出猜想归纳总结,思考辨析推理论证.
在这过程中我们把空间问题转化成了平面问题,把无限问题转化成了有限问题,体现了转化思想.
设计意图:通过小结1,2梳理本节课所学的知识,并回顾本节课的学习过程,进一步体会立体几何的研究路径和方法;通过小结3实现单元教学知识的系统化、结构化;布置课后作业以巩固提升,有余力的同学可继续深入探究.
3.类比平行的研究路径,下节课将学习什么内容?
课后作业:课本152页第1、3、4题;探究如何证明判定定理(选做).
课时教学设计案例
板书设计
THANK YOU FOR WATCHING
谢谢各位专家!
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
