湘教版七年级数学下册 名校优选精练 第一章检测题【含答案】
文档属性
| 名称 | 湘教版七年级数学下册 名校优选精练 第一章检测题【含答案】 |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-15 22:03:14 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
湘教版七年级数学下册 名校优选精练 第一章检测题
(时间:120分钟,满分:120分)
班级: 姓名: 成绩: .
一、选择题(每小题3分,共36分)
1.下列方程组中,不是二元一次方程组的是 ( )
A. B.
C. D.
2.用加减消元法解方程组时,有下列四种变形,正确的是( )
A. B.
C. D.
3.方程2x+y=8的正整数解的组数是( )
A.4组 B.3组 C.2组 D.1组
4.根据下面所给信息,则每只玩具小猫的价格为( )
买一共要70元,买一共要50元.
A.10元 B.30元 C.40元 D.50元
5.已知是二元一次方程组的解,则m-n的值是 ( )
A.1 B.2 C.3 D.4
6.已知代数式-3xm-1y3与xnym+n是同类项,那么m、n的值分别为 ( )
A. B.
C. D.
7.在等式y=kx+b中,当x=1时,y=2;当x=2时,y=5,则k、b的值为 ( )
A. B.
C. D.
8.已知是方程组的解,则a与b的关系是( )
A.4b-9a=1 B.9a+4b=7
C.3a+2b=3 D.4b-9a=-1
9.三元一次方程组的解是( )
A. B. C. D.
10.一个两位数的十位数字与个位数字的和是8,把这个两位数加上18,结果恰好成为数字对调后组成的两位数,求这个两位数.设个位数字为x,十位数字为y,所列方程组正确的是( )
A. B.
C. D.
11.足球比赛的记分规则是:胜一场记3分,平一场记1分,负一场记0分.一支中学生足球队参加了15场比赛,负了4场,共得29分,则这支球队胜了 ( )
A.5场 B.7场 C.9场 D.11场
12.为了改善住房条件,小亮的父母考察了某小区的A、B两套楼房,A套楼房在第3层楼,B套楼房在第5层楼,B套楼房的面积比A套楼房的面积大24 m2,两套楼房的总房价相同,第3层楼和第5层楼每平方米的价格分别是平均价格的1.1倍和0.9倍,为了计算两套楼房的面积,小亮设A套楼房的面积为x m2,B套楼房的面积为y m2,根据以上信息得出了下列方程组,其中正确的是 ( )
A. B.
C. D.
二、填空题(每小题3分,共18分)
13.已知二元一次方程3x+2y=6,用含x的代数式表示y,则y=,任意写出方程的两组解为 .
14.已知则(x+y)(x-y)= (用a,b表示).
15.已知x+2y=3-m,且2x+y=-m+4,则x-y的值是 .
16.若|3a+4b-c|+(c-2b)2=0,则a∶b∶c= .
17.某银行现有定期和活期存款共4 600万元,与去年同期相比,定期存款增加了25%,活期存款减少了25%,存款总额增加了15%,去年同期有定期存款 万元,活期存款 万元.
18.某校现有校舍20 000平方米,计划拆部分旧校舍,建新校舍,且新建校舍的面积比拆除的面积的4倍多2 000平方米,如要使建设后校舍总面积比现有总面积多40%,则要拆除 平方米旧的校舍,新建 平方米校舍.
三、解答题(共66分)
19.(12分)解方程组.
(1)
(2)
(3)
20.(6分)(贺州中考)已知关于x,y的方程组的解为求m,n的值.
21.(6分)已知方程组的解中x的值为正整数,求整数a的值.
22.(7分)若方程组的解为求ba的值.
23.(8分)2021年北京市生产运营用水和居民家庭用水的总和为5.8亿立方米,其中居民家庭用水比生产运营用水的3倍还多0.6亿立方米,问生产运营用水和居民家庭用水各多少亿立方米?
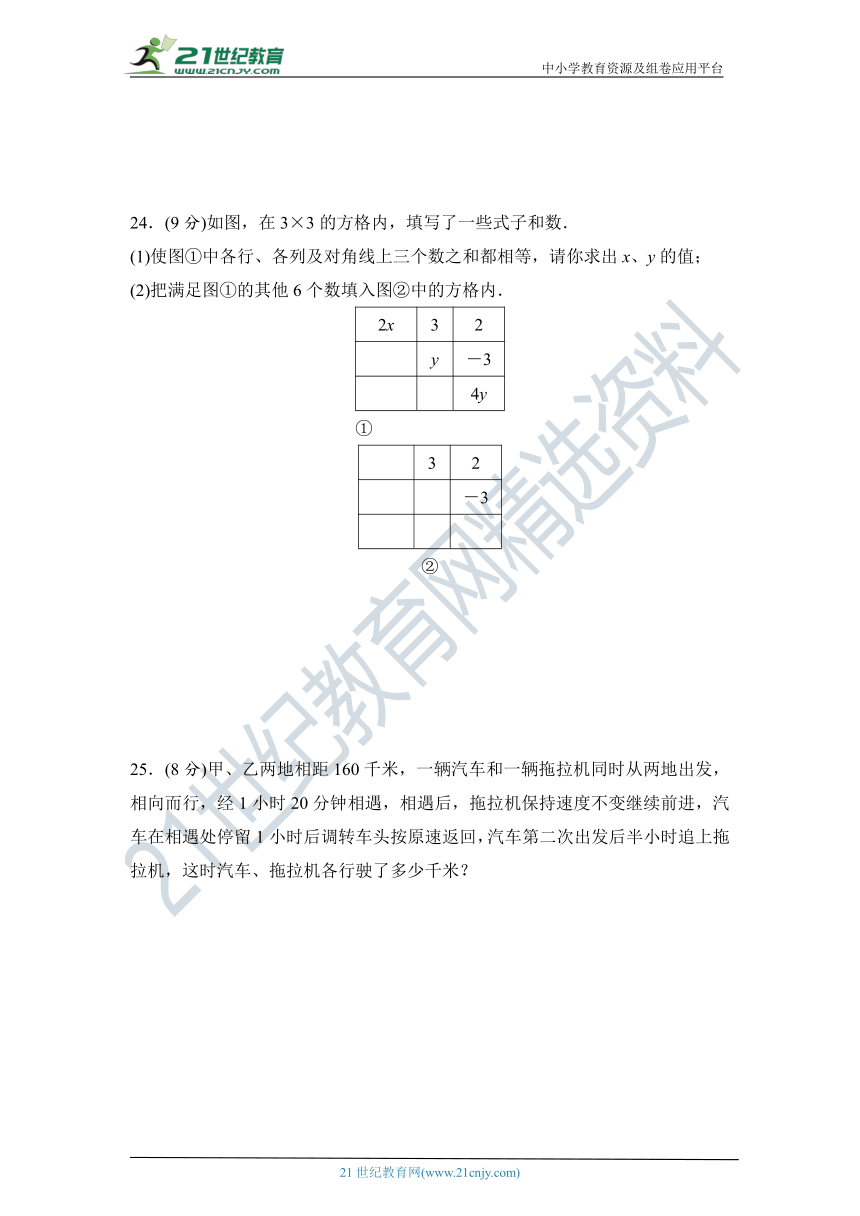
24.(9分)如图,在3×3的方格内,填写了一些式子和数.
(1)使图①中各行、各列及对角线上三个数之和都相等,请你求出x、y的值;
(2)把满足图①的其他6个数填入图②中的方格内.
2x 3 2
y -3
4y
①
3 2
-3
②
25.(8分)甲、乙两地相距160千米,一辆汽车和一辆拖拉机同时从两地出发,相向而行,经1小时20分钟相遇,相遇后,拖拉机保持速度不变继续前进,汽车在相遇处停留1小时后调转车头按原速返回,汽车第二次出发后半小时追上拖拉机,这时汽车、拖拉机各行驶了多少千米?
26.(10分)某纸品厂要制作如图所示的甲、乙两种无盖的长方体小盒,该厂利用边角材料裁出了长方形和正方形的两种纸片,其中长方形纸片的宽与正方形纸片的边长相等,现将150张正方形纸片和300张长方形纸片用来制作这两种小盒(不计连接部分),可以做成甲、乙两种小盒各多少个?
(1)设可做成甲种小盒x个,乙种小盒y个,如何列方程组求解?
(2)设做甲种小盒要用去x张长方形纸片,做乙种小盒要用去y张长方形纸片,如何列方程组求解?
参考答案
一、选择题(每小题3分,共36分)
1.下列方程组中,不是二元一次方程组的是 (B)
A. B.
C. D.
2.用加减消元法解方程组时,有下列四种变形,正确的是 (C)
A. B.
C. D.
3.方程2x+y=8的正整数解的组数是 (B)
A.4组 B.3组 C.2组 D.1组
4.根据下面所给信息,则每只玩具小猫的价格为 (A)
买一共要70元,买一共要50元.
A.10元 B.30元 C.40元 D.50元
5.已知是二元一次方程组的解,则m-n的值是(D)
A.1 B.2 C.3 D.4
6.已知代数式-3xm-1y3与xnym+n是同类项,那么m、n的值分别为(C)
A. B.
C. D.
7.在等式y=kx+b中,当x=1时,y=2;当x=2时,y=5,则k、b的值为(C)
A. B.
C. D.
8.已知是方程组的解,则a与b的关系是(B)
A.4b-9a=1 B.9a+4b=7
C.3a+2b=3 D.4b-9a=-1
9.三元一次方程组的解是 (C)
A. B. C. D.
10.一个两位数的十位数字与个位数字的和是8,把这个两位数加上18,结果恰好成为数字对调后组成的两位数,求这个两位数.设个位数字为x,十位数字为y,所列方程组正确的是 (B)
A. B.
C. D.
11.足球比赛的记分规则是:胜一场记3分,平一场记1分,负一场记0分.一支中学生足球队参加了15场比赛,负了4场,共得29分,则这支球队胜了(C)
A.5场 B.7场 C.9场 D.11场
12.为了改善住房条件,小亮的父母考察了某小区的A、B两套楼房,A套楼房在第3层楼,B套楼房在第5层楼,B套楼房的面积比A套楼房的面积大24 m2,两套楼房的总房价相同,第3层楼和第5层楼每平方米的价格分别是平均价格的1.1倍和0.9倍,为了计算两套楼房的面积,小亮设A套楼房的面积为x m2,B套楼房的面积为y m2,根据以上信息得出了下列方程组,其中正确的是(D)
A. B.
C. D.
二、填空题(每小题3分,共18分)
13.已知二元一次方程3x+2y=6,用含x的代数式表示y,则y=,任意写出方程的两组解为____.
14.已知则(x+y)(x-y)=__a2-b2__(用a,b表示).
15.已知x+2y=3-m,且2x+y=-m+4,则x-y的值是__1__.
16.若|3a+4b-c|+(c-2b)2=0,则a∶b∶c=__-2∶3∶6__.
17.某银行现有定期和活期存款共4 600万元,与去年同期相比,定期存款增加了25%,活期存款减少了25%,存款总额增加了15%,去年同期有定期存款__3_200__万元,活期存款__800__万元.
18.某校现有校舍20 000平方米,计划拆部分旧校舍,建新校舍,且新建校舍的面积比拆除的面积的4倍多2 000平方米,如要使建设后校舍总面积比现有总面积多40%,则要拆除__2_000__平方米旧的校舍,新建__10_000__平方米校舍.
三、解答题(共66分)
19.(12分)解方程组.
(1)
解:②-①×2,得7y=-5
∴y=-.
把y=-代入①,得x=.
∴
(2)
解:整理得:
③-④×5 46y=46
∴y=1.
把y=1代入③得x=7.
∴
(3)
解:①+②,得:3x+4y=24 ④
②+③,得:6x-3y=15 ⑤
④,⑤组成方程组
解得:把代入②得
z=8,∴
20.(6分)(贺州中考)已知关于x,y的方程组的解为求m,n的值.
解:将代入得
②-①,得n=,n=1.
把n=1代入②,得m=1.
所以m=1,n=1.
21.(6分)已知方程组的解中x的值为正整数,求整数a的值.
解:由方程组可解得x=,因为x为正整数,a为整数,所以2a+3只能为1或11,所以a=-1或4.
22.(7分)若方程组的解为求ba的值.
解:所以ba=(-2)1=-2.
23.(8分)2021年北京市生产运营用水和居民家庭用水的总和为5.8亿立方米,其中居民家庭用水比生产运营用水的3倍还多0.6亿立方米,问生产运营用水和居民家庭用水各多少亿立方米?
解:设生产运营用水x亿立方米,居民家庭用水y亿立方米,依题意得解得
答:生产运营用水1.3亿立方米,居民家庭用水4.5亿立方米.
24.(9分)如图,在3×3的方格内,填写了一些式子和数.
(1)使图①中各行、各列及对角线上三个数之和都相等,请你求出x、y的值;
(2)把满足图①的其他6个数填入图②中的方格内.
2x 3 2
y -3
4y
①
3 2
-3
②
解:(1)由已知,得解得
(2)由(1)可得如图所示的表:
-2 3 2
5 1 -3
0 -1 4
25.(8分)甲、乙两地相距160千米,一辆汽车和一辆拖拉机同时从两地出发,相向而行,经1小时20分钟相遇,相遇后,拖拉机保持速度不变继续前进,汽车在相遇处停留1小时后调转车头按原速返回,汽车第二次出发后半小时追上拖拉机,这时汽车、拖拉机各行驶了多少千米?
解:设汽车的速度为x千米/时,拖拉机的速度为y千米/时,
根据题意,得
解这个方程组,得经检验,符合题意,
所以汽车:90×(+)=165(千米),
拖拉机:30×(+1+)=85(千米).
26.(10分)某纸品厂要制作如图所示的甲、乙两种无盖的长方体小盒,该厂利用边角材料裁出了长方形和正方形的两种纸片,其中长方形纸片的宽与正方形纸片的边长相等,现将150张正方形纸片和300张长方形纸片用来制作这两种小盒(不计连接部分),可以做成甲、乙两种小盒各多少个?
(1)设可做成甲种小盒x个,乙种小盒y个,如何列方程组求解?
(2)设做甲种小盒要用去x张长方形纸片,做乙种小盒要用去y张长方形纸片,如何列方程组求解?
解:(1)解得
(2)解得
从而=30,=60.则做甲种小盒30个,做乙种小盒60个.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
湘教版七年级数学下册 名校优选精练 第一章检测题
(时间:120分钟,满分:120分)
班级: 姓名: 成绩: .
一、选择题(每小题3分,共36分)
1.下列方程组中,不是二元一次方程组的是 ( )
A. B.
C. D.
2.用加减消元法解方程组时,有下列四种变形,正确的是( )
A. B.
C. D.
3.方程2x+y=8的正整数解的组数是( )
A.4组 B.3组 C.2组 D.1组
4.根据下面所给信息,则每只玩具小猫的价格为( )
买一共要70元,买一共要50元.
A.10元 B.30元 C.40元 D.50元
5.已知是二元一次方程组的解,则m-n的值是 ( )
A.1 B.2 C.3 D.4
6.已知代数式-3xm-1y3与xnym+n是同类项,那么m、n的值分别为 ( )
A. B.
C. D.
7.在等式y=kx+b中,当x=1时,y=2;当x=2时,y=5,则k、b的值为 ( )
A. B.
C. D.
8.已知是方程组的解,则a与b的关系是( )
A.4b-9a=1 B.9a+4b=7
C.3a+2b=3 D.4b-9a=-1
9.三元一次方程组的解是( )
A. B. C. D.
10.一个两位数的十位数字与个位数字的和是8,把这个两位数加上18,结果恰好成为数字对调后组成的两位数,求这个两位数.设个位数字为x,十位数字为y,所列方程组正确的是( )
A. B.
C. D.
11.足球比赛的记分规则是:胜一场记3分,平一场记1分,负一场记0分.一支中学生足球队参加了15场比赛,负了4场,共得29分,则这支球队胜了 ( )
A.5场 B.7场 C.9场 D.11场
12.为了改善住房条件,小亮的父母考察了某小区的A、B两套楼房,A套楼房在第3层楼,B套楼房在第5层楼,B套楼房的面积比A套楼房的面积大24 m2,两套楼房的总房价相同,第3层楼和第5层楼每平方米的价格分别是平均价格的1.1倍和0.9倍,为了计算两套楼房的面积,小亮设A套楼房的面积为x m2,B套楼房的面积为y m2,根据以上信息得出了下列方程组,其中正确的是 ( )
A. B.
C. D.
二、填空题(每小题3分,共18分)
13.已知二元一次方程3x+2y=6,用含x的代数式表示y,则y=,任意写出方程的两组解为 .
14.已知则(x+y)(x-y)= (用a,b表示).
15.已知x+2y=3-m,且2x+y=-m+4,则x-y的值是 .
16.若|3a+4b-c|+(c-2b)2=0,则a∶b∶c= .
17.某银行现有定期和活期存款共4 600万元,与去年同期相比,定期存款增加了25%,活期存款减少了25%,存款总额增加了15%,去年同期有定期存款 万元,活期存款 万元.
18.某校现有校舍20 000平方米,计划拆部分旧校舍,建新校舍,且新建校舍的面积比拆除的面积的4倍多2 000平方米,如要使建设后校舍总面积比现有总面积多40%,则要拆除 平方米旧的校舍,新建 平方米校舍.
三、解答题(共66分)
19.(12分)解方程组.
(1)
(2)
(3)
20.(6分)(贺州中考)已知关于x,y的方程组的解为求m,n的值.
21.(6分)已知方程组的解中x的值为正整数,求整数a的值.
22.(7分)若方程组的解为求ba的值.
23.(8分)2021年北京市生产运营用水和居民家庭用水的总和为5.8亿立方米,其中居民家庭用水比生产运营用水的3倍还多0.6亿立方米,问生产运营用水和居民家庭用水各多少亿立方米?
24.(9分)如图,在3×3的方格内,填写了一些式子和数.
(1)使图①中各行、各列及对角线上三个数之和都相等,请你求出x、y的值;
(2)把满足图①的其他6个数填入图②中的方格内.
2x 3 2
y -3
4y
①
3 2
-3
②
25.(8分)甲、乙两地相距160千米,一辆汽车和一辆拖拉机同时从两地出发,相向而行,经1小时20分钟相遇,相遇后,拖拉机保持速度不变继续前进,汽车在相遇处停留1小时后调转车头按原速返回,汽车第二次出发后半小时追上拖拉机,这时汽车、拖拉机各行驶了多少千米?
26.(10分)某纸品厂要制作如图所示的甲、乙两种无盖的长方体小盒,该厂利用边角材料裁出了长方形和正方形的两种纸片,其中长方形纸片的宽与正方形纸片的边长相等,现将150张正方形纸片和300张长方形纸片用来制作这两种小盒(不计连接部分),可以做成甲、乙两种小盒各多少个?
(1)设可做成甲种小盒x个,乙种小盒y个,如何列方程组求解?
(2)设做甲种小盒要用去x张长方形纸片,做乙种小盒要用去y张长方形纸片,如何列方程组求解?
参考答案
一、选择题(每小题3分,共36分)
1.下列方程组中,不是二元一次方程组的是 (B)
A. B.
C. D.
2.用加减消元法解方程组时,有下列四种变形,正确的是 (C)
A. B.
C. D.
3.方程2x+y=8的正整数解的组数是 (B)
A.4组 B.3组 C.2组 D.1组
4.根据下面所给信息,则每只玩具小猫的价格为 (A)
买一共要70元,买一共要50元.
A.10元 B.30元 C.40元 D.50元
5.已知是二元一次方程组的解,则m-n的值是(D)
A.1 B.2 C.3 D.4
6.已知代数式-3xm-1y3与xnym+n是同类项,那么m、n的值分别为(C)
A. B.
C. D.
7.在等式y=kx+b中,当x=1时,y=2;当x=2时,y=5,则k、b的值为(C)
A. B.
C. D.
8.已知是方程组的解,则a与b的关系是(B)
A.4b-9a=1 B.9a+4b=7
C.3a+2b=3 D.4b-9a=-1
9.三元一次方程组的解是 (C)
A. B. C. D.
10.一个两位数的十位数字与个位数字的和是8,把这个两位数加上18,结果恰好成为数字对调后组成的两位数,求这个两位数.设个位数字为x,十位数字为y,所列方程组正确的是 (B)
A. B.
C. D.
11.足球比赛的记分规则是:胜一场记3分,平一场记1分,负一场记0分.一支中学生足球队参加了15场比赛,负了4场,共得29分,则这支球队胜了(C)
A.5场 B.7场 C.9场 D.11场
12.为了改善住房条件,小亮的父母考察了某小区的A、B两套楼房,A套楼房在第3层楼,B套楼房在第5层楼,B套楼房的面积比A套楼房的面积大24 m2,两套楼房的总房价相同,第3层楼和第5层楼每平方米的价格分别是平均价格的1.1倍和0.9倍,为了计算两套楼房的面积,小亮设A套楼房的面积为x m2,B套楼房的面积为y m2,根据以上信息得出了下列方程组,其中正确的是(D)
A. B.
C. D.
二、填空题(每小题3分,共18分)
13.已知二元一次方程3x+2y=6,用含x的代数式表示y,则y=,任意写出方程的两组解为____.
14.已知则(x+y)(x-y)=__a2-b2__(用a,b表示).
15.已知x+2y=3-m,且2x+y=-m+4,则x-y的值是__1__.
16.若|3a+4b-c|+(c-2b)2=0,则a∶b∶c=__-2∶3∶6__.
17.某银行现有定期和活期存款共4 600万元,与去年同期相比,定期存款增加了25%,活期存款减少了25%,存款总额增加了15%,去年同期有定期存款__3_200__万元,活期存款__800__万元.
18.某校现有校舍20 000平方米,计划拆部分旧校舍,建新校舍,且新建校舍的面积比拆除的面积的4倍多2 000平方米,如要使建设后校舍总面积比现有总面积多40%,则要拆除__2_000__平方米旧的校舍,新建__10_000__平方米校舍.
三、解答题(共66分)
19.(12分)解方程组.
(1)
解:②-①×2,得7y=-5
∴y=-.
把y=-代入①,得x=.
∴
(2)
解:整理得:
③-④×5 46y=46
∴y=1.
把y=1代入③得x=7.
∴
(3)
解:①+②,得:3x+4y=24 ④
②+③,得:6x-3y=15 ⑤
④,⑤组成方程组
解得:把代入②得
z=8,∴
20.(6分)(贺州中考)已知关于x,y的方程组的解为求m,n的值.
解:将代入得
②-①,得n=,n=1.
把n=1代入②,得m=1.
所以m=1,n=1.
21.(6分)已知方程组的解中x的值为正整数,求整数a的值.
解:由方程组可解得x=,因为x为正整数,a为整数,所以2a+3只能为1或11,所以a=-1或4.
22.(7分)若方程组的解为求ba的值.
解:所以ba=(-2)1=-2.
23.(8分)2021年北京市生产运营用水和居民家庭用水的总和为5.8亿立方米,其中居民家庭用水比生产运营用水的3倍还多0.6亿立方米,问生产运营用水和居民家庭用水各多少亿立方米?
解:设生产运营用水x亿立方米,居民家庭用水y亿立方米,依题意得解得
答:生产运营用水1.3亿立方米,居民家庭用水4.5亿立方米.
24.(9分)如图,在3×3的方格内,填写了一些式子和数.
(1)使图①中各行、各列及对角线上三个数之和都相等,请你求出x、y的值;
(2)把满足图①的其他6个数填入图②中的方格内.
2x 3 2
y -3
4y
①
3 2
-3
②
解:(1)由已知,得解得
(2)由(1)可得如图所示的表:
-2 3 2
5 1 -3
0 -1 4
25.(8分)甲、乙两地相距160千米,一辆汽车和一辆拖拉机同时从两地出发,相向而行,经1小时20分钟相遇,相遇后,拖拉机保持速度不变继续前进,汽车在相遇处停留1小时后调转车头按原速返回,汽车第二次出发后半小时追上拖拉机,这时汽车、拖拉机各行驶了多少千米?
解:设汽车的速度为x千米/时,拖拉机的速度为y千米/时,
根据题意,得
解这个方程组,得经检验,符合题意,
所以汽车:90×(+)=165(千米),
拖拉机:30×(+1+)=85(千米).
26.(10分)某纸品厂要制作如图所示的甲、乙两种无盖的长方体小盒,该厂利用边角材料裁出了长方形和正方形的两种纸片,其中长方形纸片的宽与正方形纸片的边长相等,现将150张正方形纸片和300张长方形纸片用来制作这两种小盒(不计连接部分),可以做成甲、乙两种小盒各多少个?
(1)设可做成甲种小盒x个,乙种小盒y个,如何列方程组求解?
(2)设做甲种小盒要用去x张长方形纸片,做乙种小盒要用去y张长方形纸片,如何列方程组求解?
解:(1)解得
(2)解得
从而=30,=60.则做甲种小盒30个,做乙种小盒60个.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
