湘教版七年级数学下册 名校优选精练 第四章检测题(含答案)
文档属性
| 名称 | 湘教版七年级数学下册 名校优选精练 第四章检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-15 22:05:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
湘教版七年级数学下册 名校优选精练 第四章检测题
(时间:120分钟,满分:120分)
班级: 姓名: 成绩: .
一、选择题(每小题3分,共36分)
1.如图所示,是一个镶边的模板,分析它的内部是由哪个“基本图形”通过一次平移得到的( )
2.下列说法正确的是( )
A.同位角相等 B.内错角相等
C.同旁内角相等,两直线平行 D.对顶角相等
3.如果两条平行线被第三条直线所截,则一组内错角的平分线互相( )
A.垂直 B.平行 C.重合 D.相交
4.如图,直线a、b被直线c所截,下列说法正确的是( )
A.当∠1=∠2时,一定有a∥b
B.当a∥b时,一定有∠1=∠2
C.当a∥b时,一定有∠1+∠2=90°
D.当∠1+∠2=180°时,一定有a∥b
5.4根火柴棒形成如图所示的象形“口”字,平移火柴棒后,原图形能变成的象形汉字是( )
A B C D
6.点P为直线l外一点,点A、B、C为直线l上的三点,PA=2cm,PB=3cm,PC=4cm.那么点P到直线l的距离是( )
A.2cm B.小于2cm
C.不大于2cm D.大于2cm且小于5cm
7.(邵阳中考)某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是 ( )
A.甲种方案所用铁丝最长 B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长 D.三种方案所用铁丝一样长
8.(长春中考)如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB,若∠B为锐角,BC∥DF,则∠B的大小为( )
A.30° B.45° C.60° D.75°
eq \o(\s\up7(),\s\do5(第8题图))
9.如图,一束光线垂直照射水平地面,在地面上放一个平面镜,欲使这束光线经过平面镜反射后成水平光线,则平面镜与地面所成锐角的度数为( )
A.45° B.60° C.75° D.80°
eq \o(\s\up7(),\s\do5(第9题图))
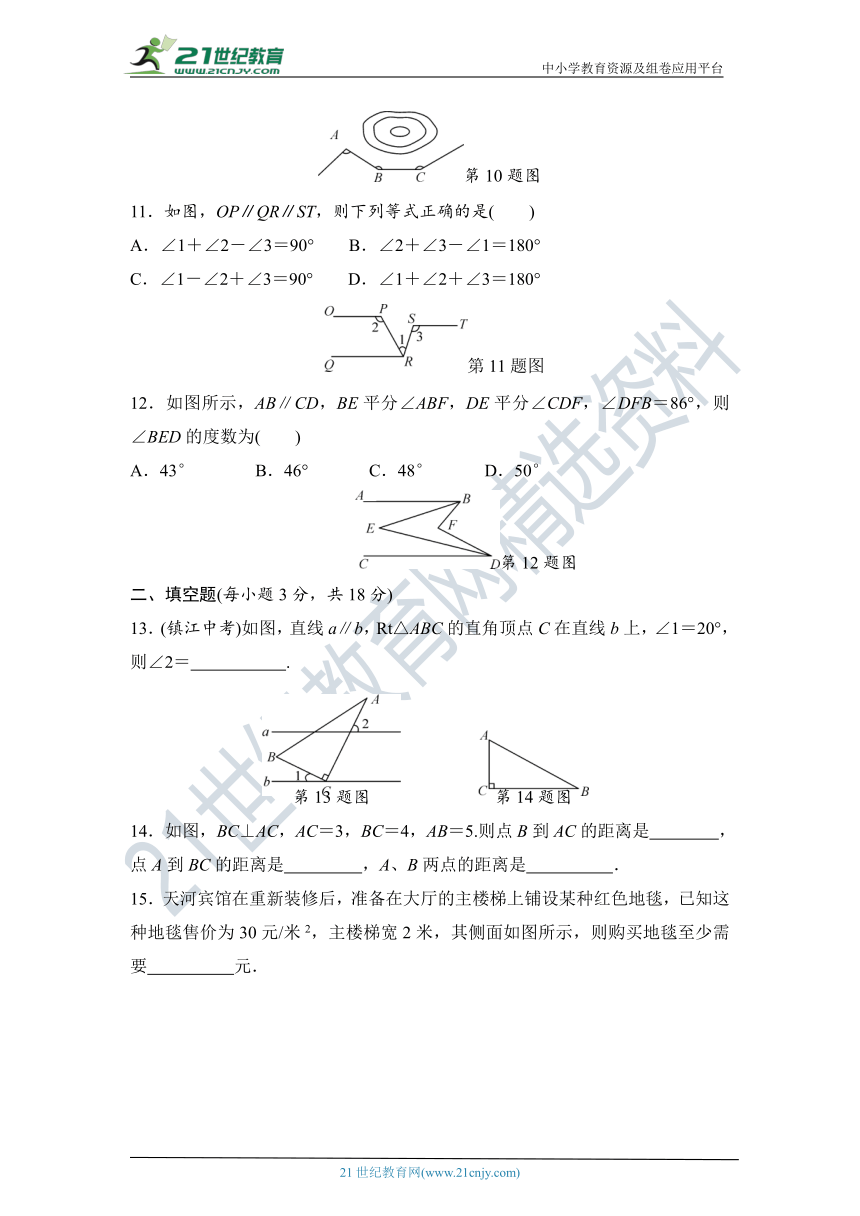
10.如图所示,一条公路修到湖边时,需要绕湖而过,如果第一次拐的角∠A=120°,第二次拐的角∠B=150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C等于( )
A.120° B.130° C.140° D.150°
第10题图
11.如图,OP∥QR∥ST,则下列等式正确的是( )
A.∠1+∠2-∠3=90° B.∠2+∠3-∠1=180°
C.∠1-∠2+∠3=90° D.∠1+∠2+∠3=180°
第11题图
12.如图所示,AB∥CD,BE平分∠ABF,DE平分∠CDF,∠DFB=86°,则∠BED的度数为( )
A.43° B.46° C.48° D.50°
第12题图
二、填空题(每小题3分,共18分)
13.(镇江中考)如图,直线a∥b,Rt△ABC的直角顶点C在直线b上,∠1=20°,则∠2= .
eq \o(\s\up7(),\s\do5(第13题图)) eq \o(\s\up7(),\s\do5(第14题图))
14.如图,BC⊥AC,AC=3,BC=4,AB=5.则点B到AC的距离是 ,点A到BC的距离是 ,A、B两点的距离是 .
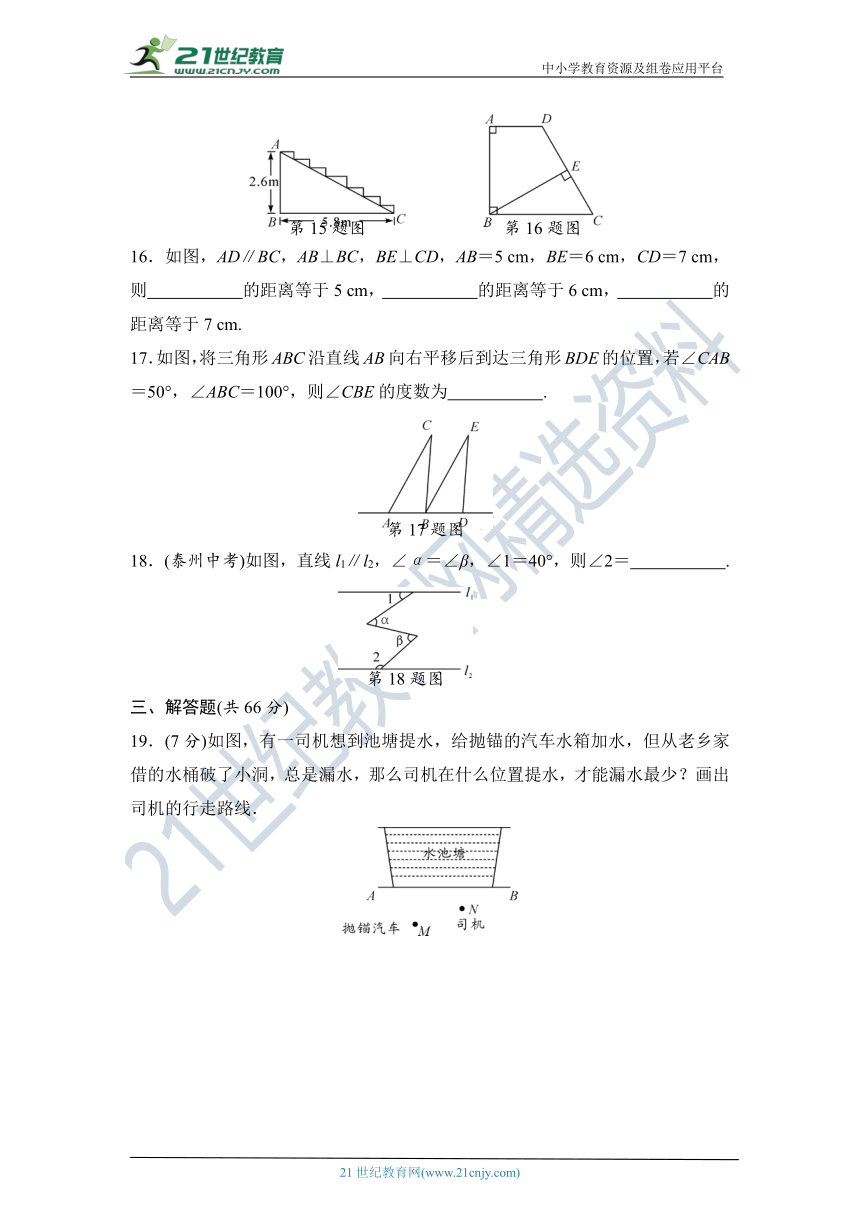
15.天河宾馆在重新装修后,准备在大厅的主楼梯上铺设某种红色地毯,已知这种地毯售价为30元/米2,主楼梯宽2米,其侧面如图所示,则购买地毯至少需要 元.
eq \o(\s\up7(),\s\do5(第15题图)) eq \o(\s\up7(),\s\do5(第16题图))
16.如图,AD∥BC,AB⊥BC,BE⊥CD,AB=5 cm,BE=6 cm,CD=7 cm,则 的距离等于5 cm, 的距离等于6 cm, 的距离等于7 cm.
17.如图,将三角形ABC沿直线AB向右平移后到达三角形BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为 .
eq \o(\s\up7(),\s\do5(第17题图))
18.(泰州中考)如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2= .
eq \o(\s\up7(),\s\do5(第18题图))
三、解答题(共66分)
19.(7分)如图,有一司机想到池塘提水,给抛锚的汽车水箱加水,但从老乡家借的水桶破了小洞,总是漏水,那么司机在什么位置提水,才能漏水最少?画出司机的行走路线.
20.(7分)如图,张三打算在院落里种上蔬菜,已知院落为东西长32 m,南北宽20 m的长方形,为了行走方便,要修筑同样宽的三条道路:东西两条,南北一条,南北道路垂直于东西道路,余下的部分要分别种上西红柿、青椒、黄瓜等蔬菜,若每条道路的宽均为1 m,求蔬菜的总种植面积是多少?
21.(8分)如图,点D、E、F分别在AB、BC、AC上,且DE∥AC,EF∥AB,下面写出了说明“∠A+∠B+∠C=180°”的过程,请填空.
∵DE∥AC,AB∥EF,
∴∠1=∠ ,∠3=∠ (两直线平行,同位角相等).
∵∠2=∠ (两直线平行,内错角相等),
且DE∥AC,
∴∠4=∠ (两直线平行,同位角相等).
∴∠2=∠A(等量代换).
∵∠1+∠2+∠3=180°,
∴∠A+∠B+∠C=180°(等量代换).
22.(8分)如图,已知AC∥DE,AD∥BE,试说明∠BAC=∠B+∠E的理由.
23.(8分)如图,在A、B两地之间要修建一条笔直的公路,从A地测得公路走向是北偏东48°,A、B两地同时开工,若干天后公路准确接通.
(1)B地所修公路的走向是南偏西多少?为什么?
(2)若公路AB长8千米,另一公路BC长6千米,且BC的走向是北偏西42°,试求A地到公路BC的距离.
24.(8分)如图,已知∠1=∠2,∠C=∠D,证明:∠A=∠F.
25.(10分)如图,直线EF,CD相交于点O,OA⊥OB,且OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?
26.(10分)已知直线l1∥l2,直线GH分别交l1、l2于A、B两点,直线MN分别交l1、l2于C、D两点,点P在直线MN上(点P和C、D不重合).
(1)如图,当点P在线段CD上时,试找出∠PAC、∠PBD、∠APB之间的关系并说出理由;
(2)当点P不在线段CD上时,试探究∠PAC、∠PBD、∠APB之间的关系(只写出结论,不说明理由).
参考答案
一、选择题(每小题3分,共36分)
1.如图所示,是一个镶边的模板,分析它的内部是由哪个“基本图形”通过一次平移得到的 (B)
2.下列说法正确的是 (D)
A.同位角相等 B.内错角相等
C.同旁内角相等,两直线平行 D.对顶角相等
3.如果两条平行线被第三条直线所截,则一组内错角的平分线互相(B)
A.垂直 B.平行 C.重合 D.相交
4.如图,直线a、b被直线c所截,下列说法正确的是 (D)
A.当∠1=∠2时,一定有a∥b
B.当a∥b时,一定有∠1=∠2
C.当a∥b时,一定有∠1+∠2=90°
D.当∠1+∠2=180°时,一定有a∥b
5.4根火柴棒形成如图所示的象形“口”字,平移火柴棒后,原图形能变成的象形汉字是 (B)
A B C D
6.点P为直线l外一点,点A、B、C为直线l上的三点,PA=2cm,PB=3cm,PC=4cm.那么点P到直线l的距离是 (C)
A.2cm B.小于2cm
C.不大于2cm D.大于2cm且小于5cm
7.(邵阳中考)某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是(D)
A.甲种方案所用铁丝最长 B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长 D.三种方案所用铁丝一样长
8.(长春中考)如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB,若∠B为锐角,BC∥DF,则∠B的大小为 (C)
A.30° B.45° C.60° D.75°
eq \o(\s\up7(),\s\do5(第8题图))
9.如图,一束光线垂直照射水平地面,在地面上放一个平面镜,欲使这束光线经过平面镜反射后成水平光线,则平面镜与地面所成锐角的度数为(A)
A.45° B.60° C.75° D.80°
eq \o(\s\up7(),\s\do5(第9题图))
10.如图所示,一条公路修到湖边时,需要绕湖而过,如果第一次拐的角∠A=120°,第二次拐的角∠B=150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C等于 (D)
A.120° B.130° C.140° D.150°
第10题图
11.如图,OP∥QR∥ST,则下列等式正确的是 (B)
A.∠1+∠2-∠3=90° B.∠2+∠3-∠1=180°
C.∠1-∠2+∠3=90° D.∠1+∠2+∠3=180°
第11题图
12.如图所示,AB∥CD,BE平分∠ABF,DE平分∠CDF,∠DFB=86°,则∠BED的度数为 (A)
A.43° B.46° C.48° D.50°
第12题图
二、填空题(每小题3分,共18分)
13.(镇江中考)如图,直线a∥b,Rt△ABC的直角顶点C在直线b上,∠1=20°,则∠2=__70__°.
eq \o(\s\up7(),\s\do5(第13题图)) eq \o(\s\up7(),\s\do5(第14题图))
14.如图,BC⊥AC,AC=3,BC=4,AB=5.则点B到AC的距离是__4__,点A到BC的距离是__3__,A、B两点的距离是__5__.
15.天河宾馆在重新装修后,准备在大厅的主楼梯上铺设某种红色地毯,已知这种地毯售价为30元/米2,主楼梯宽2米,其侧面如图所示,则购买地毯至少需要__504__元.
eq \o(\s\up7(),\s\do5(第15题图)) eq \o(\s\up7(),\s\do5(第16题图))
16.如图,AD∥BC,AB⊥BC,BE⊥CD,AB=5 cm,BE=6 cm,CD=7 cm,则__直线AD与BC之间__的距离等于5 cm,__点B到CD__的距离等于6 cm,__点C到点D__的距离等于7 cm.
17.如图,将三角形ABC沿直线AB向右平移后到达三角形BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为__30°__.
eq \o(\s\up7(),\s\do5(第17题图))
18.(泰州中考)如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=__140°__.
eq \o(\s\up7(),\s\do5(第18题图))
三、解答题(共66分)
19.(7分)如图,有一司机想到池塘提水,给抛锚的汽车水箱加水,但从老乡家借的水桶破了小洞,总是漏水,那么司机在什么位置提水,才能漏水最少?画出司机的行走路线.
解:过M点作小池塘边AB的垂线,垂足为P,连接NP,
由垂线段最短知,司机在P点处提水,才能使漏水最少,
他行走的路线是折线段NPM.
20.(7分)如图,张三打算在院落里种上蔬菜,已知院落为东西长32 m,南北宽20 m的长方形,为了行走方便,要修筑同样宽的三条道路:东西两条,南北一条,南北道路垂直于东西道路,余下的部分要分别种上西红柿、青椒、黄瓜等蔬菜,若每条道路的宽均为1 m,求蔬菜的总种植面积是多少?
解:经过平移,除去道路后,菜地长32-1=31(m),宽20-2=18(m),所以面积为31×18=558( m2).
21.(8分)如图,点D、E、F分别在AB、BC、AC上,且DE∥AC,EF∥AB,下面写出了说明“∠A+∠B+∠C=180°”的过程,请填空.
∵DE∥AC,AB∥EF,
∴∠1=∠__C__,∠3=∠__B__(两直线平行,同位角相等).
∵∠2=∠__4__(两直线平行,内错角相等),
且DE∥AC,
∴∠4=∠__A__(两直线平行,同位角相等).
∴∠2=∠A(等量代换).
∵∠1+∠2+∠3=180°,
∴∠A+∠B+∠C=180°(等量代换).
22.(8分)如图,已知AC∥DE,AD∥BE,试说明∠BAC=∠B+∠E的理由.
解:∵AC∥DE,
∴∠1=∠D.
∵AD∥BE,
∴∠2=∠B,∠D=∠E.
∴∠1=∠E.
∵∠BAC=∠1+∠2,
∴∠BAC=∠B+∠E.
23.(8分)如图,在A、B两地之间要修建一条笔直的公路,从A地测得公路走向是北偏东48°,A、B两地同时开工,若干天后公路准确接通.
(1)B地所修公路的走向是南偏西多少?为什么?
(2)若公路AB长8千米,另一公路BC长6千米,且BC的走向是北偏西42°,试求A地到公路BC的距离.
解:(1)B地所修公路的走向是南偏西48°,
理由是:两直线平行,内错角相等;
∠ABC=180°-42°-48°=90°,
故A到BC的距离为AB的长度,即8千米.
24.(8分)如图,已知∠1=∠2,∠C=∠D,证明:∠A=∠F.
证明:因为∠1=∠2,∠2=∠3,
所以∠1=∠3,所以BD∥CE.
所以∠4=∠C.
又因为∠C=∠D,
所以∠4=∠D,
所以DF∥AC,
所以∠A=∠F.
25.(10分)如图,直线EF,CD相交于点O,OA⊥OB,且OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?
解:(1)因为∠AOE+∠AOF=180°,∠AOE=40°,
所以∠AOF=140°.
又因为OC平分∠AOF,
所以∠AOC=∠AOF=70°.
因为OA⊥OB,所以∠AOB=90°.
所以∠BOD=180°-∠AOC-∠AOB=180°-70°-90°=20°.
(2)因为∠AOE+∠AOF=180°,∠AOE=α,
所以∠AOF=180°-α.
又因为OC平分∠AOF,
所以∠AOC=∠AOF=90°-α.
因为OA⊥OB,所以∠AOB=90°.
所以∠BOD=180°-∠AOC-∠AOB=180°-(90°-α)-90°=α.
(3)从(1)(2)的结果中能看出∠AOE=2∠BOD.
26.(10分)已知直线l1∥l2,直线GH分别交l1、l2于A、B两点,直线MN分别交l1、l2于C、D两点,点P在直线MN上(点P和C、D不重合).
(1)如图,当点P在线段CD上时,试找出∠PAC、∠PBD、∠APB之间的关系并说出理由;
(2)当点P不在线段CD上时,试探究∠PAC、∠PBD、∠APB之间的关系(只写出结论,不说明理由).
解:(1)∠PAC+∠PBD=∠APB.
理由如下:作PQ∥l1,交AB与点Q,则PQ∥l1∥l2.
∴∠PAC=∠APQ,∠PBD=∠BPQ.
∵∠APQ+∠BPQ=∠APB,
∴∠PAC+∠PBD=∠APB.
(2)当点P在线段DC的延长线上时,∠PAC+∠APB=∠PBD;
当点P在线段CD的延长线上时,∠PAC=∠APB+∠PBD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
湘教版七年级数学下册 名校优选精练 第四章检测题
(时间:120分钟,满分:120分)
班级: 姓名: 成绩: .
一、选择题(每小题3分,共36分)
1.如图所示,是一个镶边的模板,分析它的内部是由哪个“基本图形”通过一次平移得到的( )
2.下列说法正确的是( )
A.同位角相等 B.内错角相等
C.同旁内角相等,两直线平行 D.对顶角相等
3.如果两条平行线被第三条直线所截,则一组内错角的平分线互相( )
A.垂直 B.平行 C.重合 D.相交
4.如图,直线a、b被直线c所截,下列说法正确的是( )
A.当∠1=∠2时,一定有a∥b
B.当a∥b时,一定有∠1=∠2
C.当a∥b时,一定有∠1+∠2=90°
D.当∠1+∠2=180°时,一定有a∥b
5.4根火柴棒形成如图所示的象形“口”字,平移火柴棒后,原图形能变成的象形汉字是( )
A B C D
6.点P为直线l外一点,点A、B、C为直线l上的三点,PA=2cm,PB=3cm,PC=4cm.那么点P到直线l的距离是( )
A.2cm B.小于2cm
C.不大于2cm D.大于2cm且小于5cm
7.(邵阳中考)某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是 ( )
A.甲种方案所用铁丝最长 B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长 D.三种方案所用铁丝一样长
8.(长春中考)如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB,若∠B为锐角,BC∥DF,则∠B的大小为( )
A.30° B.45° C.60° D.75°
eq \o(\s\up7(),\s\do5(第8题图))
9.如图,一束光线垂直照射水平地面,在地面上放一个平面镜,欲使这束光线经过平面镜反射后成水平光线,则平面镜与地面所成锐角的度数为( )
A.45° B.60° C.75° D.80°
eq \o(\s\up7(),\s\do5(第9题图))
10.如图所示,一条公路修到湖边时,需要绕湖而过,如果第一次拐的角∠A=120°,第二次拐的角∠B=150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C等于( )
A.120° B.130° C.140° D.150°
第10题图
11.如图,OP∥QR∥ST,则下列等式正确的是( )
A.∠1+∠2-∠3=90° B.∠2+∠3-∠1=180°
C.∠1-∠2+∠3=90° D.∠1+∠2+∠3=180°
第11题图
12.如图所示,AB∥CD,BE平分∠ABF,DE平分∠CDF,∠DFB=86°,则∠BED的度数为( )
A.43° B.46° C.48° D.50°
第12题图
二、填空题(每小题3分,共18分)
13.(镇江中考)如图,直线a∥b,Rt△ABC的直角顶点C在直线b上,∠1=20°,则∠2= .
eq \o(\s\up7(),\s\do5(第13题图)) eq \o(\s\up7(),\s\do5(第14题图))
14.如图,BC⊥AC,AC=3,BC=4,AB=5.则点B到AC的距离是 ,点A到BC的距离是 ,A、B两点的距离是 .
15.天河宾馆在重新装修后,准备在大厅的主楼梯上铺设某种红色地毯,已知这种地毯售价为30元/米2,主楼梯宽2米,其侧面如图所示,则购买地毯至少需要 元.
eq \o(\s\up7(),\s\do5(第15题图)) eq \o(\s\up7(),\s\do5(第16题图))
16.如图,AD∥BC,AB⊥BC,BE⊥CD,AB=5 cm,BE=6 cm,CD=7 cm,则 的距离等于5 cm, 的距离等于6 cm, 的距离等于7 cm.
17.如图,将三角形ABC沿直线AB向右平移后到达三角形BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为 .
eq \o(\s\up7(),\s\do5(第17题图))
18.(泰州中考)如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2= .
eq \o(\s\up7(),\s\do5(第18题图))
三、解答题(共66分)
19.(7分)如图,有一司机想到池塘提水,给抛锚的汽车水箱加水,但从老乡家借的水桶破了小洞,总是漏水,那么司机在什么位置提水,才能漏水最少?画出司机的行走路线.
20.(7分)如图,张三打算在院落里种上蔬菜,已知院落为东西长32 m,南北宽20 m的长方形,为了行走方便,要修筑同样宽的三条道路:东西两条,南北一条,南北道路垂直于东西道路,余下的部分要分别种上西红柿、青椒、黄瓜等蔬菜,若每条道路的宽均为1 m,求蔬菜的总种植面积是多少?
21.(8分)如图,点D、E、F分别在AB、BC、AC上,且DE∥AC,EF∥AB,下面写出了说明“∠A+∠B+∠C=180°”的过程,请填空.
∵DE∥AC,AB∥EF,
∴∠1=∠ ,∠3=∠ (两直线平行,同位角相等).
∵∠2=∠ (两直线平行,内错角相等),
且DE∥AC,
∴∠4=∠ (两直线平行,同位角相等).
∴∠2=∠A(等量代换).
∵∠1+∠2+∠3=180°,
∴∠A+∠B+∠C=180°(等量代换).
22.(8分)如图,已知AC∥DE,AD∥BE,试说明∠BAC=∠B+∠E的理由.
23.(8分)如图,在A、B两地之间要修建一条笔直的公路,从A地测得公路走向是北偏东48°,A、B两地同时开工,若干天后公路准确接通.
(1)B地所修公路的走向是南偏西多少?为什么?
(2)若公路AB长8千米,另一公路BC长6千米,且BC的走向是北偏西42°,试求A地到公路BC的距离.
24.(8分)如图,已知∠1=∠2,∠C=∠D,证明:∠A=∠F.
25.(10分)如图,直线EF,CD相交于点O,OA⊥OB,且OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?
26.(10分)已知直线l1∥l2,直线GH分别交l1、l2于A、B两点,直线MN分别交l1、l2于C、D两点,点P在直线MN上(点P和C、D不重合).
(1)如图,当点P在线段CD上时,试找出∠PAC、∠PBD、∠APB之间的关系并说出理由;
(2)当点P不在线段CD上时,试探究∠PAC、∠PBD、∠APB之间的关系(只写出结论,不说明理由).
参考答案
一、选择题(每小题3分,共36分)
1.如图所示,是一个镶边的模板,分析它的内部是由哪个“基本图形”通过一次平移得到的 (B)
2.下列说法正确的是 (D)
A.同位角相等 B.内错角相等
C.同旁内角相等,两直线平行 D.对顶角相等
3.如果两条平行线被第三条直线所截,则一组内错角的平分线互相(B)
A.垂直 B.平行 C.重合 D.相交
4.如图,直线a、b被直线c所截,下列说法正确的是 (D)
A.当∠1=∠2时,一定有a∥b
B.当a∥b时,一定有∠1=∠2
C.当a∥b时,一定有∠1+∠2=90°
D.当∠1+∠2=180°时,一定有a∥b
5.4根火柴棒形成如图所示的象形“口”字,平移火柴棒后,原图形能变成的象形汉字是 (B)
A B C D
6.点P为直线l外一点,点A、B、C为直线l上的三点,PA=2cm,PB=3cm,PC=4cm.那么点P到直线l的距离是 (C)
A.2cm B.小于2cm
C.不大于2cm D.大于2cm且小于5cm
7.(邵阳中考)某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是(D)
A.甲种方案所用铁丝最长 B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长 D.三种方案所用铁丝一样长
8.(长春中考)如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB,若∠B为锐角,BC∥DF,则∠B的大小为 (C)
A.30° B.45° C.60° D.75°
eq \o(\s\up7(),\s\do5(第8题图))
9.如图,一束光线垂直照射水平地面,在地面上放一个平面镜,欲使这束光线经过平面镜反射后成水平光线,则平面镜与地面所成锐角的度数为(A)
A.45° B.60° C.75° D.80°
eq \o(\s\up7(),\s\do5(第9题图))
10.如图所示,一条公路修到湖边时,需要绕湖而过,如果第一次拐的角∠A=120°,第二次拐的角∠B=150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C等于 (D)
A.120° B.130° C.140° D.150°
第10题图
11.如图,OP∥QR∥ST,则下列等式正确的是 (B)
A.∠1+∠2-∠3=90° B.∠2+∠3-∠1=180°
C.∠1-∠2+∠3=90° D.∠1+∠2+∠3=180°
第11题图
12.如图所示,AB∥CD,BE平分∠ABF,DE平分∠CDF,∠DFB=86°,则∠BED的度数为 (A)
A.43° B.46° C.48° D.50°
第12题图
二、填空题(每小题3分,共18分)
13.(镇江中考)如图,直线a∥b,Rt△ABC的直角顶点C在直线b上,∠1=20°,则∠2=__70__°.
eq \o(\s\up7(),\s\do5(第13题图)) eq \o(\s\up7(),\s\do5(第14题图))
14.如图,BC⊥AC,AC=3,BC=4,AB=5.则点B到AC的距离是__4__,点A到BC的距离是__3__,A、B两点的距离是__5__.
15.天河宾馆在重新装修后,准备在大厅的主楼梯上铺设某种红色地毯,已知这种地毯售价为30元/米2,主楼梯宽2米,其侧面如图所示,则购买地毯至少需要__504__元.
eq \o(\s\up7(),\s\do5(第15题图)) eq \o(\s\up7(),\s\do5(第16题图))
16.如图,AD∥BC,AB⊥BC,BE⊥CD,AB=5 cm,BE=6 cm,CD=7 cm,则__直线AD与BC之间__的距离等于5 cm,__点B到CD__的距离等于6 cm,__点C到点D__的距离等于7 cm.
17.如图,将三角形ABC沿直线AB向右平移后到达三角形BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为__30°__.
eq \o(\s\up7(),\s\do5(第17题图))
18.(泰州中考)如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=__140°__.
eq \o(\s\up7(),\s\do5(第18题图))
三、解答题(共66分)
19.(7分)如图,有一司机想到池塘提水,给抛锚的汽车水箱加水,但从老乡家借的水桶破了小洞,总是漏水,那么司机在什么位置提水,才能漏水最少?画出司机的行走路线.
解:过M点作小池塘边AB的垂线,垂足为P,连接NP,
由垂线段最短知,司机在P点处提水,才能使漏水最少,
他行走的路线是折线段NPM.
20.(7分)如图,张三打算在院落里种上蔬菜,已知院落为东西长32 m,南北宽20 m的长方形,为了行走方便,要修筑同样宽的三条道路:东西两条,南北一条,南北道路垂直于东西道路,余下的部分要分别种上西红柿、青椒、黄瓜等蔬菜,若每条道路的宽均为1 m,求蔬菜的总种植面积是多少?
解:经过平移,除去道路后,菜地长32-1=31(m),宽20-2=18(m),所以面积为31×18=558( m2).
21.(8分)如图,点D、E、F分别在AB、BC、AC上,且DE∥AC,EF∥AB,下面写出了说明“∠A+∠B+∠C=180°”的过程,请填空.
∵DE∥AC,AB∥EF,
∴∠1=∠__C__,∠3=∠__B__(两直线平行,同位角相等).
∵∠2=∠__4__(两直线平行,内错角相等),
且DE∥AC,
∴∠4=∠__A__(两直线平行,同位角相等).
∴∠2=∠A(等量代换).
∵∠1+∠2+∠3=180°,
∴∠A+∠B+∠C=180°(等量代换).
22.(8分)如图,已知AC∥DE,AD∥BE,试说明∠BAC=∠B+∠E的理由.
解:∵AC∥DE,
∴∠1=∠D.
∵AD∥BE,
∴∠2=∠B,∠D=∠E.
∴∠1=∠E.
∵∠BAC=∠1+∠2,
∴∠BAC=∠B+∠E.
23.(8分)如图,在A、B两地之间要修建一条笔直的公路,从A地测得公路走向是北偏东48°,A、B两地同时开工,若干天后公路准确接通.
(1)B地所修公路的走向是南偏西多少?为什么?
(2)若公路AB长8千米,另一公路BC长6千米,且BC的走向是北偏西42°,试求A地到公路BC的距离.
解:(1)B地所修公路的走向是南偏西48°,
理由是:两直线平行,内错角相等;
∠ABC=180°-42°-48°=90°,
故A到BC的距离为AB的长度,即8千米.
24.(8分)如图,已知∠1=∠2,∠C=∠D,证明:∠A=∠F.
证明:因为∠1=∠2,∠2=∠3,
所以∠1=∠3,所以BD∥CE.
所以∠4=∠C.
又因为∠C=∠D,
所以∠4=∠D,
所以DF∥AC,
所以∠A=∠F.
25.(10分)如图,直线EF,CD相交于点O,OA⊥OB,且OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?
解:(1)因为∠AOE+∠AOF=180°,∠AOE=40°,
所以∠AOF=140°.
又因为OC平分∠AOF,
所以∠AOC=∠AOF=70°.
因为OA⊥OB,所以∠AOB=90°.
所以∠BOD=180°-∠AOC-∠AOB=180°-70°-90°=20°.
(2)因为∠AOE+∠AOF=180°,∠AOE=α,
所以∠AOF=180°-α.
又因为OC平分∠AOF,
所以∠AOC=∠AOF=90°-α.
因为OA⊥OB,所以∠AOB=90°.
所以∠BOD=180°-∠AOC-∠AOB=180°-(90°-α)-90°=α.
(3)从(1)(2)的结果中能看出∠AOE=2∠BOD.
26.(10分)已知直线l1∥l2,直线GH分别交l1、l2于A、B两点,直线MN分别交l1、l2于C、D两点,点P在直线MN上(点P和C、D不重合).
(1)如图,当点P在线段CD上时,试找出∠PAC、∠PBD、∠APB之间的关系并说出理由;
(2)当点P不在线段CD上时,试探究∠PAC、∠PBD、∠APB之间的关系(只写出结论,不说明理由).
解:(1)∠PAC+∠PBD=∠APB.
理由如下:作PQ∥l1,交AB与点Q,则PQ∥l1∥l2.
∴∠PAC=∠APQ,∠PBD=∠BPQ.
∵∠APQ+∠BPQ=∠APB,
∴∠PAC+∠PBD=∠APB.
(2)当点P在线段DC的延长线上时,∠PAC+∠APB=∠PBD;
当点P在线段CD的延长线上时,∠PAC=∠APB+∠PBD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
