苏科版九年级上册11.2滑轮同步练习(有解析)
文档属性
| 名称 | 苏科版九年级上册11.2滑轮同步练习(有解析) |  | |
| 格式 | docx | ||
| 文件大小 | 716.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-16 06:16:10 | ||
图片预览

文档简介
苏科版九年级上册 11.2 滑轮 同步练习
一、单选题
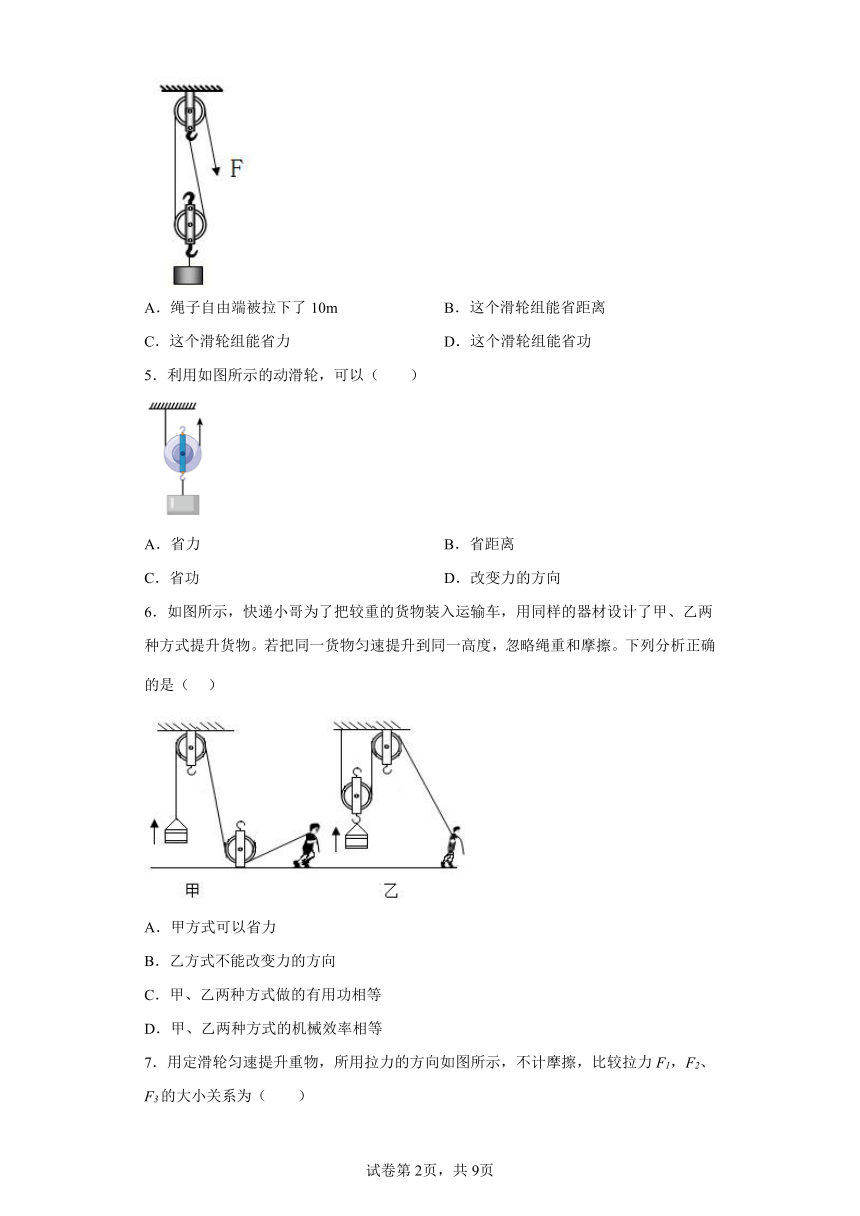
1.如图所示,用此滑轮组匀速拉动重物,关于此滑轮组,下列说法正确的是( )
A.使用该滑轮组不能省力 B.使用该滑轮组可以改变用力方向
C.使用该滑轮组可以省距离 D.使用该滑轮组可以省功
2.如图示,同一物体沿相同水平地面被滑轮或滑轮组匀速拉动,拉力分别为F1、F2、F3,不计滑轮与轴及轻绳间的摩擦,比较它们的大小,则( )
A.F1<F2<F3 B.F1>F2=F3 C.F2>F1>F3 D.F1=F2>F3
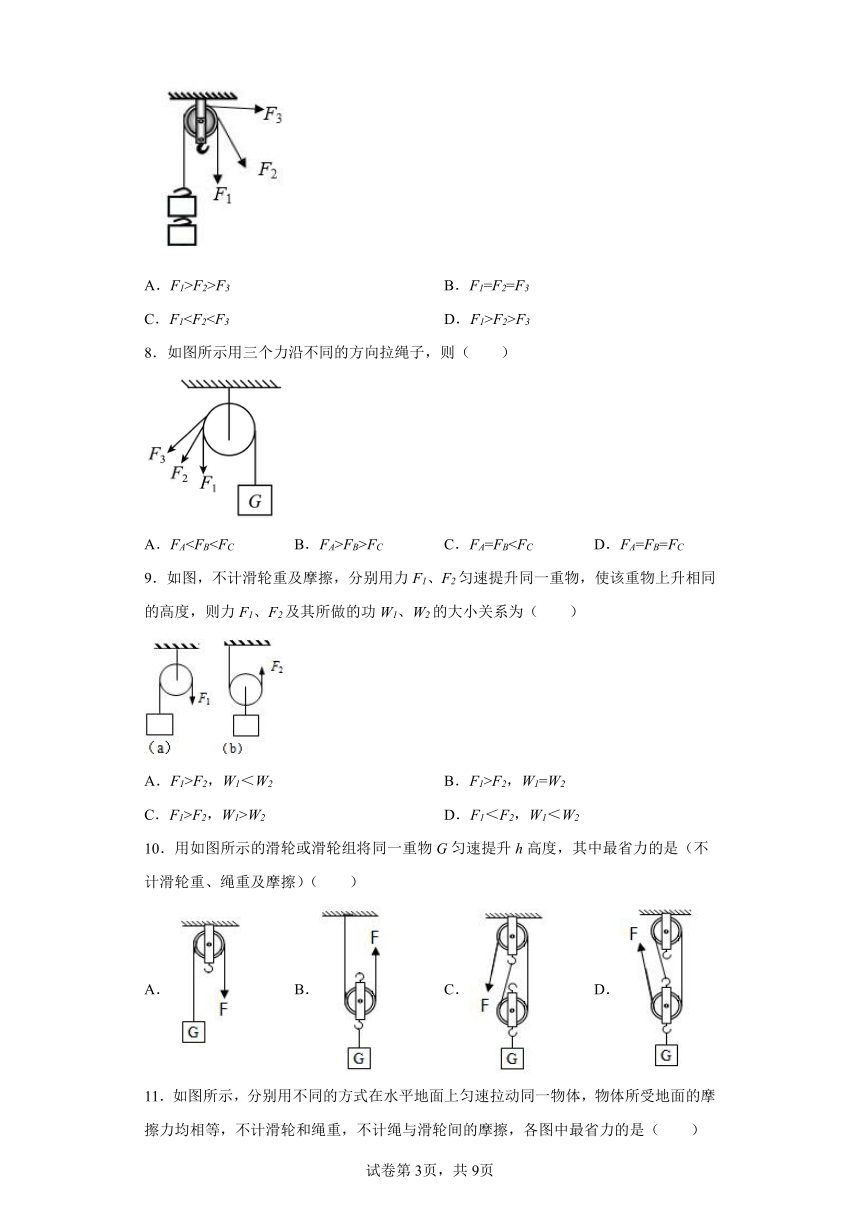
3.在探究使用滑轮组时拉力与物重的关系活动中,瑞瑞同学在与动滑轮相切的细绳上作一标记A,如图甲所示。然后用大小为F的拉力匀速竖直向上提升总重为G的钩码,当钩码上升的高度为H时,瑞瑞同学在与动滑轮相切的细绳上作另一标记B,并测得AB两点间的距离为2H,如图乙所示。(不计摩擦与绳重),则以下物理量正确的是( )
A.拉力F=G B.拉力F=G
C.绳自由端移动距离为2H D.绳自由端移动距离为3H
4.在有着“世界工厂”之称的东莞,车间工人们用如图所示的滑轮组把重物提起2m的高度,下列关于这个滑轮组工作的说法中,正确的是( )
A.绳子自由端被拉下了10m B.这个滑轮组能省距离
C.这个滑轮组能省力 D.这个滑轮组能省功
5.利用如图所示的动滑轮,可以( )
A.省力 B.省距离
C.省功 D.改变力的方向
6.如图所示,快递小哥为了把较重的货物装入运输车,用同样的器材设计了甲、乙两种方式提升货物。若把同一货物匀速提升到同一高度,忽略绳重和摩擦。下列分析正确的是( )
A.甲方式可以省力
B.乙方式不能改变力的方向
C.甲、乙两种方式做的有用功相等
D.甲、乙两种方式的机械效率相等
7.用定滑轮匀速提升重物,所用拉力的方向如图所示,不计摩擦,比较拉力F1,F2、F3的大小关系为( )
A.F1>F2>F3 B.F1=F2=F3
C.F1F2>F3
8.如图所示用三个力沿不同的方向拉绳子,则( )
A.FAFB>FC C.FA=FB9.如图,不计滑轮重及摩擦,分别用力F1、F2匀速提升同一重物,使该重物上升相同的高度,则力F1、F2及其所做的功W1、W2的大小关系为( )
A.F1>F2,W1<W2 B.F1>F2,W1=W2
C.F1>F2,W1>W2 D.F1<F2,W1<W2
10.用如图所示的滑轮或滑轮组将同一重物G匀速提升h高度,其中最省力的是(不计滑轮重、绳重及摩擦)( )
A. B. C. D.
11.如图所示,分别用不同的方式在水平地面上匀速拉动同一物体,物体所受地面的摩擦力均相等,不计滑轮和绳重,不计绳与滑轮间的摩擦,各图中最省力的是( )
A. B.
C. D.
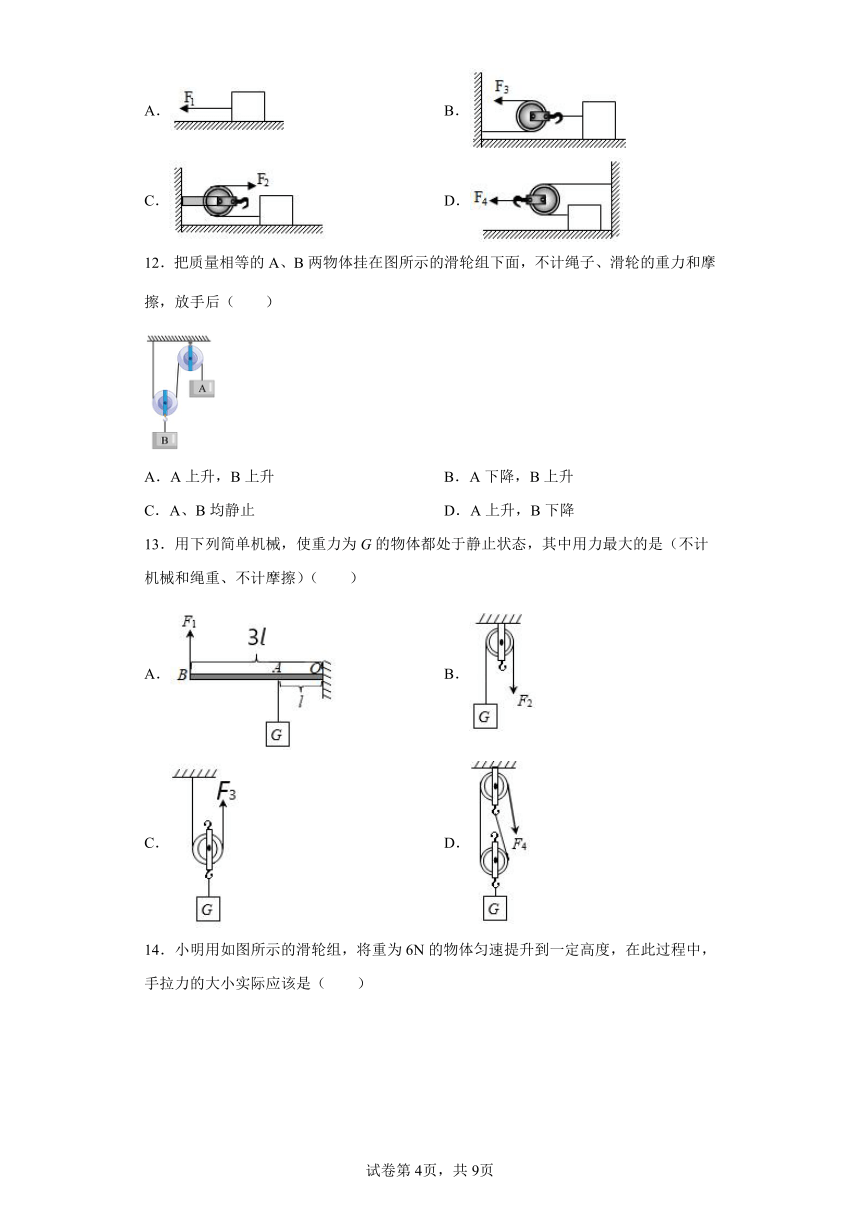
12.把质量相等的A、B两物体挂在图所示的滑轮组下面,不计绳子、滑轮的重力和摩擦,放手后( )
A.A上升,B上升 B.A下降,B上升
C.A、B均静止 D.A上升,B下降
13.用下列简单机械,使重力为G的物体都处于静止状态,其中用力最大的是(不计机械和绳重、不计摩擦)( )
A. B.
C. D.
14.小明用如图所示的滑轮组,将重为6N的物体匀速提升到一定高度,在此过程中,手拉力的大小实际应该是( )
A.小于3N B.等于2N C.大于2N D.大于3N
15.如图是学校旗杆顶上的一个滑轮,升旗时往下拉动绳子,国旗就会上升。下列对于滑轮的说法,正确的是( )
A.这是一个定滑轮,可省力 B.这是一个动滑轮,可省力
C.这是一个定滑轮,可改变力的方向 D.这是一个动滑轮,可改变力的方向
二、填空题
16.如图所示,滑轮_____可以看作等臂杠杆(选填“A”或“B”);若物体所受重力均为20 牛且处于静止状态,不计摩擦和滑轮重力,力F1的大小为_____牛,力F2的大小为_____牛。若物体上升高度为2米,则绳子自由端上升高度sA=_____米,sB=_____米。
17.如图所示,水平向右的拉力F作用于物块A,通过动滑轮拉动着B向右做匀速直线运动,使B物体在3s内向右移动了4.5m,地面对B的摩擦力大小是4N,拉力F大小等于20N;在滑轮重、绳重和绳与滑轮摩擦不计的情况下,则A受到的摩擦力大小_____N,拉力F的功率是______W。
18.如图甲所示,拉力F拉着轻质滑轮匀速上升,物体A的重力为28N,滑轮的半径为0.1m,在物理学中,我们将力和力臂的乘积称为力矩,单位是N·m,如果将滑轮看成是一个轻质杠杆,如图乙所示,则拉力F的力矩为______N·m。
19.动滑轮的实质是不等臂杠杆,如图所示使用方法,它的动力臂是动滑轮的______(选填“直径”或“半径”) ,阻力臂是动滑轮的______(选填“直径”或“半径”)
20.如图所示,利用滑轮起吊重物。该滑轮为______(选填“动”或“定”)滑轮;若弹簧测力计的拉力为图所示大小时,重物能在空中静止,则重物及滑轮的总重为______N。
三、综合题
21.力对物体转动的影响,不仅跟力的大小有关,还跟力和转动轴之间的距离(由力的方向和作用点决定)有关.力越大,力到转动轴的距离越大,力使物体转动的作用效果越明显.从转动轴到力的作用线的距离,叫力臂;力和力臂的乘积叫力矩,用M表示,M=F×L.力矩的单位是N m.
(1)如图甲是力F作用在水平杠杠上的示意图.OB的长度为L,力F与OB的夹角为30°,请在图中画出F的力臂,并推导出力F的力矩表达式.
(2)如图乙是摩擦传动的示意图,主动轮半径为0.04m,从动轮半径为0.12m,它们接触位置相互摩擦力的大小是50N,则这一对摩擦力对主动轮和从动轮的转轴的力矩分别为多少?
22.用如图所示的滑轮组来提升重物.
(1)作图与填空:
①请在图上画出最省力的绕绳方式;
( )
②在这种情况下,承担物体和动滑轮总重的绳子是________段.
(2)按照最省力的绕法,若用300 N的拉力,在5 s内将重为810 N的物体提高1 m,求:
①拉力做的功____;
②拉力的功率_____;
③滑轮组的机械效率_______.
(3)小明同学认为:根据题目条件,还可以求出动滑轮重.他求解的过程如下:由F拉=(G动+G物)得:G动=3F拉-G物=3×300 N-810 N=90 N.你认为小明这样求解正确吗____ 请说明理由_____.
23.O为支点的轻质杠杆原处于水平静止
(1)在杠杆左边某处挂上的钩码,在另一处施加力F,图甲、乙、丙三个情景中可以使杠杆仍处于水平静止的是图______(选填编号)
(2)如图丁,分别在杠杆上的A、B两点施加力、,使杠杆水平静止,测得与的大小相等(F2未画出).
①画出的力臂
( )
②F2的力臂l2______l1 (选填“”、“”、“” )
24.如图,分别使用轻质定滑轮、轻质动滑轮竖直提升G=10N的重物,使其匀速上升2m.不计滑轮与轴的摩擦和滑轮自重,F1=10N、F2=5N。
(1)请运用杠杆平衡原理作图分析:为什么动滑轮能省一半的力______;(在答卷上作答)
(2)若想进一步研究使用定滑轮时拉力大小是否与拉力方向有关,接下来的操作是______。
25.如图甲为塔式起重机简易示意图,塔式起重机主要用于房屋建筑中材料的输送及建筑构件的安装.(动滑轮重、绳重及摩擦不计,g取10N/kg)
(1)为保持平衡,起重臂的长度越短的塔式起重机,配备的平衡重的质量应越______(选填“大”或“小”).
(2)图乙为起重机钢丝绳穿绳简化示意图,滑轮a的作用是_____.若钢丝绳能承受的最大拉力为2.5×104N,则能吊起货物的质量不能超过_____千克.
(3)若将重为2×104N的货物由地面沿竖直方向匀速提升20m,再沿水平方向移动10m,则此过程钢丝绳做功多少焦________
(4)若该塔式电动机的效率为90%,将重为1.2×104N的货物提升到30m的高度,用时50s,则该起升电动机的实际功率是多少瓦_________
26.“低头族”长时间低头看手机,会引起颈部肌肉损伤.当头颅为竖直状态时,颈部肌肉的拉力为零,当头颅低下时,颈部肌肉会产生一定的拉力.为了研究颈部肌肉的拉力与低头角度大小的关系,我们可以建立一个头颅模型来模拟实验.如图甲所示,把人的颈椎简化成一个支点O,用1kg的头颅模型在重力作用下绕着这个支点O转动,A点为头颅模型的重心,B点为肌肉拉力的作用点.将细线的一端固定在B点,用弹簧测力计拉着细线模拟测量肌肉的拉力,头颅模型在转动过程中,细线拉力的方向始终垂直于OB,如图乙所示,让头颅模型从竖直状态开始转动,通过实验记录出低头角度θ及细线拉力F的数据,如下表:
低头角度θ/° 0 15 30 45 60
细线拉力F/N 0 7.3 14.0 20.2 25.0
(1)设头颅质量为8kg,OA长14cm,OB长4cm.当低头角度为30°时,颈部肌肉实际承受的拉力是_____N.
(2)在图乙中画出细线拉力的示意图.
( )
(3)低头角度越大,颈部肌肉的拉力_____.
(4)请你就预防和延缓颈椎损伤提出一个合理化的建议:_____.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【详解】
A.该滑轮组动滑轮上有三条绳分担力,自由端的拉力为直接拉动物体和动滑轮总重的三分之一,所以省力,故A错误;
B.滑轮组可以改变力的方向,如图,拉动物体向上,此时通过滑轮组拉力的方向仍然向上,没有改变力的方向,若绕线从定滑轮开始,自由端拉力的方向向下,改变了力的方向,故B正确;
CD.该滑轮组可以省力,若又省距离,也就是省功,根据能量守恒定律,这样的机械是不存在的,故CD错误;
故选B。
2.C
【详解】
不计滑轮与轴及轻绳间的摩擦,假设物块与地面的摩擦力为f,由于第一个图中滑轮为定滑轮,使用过程不省力,故
F1=f
第二个图中滑轮为动滑轮,但F2处作用在动滑轮上,费2倍的力,所以
F2=2f
第三个图中滑轮为动滑轮,省一半的力,则
故F2>F1>F3,故C正确。
故选C。
3.D
【详解】
AB.由图知,物体和动滑轮的总重由三段绳子承担,不计摩擦与绳重,拉力
F=(G+G动)
故AB错误;
CD.图中AB两点间的距离为2H,这并不是绳子自由端移动的距离,绳子自由端移动的距离应该为原来的A点到现在A点的竖直距离;钩码升高H,则绳子自由端移动的距离为
s=3H
故C错误,D正确。
故选D。
4.C
【详解】
A.由图知,n=2,物体上升的高度h=2m,则绳子自由端移动的距离
s=2h=2×2m=4 m
即绳子自由端被拉下了4m,故A错误;
BC.图中滑轮组可以省力但费距离,故B错误、C正确;
D.使用任何机械都不省功,D错误。
故选C。
5.A
【详解】
如图所示是动滑轮,由动滑轮的工作特点可知,使用动滑轮不能改变力的方向且费距离,但可以省力,属于简单机械不能省功;所以人们使用动滑轮是利用它能省力的特点。故A符合题意,BCD不符合题意。
故选A。
6.C
【详解】
A.由图可知,甲方式是两个定滑轮,定滑轮的本质是等臂杠杆,不能省力,故A错误;
B.乙方式是一个动滑轮和定滑轮组成的滑轮组,不仅可以省力,也可以改变力的方向,故B错误;
C.由题可知,甲乙两滑轮组均将相同物体提升相同高度,由可知;故C正确;
D.由图可知,甲方式是两个定滑轮,乙方式是一个动滑轮和定滑轮组成的滑轮组,乙方式做的额外功大于甲方式,有用功相同、总功不相同,根据可知,两个滑轮组的机械效率不相等,故D错误。
故选C。
7.B
【详解】
由于定滑轮相当于一等臂杠杆,只能改变力的方向,而不省力,使用定滑轮沿三个不同方向拉同一重物G,动力臂长度不变,所以用的拉力大小相等,即F1、F2、F3都等于物体的重力,故B正确。
故选B。
8.D
【详解】
定滑轮是一个等臂杠杆,不能省力,但能改变力的方向,所以三个方向的拉力都等于重物的重力。故D符合题意,ABC不符合题意。
故选D。
9.B
【详解】
因为使用定滑轮不省力,所以F1=G;因为使用动滑轮能省一半力,所以不计滑轮重及摩擦,因此F1>F2。不计滑轮重及摩擦,同一重物,用动滑轮和动滑轮提升的高度相同,它们克服物体的重力做的功相同,所以
W1=W2=Gh
故选B。
10.D
【详解】
由题知,不计摩擦和动滑轮重。
A.使用的是定滑轮,F=G;
B.使用的是动滑轮,F=G;
C.使用的是滑轮组,n=2,F=G;
D.使用的是滑轮组,n=3,F=G;
由此可知D图中最省力,F=G。
故选D。
11.B
【详解】
由题知,物体所受地面的摩擦力均相等,设摩擦力大小均为f;
A.用力匀速拉动物体时,物体受到的拉力和摩擦力为一对平衡力,大小相等,拉力F1=f;
B.图中使用的是动滑轮,不计滑轮和绳重,不计绳与滑轮间的摩擦,拉力;
C.图中使用的是定滑轮,不计滑轮和绳重,不计绳与滑轮间的摩擦,拉力F2=f;
D.图中使用的是动滑轮,但动力作用在轴上,不计滑轮和绳重,不计绳与滑轮间的摩擦,则拉力F4=2f,故B最省力。
故选B。
12.B
【详解】
设两个物体的重力均为G,则绳子受到的拉力为
动滑轮受到两根绳子向上的拉力F,B对动滑轮的向下的拉力大小为G,所以
故动滑轮会向上运动,即B上升,则A下降。故ACD不符合题意,B符合题意。
故选B。
13.B
【详解】
由题知,不计机械和绳重、不计摩擦时:A图中动力臂等于3倍阻力臂,由杠杆平衡条件可知,F1G;B图中使用定滑轮不能省力,F2=G;C图中使用动滑轮省一半力,F3G;D图中使用滑轮组,n=2,F4G;由以上分析可知用力最大的是图B。
故选B。
14.D
【详解】
由图可知,滑轮组承担物重的绳子段数n=2,因为动滑轮重、绳重和摩擦都考虑在内,所以实际拉力
故D符合题意。
故选D。
15.C
【详解】
旗杆顶上滑轮的轴固定在旗杆上,所以该滑轮是一个定滑轮,定滑轮不能省力,其优点是可以改变力的方向。
故选C。
16. A 20 10 2 4
【详解】
[1] 由图可知,A的轴固定 ,为定滑轮,本质是等臂杠杆;B与物体一起上升,是动滑轮,本质是动力臂是阻力臂二倍的省力杠杆。
[2] 不计摩擦,使用定滑轮不省力也不费力,故
F1=G=20N
力F1的大小为20N。
[3]不计摩擦和滑轮重力,B是动滑轮可以省一半的力,因此
F2=×20N=10N
力F2的大小为10N。
[4]A是定滑轮,若物体上升高度为2米,则绳子自由端上升高度
sA=h=2m
sA为2米。
[5]B是动滑轮, 若物体上升高度为2米,则绳子自由端上升高度
sB=2h=22m=4m
sB为4米。
17. 12 15
【详解】
[1]图中滑轮是动滑轮,在滑轮重、绳重和绳与滑轮摩擦不计的情况下,动滑轮轴上的拉力
F拉=2f=2×4N=8N
由力的作用相互性可知,物体A受到绳子的拉力
F′拉=F拉=8N
物块A做匀速直线运动,水平方向上受到拉力F、绳的拉力和地面的摩擦力是平衡力,A受到的摩擦力大小
fA=F-F′拉=20N-8N=12N
[2]B物体移动的速度
A的速度
=0.75m/s
拉力F的功率
=FvA=20N×0.75m/s=15W
18.5.6
【详解】
由图知,力F作用在动滑轮的轴上,根据动滑轮的特点可得,,则拉力F为
F=nG=2×28N=56N
由图可知,拉力F的力臂为0.1m,由力和力臂的乘积称为力矩可知,拉力F的力矩为
56N×0.1m=5.6N·m
19. 直径 半径
【详解】
[1][2]动滑轮的支点o在绳与动滑轮最左边的接触点,动力的作用点在绳与动滑轮最右边的接触点,支点到动力作用线的距离为动力臂,即动滑轮的直径。物体对滑轮的拉力为阻力,作用点在动滑轮的轴心,支点到阻力作用线的距离为阻力臂,即动滑轮的半径。
20. 动 4.8
【详解】
[1]工作时,滑轮的轴随物体一起运动,为动滑轮。
[2]拉力大小为2.4N,重物及滑轮的总重为
G+G动=2F=2×2.4N=4.8N
21.(1)
M=1/2 FL
(2)主动轮:M=FL=50N×0.04m=2N M 从动轮:M=FL=50N×0.12m=6N M
【详解】
(1)延长拉力作用线F,过支点O做拉力作用线F的垂线,即为拉力F的力臂,如图:
;
由于力F与OB的夹角为30°,根据数学知识可知,F的力臂的长度为L,
F的力矩表达式为:
M=FL;
(2)力和力臂的乘积叫力矩,则主动轮的力矩:
M=FL=50N×0.04m=2N M;
从动轮的力矩为:
M=FL=50N×0.12m=6N M.
22. 见解析 3 900 J 180 W 90% 不正确;题中未说明摩擦不计.
【详解】
①要使承担物重的绳子段数最多,应从动滑轮绕起,如图所示:
②由图知,滑轮组由3段绳子承担物重;
(2)①s=3h=3×1 m=3 m,W总=Fs=300 N×3 m=900 J;
②P总==180 W;
③W有用=Gh=810 N×1 m=810 J,
η=×100%=×100%=90%;
(3)由于绳子具有重力,轮和轴、轮和绳子之间存在摩擦力,所以用公式F拉=(G动+G物)求出动滑轮的重力,是不正确的.
23. 甲、丙 =
根据杠杆的平衡条件可知,当杠杆两边钩码同时向远离支点方向移动相同的距离,力和力臂的乘积大的一端下沉;力臂的画法:首先根据杠杆的示意图,确定杠杆的支点;确定力的作用点和力的方向,画出力的作用线;从支点向力的作用线作垂线,支点到垂足的距离就是力臂.已知与的大小关系,根据杠杆平衡条件分析和的大小关系.
【详解】
杠杆一个格的长度为L,图甲中,左端力与力臂的乘积为,右端力与力臂的乘积为,则杠杆平衡;图乙中,由于左、右边的力都是使杠杆沿逆时针方向转动,所以杠杆不平衡,会沿逆时针方向转动;图丙中左端力与力臂的乘积为,右端力与力臂的乘积为,则杠杆平衡,故杠杆仍处于水平静止的是图甲和丙;
支点为O,从O做的垂线段就是的力臂L1,如下图所示:
杠杆水平静止,测得与的大小相等,根据可得:.
24. 改变F1方向,仍匀速拉动物体上升,比较F1大小是否改变
【详解】
试题分析:(1)滑轮实质上是个杠杆, 支点为O, 动力臂为L1, 阻力臂为L2, 物体匀速上升时,滑轮匀速转动,处于杠杆平衡,F1L1=F2L2, L1=2L2 ,则 F1="1/2" F2,故动滑轮可省一半的力;
(2)要想比较 拉力大小是否与拉力方向有关,所以应改变F1方向,仍匀速拉动物体上升,比较F1大小是否改变.
考点:滑轮与杠杆
25. 小 省力 5×103kg 4×105J 8×103W
【详解】
(1)由杠杆的平衡条件F1L1=F2L2可得: ,由此可知当阻力臂和动力不变时,阻力与动力臂成正比,即动力臂越大,阻力越大;动力臂越小,阻力越小,故为保持平衡,起重臂的长度越短的塔式起重机,配备的平衡重的质量应越小;
(2)图示中滑轮a为动滑轮,其作用是省力,可以省一半的力;由题意可知该滑轮组承担总重的绳子有2段,故G=2F=2.5×104N×2=5×104N,由G=mg可得:=5×103kg;
(3) 钢丝绳做功:W=Fs=Gh=2×104N ×20m=4×105J,由于水平移动时,重力方向上没移动距离,故水平移动过程中钢丝绳没做功;
(4) 电动机的有用功:W有用=Gh=1.2×104N×30m=3.6×105J,电动机的总功: =4×105J,电动机的实际功率: =8000W.
26. 112 越大 尽量减小低头的角度(或不要长时间低头做事,低头时间久了要抬头休息等等)
【详解】
(1)由表格中数据知,当低头角度为30°时,若m=1kg,细线的拉力为14N;
若m=8kg,由于角度不变,所以动力臂和阻力臂不变,则拉力F=8×14N=112N;
(2)由题意知,细线拉力的方向应垂直于OB向下,如图所示:
(3)图乙中,F的力臂为OB,做出乙图中G的力臂LG,如图所示:
根据杠杆的平衡条件可得:G LG=F LF,则,人低头的角度越大,sinθ越大,则G的力臂越大,肌肉的拉力就越大;
(4)要预防和延缓颈椎损伤,可尽量减小低头的角度,不要长时间低头做事,低头时间久了要抬头休息等等.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图所示,用此滑轮组匀速拉动重物,关于此滑轮组,下列说法正确的是( )
A.使用该滑轮组不能省力 B.使用该滑轮组可以改变用力方向
C.使用该滑轮组可以省距离 D.使用该滑轮组可以省功
2.如图示,同一物体沿相同水平地面被滑轮或滑轮组匀速拉动,拉力分别为F1、F2、F3,不计滑轮与轴及轻绳间的摩擦,比较它们的大小,则( )
A.F1<F2<F3 B.F1>F2=F3 C.F2>F1>F3 D.F1=F2>F3
3.在探究使用滑轮组时拉力与物重的关系活动中,瑞瑞同学在与动滑轮相切的细绳上作一标记A,如图甲所示。然后用大小为F的拉力匀速竖直向上提升总重为G的钩码,当钩码上升的高度为H时,瑞瑞同学在与动滑轮相切的细绳上作另一标记B,并测得AB两点间的距离为2H,如图乙所示。(不计摩擦与绳重),则以下物理量正确的是( )
A.拉力F=G B.拉力F=G
C.绳自由端移动距离为2H D.绳自由端移动距离为3H
4.在有着“世界工厂”之称的东莞,车间工人们用如图所示的滑轮组把重物提起2m的高度,下列关于这个滑轮组工作的说法中,正确的是( )
A.绳子自由端被拉下了10m B.这个滑轮组能省距离
C.这个滑轮组能省力 D.这个滑轮组能省功
5.利用如图所示的动滑轮,可以( )
A.省力 B.省距离
C.省功 D.改变力的方向
6.如图所示,快递小哥为了把较重的货物装入运输车,用同样的器材设计了甲、乙两种方式提升货物。若把同一货物匀速提升到同一高度,忽略绳重和摩擦。下列分析正确的是( )
A.甲方式可以省力
B.乙方式不能改变力的方向
C.甲、乙两种方式做的有用功相等
D.甲、乙两种方式的机械效率相等
7.用定滑轮匀速提升重物,所用拉力的方向如图所示,不计摩擦,比较拉力F1,F2、F3的大小关系为( )
A.F1>F2>F3 B.F1=F2=F3
C.F1
8.如图所示用三个力沿不同的方向拉绳子,则( )
A.FA
A.F1>F2,W1<W2 B.F1>F2,W1=W2
C.F1>F2,W1>W2 D.F1<F2,W1<W2
10.用如图所示的滑轮或滑轮组将同一重物G匀速提升h高度,其中最省力的是(不计滑轮重、绳重及摩擦)( )
A. B. C. D.
11.如图所示,分别用不同的方式在水平地面上匀速拉动同一物体,物体所受地面的摩擦力均相等,不计滑轮和绳重,不计绳与滑轮间的摩擦,各图中最省力的是( )
A. B.
C. D.
12.把质量相等的A、B两物体挂在图所示的滑轮组下面,不计绳子、滑轮的重力和摩擦,放手后( )
A.A上升,B上升 B.A下降,B上升
C.A、B均静止 D.A上升,B下降
13.用下列简单机械,使重力为G的物体都处于静止状态,其中用力最大的是(不计机械和绳重、不计摩擦)( )
A. B.
C. D.
14.小明用如图所示的滑轮组,将重为6N的物体匀速提升到一定高度,在此过程中,手拉力的大小实际应该是( )
A.小于3N B.等于2N C.大于2N D.大于3N
15.如图是学校旗杆顶上的一个滑轮,升旗时往下拉动绳子,国旗就会上升。下列对于滑轮的说法,正确的是( )
A.这是一个定滑轮,可省力 B.这是一个动滑轮,可省力
C.这是一个定滑轮,可改变力的方向 D.这是一个动滑轮,可改变力的方向
二、填空题
16.如图所示,滑轮_____可以看作等臂杠杆(选填“A”或“B”);若物体所受重力均为20 牛且处于静止状态,不计摩擦和滑轮重力,力F1的大小为_____牛,力F2的大小为_____牛。若物体上升高度为2米,则绳子自由端上升高度sA=_____米,sB=_____米。
17.如图所示,水平向右的拉力F作用于物块A,通过动滑轮拉动着B向右做匀速直线运动,使B物体在3s内向右移动了4.5m,地面对B的摩擦力大小是4N,拉力F大小等于20N;在滑轮重、绳重和绳与滑轮摩擦不计的情况下,则A受到的摩擦力大小_____N,拉力F的功率是______W。
18.如图甲所示,拉力F拉着轻质滑轮匀速上升,物体A的重力为28N,滑轮的半径为0.1m,在物理学中,我们将力和力臂的乘积称为力矩,单位是N·m,如果将滑轮看成是一个轻质杠杆,如图乙所示,则拉力F的力矩为______N·m。
19.动滑轮的实质是不等臂杠杆,如图所示使用方法,它的动力臂是动滑轮的______(选填“直径”或“半径”) ,阻力臂是动滑轮的______(选填“直径”或“半径”)
20.如图所示,利用滑轮起吊重物。该滑轮为______(选填“动”或“定”)滑轮;若弹簧测力计的拉力为图所示大小时,重物能在空中静止,则重物及滑轮的总重为______N。
三、综合题
21.力对物体转动的影响,不仅跟力的大小有关,还跟力和转动轴之间的距离(由力的方向和作用点决定)有关.力越大,力到转动轴的距离越大,力使物体转动的作用效果越明显.从转动轴到力的作用线的距离,叫力臂;力和力臂的乘积叫力矩,用M表示,M=F×L.力矩的单位是N m.
(1)如图甲是力F作用在水平杠杠上的示意图.OB的长度为L,力F与OB的夹角为30°,请在图中画出F的力臂,并推导出力F的力矩表达式.
(2)如图乙是摩擦传动的示意图,主动轮半径为0.04m,从动轮半径为0.12m,它们接触位置相互摩擦力的大小是50N,则这一对摩擦力对主动轮和从动轮的转轴的力矩分别为多少?
22.用如图所示的滑轮组来提升重物.
(1)作图与填空:
①请在图上画出最省力的绕绳方式;
( )
②在这种情况下,承担物体和动滑轮总重的绳子是________段.
(2)按照最省力的绕法,若用300 N的拉力,在5 s内将重为810 N的物体提高1 m,求:
①拉力做的功____;
②拉力的功率_____;
③滑轮组的机械效率_______.
(3)小明同学认为:根据题目条件,还可以求出动滑轮重.他求解的过程如下:由F拉=(G动+G物)得:G动=3F拉-G物=3×300 N-810 N=90 N.你认为小明这样求解正确吗____ 请说明理由_____.
23.O为支点的轻质杠杆原处于水平静止
(1)在杠杆左边某处挂上的钩码,在另一处施加力F,图甲、乙、丙三个情景中可以使杠杆仍处于水平静止的是图______(选填编号)
(2)如图丁,分别在杠杆上的A、B两点施加力、,使杠杆水平静止,测得与的大小相等(F2未画出).
①画出的力臂
( )
②F2的力臂l2______l1 (选填“”、“”、“” )
24.如图,分别使用轻质定滑轮、轻质动滑轮竖直提升G=10N的重物,使其匀速上升2m.不计滑轮与轴的摩擦和滑轮自重,F1=10N、F2=5N。
(1)请运用杠杆平衡原理作图分析:为什么动滑轮能省一半的力______;(在答卷上作答)
(2)若想进一步研究使用定滑轮时拉力大小是否与拉力方向有关,接下来的操作是______。
25.如图甲为塔式起重机简易示意图,塔式起重机主要用于房屋建筑中材料的输送及建筑构件的安装.(动滑轮重、绳重及摩擦不计,g取10N/kg)
(1)为保持平衡,起重臂的长度越短的塔式起重机,配备的平衡重的质量应越______(选填“大”或“小”).
(2)图乙为起重机钢丝绳穿绳简化示意图,滑轮a的作用是_____.若钢丝绳能承受的最大拉力为2.5×104N,则能吊起货物的质量不能超过_____千克.
(3)若将重为2×104N的货物由地面沿竖直方向匀速提升20m,再沿水平方向移动10m,则此过程钢丝绳做功多少焦________
(4)若该塔式电动机的效率为90%,将重为1.2×104N的货物提升到30m的高度,用时50s,则该起升电动机的实际功率是多少瓦_________
26.“低头族”长时间低头看手机,会引起颈部肌肉损伤.当头颅为竖直状态时,颈部肌肉的拉力为零,当头颅低下时,颈部肌肉会产生一定的拉力.为了研究颈部肌肉的拉力与低头角度大小的关系,我们可以建立一个头颅模型来模拟实验.如图甲所示,把人的颈椎简化成一个支点O,用1kg的头颅模型在重力作用下绕着这个支点O转动,A点为头颅模型的重心,B点为肌肉拉力的作用点.将细线的一端固定在B点,用弹簧测力计拉着细线模拟测量肌肉的拉力,头颅模型在转动过程中,细线拉力的方向始终垂直于OB,如图乙所示,让头颅模型从竖直状态开始转动,通过实验记录出低头角度θ及细线拉力F的数据,如下表:
低头角度θ/° 0 15 30 45 60
细线拉力F/N 0 7.3 14.0 20.2 25.0
(1)设头颅质量为8kg,OA长14cm,OB长4cm.当低头角度为30°时,颈部肌肉实际承受的拉力是_____N.
(2)在图乙中画出细线拉力的示意图.
( )
(3)低头角度越大,颈部肌肉的拉力_____.
(4)请你就预防和延缓颈椎损伤提出一个合理化的建议:_____.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【详解】
A.该滑轮组动滑轮上有三条绳分担力,自由端的拉力为直接拉动物体和动滑轮总重的三分之一,所以省力,故A错误;
B.滑轮组可以改变力的方向,如图,拉动物体向上,此时通过滑轮组拉力的方向仍然向上,没有改变力的方向,若绕线从定滑轮开始,自由端拉力的方向向下,改变了力的方向,故B正确;
CD.该滑轮组可以省力,若又省距离,也就是省功,根据能量守恒定律,这样的机械是不存在的,故CD错误;
故选B。
2.C
【详解】
不计滑轮与轴及轻绳间的摩擦,假设物块与地面的摩擦力为f,由于第一个图中滑轮为定滑轮,使用过程不省力,故
F1=f
第二个图中滑轮为动滑轮,但F2处作用在动滑轮上,费2倍的力,所以
F2=2f
第三个图中滑轮为动滑轮,省一半的力,则
故F2>F1>F3,故C正确。
故选C。
3.D
【详解】
AB.由图知,物体和动滑轮的总重由三段绳子承担,不计摩擦与绳重,拉力
F=(G+G动)
故AB错误;
CD.图中AB两点间的距离为2H,这并不是绳子自由端移动的距离,绳子自由端移动的距离应该为原来的A点到现在A点的竖直距离;钩码升高H,则绳子自由端移动的距离为
s=3H
故C错误,D正确。
故选D。
4.C
【详解】
A.由图知,n=2,物体上升的高度h=2m,则绳子自由端移动的距离
s=2h=2×2m=4 m
即绳子自由端被拉下了4m,故A错误;
BC.图中滑轮组可以省力但费距离,故B错误、C正确;
D.使用任何机械都不省功,D错误。
故选C。
5.A
【详解】
如图所示是动滑轮,由动滑轮的工作特点可知,使用动滑轮不能改变力的方向且费距离,但可以省力,属于简单机械不能省功;所以人们使用动滑轮是利用它能省力的特点。故A符合题意,BCD不符合题意。
故选A。
6.C
【详解】
A.由图可知,甲方式是两个定滑轮,定滑轮的本质是等臂杠杆,不能省力,故A错误;
B.乙方式是一个动滑轮和定滑轮组成的滑轮组,不仅可以省力,也可以改变力的方向,故B错误;
C.由题可知,甲乙两滑轮组均将相同物体提升相同高度,由可知;故C正确;
D.由图可知,甲方式是两个定滑轮,乙方式是一个动滑轮和定滑轮组成的滑轮组,乙方式做的额外功大于甲方式,有用功相同、总功不相同,根据可知,两个滑轮组的机械效率不相等,故D错误。
故选C。
7.B
【详解】
由于定滑轮相当于一等臂杠杆,只能改变力的方向,而不省力,使用定滑轮沿三个不同方向拉同一重物G,动力臂长度不变,所以用的拉力大小相等,即F1、F2、F3都等于物体的重力,故B正确。
故选B。
8.D
【详解】
定滑轮是一个等臂杠杆,不能省力,但能改变力的方向,所以三个方向的拉力都等于重物的重力。故D符合题意,ABC不符合题意。
故选D。
9.B
【详解】
因为使用定滑轮不省力,所以F1=G;因为使用动滑轮能省一半力,所以不计滑轮重及摩擦,因此F1>F2。不计滑轮重及摩擦,同一重物,用动滑轮和动滑轮提升的高度相同,它们克服物体的重力做的功相同,所以
W1=W2=Gh
故选B。
10.D
【详解】
由题知,不计摩擦和动滑轮重。
A.使用的是定滑轮,F=G;
B.使用的是动滑轮,F=G;
C.使用的是滑轮组,n=2,F=G;
D.使用的是滑轮组,n=3,F=G;
由此可知D图中最省力,F=G。
故选D。
11.B
【详解】
由题知,物体所受地面的摩擦力均相等,设摩擦力大小均为f;
A.用力匀速拉动物体时,物体受到的拉力和摩擦力为一对平衡力,大小相等,拉力F1=f;
B.图中使用的是动滑轮,不计滑轮和绳重,不计绳与滑轮间的摩擦,拉力;
C.图中使用的是定滑轮,不计滑轮和绳重,不计绳与滑轮间的摩擦,拉力F2=f;
D.图中使用的是动滑轮,但动力作用在轴上,不计滑轮和绳重,不计绳与滑轮间的摩擦,则拉力F4=2f,故B最省力。
故选B。
12.B
【详解】
设两个物体的重力均为G,则绳子受到的拉力为
动滑轮受到两根绳子向上的拉力F,B对动滑轮的向下的拉力大小为G,所以
故动滑轮会向上运动,即B上升,则A下降。故ACD不符合题意,B符合题意。
故选B。
13.B
【详解】
由题知,不计机械和绳重、不计摩擦时:A图中动力臂等于3倍阻力臂,由杠杆平衡条件可知,F1G;B图中使用定滑轮不能省力,F2=G;C图中使用动滑轮省一半力,F3G;D图中使用滑轮组,n=2,F4G;由以上分析可知用力最大的是图B。
故选B。
14.D
【详解】
由图可知,滑轮组承担物重的绳子段数n=2,因为动滑轮重、绳重和摩擦都考虑在内,所以实际拉力
故D符合题意。
故选D。
15.C
【详解】
旗杆顶上滑轮的轴固定在旗杆上,所以该滑轮是一个定滑轮,定滑轮不能省力,其优点是可以改变力的方向。
故选C。
16. A 20 10 2 4
【详解】
[1] 由图可知,A的轴固定 ,为定滑轮,本质是等臂杠杆;B与物体一起上升,是动滑轮,本质是动力臂是阻力臂二倍的省力杠杆。
[2] 不计摩擦,使用定滑轮不省力也不费力,故
F1=G=20N
力F1的大小为20N。
[3]不计摩擦和滑轮重力,B是动滑轮可以省一半的力,因此
F2=×20N=10N
力F2的大小为10N。
[4]A是定滑轮,若物体上升高度为2米,则绳子自由端上升高度
sA=h=2m
sA为2米。
[5]B是动滑轮, 若物体上升高度为2米,则绳子自由端上升高度
sB=2h=22m=4m
sB为4米。
17. 12 15
【详解】
[1]图中滑轮是动滑轮,在滑轮重、绳重和绳与滑轮摩擦不计的情况下,动滑轮轴上的拉力
F拉=2f=2×4N=8N
由力的作用相互性可知,物体A受到绳子的拉力
F′拉=F拉=8N
物块A做匀速直线运动,水平方向上受到拉力F、绳的拉力和地面的摩擦力是平衡力,A受到的摩擦力大小
fA=F-F′拉=20N-8N=12N
[2]B物体移动的速度
A的速度
=0.75m/s
拉力F的功率
=FvA=20N×0.75m/s=15W
18.5.6
【详解】
由图知,力F作用在动滑轮的轴上,根据动滑轮的特点可得,,则拉力F为
F=nG=2×28N=56N
由图可知,拉力F的力臂为0.1m,由力和力臂的乘积称为力矩可知,拉力F的力矩为
56N×0.1m=5.6N·m
19. 直径 半径
【详解】
[1][2]动滑轮的支点o在绳与动滑轮最左边的接触点,动力的作用点在绳与动滑轮最右边的接触点,支点到动力作用线的距离为动力臂,即动滑轮的直径。物体对滑轮的拉力为阻力,作用点在动滑轮的轴心,支点到阻力作用线的距离为阻力臂,即动滑轮的半径。
20. 动 4.8
【详解】
[1]工作时,滑轮的轴随物体一起运动,为动滑轮。
[2]拉力大小为2.4N,重物及滑轮的总重为
G+G动=2F=2×2.4N=4.8N
21.(1)
M=1/2 FL
(2)主动轮:M=FL=50N×0.04m=2N M 从动轮:M=FL=50N×0.12m=6N M
【详解】
(1)延长拉力作用线F,过支点O做拉力作用线F的垂线,即为拉力F的力臂,如图:
;
由于力F与OB的夹角为30°,根据数学知识可知,F的力臂的长度为L,
F的力矩表达式为:
M=FL;
(2)力和力臂的乘积叫力矩,则主动轮的力矩:
M=FL=50N×0.04m=2N M;
从动轮的力矩为:
M=FL=50N×0.12m=6N M.
22. 见解析 3 900 J 180 W 90% 不正确;题中未说明摩擦不计.
【详解】
①要使承担物重的绳子段数最多,应从动滑轮绕起,如图所示:
②由图知,滑轮组由3段绳子承担物重;
(2)①s=3h=3×1 m=3 m,W总=Fs=300 N×3 m=900 J;
②P总==180 W;
③W有用=Gh=810 N×1 m=810 J,
η=×100%=×100%=90%;
(3)由于绳子具有重力,轮和轴、轮和绳子之间存在摩擦力,所以用公式F拉=(G动+G物)求出动滑轮的重力,是不正确的.
23. 甲、丙 =
根据杠杆的平衡条件可知,当杠杆两边钩码同时向远离支点方向移动相同的距离,力和力臂的乘积大的一端下沉;力臂的画法:首先根据杠杆的示意图,确定杠杆的支点;确定力的作用点和力的方向,画出力的作用线;从支点向力的作用线作垂线,支点到垂足的距离就是力臂.已知与的大小关系,根据杠杆平衡条件分析和的大小关系.
【详解】
杠杆一个格的长度为L,图甲中,左端力与力臂的乘积为,右端力与力臂的乘积为,则杠杆平衡;图乙中,由于左、右边的力都是使杠杆沿逆时针方向转动,所以杠杆不平衡,会沿逆时针方向转动;图丙中左端力与力臂的乘积为,右端力与力臂的乘积为,则杠杆平衡,故杠杆仍处于水平静止的是图甲和丙;
支点为O,从O做的垂线段就是的力臂L1,如下图所示:
杠杆水平静止,测得与的大小相等,根据可得:.
24. 改变F1方向,仍匀速拉动物体上升,比较F1大小是否改变
【详解】
试题分析:(1)滑轮实质上是个杠杆, 支点为O, 动力臂为L1, 阻力臂为L2, 物体匀速上升时,滑轮匀速转动,处于杠杆平衡,F1L1=F2L2, L1=2L2 ,则 F1="1/2" F2,故动滑轮可省一半的力;
(2)要想比较 拉力大小是否与拉力方向有关,所以应改变F1方向,仍匀速拉动物体上升,比较F1大小是否改变.
考点:滑轮与杠杆
25. 小 省力 5×103kg 4×105J 8×103W
【详解】
(1)由杠杆的平衡条件F1L1=F2L2可得: ,由此可知当阻力臂和动力不变时,阻力与动力臂成正比,即动力臂越大,阻力越大;动力臂越小,阻力越小,故为保持平衡,起重臂的长度越短的塔式起重机,配备的平衡重的质量应越小;
(2)图示中滑轮a为动滑轮,其作用是省力,可以省一半的力;由题意可知该滑轮组承担总重的绳子有2段,故G=2F=2.5×104N×2=5×104N,由G=mg可得:=5×103kg;
(3) 钢丝绳做功:W=Fs=Gh=2×104N ×20m=4×105J,由于水平移动时,重力方向上没移动距离,故水平移动过程中钢丝绳没做功;
(4) 电动机的有用功:W有用=Gh=1.2×104N×30m=3.6×105J,电动机的总功: =4×105J,电动机的实际功率: =8000W.
26. 112 越大 尽量减小低头的角度(或不要长时间低头做事,低头时间久了要抬头休息等等)
【详解】
(1)由表格中数据知,当低头角度为30°时,若m=1kg,细线的拉力为14N;
若m=8kg,由于角度不变,所以动力臂和阻力臂不变,则拉力F=8×14N=112N;
(2)由题意知,细线拉力的方向应垂直于OB向下,如图所示:
(3)图乙中,F的力臂为OB,做出乙图中G的力臂LG,如图所示:
根据杠杆的平衡条件可得:G LG=F LF,则,人低头的角度越大,sinθ越大,则G的力臂越大,肌肉的拉力就越大;
(4)要预防和延缓颈椎损伤,可尽量减小低头的角度,不要长时间低头做事,低头时间久了要抬头休息等等.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第十一章 简单机械和功
- 1 杠杆
- 2 滑轮
- 3 功
- 4 功率
- 5 机械效率
- 第十二章 机械能和内能
- 1 动能 势能 机械能
- 2 内能 热传递
- 3 物质的比热容
- 4 机械能和内能的相互转化
- 第十三章 电路初探
- 1 初识家用电器和电路
- 2 电路连接的基本方式
- 3 电流和电流表的使用
- 4 电压和电压表的使用
- 第十四章 欧姆定律
- 1 电阻
- 2 变阻器
- 3 欧姆定律
- 4 欧姆定律的应用
- 第十五章 电功和电热
- 电能表与电功
- 电功率
- 电热器 电流的热效应
- 家庭电路与安全用电
- 第十六章 电磁转换
- 磁体与磁场
- 电流的磁场
- 磁场对电流的作用 电动机
- 安装直流电动机模型
- 电磁感应 发电机
- 第十七章 电磁波与现代通信
- 信息与信息传播
- 电磁波及其传播
- 现代通信 走进信息时代
- 第十八章 能源与可持续发展
- 能源利用与社会发展
- 核能
- 太阳能
- 能量转化的基本规律
- 能源与可持续发展
