四川省成都七中2012-2013学年高二下学期入学考试数学(文)试题
文档属性
| 名称 | 四川省成都七中2012-2013学年高二下学期入学考试数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 309.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-25 00:00:00 | ||
图片预览


文档简介
成都七中2012-2013学年下期
2014级入学考试数学试卷(文科)
一、选择题(每小题5分,共75分,在每小题给出的四个选项中,只有一项是符合要求的.)
1.已知则 ( )
(A) (B) (C) (D)
2.从六个数中任取两个不同数作积,则不同的积有( )个.
(A) (B) (C) (D)
3.已知椭圆的方程为,则此椭圆的离心率为( )
(A) (B) (C) (D)
4.某校高二年级15个班参加成都市调研考试的参考人数的茎叶图
如图,则这组数据的中位数和众数分别是( )
(A)和 (B)和 (C)和 (D)和
5.在四面体中,分别是的中点,若,且则
( )
(A) (B) (C) (D)
6.双曲线的焦距是( )
(A) (B)
(C) (D)
7.右侧的程序执行后的结果是( )
(A) (B)
(C) (D)
8.在面积为的内部任取一点,则的面积大于的概率是( )
(A) (B) (C) (D)
9.圆上有8个点,过每两个点画一条弦,一共可以画( )条弦.
(A) (B) (C) (D)
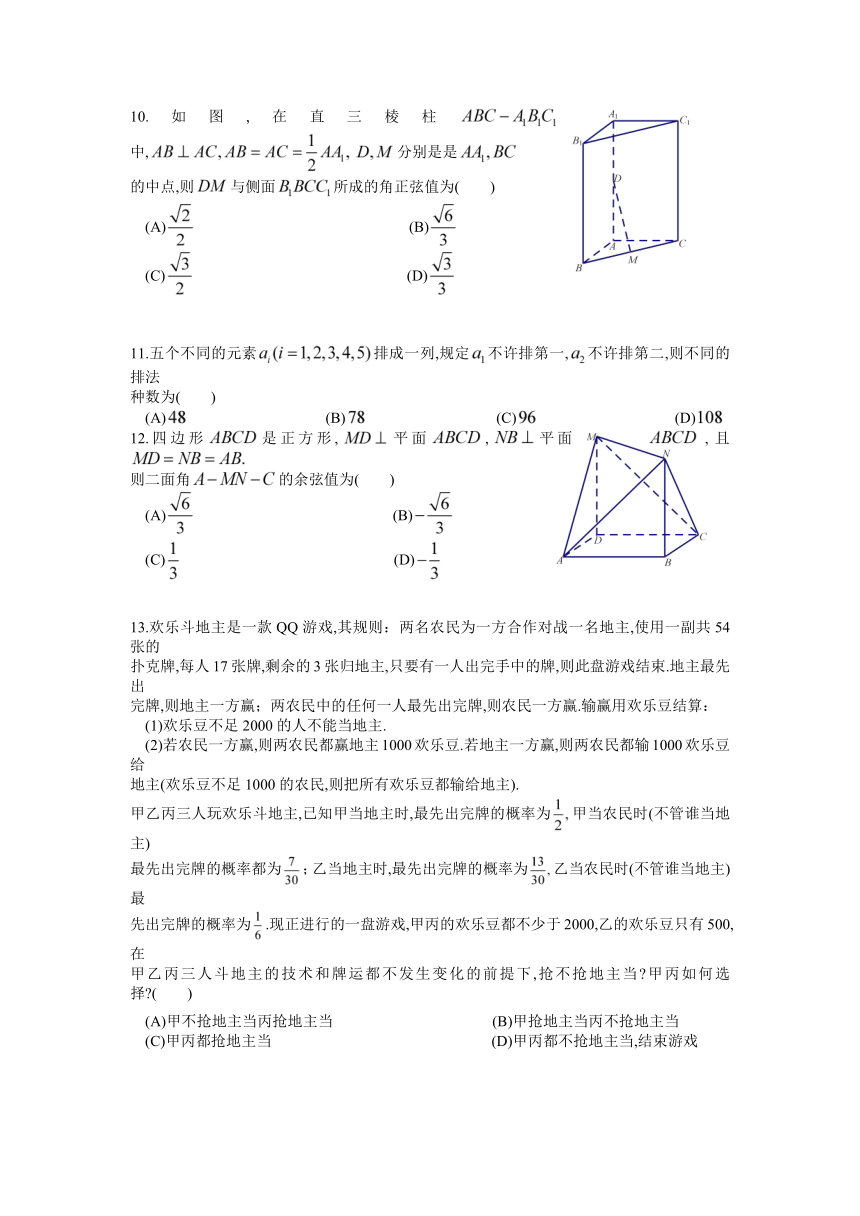
10.如图,在直三棱柱中,分别是是
的中点,则与侧面所成的角正弦值为( )
(A) (B)
(C) (D)
11.五个不同的元素排成一列,规定不许排第一,不许排第二,则不同的排法
种数为( )
(A) (B) (C) (D)
12.四边形是正方形,平面,平面,且
则二面角的余弦值为( )
(A) (B)
(C) (D)
13.欢乐斗地主是一款QQ游戏,其规则:两名农民为一方合作对战一名地主,使用一副共54张的
扑克牌,每人17张牌,剩余的3张归地主,只要有一人出完手中的牌,则此盘游戏结束.地主最先出
完牌,则地主一方赢;两农民中的任何一人最先出完牌,则农民一方赢.输赢用欢乐豆结算:
(1)欢乐豆不足2000的人不能当地主.
(2)若农民一方赢,则两农民都赢地主1000欢乐豆.若地主一方赢,则两农民都输1000欢乐豆给
地主(欢乐豆不足1000的农民,则把所有欢乐豆都输给地主).
甲乙丙三人玩欢乐斗地主,已知甲当地主时,最先出完牌的概率为甲当农民时(不管谁当地主)
最先出完牌的概率都为;乙当地主时,最先出完牌的概率为乙当农民时(不管谁当地主)最
先出完牌的概率为.现正进行的一盘游戏,甲丙的欢乐豆都不少于2000,乙的欢乐豆只有500,在
甲乙丙三人斗地主的技术和牌运都不发生变化的前提下,抢不抢地主当?甲丙如何选择?( )
(A)甲不抢地主当丙抢地主当 (B)甲抢地主当丙不抢地主当
(C)甲丙都抢地主当 (D)甲丙都不抢地主当,结束游戏
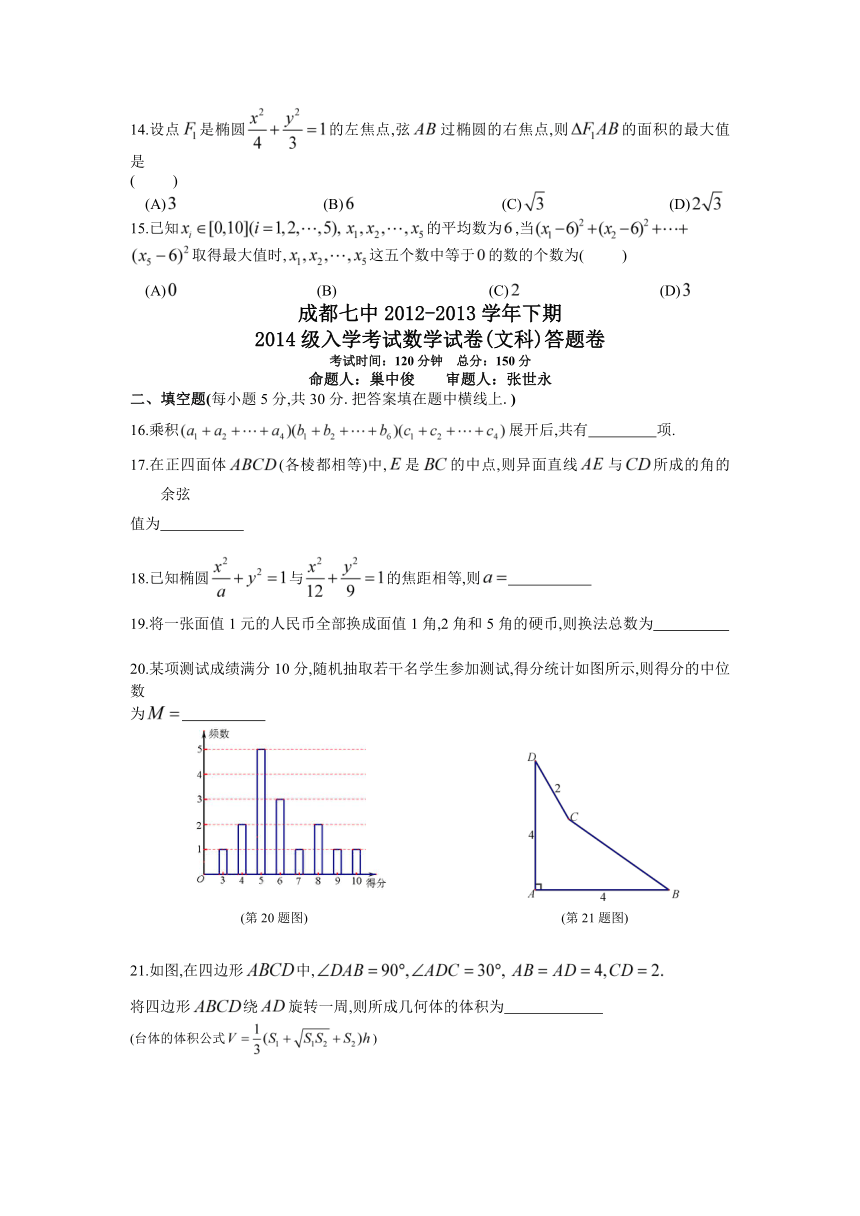
14.设点是椭圆的左焦点,弦过椭圆的右焦点,则的面积的最大值是
( )
(A) (B) (C) (D)
15.已知的平均数为,当
取得最大值时,这五个数中等于的数的个数为( )
(A) (B) (C) (D)
成都七中2012-2013学年下期
2014级入学考试数学试卷(文科)答题卷
考试时间:120分钟 总分:150分
命题人:巢中俊 审题人:张世永
二、填空题(每小题5分,共30分.把答案填在题中横线上.)
16.乘积展开后,共有 项.
17.在正四面体(各棱都相等)中,是的中点,则异面直线与所成的角的余弦
值为
18.已知椭圆与的焦距相等,则
19.将一张面值1元的人民币全部换成面值1角,2角和5角的硬币,则换法总数为
20.某项测试成绩满分10分,随机抽取若干名学生参加测试,得分统计如图所示,则得分的中位数
为
(第20题图) (第21题图)
21.如图,在四边形中,
将四边形绕旋转一周,则所成几何体的体积为
(台体的体积公式)
三、解答题(每小题15分,共45分.解答应写出文字说明、证明过程或演算步骤.)
22. (1)甲、乙、丙三人排成一排照相留念,求所有排列的方法种数.
(2)以正方体的顶点为顶点,可以确定多少个四棱锥?
(3)黑暗中从3双尺码不同的鞋子中任意摸出2只,求摸出2只不能配成一双(事件)的概率..
23.已知中,,分别是的中点,将沿
着翻折成使得平面平面,是上的一点且满足
(1)证明:平面.
(2)求三棱锥的体积.
(3)求异面直线与所成角的正切值.
24.已知圆圆点为坐标原点,点是圆上的一动点,线
段交圆于过点作轴的垂线交轴于,过点作的垂线交于
(1)当动点在圆上运动时,求点的轨迹的方程.
(2)设直线与轨迹交于不同的两点,求实数的取值范围.
(3)当时,直线与轨迹相交于两点,
求的面积.
成都七中2012-2013学年下期
2014级入学考试数学试卷(文科)试卷参考答案
一、选择题(每小题5分,共75分,在每小题给出的四个选项中,只有一项是符合要求的.)
C B A C D D B A B D B C A A C
14.设直线的方程为,联立消得.
设.则.
令则,在上递增,所以,达到最小值
15.这五个数的方差
所以取得最大值等价于方差最大.
这五个数越偏离平均数,方差越大.即极端值越多,方差越大.所以尽可能多.
假设个数都取或,设有个,则有个.
则,解得,
二、填空题(每小题5分,共30分.把答案填在题中横线上.)
16. 17. 18.
19. 20. 21.
三、解答题(每小题15分,共45分.解答应写出文字说明、证明过程或演算步骤.)
22.解(1) …………分
(2) …………分
(3). …………分
23.解(1)证明:连接交于连接分别是的中点,
. 又
从而在中,,
所以. …………分
平面.
…………分
(2)
…………分
(3)过作交的延长线于连接
异面直线与所成角就是或其补角.
四边形是边长为2的正方形.所以.
.
所以,在中,
异面直线与所成角的正切值为. …………分
注:采用建系也可.
24.解(1)设点.则.从而
因为,所以.即所以.
点在圆上,所以.整理得点的轨迹的方程:
…………分
(2)联立消得到. …………分
因为直线与轨迹交于不同的两点,所以
即所以实数的取值范围为 …………分
(3)(方法1)直线设,
联立消得到.则
直线设到直线的距离为则
…………分
(方法2)直线设直线与轴交于点,则.
设,
则
联立消得到.则
所以 …………分
2014级入学考试数学试卷(文科)
一、选择题(每小题5分,共75分,在每小题给出的四个选项中,只有一项是符合要求的.)
1.已知则 ( )
(A) (B) (C) (D)
2.从六个数中任取两个不同数作积,则不同的积有( )个.
(A) (B) (C) (D)
3.已知椭圆的方程为,则此椭圆的离心率为( )
(A) (B) (C) (D)
4.某校高二年级15个班参加成都市调研考试的参考人数的茎叶图
如图,则这组数据的中位数和众数分别是( )
(A)和 (B)和 (C)和 (D)和
5.在四面体中,分别是的中点,若,且则
( )
(A) (B) (C) (D)
6.双曲线的焦距是( )
(A) (B)
(C) (D)
7.右侧的程序执行后的结果是( )
(A) (B)
(C) (D)
8.在面积为的内部任取一点,则的面积大于的概率是( )
(A) (B) (C) (D)
9.圆上有8个点,过每两个点画一条弦,一共可以画( )条弦.
(A) (B) (C) (D)
10.如图,在直三棱柱中,分别是是
的中点,则与侧面所成的角正弦值为( )
(A) (B)
(C) (D)
11.五个不同的元素排成一列,规定不许排第一,不许排第二,则不同的排法
种数为( )
(A) (B) (C) (D)
12.四边形是正方形,平面,平面,且
则二面角的余弦值为( )
(A) (B)
(C) (D)
13.欢乐斗地主是一款QQ游戏,其规则:两名农民为一方合作对战一名地主,使用一副共54张的
扑克牌,每人17张牌,剩余的3张归地主,只要有一人出完手中的牌,则此盘游戏结束.地主最先出
完牌,则地主一方赢;两农民中的任何一人最先出完牌,则农民一方赢.输赢用欢乐豆结算:
(1)欢乐豆不足2000的人不能当地主.
(2)若农民一方赢,则两农民都赢地主1000欢乐豆.若地主一方赢,则两农民都输1000欢乐豆给
地主(欢乐豆不足1000的农民,则把所有欢乐豆都输给地主).
甲乙丙三人玩欢乐斗地主,已知甲当地主时,最先出完牌的概率为甲当农民时(不管谁当地主)
最先出完牌的概率都为;乙当地主时,最先出完牌的概率为乙当农民时(不管谁当地主)最
先出完牌的概率为.现正进行的一盘游戏,甲丙的欢乐豆都不少于2000,乙的欢乐豆只有500,在
甲乙丙三人斗地主的技术和牌运都不发生变化的前提下,抢不抢地主当?甲丙如何选择?( )
(A)甲不抢地主当丙抢地主当 (B)甲抢地主当丙不抢地主当
(C)甲丙都抢地主当 (D)甲丙都不抢地主当,结束游戏
14.设点是椭圆的左焦点,弦过椭圆的右焦点,则的面积的最大值是
( )
(A) (B) (C) (D)
15.已知的平均数为,当
取得最大值时,这五个数中等于的数的个数为( )
(A) (B) (C) (D)
成都七中2012-2013学年下期
2014级入学考试数学试卷(文科)答题卷
考试时间:120分钟 总分:150分
命题人:巢中俊 审题人:张世永
二、填空题(每小题5分,共30分.把答案填在题中横线上.)
16.乘积展开后,共有 项.
17.在正四面体(各棱都相等)中,是的中点,则异面直线与所成的角的余弦
值为
18.已知椭圆与的焦距相等,则
19.将一张面值1元的人民币全部换成面值1角,2角和5角的硬币,则换法总数为
20.某项测试成绩满分10分,随机抽取若干名学生参加测试,得分统计如图所示,则得分的中位数
为
(第20题图) (第21题图)
21.如图,在四边形中,
将四边形绕旋转一周,则所成几何体的体积为
(台体的体积公式)
三、解答题(每小题15分,共45分.解答应写出文字说明、证明过程或演算步骤.)
22. (1)甲、乙、丙三人排成一排照相留念,求所有排列的方法种数.
(2)以正方体的顶点为顶点,可以确定多少个四棱锥?
(3)黑暗中从3双尺码不同的鞋子中任意摸出2只,求摸出2只不能配成一双(事件)的概率..
23.已知中,,分别是的中点,将沿
着翻折成使得平面平面,是上的一点且满足
(1)证明:平面.
(2)求三棱锥的体积.
(3)求异面直线与所成角的正切值.
24.已知圆圆点为坐标原点,点是圆上的一动点,线
段交圆于过点作轴的垂线交轴于,过点作的垂线交于
(1)当动点在圆上运动时,求点的轨迹的方程.
(2)设直线与轨迹交于不同的两点,求实数的取值范围.
(3)当时,直线与轨迹相交于两点,
求的面积.
成都七中2012-2013学年下期
2014级入学考试数学试卷(文科)试卷参考答案
一、选择题(每小题5分,共75分,在每小题给出的四个选项中,只有一项是符合要求的.)
C B A C D D B A B D B C A A C
14.设直线的方程为,联立消得.
设.则.
令则,在上递增,所以,达到最小值
15.这五个数的方差
所以取得最大值等价于方差最大.
这五个数越偏离平均数,方差越大.即极端值越多,方差越大.所以尽可能多.
假设个数都取或,设有个,则有个.
则,解得,
二、填空题(每小题5分,共30分.把答案填在题中横线上.)
16. 17. 18.
19. 20. 21.
三、解答题(每小题15分,共45分.解答应写出文字说明、证明过程或演算步骤.)
22.解(1) …………分
(2) …………分
(3). …………分
23.解(1)证明:连接交于连接分别是的中点,
. 又
从而在中,,
所以. …………分
平面.
…………分
(2)
…………分
(3)过作交的延长线于连接
异面直线与所成角就是或其补角.
四边形是边长为2的正方形.所以.
.
所以,在中,
异面直线与所成角的正切值为. …………分
注:采用建系也可.
24.解(1)设点.则.从而
因为,所以.即所以.
点在圆上,所以.整理得点的轨迹的方程:
…………分
(2)联立消得到. …………分
因为直线与轨迹交于不同的两点,所以
即所以实数的取值范围为 …………分
(3)(方法1)直线设,
联立消得到.则
直线设到直线的距离为则
…………分
(方法2)直线设直线与轴交于点,则.
设,
则
联立消得到.则
所以 …………分
同课章节目录
