华东师大版八下数学16.1 分式及其基本性质(共19张PPT)
文档属性
| 名称 | 华东师大版八下数学16.1 分式及其基本性质(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 539.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-16 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
课题,分式
科目,数学
年级,八年级下
教材版本,华东师大版
第16章 分式
1 分式及其基本性质
1 分式
2.能熟练地求出分式有意义、无意义及分式值为零的条件.
1.理解分式的概念.
1.长方形的面积为10cm ,长为7cm,宽应为____cm;
长方形的面积为S,长为a,宽应为______.
S
a
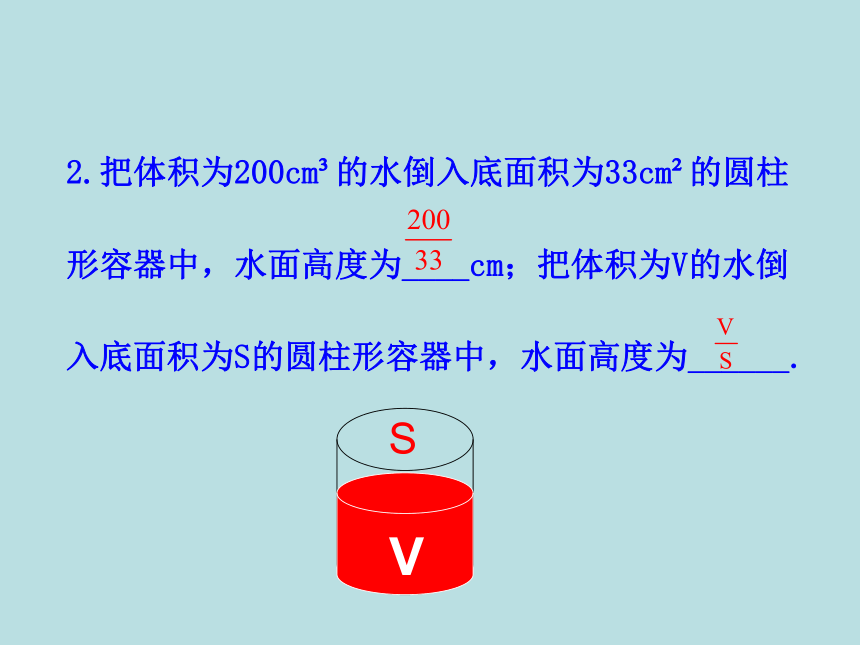
2.把体积为200cm 的水倒入底面积为33cm 的圆柱
形容器中,水面高度为____cm;把体积为V的水倒
入底面积为S的圆柱形容器中,水面高度为______.
V
S
形如 (A,B是整式,且B中含有字母,
B≠0)的式子,叫做分式.其中A叫做分式的分
子,B叫做分式的分母.
概念
下列各式中,哪些是整式?哪些是分式?
指出下列代数式中,哪些是整式,哪些是分式?
【解析】整式有
分式有
【例题】
1.分式 的分母有什么条件限制
当B=0时,分式 无意义.
当B≠0时,分式 有意义.
2.当 =0时分子和分母应满足什么条件?
当A=0且B≠0时,分式 的值为零.
(1)当x 时,分式 有意义;
(2)当x 时,分式 有意义;
解:分母 3x≠0 即 x≠0
答案:≠0
解:分母 x-1≠0 即 x≠1
答案:≠1
【例题】
(3)当b 时,分式 有意义;
(4)当x,y 满足关系 时,分式 有意义.
解:分母 x-y≠0 即 x≠y
答案:x≠y
解:分母 5-3b≠0 即 b≠
答案:≠
(2) 当x为何值时,分式有意义
(1) 当x为何值时,分式无意义
已知分式 ,
(2)当x ≠-2时,分式有意义.
∴当x = -2时分式
解:(1)当分母等于零时,分式无意义.
无意义.
∴ x =-2,
即 x+2=0
【跟踪训练】
当 时,分式 的值为零.
答案:x=1
【解析】要使分式的值为零,只需分子为零且分母不为零,
∴
解得x=1.
【例题】
【解析】选B.
由x2-1=0得x2=1,
∴x=±1, 又∵x-1≠0即x≠1, ∴x=-1.
(荆州·中考)若分式 的值为0,则( )
A.x=1 B.x=-1 C.x=±1 D.x≠1
【跟踪训练】
【解析】选A.由题意得x-2≠0,解得x≠2,
1.若分式 有意义,则( )
A.x≠2 B.x≠-3
C.x≠-3或x≠2 D.无法确定
2.(江津·中考)下列式子是分式的是( )
【解析】选B.根据分式的定义判断,A,C分母中都不含有字母,D中虽含有字母π,但是其表示一个固定的数——圆周率.
A. B. C. D.
3.(枣庄·中考)若 的值为零,则x= .
【解析】分式的值等于零,应满足分子等于零,同时
分母不为零,即
解得
答案:-3
通过本课时的学习,需要我们
1.知道分式的概念,会辨别分式与整式.
2.会求分式有意义时字母的取值范围.
3.会求分式值为零时的字母的取值.
再长的路,一步步也能走完,再短的路,不迈开双脚也无法到达。
课题,分式
科目,数学
年级,八年级下
教材版本,华东师大版
第16章 分式
1 分式及其基本性质
1 分式
2.能熟练地求出分式有意义、无意义及分式值为零的条件.
1.理解分式的概念.
1.长方形的面积为10cm ,长为7cm,宽应为____cm;
长方形的面积为S,长为a,宽应为______.
S
a
2.把体积为200cm 的水倒入底面积为33cm 的圆柱
形容器中,水面高度为____cm;把体积为V的水倒
入底面积为S的圆柱形容器中,水面高度为______.
V
S
形如 (A,B是整式,且B中含有字母,
B≠0)的式子,叫做分式.其中A叫做分式的分
子,B叫做分式的分母.
概念
下列各式中,哪些是整式?哪些是分式?
指出下列代数式中,哪些是整式,哪些是分式?
【解析】整式有
分式有
【例题】
1.分式 的分母有什么条件限制
当B=0时,分式 无意义.
当B≠0时,分式 有意义.
2.当 =0时分子和分母应满足什么条件?
当A=0且B≠0时,分式 的值为零.
(1)当x 时,分式 有意义;
(2)当x 时,分式 有意义;
解:分母 3x≠0 即 x≠0
答案:≠0
解:分母 x-1≠0 即 x≠1
答案:≠1
【例题】
(3)当b 时,分式 有意义;
(4)当x,y 满足关系 时,分式 有意义.
解:分母 x-y≠0 即 x≠y
答案:x≠y
解:分母 5-3b≠0 即 b≠
答案:≠
(2) 当x为何值时,分式有意义
(1) 当x为何值时,分式无意义
已知分式 ,
(2)当x ≠-2时,分式有意义.
∴当x = -2时分式
解:(1)当分母等于零时,分式无意义.
无意义.
∴ x =-2,
即 x+2=0
【跟踪训练】
当 时,分式 的值为零.
答案:x=1
【解析】要使分式的值为零,只需分子为零且分母不为零,
∴
解得x=1.
【例题】
【解析】选B.
由x2-1=0得x2=1,
∴x=±1, 又∵x-1≠0即x≠1, ∴x=-1.
(荆州·中考)若分式 的值为0,则( )
A.x=1 B.x=-1 C.x=±1 D.x≠1
【跟踪训练】
【解析】选A.由题意得x-2≠0,解得x≠2,
1.若分式 有意义,则( )
A.x≠2 B.x≠-3
C.x≠-3或x≠2 D.无法确定
2.(江津·中考)下列式子是分式的是( )
【解析】选B.根据分式的定义判断,A,C分母中都不含有字母,D中虽含有字母π,但是其表示一个固定的数——圆周率.
A. B. C. D.
3.(枣庄·中考)若 的值为零,则x= .
【解析】分式的值等于零,应满足分子等于零,同时
分母不为零,即
解得
答案:-3
通过本课时的学习,需要我们
1.知道分式的概念,会辨别分式与整式.
2.会求分式有意义时字母的取值范围.
3.会求分式值为零时的字母的取值.
再长的路,一步步也能走完,再短的路,不迈开双脚也无法到达。
