华东师大版八下数学19.2.1菱形的性质 课件(24张ppt)
文档属性
| 名称 | 华东师大版八下数学19.2.1菱形的性质 课件(24张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 592.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-17 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
菱形的性质
平行四边形的性质
边
平行四边形的对边平行且相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
温故知新
矩形的性质
矩形的四个角都是直角
矩形的对角线相等且互相平分
上图你熟悉吗?你在现实的生活中看见过吗?
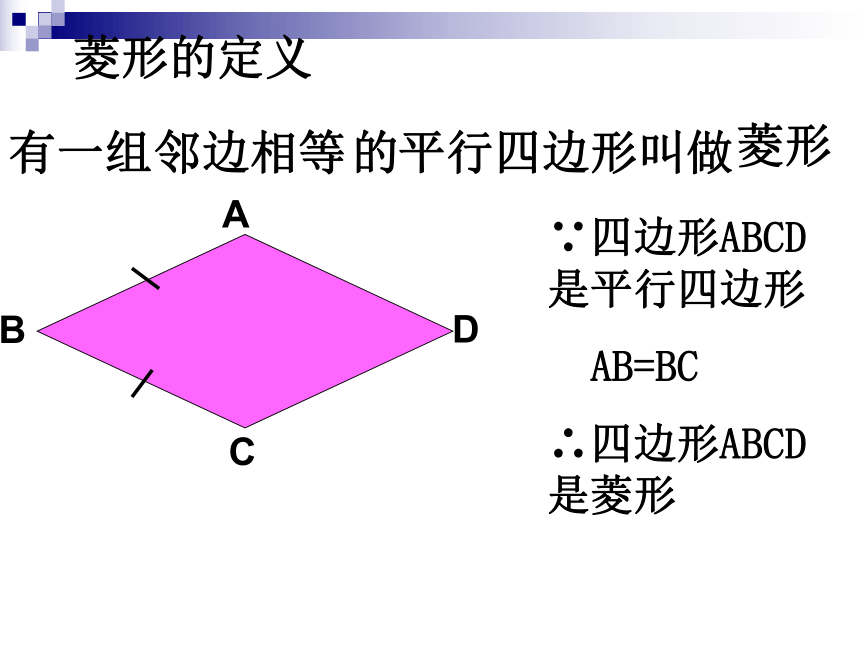
有一组 的 叫做
邻边相等
平行四边形
A
D
C
B
∵四边形ABCD是平行四边形
AB=BC
∴四边形ABCD是菱形
菱形
菱形的定义
如图,在菱形ABCD中,对角线AC、BD相交于点O.
⑴图中有哪些线段是相等的?
⑵图中对角线AC,BD有什么特定的位置关系?
解:AB=BC=CD=DA
AO=CO
DO=BO
解:AC⊥BD, AC平分∠DAB 和∠DCB,
BD平分∠ADC 和∠ABC.
A
B
C
D
O
如图,在菱形ABCD中,对角线AC、BD相交于点O.
⑶图中有哪些等腰三角形、直角三角形?
解:等腰三角形:
△ABD,△CBD,△ACD,△ABC
直角三角形:
Rt△ADO,Rt△AOB Rt△DOC,Rt△BOC
A
B
C
D
O
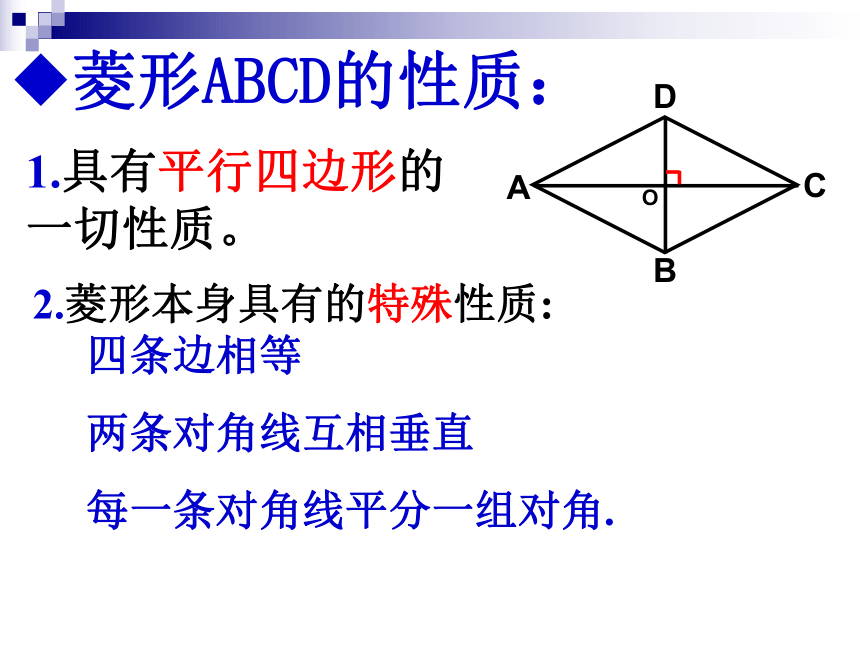
菱形ABCD的性质:
1.具有平行四边形的一切性质。
2.菱形本身具有的特殊性质:
四条边相等
两条对角线互相垂直
每一条对角线平分一组对角.
A
B
C
D
O
3.菱形的对称性:
菱形是中心对称图形,对称中心为对角线的交点;也是轴对称图形,对称轴是对角线所在的直线(有两条对称轴)
例:在菱形ABCD中,∠BAD=2∠B,试求出∠B的度数,并说明△ABC是等边三角形。
A
B
C
D
解(1)在菱形ABCD中
∠B+∠BAD=180°
∵∠BAD=2∠B
∴∠B=60°
(2)在菱形ABCD中,
AB=BC
∴∠BAC=∠BCA
又∵∠B+∠BAC+∠BCA=180°
且∠B=60°
∴∠BAC=∠BCA=∠B=60°
∴AB=BC=AC
即△ABC是等边三角形。
A
B
C
D
∵AC=8,BD=6
= AC·(BO+DO)
例:如图,已知菱形ABCD中,对角线AC=8cm,BD=6cm,请你求出这个菱形的面积和周长。
解:
在菱形ABCD中,
AC⊥BD,BO=DO
∴S菱形ABCD=S△ABC+ S△ADC
= AC·BO+ AC·DO
S菱形= a·b(a、b为对角线长)
∴S菱形ABCD= ×8×6=24cm2
菱形的面积等于两条对角线长的乘积的一半。
2
1
2
1
2
1
= AC·BD
2
1
2
1
2
1
A
D
C
B
O
(菱形的对角线互相垂直平分)
菱形的面积公式
C
B
D
A
O
E
辨别对错
1.有一组邻边相等的四边形是菱形. ( )
2.菱形是平行四边形.( )
打好基础:
比一比,看谁的反应最快!
1、菱形具有而矩形不一定具有的性质是( )
A、一组对边平行,另一组对边相等
B、对角线互相垂直
C、对角线互相平分
D、对角相等且互补
2、对于以下图形(1)矩形(2)等边三角形(3)平行四边形(4)菱形(5)圆(6)线段, 既是轴对称图形又是中心对称图形的有( )
A、1个 B、2个 C、3个 D、4个
B
D
比一比,看谁反应最快
5、已知菱形的两条对角线长分别是10和 24,则菱形的周长为_____。
3、已知菱形的周长是16cm,则它的边长是_____cm
4、如图,菱形ABCD中∠BAC=30 ° ,则∠ABD=______________
A
D
C
B
O
6、已知菱形ABCD的周长是8cm,∠ABC=120 ,求对角线AC,BD的长及菱形的面积.
A
B
C
D
O
1.如图,在菱形ABCD中,E是AB的中点,DE⊥AB,AB=2。求:
⑴∠ABC的度数。
⑵菱形ABCD的面积。
推展提升:
B
A
D
C
E
2.已知菱形ABCD中,两相邻内角之比为1:3,高为2,求菱形的面积。
推展提升:
同学们,今天你有什么收获?
有一组邻边相等的平行四边形叫做菱形.
菱形的定义:
菱形的性质:
边
对角线
角
菱形的性质
菱形的两组对边分别平行
菱形的四条边都相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分,
每一条对角线平分一组对角。
菱形的面积等于底乘高或两条对角线长的乘积的一半。
菱形是中心对称图形,对称中心是对角线的交点;也是轴对称图形,对称轴是对角线所在的直线(有两条对称轴)
菱形的对称性
作业:
112页 练习 1 3
谢谢大家
菱形的性质
平行四边形的性质
边
平行四边形的对边平行且相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
温故知新
矩形的性质
矩形的四个角都是直角
矩形的对角线相等且互相平分
上图你熟悉吗?你在现实的生活中看见过吗?
有一组 的 叫做
邻边相等
平行四边形
A
D
C
B
∵四边形ABCD是平行四边形
AB=BC
∴四边形ABCD是菱形
菱形
菱形的定义
如图,在菱形ABCD中,对角线AC、BD相交于点O.
⑴图中有哪些线段是相等的?
⑵图中对角线AC,BD有什么特定的位置关系?
解:AB=BC=CD=DA
AO=CO
DO=BO
解:AC⊥BD, AC平分∠DAB 和∠DCB,
BD平分∠ADC 和∠ABC.
A
B
C
D
O
如图,在菱形ABCD中,对角线AC、BD相交于点O.
⑶图中有哪些等腰三角形、直角三角形?
解:等腰三角形:
△ABD,△CBD,△ACD,△ABC
直角三角形:
Rt△ADO,Rt△AOB Rt△DOC,Rt△BOC
A
B
C
D
O
菱形ABCD的性质:
1.具有平行四边形的一切性质。
2.菱形本身具有的特殊性质:
四条边相等
两条对角线互相垂直
每一条对角线平分一组对角.
A
B
C
D
O
3.菱形的对称性:
菱形是中心对称图形,对称中心为对角线的交点;也是轴对称图形,对称轴是对角线所在的直线(有两条对称轴)
例:在菱形ABCD中,∠BAD=2∠B,试求出∠B的度数,并说明△ABC是等边三角形。
A
B
C
D
解(1)在菱形ABCD中
∠B+∠BAD=180°
∵∠BAD=2∠B
∴∠B=60°
(2)在菱形ABCD中,
AB=BC
∴∠BAC=∠BCA
又∵∠B+∠BAC+∠BCA=180°
且∠B=60°
∴∠BAC=∠BCA=∠B=60°
∴AB=BC=AC
即△ABC是等边三角形。
A
B
C
D
∵AC=8,BD=6
= AC·(BO+DO)
例:如图,已知菱形ABCD中,对角线AC=8cm,BD=6cm,请你求出这个菱形的面积和周长。
解:
在菱形ABCD中,
AC⊥BD,BO=DO
∴S菱形ABCD=S△ABC+ S△ADC
= AC·BO+ AC·DO
S菱形= a·b(a、b为对角线长)
∴S菱形ABCD= ×8×6=24cm2
菱形的面积等于两条对角线长的乘积的一半。
2
1
2
1
2
1
= AC·BD
2
1
2
1
2
1
A
D
C
B
O
(菱形的对角线互相垂直平分)
菱形的面积公式
C
B
D
A
O
E
辨别对错
1.有一组邻边相等的四边形是菱形. ( )
2.菱形是平行四边形.( )
打好基础:
比一比,看谁的反应最快!
1、菱形具有而矩形不一定具有的性质是( )
A、一组对边平行,另一组对边相等
B、对角线互相垂直
C、对角线互相平分
D、对角相等且互补
2、对于以下图形(1)矩形(2)等边三角形(3)平行四边形(4)菱形(5)圆(6)线段, 既是轴对称图形又是中心对称图形的有( )
A、1个 B、2个 C、3个 D、4个
B
D
比一比,看谁反应最快
5、已知菱形的两条对角线长分别是10和 24,则菱形的周长为_____。
3、已知菱形的周长是16cm,则它的边长是_____cm
4、如图,菱形ABCD中∠BAC=30 ° ,则∠ABD=______________
A
D
C
B
O
6、已知菱形ABCD的周长是8cm,∠ABC=120 ,求对角线AC,BD的长及菱形的面积.
A
B
C
D
O
1.如图,在菱形ABCD中,E是AB的中点,DE⊥AB,AB=2。求:
⑴∠ABC的度数。
⑵菱形ABCD的面积。
推展提升:
B
A
D
C
E
2.已知菱形ABCD中,两相邻内角之比为1:3,高为2,求菱形的面积。
推展提升:
同学们,今天你有什么收获?
有一组邻边相等的平行四边形叫做菱形.
菱形的定义:
菱形的性质:
边
对角线
角
菱形的性质
菱形的两组对边分别平行
菱形的四条边都相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分,
每一条对角线平分一组对角。
菱形的面积等于底乘高或两条对角线长的乘积的一半。
菱形是中心对称图形,对称中心是对角线的交点;也是轴对称图形,对称轴是对角线所在的直线(有两条对称轴)
菱形的对称性
作业:
112页 练习 1 3
谢谢大家
