人教版六年级下学期数学立体图形的整理复习课件(28张ppt)
文档属性
| 名称 | 人教版六年级下学期数学立体图形的整理复习课件(28张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-16 10:41:11 | ||
图片预览






文档简介
(共28张PPT)
六年级数学下册整理复习
立体图形复习
点动成线
线动成面
面动成体
1、回顾整理立体图形的特征、表面积、体积的含义和计算公式;理解体积的推导过程。
2、进一步探究立体图形之间的联系。
3、灵活运用公式解决实际问题。
复习目标:
群学要求:
1.把你掌握的立体图形的特征跟小组同学互相交流;比一比,看谁说得既有条理又具体。
2.对比一下,想想它们之间有什么相同点、区别和联系?
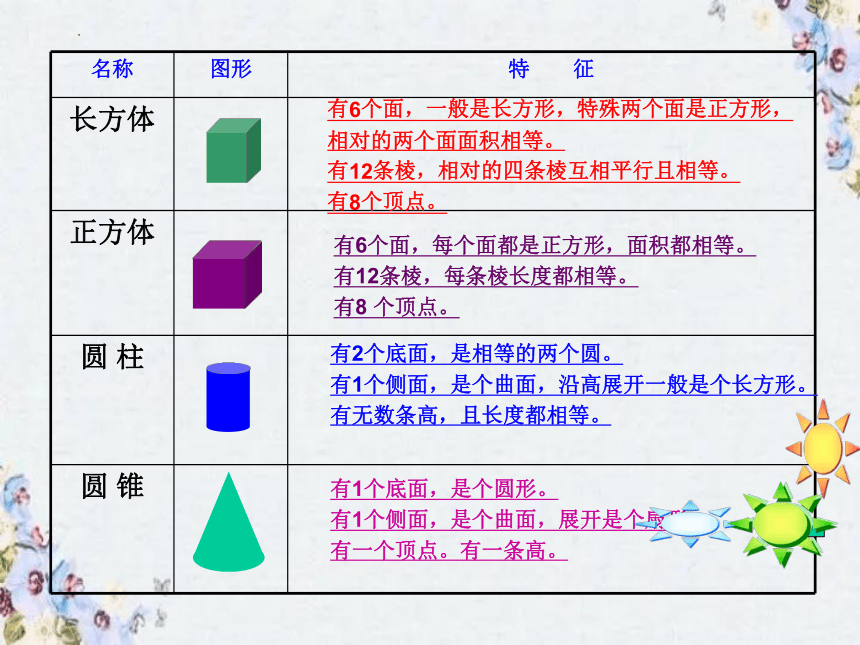
名称 图形 特 征
长方体
正方体
圆 柱
圆 锥
有6个面,一般是长方形,特殊两个面是正方形,
相对的两个面面积相等。
有12条棱,相对的四条棱互相平行且相等。
有8个顶点。
有6个面,每个面都是正方形,面积都相等。
有12条棱,每条棱长度都相等。
有8 个顶点。
有2个底面,是相等的两个圆。
有1个侧面,是个曲面,沿高展开一般是个长方形。
有无数条高,且长度都相等。
有1个底面,是个圆形。
有1个侧面,是个曲面,展开是个扇形。
有一个顶点。有一条高。
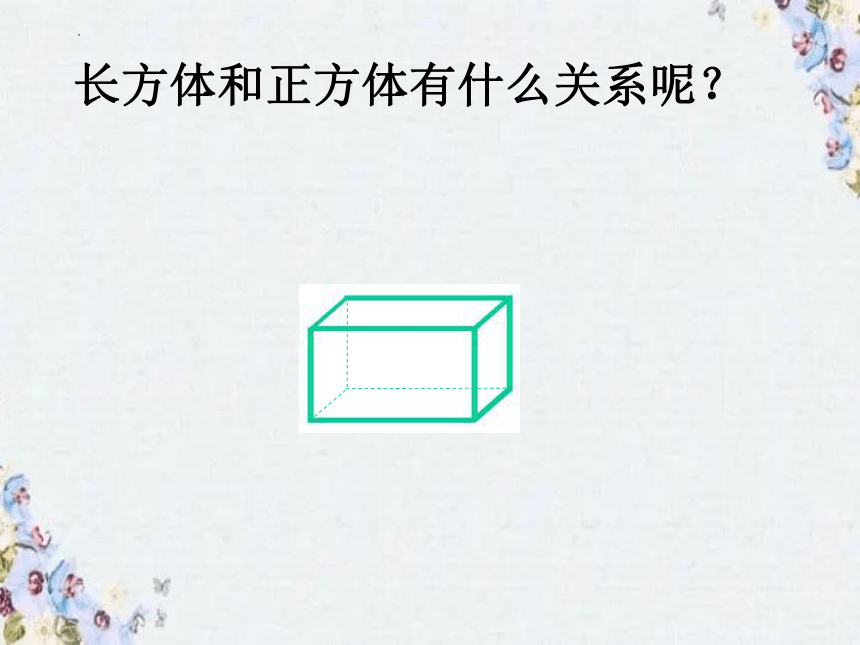
长方体和正方体有什么关系呢?
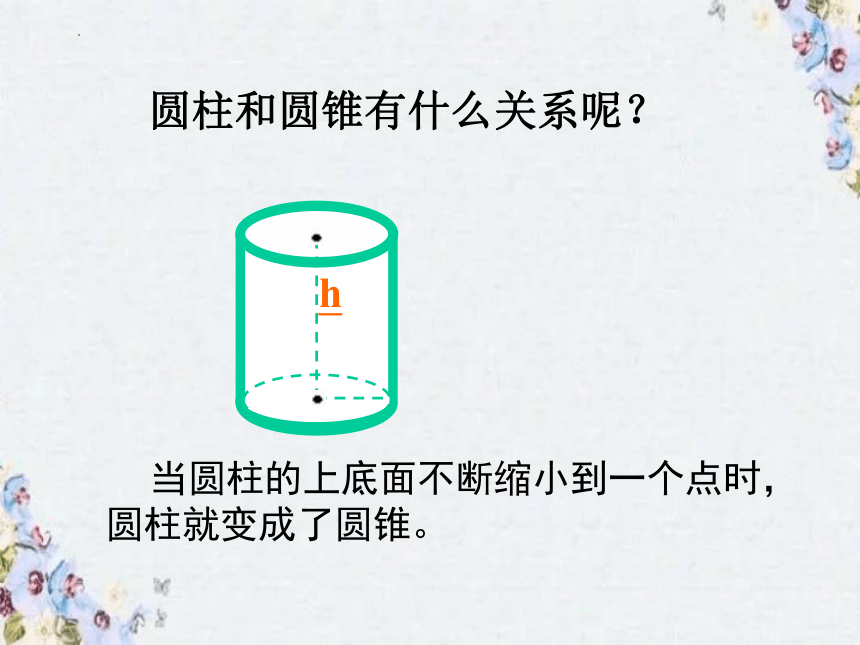
圆柱和圆锥有什么关系呢?
当圆柱的上底面不断缩小到一个点时,圆柱就变成了圆锥。
h
一个立体图形所有面的面积总和叫做它的表面积。
表面积:
a
b
h
a
a
a
h
r
长方体表面积=
正方体表面积=
圆柱侧面积=
圆柱表面积=
2(ab+ah+bh)
6a
=2лrh
2лrh+ 2лr
2
2
Ch
你能否找一个共同的方法来计算他们的表面积?
侧面积+2个底面积
什么是立体图形的体积?
一个立体图形所占空间的大小叫做它的体积。
V=
V=
V=
V=
abh
a
3
sh
1
3
sh
V = sh
正方体、长方体和圆柱的体积计算有什么相似的地方呢?
h
a
b
a
a
a
s
h
s
h
h
a
b
a
a
a
s
h
s
h
因为长方体的体积=底面积×高
底面
h
h
r
r
兀r
V = 兀r × h
2
所以圆柱的体积 = 底面积×高
V = S h
圆柱体积=底面积 高
1
3
圆锥体积=
底面积 高
等底等高的:
想一想:这些立体图形的体积的大小跟什么有关系呢?
圆柱、圆锥和我们学过的什么平面图形有关系呢?
生活中的数学
一、明察秋毫我会辨
① 一个长方体最多有两个正方形。( )
② 圆柱的侧面展开不是正方形就是长方形。
( )
③ 长方体的三条棱就是它的长、宽、高。
( )
④ 圆柱的体积是圆锥的体积的3倍。
( )
√
×
×
×
(1)做一个长方体铁皮罐头盒,求需要多少铁皮,是求它的( ),罐头盒周围贴商标纸,求商标纸的面积是求它的( )。
(2)做一只圆柱形通风管要用多少铁皮,是求它的( )。
(3) 一个圆柱形水池占地多少平方米,是求圆柱的( )。求水池占多大的空间就是求它的( )。求这个水池能装多少水是求它的( )。
表面积
侧面积
侧面积
底面积
二、认真思考我会填:
体积
容积
3、一个圆锥的体积是n立方厘米,和它等底等高的圆柱体的体积是( )立方厘米。
① n ②2n ③3n ④4n
4、等底等高的圆柱和圆锥的体积相差16立方米,这个圆柱的体积是( )立方米.
①12 ②9 ③27 ④24
1、正方体棱长3厘米,如果棱长扩大2倍,它的体积扩大( )倍?
①2 ②4 ③6 ④8
2、把一段长3米的长方体木料平均截成2 段,表面积增加8平方厘米,原来这段木料的体积是( )立方厘米。
①12 ②120 ③1200 ④2400
③
④
④
三、深思熟虑我会选:
③
你能推想一下下面的立体图形的体积可以怎样计算吗?
四、灵活运用我会算:
三角形
胜利集输小学 席海玲
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道的。
——毕达哥拉斯(古希腊数学家)
通过本节课的学习,你有什么收获?
谈一谈:
六年级数学下册整理复习
立体图形复习
点动成线
线动成面
面动成体
1、回顾整理立体图形的特征、表面积、体积的含义和计算公式;理解体积的推导过程。
2、进一步探究立体图形之间的联系。
3、灵活运用公式解决实际问题。
复习目标:
群学要求:
1.把你掌握的立体图形的特征跟小组同学互相交流;比一比,看谁说得既有条理又具体。
2.对比一下,想想它们之间有什么相同点、区别和联系?
名称 图形 特 征
长方体
正方体
圆 柱
圆 锥
有6个面,一般是长方形,特殊两个面是正方形,
相对的两个面面积相等。
有12条棱,相对的四条棱互相平行且相等。
有8个顶点。
有6个面,每个面都是正方形,面积都相等。
有12条棱,每条棱长度都相等。
有8 个顶点。
有2个底面,是相等的两个圆。
有1个侧面,是个曲面,沿高展开一般是个长方形。
有无数条高,且长度都相等。
有1个底面,是个圆形。
有1个侧面,是个曲面,展开是个扇形。
有一个顶点。有一条高。
长方体和正方体有什么关系呢?
圆柱和圆锥有什么关系呢?
当圆柱的上底面不断缩小到一个点时,圆柱就变成了圆锥。
h
一个立体图形所有面的面积总和叫做它的表面积。
表面积:
a
b
h
a
a
a
h
r
长方体表面积=
正方体表面积=
圆柱侧面积=
圆柱表面积=
2(ab+ah+bh)
6a
=2лrh
2лrh+ 2лr
2
2
Ch
你能否找一个共同的方法来计算他们的表面积?
侧面积+2个底面积
什么是立体图形的体积?
一个立体图形所占空间的大小叫做它的体积。
V=
V=
V=
V=
abh
a
3
sh
1
3
sh
V = sh
正方体、长方体和圆柱的体积计算有什么相似的地方呢?
h
a
b
a
a
a
s
h
s
h
h
a
b
a
a
a
s
h
s
h
因为长方体的体积=底面积×高
底面
h
h
r
r
兀r
V = 兀r × h
2
所以圆柱的体积 = 底面积×高
V = S h
圆柱体积=底面积 高
1
3
圆锥体积=
底面积 高
等底等高的:
想一想:这些立体图形的体积的大小跟什么有关系呢?
圆柱、圆锥和我们学过的什么平面图形有关系呢?
生活中的数学
一、明察秋毫我会辨
① 一个长方体最多有两个正方形。( )
② 圆柱的侧面展开不是正方形就是长方形。
( )
③ 长方体的三条棱就是它的长、宽、高。
( )
④ 圆柱的体积是圆锥的体积的3倍。
( )
√
×
×
×
(1)做一个长方体铁皮罐头盒,求需要多少铁皮,是求它的( ),罐头盒周围贴商标纸,求商标纸的面积是求它的( )。
(2)做一只圆柱形通风管要用多少铁皮,是求它的( )。
(3) 一个圆柱形水池占地多少平方米,是求圆柱的( )。求水池占多大的空间就是求它的( )。求这个水池能装多少水是求它的( )。
表面积
侧面积
侧面积
底面积
二、认真思考我会填:
体积
容积
3、一个圆锥的体积是n立方厘米,和它等底等高的圆柱体的体积是( )立方厘米。
① n ②2n ③3n ④4n
4、等底等高的圆柱和圆锥的体积相差16立方米,这个圆柱的体积是( )立方米.
①12 ②9 ③27 ④24
1、正方体棱长3厘米,如果棱长扩大2倍,它的体积扩大( )倍?
①2 ②4 ③6 ④8
2、把一段长3米的长方体木料平均截成2 段,表面积增加8平方厘米,原来这段木料的体积是( )立方厘米。
①12 ②120 ③1200 ④2400
③
④
④
三、深思熟虑我会选:
③
你能推想一下下面的立体图形的体积可以怎样计算吗?
四、灵活运用我会算:
三角形
胜利集输小学 席海玲
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道的。
——毕达哥拉斯(古希腊数学家)
通过本节课的学习,你有什么收获?
谈一谈:
