北师大版四年级下学期数学二 认识三角形和四边形2.4三角形边的关系课件(35张ppt)
文档属性
| 名称 | 北师大版四年级下学期数学二 认识三角形和四边形2.4三角形边的关系课件(35张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-16 10:54:29 | ||
图片预览




文档简介
(共35张PPT)
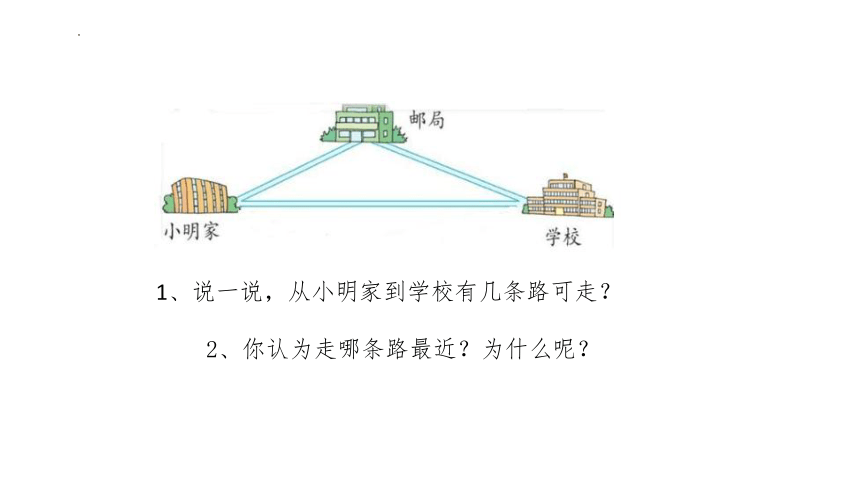
1、说一说,从小明家到学校有几条路可走?
2、你认为走哪条路最近?为什么呢?
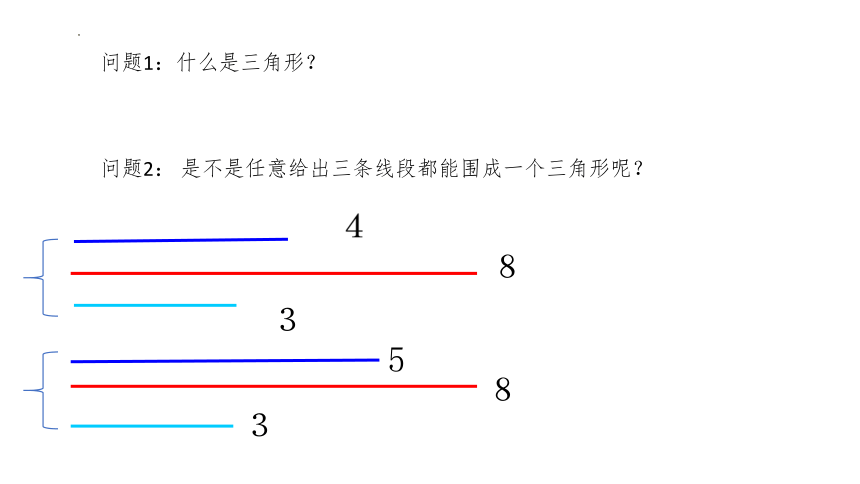
问题1:什么是三角形?
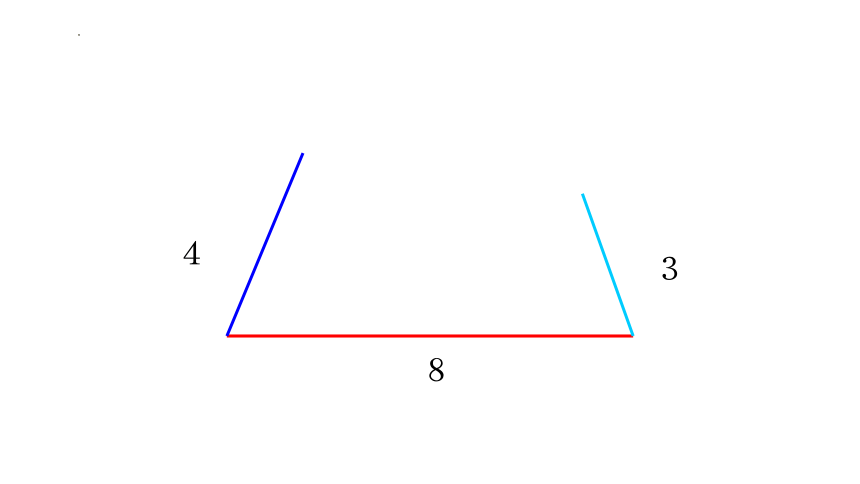
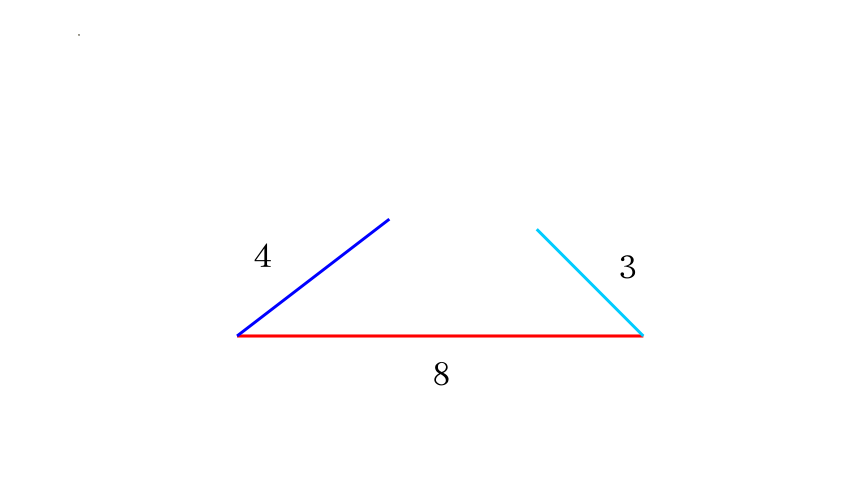
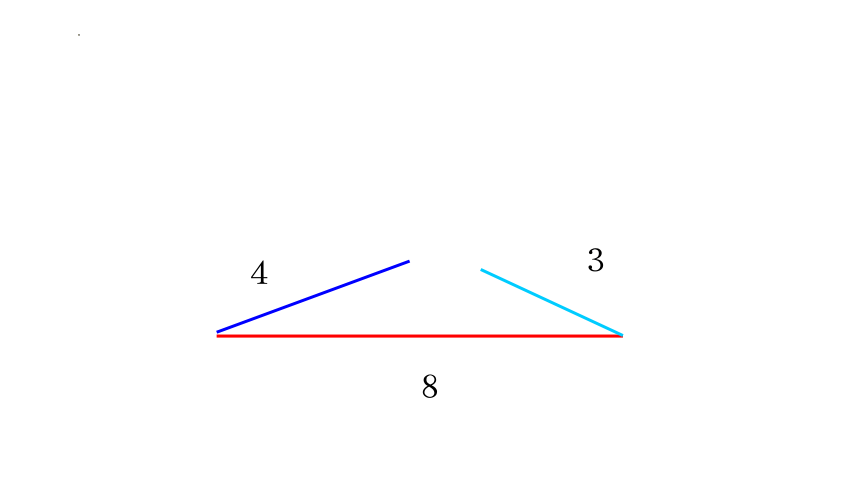
问题2: 是不是任意给出三条线段都能围成一个三角形呢?
8
3
8
3
5
4
8
3
探索
与
发现
4
8
3
4
8
3
4
8
3
4
8
3
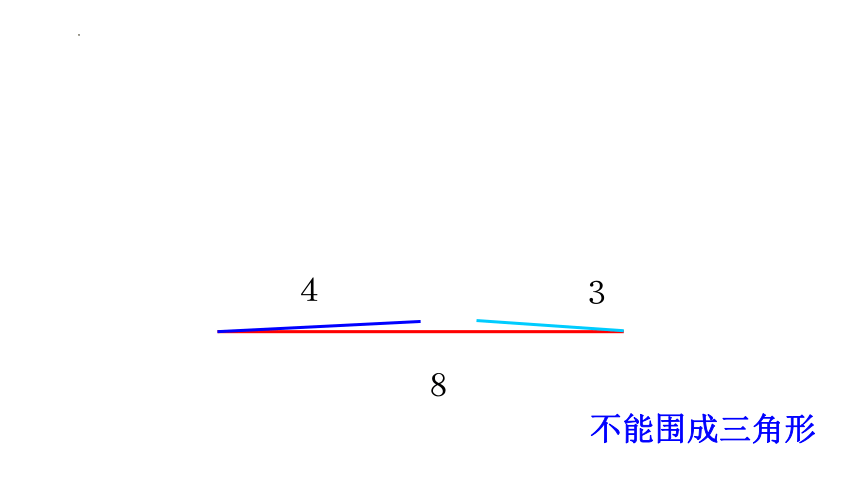
不能围成三角形
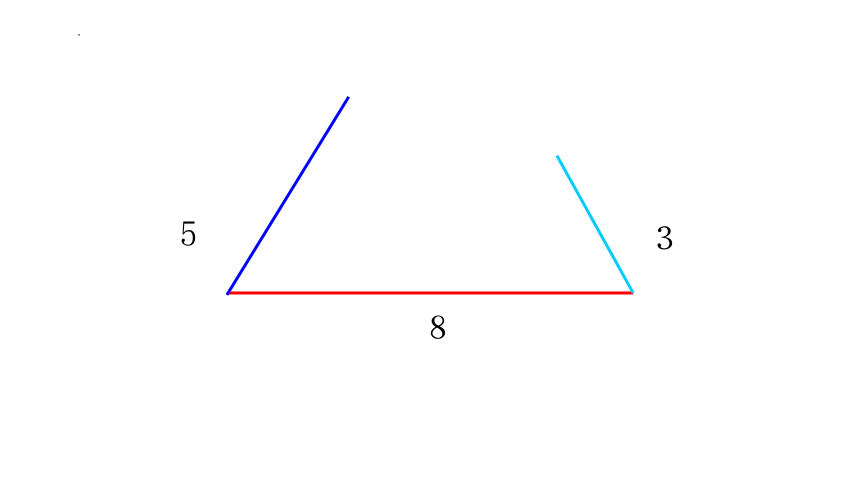
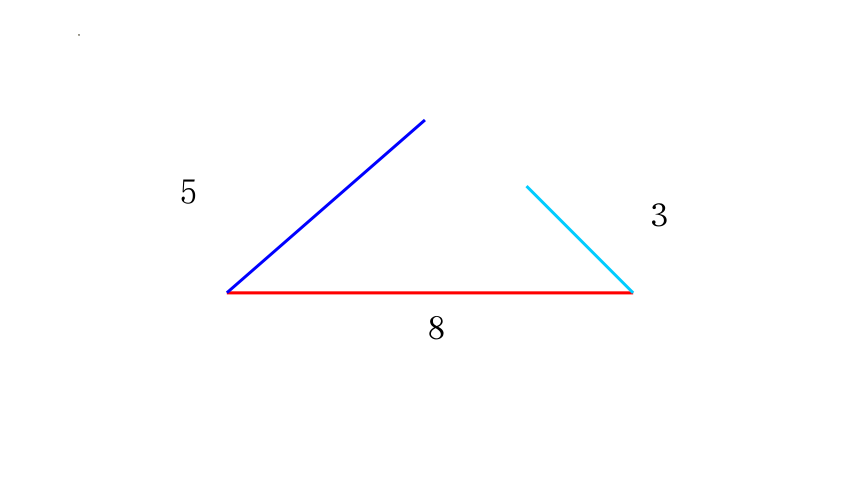
5
8
3
探索
与
发现
5
8
3
5
8
3
5
8
3
5
8
3
不能围成三角形
操作要求:
1、以小组为单位任意选择三根小棒(4cm、5cm、6cm、8cm、10cm,共5根) ,摆一摆,看能否围成三角形。
2、填写表格,做好记录。
探索
组别 所选小棒的长度(厘米) 任意两根小棒长度之和与第三根小木棒的长度关系 特点 能否围成三角形
1 ( 4) (5) (10)
2 ( 4) ( 6) (10)
3 ( 5) (6) (8)
4 (6) (8) (10)
…… …… ……
探索
组别 所选小棒的长度(厘米) 任意两根小棒长度之和与第三根小木棒的长度关系 特点 能否围成三角形
1 ( 4) (5) (10) 4+5<10 4+10>5 5+10>4 较短两条线段之和小于第三条线段 否
2 ( 4) ( 6) (10) 4+6=10 4+10>6 6+10>4 较短两条线段之和等于第三条线段 否
3 ( 5) (6) (8) 5+6>8 5+8>6 6+8>5 任意两条线段之和大于第三条线段 是
4 (6) (8) (10) 6+8>10 6+10>8 8+10>6 任意两条线段之和大于第三条线段 是
… …… ……
思考:三条线段满足怎么样条件才能围成一个三角形?
发现
1、任意两条线段之和大于第三条线段时,则能围成三角形。
2、较短两条线段长度之和小于(或等于)第三条线段时,则不能围成三角形。
判断方法:只要较短两条线段之大于第三条线段,就能围成三角形。
5+3 6
5+6 3
3+6 5
4+3 6
3+6 4
6+4 3
任意一个三角形的任意两边的和都大于第三边
探索与发现:在围成的三角形中,我们发现任意两边之和大于第三边,是不是在任意的三角形中都有这样的特点呢?
活动要求:先请同学们在本子上任意画一个三角形,再量一量、算一算、比一比来验证.
>
>
>
>
>
>
为什么小明走第二条路最近?
①
②
1.公正小法官
①三条线段一定能围成一个三角形。 ( )
②三角形的三边可以相等。 ( )
③三角形任意两边之和大于第三边。 ( )
④三角形最长的一边可能等于其他两边之和。 ( )
×
√
√
×
2.我来选一选
下面三条线段能围成三角形的是( )
A 3厘米、2厘米、5厘米 B 5厘米、5厘米、11厘米
C 5厘米、4米、8厘米 D 4.2厘米、5.8厘米、8厘米
D
3.你来摆一摆
从下面5根小棒中任意选出3根,能摆多少种不同的三角形?
大
道
图 书 馆
教
学
楼
草坪
请勿
践踏!
尽管草地不允许踩,但还是被人们踩出了一条小路,这是为什么?我们能不能运用今天所学的知识解释这一现象?
4.我来说一说
探究思考:有两根树干,一根长8米,另一根长3米,要做一个三角形屋架。请你想一想,第三根树干可能有多长?
教学阐释
流 程
教材分析
(学情分析)
教学学法
教学目标
教学过程
教学阐释
《三角形边的关系》
三角形边的关系教学阐释
一、教材分析
教材编写特点
本课属于“空间与图形”范畴的知识系列。三角形是最基本、最重要的多边形。教材积极创设了动手操作的情境,力求让学生在活动中感知、体会并进行探究出三角形三边关系。
后续学习的相关内容
三角形和四边形的联系
本节课的内容:
三角形三边的关系,加深对三角形的认识。
1、教材地位与作用
2、学情分析:从知识起点上看,对于三角形,学生并不陌生,通过前面的学习,学生已经初步认识了三角形,知道三角形有三条边、三个顶点和三个角,以及三角形稳定性的知识,这些都是学生进一步进行学习的基础。从能力上看,学生乐于动手,喜欢实践,并在前几年的学习中,掌握了一定的实践方法和思考方式,同时比较善于发现和总结,这也将为本节课的学习做好铺垫。从情感上看,学生正处于好奇心强,希望探索未知世界阶段,教师应充分引用生活实例,帮助学生构建三角形边的概念。
二、教学目标
知识技能
过程与方法
情感态度
三角形边的关系
探索并发现三角形两边之和大于第三边,能运用三角形三边关系解决简单的实际问题。。
激发学生对数学的探究兴趣,提高学生自主探索和合作交流的能力。
教学难点
理解三角形任意两边之和大于第三边的真正含义。
教学重点
探究三角形边的关系:三角形任意两边之和大于第三边。
通过动手操作、分析数据,体验探索和发现三角形边的关系的过程,培养发现问题的意识和解决问题的能力,积累探索问题方法和经验。进一步发展空间观念。
教法:动画演示法、引导发现法,活动探究法。通过动画演示引导学生观察、分析,初步感知围成三角形的条件,再通过活动探究引导观察、分析、对比、总结出三角形三边关系。
义务教育《数学课程标准》指出:“学生学习应当是一个生动活泼主动的和富有个性的过程,认真听讲、积极思考、动手实践、自主探索、合作交流等都是学习数学的重要方式,学生应该有足够的时间和空间经历观察实验猜测推理验证等活动过程。”
认知水平
三、教法、学法
学法:动手实践、自主探究、合作交流,引导学生尝试自主提出猜想,在动手操作摆一摆、算一算、归纳总结等方法来验证猜想,探究三角形三边的关系。
(一)创设情境 ,引入新课
四、教学流程
1、说一说,从小明家到学校有几条路可走?
2、你认为走哪条路最近?为什么呢?
设计思想:从学生的生活经验和已有的知识背景出发,引导学生仔细观察,独立思考,为什么这条路最近?让学生先解释生活现象,引发学生对概念的思考,激发学生学习兴趣。
(二)动手操作,探索新知
设计意图:首先老师提出问题:任意三条线段都能围成三角形吗?引发学生思考,紧接着,通过演示两组线段不能围成三角形,引起学生认知冲突,借助演示过程,引导 学生分析不能围成三角形的原因,让学生初步体会到两条线段之和等于(小于)第三条线段时不能围成成三角形,为后面进一步探究满足怎样三条线段才能围成三角形作了很好的铺垫。
活动一:初步感知 ,分析猜想
(二)动手操作,探索新知
活动二:验证猜想 ,深化探究
设计思想:通过小组合作,动手实践,让学生摆一摆三角形,算一算任意两根小棒长度之和与第三根小棒之间的关系,在师生交流、生生交流中探索三根小棒围成三角形的必要条件——较短两条线段之和大于第三条线段。在此基础之上,让学生自主探究任意三角形三边的关系就水到渠成了。让学生亲身经历完整的、科学的研究问题的过程,即提出猜想—实验验证—得出结论的全过程。
(三)巩固练习,拓展应用
设计意图:在练习中,习题设计贴近生活,从概念性知识到应用性知识,从知识本位到知识的应用,由浅入深,螺旋式上升。巩固所学新知,使学生的思维得到升华。
(四)归纳总结,完善认知
这节课你们有什么收获?还有什么问题?你认为你这节课表现怎么样?
设计意图:作业设计遵循学生认知发展规律,突出重难点,既巩固新知,又发展了学生数学思维。
(五)作业布置,巩固延伸
设计意图:让学生发表自己的意见,给他们一个知识梳理和设疑问难的机会,同时对自己和同伴学习进行评价,树立学生自信心。
我的反思
1、说一说,从小明家到学校有几条路可走?
2、你认为走哪条路最近?为什么呢?
问题1:什么是三角形?
问题2: 是不是任意给出三条线段都能围成一个三角形呢?
8
3
8
3
5
4
8
3
探索
与
发现
4
8
3
4
8
3
4
8
3
4
8
3
不能围成三角形
5
8
3
探索
与
发现
5
8
3
5
8
3
5
8
3
5
8
3
不能围成三角形
操作要求:
1、以小组为单位任意选择三根小棒(4cm、5cm、6cm、8cm、10cm,共5根) ,摆一摆,看能否围成三角形。
2、填写表格,做好记录。
探索
组别 所选小棒的长度(厘米) 任意两根小棒长度之和与第三根小木棒的长度关系 特点 能否围成三角形
1 ( 4) (5) (10)
2 ( 4) ( 6) (10)
3 ( 5) (6) (8)
4 (6) (8) (10)
…… …… ……
探索
组别 所选小棒的长度(厘米) 任意两根小棒长度之和与第三根小木棒的长度关系 特点 能否围成三角形
1 ( 4) (5) (10) 4+5<10 4+10>5 5+10>4 较短两条线段之和小于第三条线段 否
2 ( 4) ( 6) (10) 4+6=10 4+10>6 6+10>4 较短两条线段之和等于第三条线段 否
3 ( 5) (6) (8) 5+6>8 5+8>6 6+8>5 任意两条线段之和大于第三条线段 是
4 (6) (8) (10) 6+8>10 6+10>8 8+10>6 任意两条线段之和大于第三条线段 是
… …… ……
思考:三条线段满足怎么样条件才能围成一个三角形?
发现
1、任意两条线段之和大于第三条线段时,则能围成三角形。
2、较短两条线段长度之和小于(或等于)第三条线段时,则不能围成三角形。
判断方法:只要较短两条线段之大于第三条线段,就能围成三角形。
5+3 6
5+6 3
3+6 5
4+3 6
3+6 4
6+4 3
任意一个三角形的任意两边的和都大于第三边
探索与发现:在围成的三角形中,我们发现任意两边之和大于第三边,是不是在任意的三角形中都有这样的特点呢?
活动要求:先请同学们在本子上任意画一个三角形,再量一量、算一算、比一比来验证.
>
>
>
>
>
>
为什么小明走第二条路最近?
①
②
1.公正小法官
①三条线段一定能围成一个三角形。 ( )
②三角形的三边可以相等。 ( )
③三角形任意两边之和大于第三边。 ( )
④三角形最长的一边可能等于其他两边之和。 ( )
×
√
√
×
2.我来选一选
下面三条线段能围成三角形的是( )
A 3厘米、2厘米、5厘米 B 5厘米、5厘米、11厘米
C 5厘米、4米、8厘米 D 4.2厘米、5.8厘米、8厘米
D
3.你来摆一摆
从下面5根小棒中任意选出3根,能摆多少种不同的三角形?
大
道
图 书 馆
教
学
楼
草坪
请勿
践踏!
尽管草地不允许踩,但还是被人们踩出了一条小路,这是为什么?我们能不能运用今天所学的知识解释这一现象?
4.我来说一说
探究思考:有两根树干,一根长8米,另一根长3米,要做一个三角形屋架。请你想一想,第三根树干可能有多长?
教学阐释
流 程
教材分析
(学情分析)
教学学法
教学目标
教学过程
教学阐释
《三角形边的关系》
三角形边的关系教学阐释
一、教材分析
教材编写特点
本课属于“空间与图形”范畴的知识系列。三角形是最基本、最重要的多边形。教材积极创设了动手操作的情境,力求让学生在活动中感知、体会并进行探究出三角形三边关系。
后续学习的相关内容
三角形和四边形的联系
本节课的内容:
三角形三边的关系,加深对三角形的认识。
1、教材地位与作用
2、学情分析:从知识起点上看,对于三角形,学生并不陌生,通过前面的学习,学生已经初步认识了三角形,知道三角形有三条边、三个顶点和三个角,以及三角形稳定性的知识,这些都是学生进一步进行学习的基础。从能力上看,学生乐于动手,喜欢实践,并在前几年的学习中,掌握了一定的实践方法和思考方式,同时比较善于发现和总结,这也将为本节课的学习做好铺垫。从情感上看,学生正处于好奇心强,希望探索未知世界阶段,教师应充分引用生活实例,帮助学生构建三角形边的概念。
二、教学目标
知识技能
过程与方法
情感态度
三角形边的关系
探索并发现三角形两边之和大于第三边,能运用三角形三边关系解决简单的实际问题。。
激发学生对数学的探究兴趣,提高学生自主探索和合作交流的能力。
教学难点
理解三角形任意两边之和大于第三边的真正含义。
教学重点
探究三角形边的关系:三角形任意两边之和大于第三边。
通过动手操作、分析数据,体验探索和发现三角形边的关系的过程,培养发现问题的意识和解决问题的能力,积累探索问题方法和经验。进一步发展空间观念。
教法:动画演示法、引导发现法,活动探究法。通过动画演示引导学生观察、分析,初步感知围成三角形的条件,再通过活动探究引导观察、分析、对比、总结出三角形三边关系。
义务教育《数学课程标准》指出:“学生学习应当是一个生动活泼主动的和富有个性的过程,认真听讲、积极思考、动手实践、自主探索、合作交流等都是学习数学的重要方式,学生应该有足够的时间和空间经历观察实验猜测推理验证等活动过程。”
认知水平
三、教法、学法
学法:动手实践、自主探究、合作交流,引导学生尝试自主提出猜想,在动手操作摆一摆、算一算、归纳总结等方法来验证猜想,探究三角形三边的关系。
(一)创设情境 ,引入新课
四、教学流程
1、说一说,从小明家到学校有几条路可走?
2、你认为走哪条路最近?为什么呢?
设计思想:从学生的生活经验和已有的知识背景出发,引导学生仔细观察,独立思考,为什么这条路最近?让学生先解释生活现象,引发学生对概念的思考,激发学生学习兴趣。
(二)动手操作,探索新知
设计意图:首先老师提出问题:任意三条线段都能围成三角形吗?引发学生思考,紧接着,通过演示两组线段不能围成三角形,引起学生认知冲突,借助演示过程,引导 学生分析不能围成三角形的原因,让学生初步体会到两条线段之和等于(小于)第三条线段时不能围成成三角形,为后面进一步探究满足怎样三条线段才能围成三角形作了很好的铺垫。
活动一:初步感知 ,分析猜想
(二)动手操作,探索新知
活动二:验证猜想 ,深化探究
设计思想:通过小组合作,动手实践,让学生摆一摆三角形,算一算任意两根小棒长度之和与第三根小棒之间的关系,在师生交流、生生交流中探索三根小棒围成三角形的必要条件——较短两条线段之和大于第三条线段。在此基础之上,让学生自主探究任意三角形三边的关系就水到渠成了。让学生亲身经历完整的、科学的研究问题的过程,即提出猜想—实验验证—得出结论的全过程。
(三)巩固练习,拓展应用
设计意图:在练习中,习题设计贴近生活,从概念性知识到应用性知识,从知识本位到知识的应用,由浅入深,螺旋式上升。巩固所学新知,使学生的思维得到升华。
(四)归纳总结,完善认知
这节课你们有什么收获?还有什么问题?你认为你这节课表现怎么样?
设计意图:作业设计遵循学生认知发展规律,突出重难点,既巩固新知,又发展了学生数学思维。
(五)作业布置,巩固延伸
设计意图:让学生发表自己的意见,给他们一个知识梳理和设疑问难的机会,同时对自己和同伴学习进行评价,树立学生自信心。
我的反思
