人教版六年级下学期数学第六单元几何图形初步复习课件(30张ppt)
文档属性
| 名称 | 人教版六年级下学期数学第六单元几何图形初步复习课件(30张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 397.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-16 10:57:38 | ||
图片预览








文档简介
(共30张PPT)
人教版 六年级 下册
第九章 几何图形初步复习
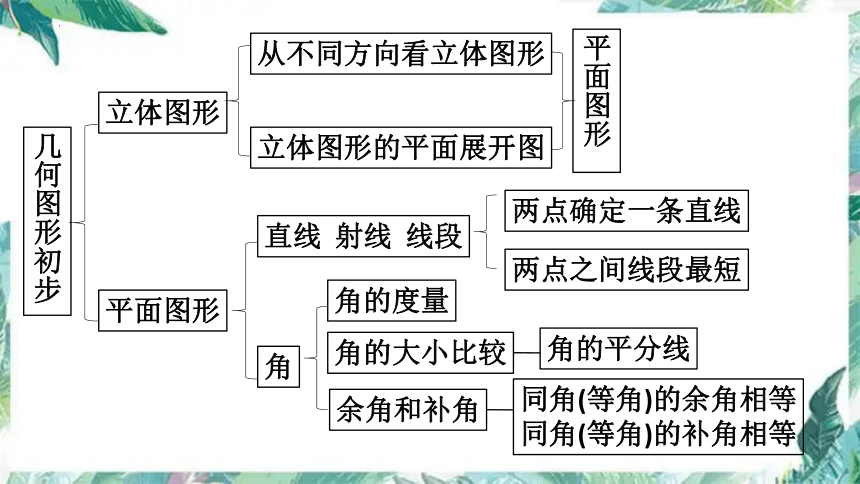
几何图形初步
立体图形
平面图形
从不同方向看立体图形
立体图形的平面展开图
平面图形
直线 射线 线段
角
角的度量
角的大小比较
余角和补角
角的平分线
同角(等角)的余角相等
同角(等角)的补角相等
两点确定一条直线
两点之间线段最短
立体图形的三视图
同一个立体图形从不同的方向看它会得到不同的平面图形。一般包括:
从正面看
(主视图)
从左面看
(左视图)
从上面看
(俯视图)
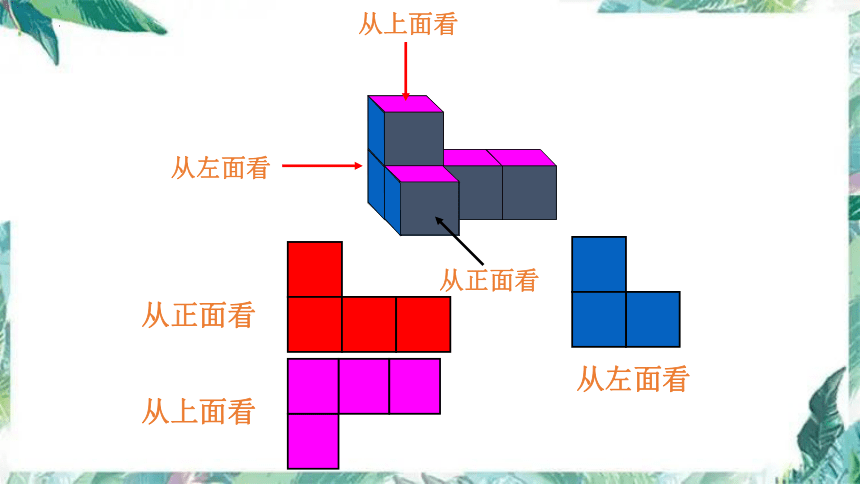
画常见立体图形的三视图
从上面看
从左面看
从正面看
从正面看
从左面看
从上面看
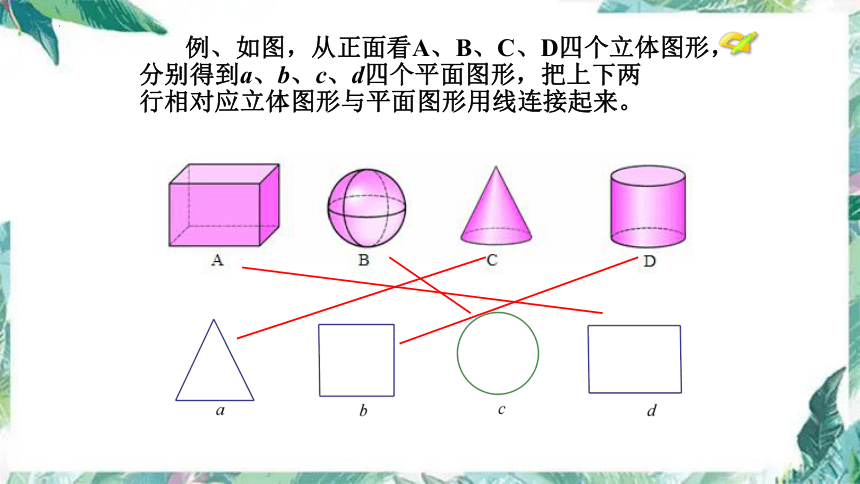
例、如图,从正面看A、B、C、D四个立体图形,分别得到a、b、c、d四个平面图形,把上下两
行相对应立体图形与平面图形用线连接起来。
A
B
B
立体图形的展开图
一些简单的立体图形的展开图、侧面展开图(看课件)
点、线、面、体
点动成线,线动成面,面动成体(几何体)。
立体图形的平面展开图
例 如图所示的图形中,不是正方体表面展开图的是( )
C
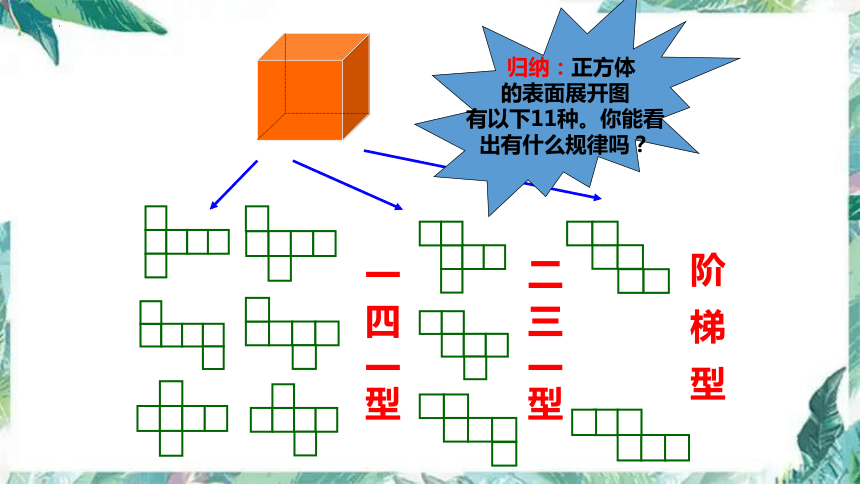
归纳:正方体
的表面展开图
有以下11种。你能看
出有什么规律吗?
一 四 一型
二 三 一型
阶 梯 型
图例 表示方法 特征 性质
直线 A B . . 没有端点,无始无终无方向,看不见首尾,无长度。
射线 O F . n 一个端点,有始无终有方向,看得见首望不到尾,无长度。
线段 C D . . a 两个端点,有始有终无方向,看得见首尾,有长度。
(1)直线AB或直线
BA (字母无序)
(2)直线m
(1)射线OF(字母
有序)
(2)射线n
(1)线段CD或线段
DC(字母无序)
(2)线段a
两点确定一条直线。
两点之间,
线段最短。
用一个钉子把一根细木条钉在木板上,用手拨木条,木条能转动,这表明 ;用两个钉子把细木条钉在木板上,就能固定细木条,这说明 。
过一点有无数条直线
两点确定一条直线
例:AB是一段火车路线图,图中字母表示的五个点表示五个车站,在这段路线上往返行车,需印制几种车票?(每种车票都要印出上车站与下车站)
A C D E B
已知:A、B、C、D四点,请在图中找出一点P,使PA+PB+PC+PD最小。
P
例:平原上有A、B、C、D四个村庄,如图所示,为解决当地缺水问题,政府准备投资修建一个蓄水池,不考虑其他因素,请你画图确定蓄水池H的位置,使它与四个村庄的距离之和最小.
·
·
·
·
A
B
C
D
线段的和、差
a.线段的和
A B C
. . .
AC=AB+BC
b.线段的差
M N P
. . .
MN=MP-NP
NP=MP-MN
(2)线段的中点
把一条线段分成两条相等线段的点,叫做这条线段的中点(middle point)。
线段的大小和比较
(1)线段的比较
度量法
叠合法
AB=BC=
AC
AC=2AB=2BC
例如:点B是线段AC的中点
. . .
A
B
C
则有:
(3)线段的三等分点
把一条线段分成三条相等线段的两个点,叫做这条线段的三等分点。
. . . .
A B C D
AB=BC=CD=
AD
AD=3AB=3BC=3CD
(4)画一条线段等于已知线段
注意耶
用尺规作图法
(5)两点的距离与线段的区别
两点的距离是指连接两点间的线段的长度,是一个数量;
而线段本身是图形.
如图,已知线段AB,延长线段AB到C,使BC=AB.
A
B
C
点B为线段AC的中点,
那么AC= AB= BC;
AB= = AC
想一想
1
2
2
2
BC
判断:
若AM=BM,则M为线段AB的中点。
线段中点的条件:
1、点在已知线段上。
2、点把已知线段分成两条相等线段的点
A
B
M
×
1.如图 AB=6cm,点C是AB的中点,点D是CB的中点,则AD=____cm
4.5
如图,AB = 6厘米,点C是线段AB的中点,点D是线段AB的中点,求线段AD的长.
.
.
.
.
A
C
D
B
6厘米
?厘米
∵ 点C是线段AB的中点,AB=6cm
∴ AC = BC = AB
= 3厘米
∵ 点D是线段BC的中点,
∴ CD = BC
= 1.5厘米
∴ AD = AC + CD
= 3 + 1.5
= 4.5厘米
2.如图,下列说法 ,不能判断点C是线段AB的中点的是( )
A、AC=CB B、AB=2AC
C、AC+CB=AB D、CB= AB
C
例 点A、B、C 在同一条直线上,
AB=3 cm,BC=1 cm.求AC的长.
解:(1)如图①,
∵AB=3 ,BC=1,
∴AC=AB+BC=3+1=4(cm).
(2)如图②,
∵AB=3,BC=1,
∴AC=AB-BC=3-1=2(cm).
1、如图,AB=CD,则AC与BD的大小关系是( )
A、AC>BD B、ACA
B
C
D
2、已知AB=6cm,AD=4cm,BC=5cm,则CD= 。
A
C
D
B
C
3cm
3.已知线段AB=5,AC=3,你能求出线段BC的长度吗?
已知线段AB=12cm,直线AB上有一点C,BC=6cm,M是线段AC的中点,求线段AM的长。
提示:分两种情况
(1)M在线段AC上,
(2)C点在线段AB的延长线上
A
M
C
B
A
M
C
B
根据下列语句画图并计算:
(1)作线段AB,在线段AB的延长线上取点C,使BC=2AB,M是BC的中点,若AB=30cm,求BM的长。
使BC=2AB,M是AC的中点,若AB=30m,
求BM的长。
如图,点C是线段AB上任意一点,点D是线段AC的中点,点E是线段BC的中点,则线段DE和线段AB有怎样的关系?说明理由.
.
.
A
B
.
C
.
.
D
E
解:
∵点D是线段AC的中点
∴ DC = AC
∵点E是线段BC的中点
∴ CE = BC
∴ DE
= DC + CE
= AC + BC
= (AC + BC)
= AB
DE = AB
理由如下:
4、点A、B、C 、 D是直线上顺次四个点,且AB:BC:CD=2:3:4,
如果AC=10cm,求线段BC的长。
知识结构
5. 在直线a上顺次截取A、B、C三点,使得 AB=4cm,BC=3cm.如果点o是线段AC的中点,求线段OB的长。
a
A
C
B
O
0.5cm
人教版 六年级 下册
第九章 几何图形初步复习
几何图形初步
立体图形
平面图形
从不同方向看立体图形
立体图形的平面展开图
平面图形
直线 射线 线段
角
角的度量
角的大小比较
余角和补角
角的平分线
同角(等角)的余角相等
同角(等角)的补角相等
两点确定一条直线
两点之间线段最短
立体图形的三视图
同一个立体图形从不同的方向看它会得到不同的平面图形。一般包括:
从正面看
(主视图)
从左面看
(左视图)
从上面看
(俯视图)
画常见立体图形的三视图
从上面看
从左面看
从正面看
从正面看
从左面看
从上面看
例、如图,从正面看A、B、C、D四个立体图形,分别得到a、b、c、d四个平面图形,把上下两
行相对应立体图形与平面图形用线连接起来。
A
B
B
立体图形的展开图
一些简单的立体图形的展开图、侧面展开图(看课件)
点、线、面、体
点动成线,线动成面,面动成体(几何体)。
立体图形的平面展开图
例 如图所示的图形中,不是正方体表面展开图的是( )
C
归纳:正方体
的表面展开图
有以下11种。你能看
出有什么规律吗?
一 四 一型
二 三 一型
阶 梯 型
图例 表示方法 特征 性质
直线 A B . . 没有端点,无始无终无方向,看不见首尾,无长度。
射线 O F . n 一个端点,有始无终有方向,看得见首望不到尾,无长度。
线段 C D . . a 两个端点,有始有终无方向,看得见首尾,有长度。
(1)直线AB或直线
BA (字母无序)
(2)直线m
(1)射线OF(字母
有序)
(2)射线n
(1)线段CD或线段
DC(字母无序)
(2)线段a
两点确定一条直线。
两点之间,
线段最短。
用一个钉子把一根细木条钉在木板上,用手拨木条,木条能转动,这表明 ;用两个钉子把细木条钉在木板上,就能固定细木条,这说明 。
过一点有无数条直线
两点确定一条直线
例:AB是一段火车路线图,图中字母表示的五个点表示五个车站,在这段路线上往返行车,需印制几种车票?(每种车票都要印出上车站与下车站)
A C D E B
已知:A、B、C、D四点,请在图中找出一点P,使PA+PB+PC+PD最小。
P
例:平原上有A、B、C、D四个村庄,如图所示,为解决当地缺水问题,政府准备投资修建一个蓄水池,不考虑其他因素,请你画图确定蓄水池H的位置,使它与四个村庄的距离之和最小.
·
·
·
·
A
B
C
D
线段的和、差
a.线段的和
A B C
. . .
AC=AB+BC
b.线段的差
M N P
. . .
MN=MP-NP
NP=MP-MN
(2)线段的中点
把一条线段分成两条相等线段的点,叫做这条线段的中点(middle point)。
线段的大小和比较
(1)线段的比较
度量法
叠合法
AB=BC=
AC
AC=2AB=2BC
例如:点B是线段AC的中点
. . .
A
B
C
则有:
(3)线段的三等分点
把一条线段分成三条相等线段的两个点,叫做这条线段的三等分点。
. . . .
A B C D
AB=BC=CD=
AD
AD=3AB=3BC=3CD
(4)画一条线段等于已知线段
注意耶
用尺规作图法
(5)两点的距离与线段的区别
两点的距离是指连接两点间的线段的长度,是一个数量;
而线段本身是图形.
如图,已知线段AB,延长线段AB到C,使BC=AB.
A
B
C
点B为线段AC的中点,
那么AC= AB= BC;
AB= = AC
想一想
1
2
2
2
BC
判断:
若AM=BM,则M为线段AB的中点。
线段中点的条件:
1、点在已知线段上。
2、点把已知线段分成两条相等线段的点
A
B
M
×
1.如图 AB=6cm,点C是AB的中点,点D是CB的中点,则AD=____cm
4.5
如图,AB = 6厘米,点C是线段AB的中点,点D是线段AB的中点,求线段AD的长.
.
.
.
.
A
C
D
B
6厘米
?厘米
∵ 点C是线段AB的中点,AB=6cm
∴ AC = BC = AB
= 3厘米
∵ 点D是线段BC的中点,
∴ CD = BC
= 1.5厘米
∴ AD = AC + CD
= 3 + 1.5
= 4.5厘米
2.如图,下列说法 ,不能判断点C是线段AB的中点的是( )
A、AC=CB B、AB=2AC
C、AC+CB=AB D、CB= AB
C
例 点A、B、C 在同一条直线上,
AB=3 cm,BC=1 cm.求AC的长.
解:(1)如图①,
∵AB=3 ,BC=1,
∴AC=AB+BC=3+1=4(cm).
(2)如图②,
∵AB=3,BC=1,
∴AC=AB-BC=3-1=2(cm).
1、如图,AB=CD,则AC与BD的大小关系是( )
A、AC>BD B、AC
B
C
D
2、已知AB=6cm,AD=4cm,BC=5cm,则CD= 。
A
C
D
B
C
3cm
3.已知线段AB=5,AC=3,你能求出线段BC的长度吗?
已知线段AB=12cm,直线AB上有一点C,BC=6cm,M是线段AC的中点,求线段AM的长。
提示:分两种情况
(1)M在线段AC上,
(2)C点在线段AB的延长线上
A
M
C
B
A
M
C
B
根据下列语句画图并计算:
(1)作线段AB,在线段AB的延长线上取点C,使BC=2AB,M是BC的中点,若AB=30cm,求BM的长。
使BC=2AB,M是AC的中点,若AB=30m,
求BM的长。
如图,点C是线段AB上任意一点,点D是线段AC的中点,点E是线段BC的中点,则线段DE和线段AB有怎样的关系?说明理由.
.
.
A
B
.
C
.
.
D
E
解:
∵点D是线段AC的中点
∴ DC = AC
∵点E是线段BC的中点
∴ CE = BC
∴ DE
= DC + CE
= AC + BC
= (AC + BC)
= AB
DE = AB
理由如下:
4、点A、B、C 、 D是直线上顺次四个点,且AB:BC:CD=2:3:4,
如果AC=10cm,求线段BC的长。
知识结构
5. 在直线a上顺次截取A、B、C三点,使得 AB=4cm,BC=3cm.如果点o是线段AC的中点,求线段OB的长。
a
A
C
B
O
0.5cm
