沪科版八年级数学下册 第19章《四边形》名校优选检测题(含答案)
文档属性
| 名称 | 沪科版八年级数学下册 第19章《四边形》名校优选检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-16 12:25:24 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
沪科版八年级数学下册 第19章 名校优选检测题
(时间:120分钟,满分:150分)
班级: 姓名: 成绩: .
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A,B,C,D四个选项,其中只有一个是符合题目要求的.
1.在 ABCD中,AD=4 cm,AB=2 cm,则 ABCD的周长等于( )
A.12 cm B.8 cm C.6 cm D.4 cm
2.如果正多边形的一个内角等于135°,那么这个正多边形的边数是( )
A.5 B.6 C.7 D.8
3.已知四边形ABCD中,对角线AC,BD交于点O,则下列选项中不能证明四边形ABCD为平行四边形的是( )
A.AB∥CD,AB=CD B.AB=CD,BC=AD
C.AB∥CD,AC=BD D.OA=OC,OB=OD
4.四边形ABCD中,AC⊥BD,AC≠BD,顺次连接各边中点得到的四边形是( )
A.正方形 B.矩形 C.菱形 D.以上都不是
5.只用下列图形不能进行平面镶嵌的是( )
A.全等的三角形 B.全等的四边形
C.全等的正五边形 D.全等的正六边形
6.如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( )
A. B. C.4 D.
7.如图,在边长为4的等边三角形ABC中,点D,E分别是边BC,AC的中点,DF⊥AB于点F,连接EF,则EF的长为( )
A. B.2.5 C. D.3
8.如图,在 ABCD中,E为BC边上一点,以AE为边作正方形AEFG,若∠BAE=40°,∠CEF=15°,则∠D的度数是( )
A.65° B.55° C.70° D.75°
9.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF,若AB=3,则BC的长为( )
A.1 B. C.2 D.
10.如图,l1∥l2∥l3,且相邻两条直线间的距离都是2,A,B,C分别为l1,l2,l3上的动点,连接AB,AC,BC,AC与l2交于点D,∠ABC=90°,则BD的最小值为( )
A.2 B.3 C.4 D.5
二、填空题(本大题共4小题,每小题5分,满分20分)
11.在△ABC中,∠ACB=90°,∠A=α,CD是中线,则∠DCB= .(用含α的代数式表示)
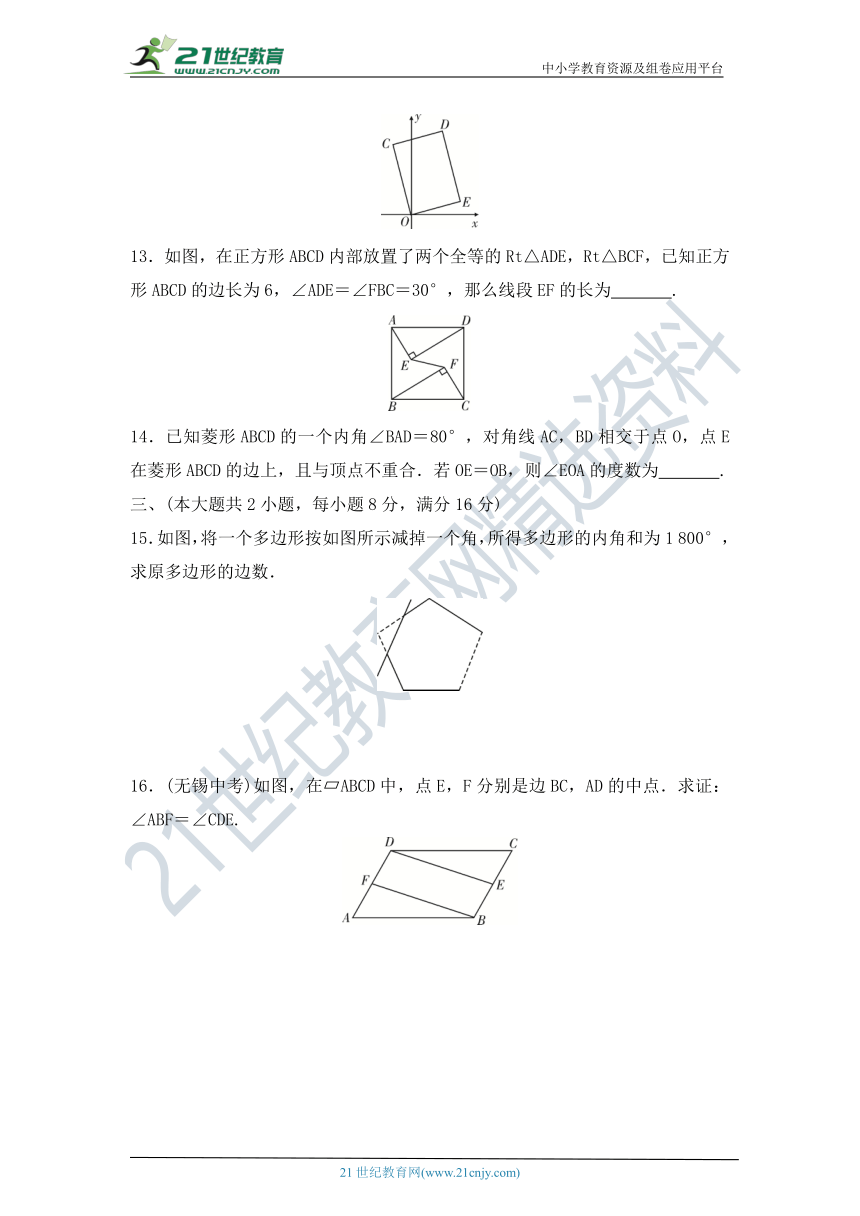
12.如图,在矩形COED中,点D的坐标是(3,7),则CE的长是 .
13.如图,在正方形ABCD内部放置了两个全等的Rt△ADE,Rt△BCF,已知正方形ABCD的边长为6,∠ADE=∠FBC=30°,那么线段EF的长为 .
14.已知菱形ABCD的一个内角∠BAD=80°,对角线AC,BD相交于点O,点E在菱形ABCD的边上,且与顶点不重合.若OE=OB,则∠EOA的度数为 .
三、(本大题共2小题,每小题8分,满分16分)
15.如图,将一个多边形按如图所示减掉一个角,所得多边形的内角和为1 800°,求原多边形的边数.
16.(无锡中考)如图,在 ABCD中,点E,F分别是边BC,AD的中点.求证:∠ABF=∠CDE.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,AD是△ABC的角平分线,DE∥AB,在AB上截取BF=AE,求证:EF=BD.
18.用无刻度的直尺按要求作图(请保留作图痕迹,不写作法).
(1)如图①,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是矩形,请在图中画出∠AOB的平分线;
(2)如图②,在8×6的正方形网格中,请画出一个与△ABC面积相等,且以BC为边,各顶点均在格点上的平行四边形.
五、(本大题共2小题,每小题10分,满分20分)
19.(盐城中考)如图,在正方形ABCD中,对角线BD所在的直线上有E,F两点,且满足BE=DF,连接AE,AF,CE,CF.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.
20.如图,四边形ABCD中,对角线AC,BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形;
(2)若∠AOB∶∠ODC=8∶5,求∠ADO的度数.
六、(本题满分12分)
21.【问题情境】在学习四边形的时候,我们曾学习过一些特殊四边形的性质,如菱形的对角线互相垂直.其实日常生活中,还有很多四边形.如图,堤坝横截面(图①)、水渠横截面(图②)都是一组对边平行而另一组对边不平行的四边形,我们把这种四边形叫做“梯形”,当不平行的一组对边相等时,这种梯形又叫做等腰梯形.
【分析研究】如图③,在四边形ABCD中,AB∥CD,AD=BC.请用学过的知识,探究等腰梯形ABCD的相关性质,写出其中一条即可,并说明理由.
【我的探究】性质: .
③
七、(本题满分12分)
22.我们给出如下定义:有一组相邻内角相等的四边形叫做等邻角四边形.请解答下列问题.
(1)写出一个你所学过的特殊四边形中是等邻角四边形的图形的名称;
(2)如图①,在△ABC中,AB=AC,点D在BC上,且CD=AC,E,F分别为BC,AD的中点,连接EF并延长交AB于点G.求证:四边形AGEC是等邻角四边形;
(3)如图②,若点D在△ABC的内部,(2)中的其他条件不变,EF交CD于点H,图中是否存在等邻角四边形?若存在,指出是哪个四边形,不必证明;若不存在,请说明理由.
八、(本题满分14分)
23.如图,已知△ABC和△DEF是两个边长都为1 cm的等边三角形,且点B,D,C,E都在同一直线上,连接AD,CF.
(1)求证:四边形ADFC是平行四边形;
(2)若BD=0.3 cm,△ABC沿着BE的方向以每秒1 cm的速度运动,设△ABC运动的时间为t秒.
①当t为何值时,四边形ADFC是菱形?请说明理由;
②四边形ADFC有可能是矩形吗?若可能,求出t的值及此矩形的面积;若不可能,请说明理由.
题图
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A,B,C,D四个选项,其中只有一个是符合题目要求的.
1.在 ABCD中,AD=4 cm,AB=2 cm,则 ABCD的周长等于(A)
A.12 cm B.8 cm C.6 cm D.4 cm
2.如果正多边形的一个内角等于135°,那么这个正多边形的边数是(D)
A.5 B.6 C.7 D.8
3.已知四边形ABCD中,对角线AC,BD交于点O,则下列选项中不能证明四边形ABCD为平行四边形的是(C)
A.AB∥CD,AB=CD B.AB=CD,BC=AD
C.AB∥CD,AC=BD D.OA=OC,OB=OD
4.四边形ABCD中,AC⊥BD,AC≠BD,顺次连接各边中点得到的四边形是(B)
A.正方形 B.矩形 C.菱形 D.以上都不是
5.只用下列图形不能进行平面镶嵌的是(C)
A.全等的三角形 B.全等的四边形
C.全等的正五边形 D.全等的正六边形
6.如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为(D)
A. B. C.4 D.
7.如图,在边长为4的等边三角形ABC中,点D,E分别是边BC,AC的中点,DF⊥AB于点F,连接EF,则EF的长为(C)
A. B.2.5 C. D.3
8.如图,在 ABCD中,E为BC边上一点,以AE为边作正方形AEFG,若∠BAE=40°,∠CEF=15°,则∠D的度数是(A)
A.65° B.55° C.70° D.75°
9.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF,若AB=3,则BC的长为(D)
A.1 B. C.2 D.
10.如图,l1∥l2∥l3,且相邻两条直线间的距离都是2,A,B,C分别为l1,l2,l3上的动点,连接AB,AC,BC,AC与l2交于点D,∠ABC=90°,则BD的最小值为(A)
A.2 B.3 C.4 D.5
二、填空题(本大题共4小题,每小题5分,满分20分)
11.在△ABC中,∠ACB=90°,∠A=α,CD是中线,则∠DCB=
90°-α.(用含α的代数式表示)
12.如图,在矩形COED中,点D的坐标是(3,7),则CE的长是.
13.如图,在正方形ABCD内部放置了两个全等的Rt△ADE,Rt△BCF,已知正方形ABCD的边长为6,∠ADE=∠FBC=30°,那么线段EF的长为3-3.
14.已知菱形ABCD的一个内角∠BAD=80°,对角线AC,BD相交于点O,点E在菱形ABCD的边上,且与顶点不重合.若OE=OB,则∠EOA的度数为10°或170°.
三、(本大题共2小题,每小题8分,满分16分)
15.如图,将一个多边形按如图所示减掉一个角,所得多边形的内角和为1 800°,求原多边形的边数.
解:设多边形截去一个角后的边数为n.根据题意,得(n-2)·180°= 1 800°,
解得n=12.
∵截去一个角后,边数增加1,
∴原多边形的边数是11.
16.(无锡中考)如图,在 ABCD中,点E,F分别是边BC,AD的中点.求证:∠ABF=∠CDE.
证明:∵四边形ABCD是平行四边形,∴AD=BC,∠A=∠C,
∵E,F分别是边BC,AD的中点,∴AF=CE,
在△ABF和△CDE中,
∴△ABF≌△CDE(SAS),∴∠ABF=∠CDE.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,AD是△ABC的角平分线,DE∥AB,在AB上截取BF=AE,求证:EF=BD.
证明:∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,∵DE∥AB,
∴∠EDA=∠BAD,
∴∠EDA=∠CAD,
∴AE=DE.∵BF=AE,∴BF=DE,
∴四边形BDEF为平行四边形,∴EF=BD.
18.用无刻度的直尺按要求作图(请保留作图痕迹,不写作法).
(1)如图①,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是矩形,请在图中画出∠AOB的平分线;
(2)如图②,在8×6的正方形网格中,请画出一个与△ABC面积相等,且以BC为边,各顶点均在格点上的平行四边形.
解:(1)如图①,射线OP即为所求.
(2)如图②,平行四边形BCMN即为所求(答案不唯一).
五、(本大题共2小题,每小题10分,满分20分)
19.(盐城中考)如图,在正方形ABCD中,对角线BD所在的直线上有E,F两点,且满足BE=DF,连接AE,AF,CE,CF.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.
(1)证明:∵四边形ABCD是正方形,∴AB=AD,
∴∠ABD=∠ADB,∴∠ABE=∠ADF,
在△ABE与△ADF中,∴△ABE≌△ADF.
(2)解:四边形AECF是菱形.理由:连接AC,交BD于点O.
∵四边形ABCD是正方形,∴OA=OC,OB=OD,AC⊥EF,
∴OB+BE=OD+DF,即OE=OF.
∵OA=OC,OE=OF,∴四边形AECF是平行四边形.又∵AC⊥EF,∴四边形AECF是菱形.
20.如图,四边形ABCD中,对角线AC,BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形;
(2)若∠AOB∶∠ODC=8∶5,求∠ADO的度数.
(1)证明:∵AO=OC,BO=OD,∴四边形ABCD是平行四边形,
∵∠AOB=∠DAO+∠ADO=2∠OAD,∴∠DAO=∠ADO,
∴AO=DO,∴AC=BD,∴平行四边形ABCD是矩形.
(2)解:∵四边形ABCD是矩形,∴AB∥CD,∠BAD=90°,
∴∠ABO=∠CDO,∵∠AOB∶∠ODC=8∶5,∴∠AOB∶∠ABO=8∶5,
∴∠BAO∶∠AOB∶∠ABO=5∶8∶5,∴∠ABO=50°,∵∠BAD=90°,
∴∠ADO=90°-50°=40°.
六、(本题满分12分)
21.【问题情境】在学习四边形的时候,我们曾学习过一些特殊四边形的性质,如菱形的对角线互相垂直.其实日常生活中,还有很多四边形.如图,堤坝横截面(图①)、水渠横截面(图②)都是一组对边平行而另一组对边不平行的四边形,我们把这种四边形叫做“梯形”,当不平行的一组对边相等时,这种梯形又叫做等腰梯形.
【分析研究】如图③,在四边形ABCD中,AB∥CD,AD=BC.请用学过的知识,探究等腰梯形ABCD的相关性质,写出其中一条即可,并说明理由.
【我的探究】性质:等腰梯形的同一底上的两个角相等.
③
解:理由:过点C作CE∥DA交AB于点E,
∵AB∥CD,∴四边形AECD是平行四边形,∴AD=EC,AD∥EC,
∵AD=BC,∴EC=BC,∴∠CEB=∠B,
∵AD∥EC,∴∠CEB=∠A,∴∠A=∠B.
∵CD∥AB,∴∠D+∠A=180°,∠BCD+∠B=180°.
∵∠A=∠B,∴∠D=∠BCD.
七、(本题满分12分)
22.我们给出如下定义:有一组相邻内角相等的四边形叫做等邻角四边形.请解答下列问题.
(1)写出一个你所学过的特殊四边形中是等邻角四边形的图形的名称;
(2)如图①,在△ABC中,AB=AC,点D在BC上,且CD=AC,E,F分别为BC,AD的中点,连接EF并延长交AB于点G.求证:四边形AGEC是等邻角四边形;
(3)如图②,若点D在△ABC的内部,(2)中的其他条件不变,EF交CD于点H,图中是否存在等邻角四边形?若存在,指出是哪个四边形,不必证明;若不存在,请说明理由.
题图
(1)解:答案不唯一,如矩形或正方形.
(2)证明:如答图,连接AE,设∠B的度数为x,
∵AB=AC,CD=AC,BE=CE,
∴∠C=∠B=x,∠1==90°-,AE⊥BC.
∵F是AD的中点,∴AF=DF=EF=AD,∴∠2=∠1=90°-,
∴∠AGE=∠B+∠2=x+90°-=90°+,
∠GEC=180°-=90°+,
∴∠AGE=∠GEC,∴四边形AGEC是等邻角四边形.
(3)解:图②中存在等邻角四边形,四边形AGHC是等邻角四边形.
八、(本题满分14分)
23.如图,已知△ABC和△DEF是两个边长都为1 cm的等边三角形,且点B,D,C,E都在同一直线上,连接AD,CF.
(1)求证:四边形ADFC是平行四边形;
(2)若BD=0.3 cm,△ABC沿着BE的方向以每秒1 cm的速度运动,设△ABC运动的时间为t秒.
①当t为何值时,四边形ADFC是菱形?请说明理由;
②四边形ADFC有可能是矩形吗?若可能,求出t的值及此矩形的面积;若不可能,请说明理由.
题图
答图
(1)证明:∵△ABC和△DEF是两个边长都为1 cm的等边三角形,
∴AC=DF=1 cm,∠ACB=∠FDE=60°,∴AC∥DF,
∴四边形ADFC是平行四边形.
(2)解:①当t=0.3时,四边形ADFC是菱形,理由:∵△ABC沿着BE的方向以每秒1 cm的速度运动,
∴当t==0.3时,点B与点D重合,如答图①所示,则AD=AE=BC=DE=DF=EF,
∴四边形ADFC是菱形.
②有可能.若四边形ADFC是矩形,则∠ADF=90°,如答图②,
∴∠ADC=90°-60°=30°.同理∠DAB=30°=∠ADC,∴BA=BD.同理EC=EF,∴点E与点B重合,
∴t=(1+0.3)÷1=1.3.此时,在Rt△ADF中,∠ADF=90°,DF=1 cm,AF=2 cm,
∴AD===(cm),∴矩形ADFC的面积=AD·DF= cm2.
即当t为1.3时,四边形ADFC是矩形,此矩形的面积为 cm2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
沪科版八年级数学下册 第19章 名校优选检测题
(时间:120分钟,满分:150分)
班级: 姓名: 成绩: .
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A,B,C,D四个选项,其中只有一个是符合题目要求的.
1.在 ABCD中,AD=4 cm,AB=2 cm,则 ABCD的周长等于( )
A.12 cm B.8 cm C.6 cm D.4 cm
2.如果正多边形的一个内角等于135°,那么这个正多边形的边数是( )
A.5 B.6 C.7 D.8
3.已知四边形ABCD中,对角线AC,BD交于点O,则下列选项中不能证明四边形ABCD为平行四边形的是( )
A.AB∥CD,AB=CD B.AB=CD,BC=AD
C.AB∥CD,AC=BD D.OA=OC,OB=OD
4.四边形ABCD中,AC⊥BD,AC≠BD,顺次连接各边中点得到的四边形是( )
A.正方形 B.矩形 C.菱形 D.以上都不是
5.只用下列图形不能进行平面镶嵌的是( )
A.全等的三角形 B.全等的四边形
C.全等的正五边形 D.全等的正六边形
6.如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( )
A. B. C.4 D.
7.如图,在边长为4的等边三角形ABC中,点D,E分别是边BC,AC的中点,DF⊥AB于点F,连接EF,则EF的长为( )
A. B.2.5 C. D.3
8.如图,在 ABCD中,E为BC边上一点,以AE为边作正方形AEFG,若∠BAE=40°,∠CEF=15°,则∠D的度数是( )
A.65° B.55° C.70° D.75°
9.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF,若AB=3,则BC的长为( )
A.1 B. C.2 D.
10.如图,l1∥l2∥l3,且相邻两条直线间的距离都是2,A,B,C分别为l1,l2,l3上的动点,连接AB,AC,BC,AC与l2交于点D,∠ABC=90°,则BD的最小值为( )
A.2 B.3 C.4 D.5
二、填空题(本大题共4小题,每小题5分,满分20分)
11.在△ABC中,∠ACB=90°,∠A=α,CD是中线,则∠DCB= .(用含α的代数式表示)
12.如图,在矩形COED中,点D的坐标是(3,7),则CE的长是 .
13.如图,在正方形ABCD内部放置了两个全等的Rt△ADE,Rt△BCF,已知正方形ABCD的边长为6,∠ADE=∠FBC=30°,那么线段EF的长为 .
14.已知菱形ABCD的一个内角∠BAD=80°,对角线AC,BD相交于点O,点E在菱形ABCD的边上,且与顶点不重合.若OE=OB,则∠EOA的度数为 .
三、(本大题共2小题,每小题8分,满分16分)
15.如图,将一个多边形按如图所示减掉一个角,所得多边形的内角和为1 800°,求原多边形的边数.
16.(无锡中考)如图,在 ABCD中,点E,F分别是边BC,AD的中点.求证:∠ABF=∠CDE.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,AD是△ABC的角平分线,DE∥AB,在AB上截取BF=AE,求证:EF=BD.
18.用无刻度的直尺按要求作图(请保留作图痕迹,不写作法).
(1)如图①,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是矩形,请在图中画出∠AOB的平分线;
(2)如图②,在8×6的正方形网格中,请画出一个与△ABC面积相等,且以BC为边,各顶点均在格点上的平行四边形.
五、(本大题共2小题,每小题10分,满分20分)
19.(盐城中考)如图,在正方形ABCD中,对角线BD所在的直线上有E,F两点,且满足BE=DF,连接AE,AF,CE,CF.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.
20.如图,四边形ABCD中,对角线AC,BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形;
(2)若∠AOB∶∠ODC=8∶5,求∠ADO的度数.
六、(本题满分12分)
21.【问题情境】在学习四边形的时候,我们曾学习过一些特殊四边形的性质,如菱形的对角线互相垂直.其实日常生活中,还有很多四边形.如图,堤坝横截面(图①)、水渠横截面(图②)都是一组对边平行而另一组对边不平行的四边形,我们把这种四边形叫做“梯形”,当不平行的一组对边相等时,这种梯形又叫做等腰梯形.
【分析研究】如图③,在四边形ABCD中,AB∥CD,AD=BC.请用学过的知识,探究等腰梯形ABCD的相关性质,写出其中一条即可,并说明理由.
【我的探究】性质: .
③
七、(本题满分12分)
22.我们给出如下定义:有一组相邻内角相等的四边形叫做等邻角四边形.请解答下列问题.
(1)写出一个你所学过的特殊四边形中是等邻角四边形的图形的名称;
(2)如图①,在△ABC中,AB=AC,点D在BC上,且CD=AC,E,F分别为BC,AD的中点,连接EF并延长交AB于点G.求证:四边形AGEC是等邻角四边形;
(3)如图②,若点D在△ABC的内部,(2)中的其他条件不变,EF交CD于点H,图中是否存在等邻角四边形?若存在,指出是哪个四边形,不必证明;若不存在,请说明理由.
八、(本题满分14分)
23.如图,已知△ABC和△DEF是两个边长都为1 cm的等边三角形,且点B,D,C,E都在同一直线上,连接AD,CF.
(1)求证:四边形ADFC是平行四边形;
(2)若BD=0.3 cm,△ABC沿着BE的方向以每秒1 cm的速度运动,设△ABC运动的时间为t秒.
①当t为何值时,四边形ADFC是菱形?请说明理由;
②四边形ADFC有可能是矩形吗?若可能,求出t的值及此矩形的面积;若不可能,请说明理由.
题图
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A,B,C,D四个选项,其中只有一个是符合题目要求的.
1.在 ABCD中,AD=4 cm,AB=2 cm,则 ABCD的周长等于(A)
A.12 cm B.8 cm C.6 cm D.4 cm
2.如果正多边形的一个内角等于135°,那么这个正多边形的边数是(D)
A.5 B.6 C.7 D.8
3.已知四边形ABCD中,对角线AC,BD交于点O,则下列选项中不能证明四边形ABCD为平行四边形的是(C)
A.AB∥CD,AB=CD B.AB=CD,BC=AD
C.AB∥CD,AC=BD D.OA=OC,OB=OD
4.四边形ABCD中,AC⊥BD,AC≠BD,顺次连接各边中点得到的四边形是(B)
A.正方形 B.矩形 C.菱形 D.以上都不是
5.只用下列图形不能进行平面镶嵌的是(C)
A.全等的三角形 B.全等的四边形
C.全等的正五边形 D.全等的正六边形
6.如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为(D)
A. B. C.4 D.
7.如图,在边长为4的等边三角形ABC中,点D,E分别是边BC,AC的中点,DF⊥AB于点F,连接EF,则EF的长为(C)
A. B.2.5 C. D.3
8.如图,在 ABCD中,E为BC边上一点,以AE为边作正方形AEFG,若∠BAE=40°,∠CEF=15°,则∠D的度数是(A)
A.65° B.55° C.70° D.75°
9.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF,若AB=3,则BC的长为(D)
A.1 B. C.2 D.
10.如图,l1∥l2∥l3,且相邻两条直线间的距离都是2,A,B,C分别为l1,l2,l3上的动点,连接AB,AC,BC,AC与l2交于点D,∠ABC=90°,则BD的最小值为(A)
A.2 B.3 C.4 D.5
二、填空题(本大题共4小题,每小题5分,满分20分)
11.在△ABC中,∠ACB=90°,∠A=α,CD是中线,则∠DCB=
90°-α.(用含α的代数式表示)
12.如图,在矩形COED中,点D的坐标是(3,7),则CE的长是.
13.如图,在正方形ABCD内部放置了两个全等的Rt△ADE,Rt△BCF,已知正方形ABCD的边长为6,∠ADE=∠FBC=30°,那么线段EF的长为3-3.
14.已知菱形ABCD的一个内角∠BAD=80°,对角线AC,BD相交于点O,点E在菱形ABCD的边上,且与顶点不重合.若OE=OB,则∠EOA的度数为10°或170°.
三、(本大题共2小题,每小题8分,满分16分)
15.如图,将一个多边形按如图所示减掉一个角,所得多边形的内角和为1 800°,求原多边形的边数.
解:设多边形截去一个角后的边数为n.根据题意,得(n-2)·180°= 1 800°,
解得n=12.
∵截去一个角后,边数增加1,
∴原多边形的边数是11.
16.(无锡中考)如图,在 ABCD中,点E,F分别是边BC,AD的中点.求证:∠ABF=∠CDE.
证明:∵四边形ABCD是平行四边形,∴AD=BC,∠A=∠C,
∵E,F分别是边BC,AD的中点,∴AF=CE,
在△ABF和△CDE中,
∴△ABF≌△CDE(SAS),∴∠ABF=∠CDE.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,AD是△ABC的角平分线,DE∥AB,在AB上截取BF=AE,求证:EF=BD.
证明:∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,∵DE∥AB,
∴∠EDA=∠BAD,
∴∠EDA=∠CAD,
∴AE=DE.∵BF=AE,∴BF=DE,
∴四边形BDEF为平行四边形,∴EF=BD.
18.用无刻度的直尺按要求作图(请保留作图痕迹,不写作法).
(1)如图①,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是矩形,请在图中画出∠AOB的平分线;
(2)如图②,在8×6的正方形网格中,请画出一个与△ABC面积相等,且以BC为边,各顶点均在格点上的平行四边形.
解:(1)如图①,射线OP即为所求.
(2)如图②,平行四边形BCMN即为所求(答案不唯一).
五、(本大题共2小题,每小题10分,满分20分)
19.(盐城中考)如图,在正方形ABCD中,对角线BD所在的直线上有E,F两点,且满足BE=DF,连接AE,AF,CE,CF.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.
(1)证明:∵四边形ABCD是正方形,∴AB=AD,
∴∠ABD=∠ADB,∴∠ABE=∠ADF,
在△ABE与△ADF中,∴△ABE≌△ADF.
(2)解:四边形AECF是菱形.理由:连接AC,交BD于点O.
∵四边形ABCD是正方形,∴OA=OC,OB=OD,AC⊥EF,
∴OB+BE=OD+DF,即OE=OF.
∵OA=OC,OE=OF,∴四边形AECF是平行四边形.又∵AC⊥EF,∴四边形AECF是菱形.
20.如图,四边形ABCD中,对角线AC,BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形;
(2)若∠AOB∶∠ODC=8∶5,求∠ADO的度数.
(1)证明:∵AO=OC,BO=OD,∴四边形ABCD是平行四边形,
∵∠AOB=∠DAO+∠ADO=2∠OAD,∴∠DAO=∠ADO,
∴AO=DO,∴AC=BD,∴平行四边形ABCD是矩形.
(2)解:∵四边形ABCD是矩形,∴AB∥CD,∠BAD=90°,
∴∠ABO=∠CDO,∵∠AOB∶∠ODC=8∶5,∴∠AOB∶∠ABO=8∶5,
∴∠BAO∶∠AOB∶∠ABO=5∶8∶5,∴∠ABO=50°,∵∠BAD=90°,
∴∠ADO=90°-50°=40°.
六、(本题满分12分)
21.【问题情境】在学习四边形的时候,我们曾学习过一些特殊四边形的性质,如菱形的对角线互相垂直.其实日常生活中,还有很多四边形.如图,堤坝横截面(图①)、水渠横截面(图②)都是一组对边平行而另一组对边不平行的四边形,我们把这种四边形叫做“梯形”,当不平行的一组对边相等时,这种梯形又叫做等腰梯形.
【分析研究】如图③,在四边形ABCD中,AB∥CD,AD=BC.请用学过的知识,探究等腰梯形ABCD的相关性质,写出其中一条即可,并说明理由.
【我的探究】性质:等腰梯形的同一底上的两个角相等.
③
解:理由:过点C作CE∥DA交AB于点E,
∵AB∥CD,∴四边形AECD是平行四边形,∴AD=EC,AD∥EC,
∵AD=BC,∴EC=BC,∴∠CEB=∠B,
∵AD∥EC,∴∠CEB=∠A,∴∠A=∠B.
∵CD∥AB,∴∠D+∠A=180°,∠BCD+∠B=180°.
∵∠A=∠B,∴∠D=∠BCD.
七、(本题满分12分)
22.我们给出如下定义:有一组相邻内角相等的四边形叫做等邻角四边形.请解答下列问题.
(1)写出一个你所学过的特殊四边形中是等邻角四边形的图形的名称;
(2)如图①,在△ABC中,AB=AC,点D在BC上,且CD=AC,E,F分别为BC,AD的中点,连接EF并延长交AB于点G.求证:四边形AGEC是等邻角四边形;
(3)如图②,若点D在△ABC的内部,(2)中的其他条件不变,EF交CD于点H,图中是否存在等邻角四边形?若存在,指出是哪个四边形,不必证明;若不存在,请说明理由.
题图
(1)解:答案不唯一,如矩形或正方形.
(2)证明:如答图,连接AE,设∠B的度数为x,
∵AB=AC,CD=AC,BE=CE,
∴∠C=∠B=x,∠1==90°-,AE⊥BC.
∵F是AD的中点,∴AF=DF=EF=AD,∴∠2=∠1=90°-,
∴∠AGE=∠B+∠2=x+90°-=90°+,
∠GEC=180°-=90°+,
∴∠AGE=∠GEC,∴四边形AGEC是等邻角四边形.
(3)解:图②中存在等邻角四边形,四边形AGHC是等邻角四边形.
八、(本题满分14分)
23.如图,已知△ABC和△DEF是两个边长都为1 cm的等边三角形,且点B,D,C,E都在同一直线上,连接AD,CF.
(1)求证:四边形ADFC是平行四边形;
(2)若BD=0.3 cm,△ABC沿着BE的方向以每秒1 cm的速度运动,设△ABC运动的时间为t秒.
①当t为何值时,四边形ADFC是菱形?请说明理由;
②四边形ADFC有可能是矩形吗?若可能,求出t的值及此矩形的面积;若不可能,请说明理由.
题图
答图
(1)证明:∵△ABC和△DEF是两个边长都为1 cm的等边三角形,
∴AC=DF=1 cm,∠ACB=∠FDE=60°,∴AC∥DF,
∴四边形ADFC是平行四边形.
(2)解:①当t=0.3时,四边形ADFC是菱形,理由:∵△ABC沿着BE的方向以每秒1 cm的速度运动,
∴当t==0.3时,点B与点D重合,如答图①所示,则AD=AE=BC=DE=DF=EF,
∴四边形ADFC是菱形.
②有可能.若四边形ADFC是矩形,则∠ADF=90°,如答图②,
∴∠ADC=90°-60°=30°.同理∠DAB=30°=∠ADC,∴BA=BD.同理EC=EF,∴点E与点B重合,
∴t=(1+0.3)÷1=1.3.此时,在Rt△ADF中,∠ADF=90°,DF=1 cm,AF=2 cm,
∴AD===(cm),∴矩形ADFC的面积=AD·DF= cm2.
即当t为1.3时,四边形ADFC是矩形,此矩形的面积为 cm2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
