湘教版七年级数学下册 名校优选精练 第六章《数据的分析》检测题(含答案)
文档属性
| 名称 | 湘教版七年级数学下册 名校优选精练 第六章《数据的分析》检测题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-16 12:09:03 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
湘教版七年级数学下册 名校优选精练 第六章检测题
(时间:120分钟,满分:120分)
班级: 姓名: 成绩: .
一、选择题(每小题3分,共36分)
1.10名学生的平均成绩是x,如果另外5名学生每人得84分,那么整个组的平均成绩是( )
A.分 B.分
C.分 D.分
2.某公司欲招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如下表:
候选人 甲 乙 丙 丁
测试成绩(百分制)
面试 86 92 90 83
笔试 90 83 83 92
如果公司认为,作为公关人员面试的成绩应该比笔试的成绩更重要,并分别赋予它们0.6和0.4的权数.根据四人各自的平均成绩,公司将录取( )
A.甲 B.乙 C.丙 D.丁
3.(宿迁中考)一组数据5,4,2,5,6的中位数是( )
A.5 B.4 C.2 D.6
4.(丹东中考)一组数据8,3,8,6,7,8,7的众数和中位数分别是( )
A.8,6 B.7,6 C.7,8 D.8,7
5.(内江中考)某校有25名同学参加某比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道了自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的( )
A.最高分 B.中位数 C.方差 D.平均数
6.某居民小区开展节约用电活动,该小区100户家庭4月份的节电情况如下表所示:
节电量(千瓦时) 20 30 40 50
户数(户) 20 30 30 20
那么4月份这100户家庭的节电量(单位:千瓦时)的平均数是( )
A.35 B.26 C.25 D.20
7.今年6月某日部分区县的最高气温(单位:℃)如下表:
区县 大兴 通州 平谷 顺义 怀柔 门头沟 延庆 昌平 密云 房山
最高气温 32 32 30 32 30 32 29 32 30 32
其最高气温的众数与中位数分别是( )
A.32,32 B.32,30 C.30,32 D.32,31
8.(连云港中考)某校要从四名学生中选拔一名参加市“风华小主播”大赛,选拔赛中每名学生的平均成绩x及其方差s2如下表所示,如果要选择一名成绩高且发挥稳定的学生参赛,则应选择的学生是( )
甲 乙 丙 丁
x 8 9 9 8
s2 1 1 1.2 1.3
A.甲 B.乙 C.丙 D.丁
9.某次知识竞赛中,10名学生的成绩统计如下:
分数(分) 60 70 80 90 100
人数(人) 1 1 5 2 1
则下列说法正确的是( )
A.学生成绩的方差是4 B.学生成绩的众数是5
C.学生成绩的中位数是80分 D.学生成绩的平均分是80分
10.若数据x1、x2、x3、x4、x5的平均数是3,那么数据x1-2,x2+2,x3+4,x4+6,x5-5的平均数是( )
A.3 B.2 C.5 D.4
11.一组数据2,3,4,x中,若中位数与平均数相等,则数x不可能是 ( )
A.1 B.2 C.3 D.5
12.如果一组数据a1,a2,…,an的方差是2,那么一组新数据2a1,2a2,…,2an的方差是( )
A.2 B.4 C.8 D.16
二、填空题(每小题3分,共18分)
13.(东营中考)某学习小组有8人,在一次数学测验中的成绩分别是:102,115,100,105,92,105,85,104,则他们成绩 的平均数是 .
14.(牡丹江中考)若四个互不相等的正整数中,最大的数是8,中位数是4,则这四个数的和为 .
15.(金华中考)为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5 mg/L,则第3次检测得到的氨氮含量是 mg/L.
16.某次跳绳比赛中,统计甲、乙两班学生每分钟跳绳的成绩(单位:次)情况如下表,有三个命题:①甲班平均成绩低于乙班平均成绩;②甲班成绩的波动比乙班成绩的波动大;③甲班成绩优秀人数少于乙班成绩优秀人数(跳绳次数≥150次为优秀).其中正确的命题是 .(只填序号)
班级 参加人数 平均次数 中位数 方差
甲班 45 135 149 180
乙班 45 135 151 130
17.若一组数据1,2,x,4的众数是1,则这组数据的方差为 .
18.已知数据x1,x2,x3,…,xn的平均数为5,方差为8,那么数据ax1-b,ax2-b,ax3-b,…,axn-b的平均数是 ,方差是 .
三、解答题(共66分)
19.(8分)下表是某校七(1)班20名学生某次数学测试的成绩统计表:
成绩(分) 60 70 80 90 100
人数(个) 1 5 x y 2
(1)若这20名学生成绩的平均数为82分,求x和y的值;
(2)在(1)的条件下,设这20名学生本次测验成绩的众数为a分,中位数为b分,求a和b的值.
20.(8分)题中给出的条形图是截止到2021年44位费尔兹奖得主获奖的年龄统计图,经计算费尔兹奖得主获奖时的平均年龄约是35岁.
根据条形图回答问题:
(1)费尔兹奖得主获奖时的年龄超过中位数的有多少人?
(2)费尔兹奖得主获奖时的年龄高于平均年龄的人数占获奖总人数的百分比是多少?
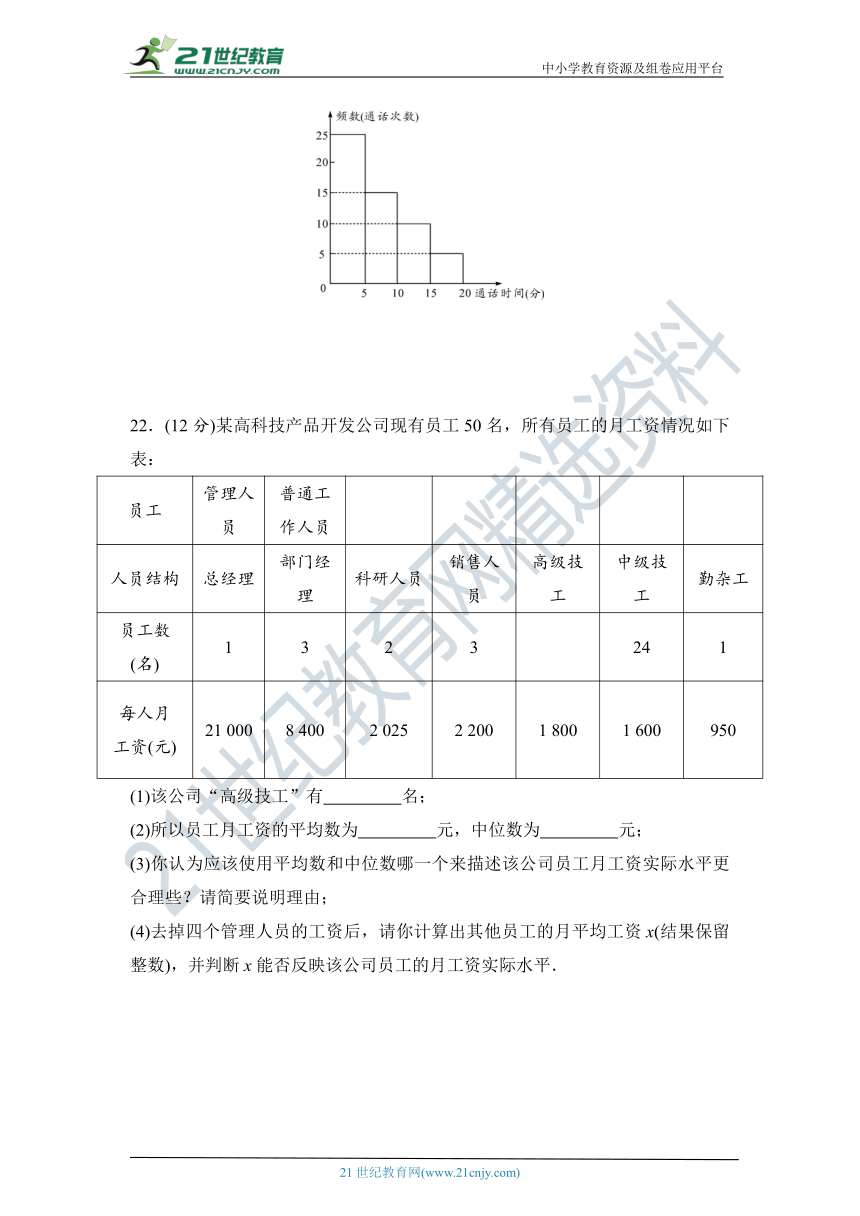
21.(8分)江涛同学统计了他家10月份的电话清单,按通话时间画出直方图,从左到右分别为一、二、三、四组,如图所示.
(1)他家这个月总的通话次数为 次,通话时间的中位数落在第 组内;
(2)求通话时间不足10分钟的通话次数占总通话次数的百分率.(结果精确到1%)
22.(12分)某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员工 管理人员 普通工作人员
人员结构 总经理 部门经理 科研人员 销售人员 高级技工 中级技工 勤杂工
员工数(名) 1 3 2 3 24 1
每人月工资(元) 21 000 8 400 2 025 2 200 1 800 1 600 950
(1)该公司“高级技工”有 名;
(2)所以员工月工资的平均数为 元,中位数为 元;
(3)你认为应该使用平均数和中位数哪一个来描述该公司员工月工资实际水平更合理些?请简要说明理由;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资x(结果保留整数),并判断x能否反映该公司员工的月工资实际水平.
23.(10分)(自贡中考)我市开展“美丽自贡,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;
(2)扇形图中的“1.5小时”部分圆心角是多少度?
(3)求抽查的学生劳动时间的众数、中位数.
24.(10分)(吉林中考)要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.
(1)已求得甲的平均成绩为8环,求乙的平均成绩;
(2)观察图形,直接写出甲、乙这10次射击成绩的方差s,s哪个大;
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选 参赛更合适,如果其他班级参赛选手的射击成绩在9环左右,本班应该选 参赛更合适.
25.(10分)某校举行“做文明郴州人”演讲比赛,聘请了10位评委为参赛选手打分,赛前组委会拟定了四种记分方案:
方案一:取所有评委所给的平均分;
方案二:在所有评委给的分中,去掉一个最高分,去掉一个最低分,取剩余得分的平均分;
方案三:取所有评委给分的中位数;
方案四:取所有评委给分的众数.
为了探究四种记分方案的合理性,先让一名表演选手(不参加正式比赛的)演讲,让10位评委给演讲者评分,表演者得分如下表:
评委编号 1 2 3 4 5 6 7 8 9 10
打分 7.0 7.8 3.2 8.0 8.4 8.4 9.8 8.0 8.4 8.0
(1)请分别用上述四种方案计算表演者的得分;
(2)如果你是评委会成员,你会建议采用哪种可行的记分方案?你觉得哪几种方案不合适?
参考答案
一、选择题(每小题3分,共36分)
1.10名学生的平均成绩是x,如果另外5名学生每人得84分,那么整个组的平均成绩是(B)
A.分 B.分
C.分 D.分
2.某公司欲招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如下表:
候选人 甲 乙 丙 丁
测试成绩(百分制)
面试 86 92 90 83
笔试 90 83 83 92
如果公司认为,作为公关人员面试的成绩应该比笔试的成绩更重要,并分别赋予它们0.6和0.4的权数.根据四人各自的平均成绩,公司将录取(B)
A.甲 B.乙 C.丙 D.丁
3.(宿迁中考)一组数据5,4,2,5,6的中位数是 (A)
A.5 B.4 C.2 D.6
4.(丹东中考)一组数据8,3,8,6,7,8,7的众数和中位数分别是(D)
A.8,6 B.7,6 C.7,8 D.8,7
5.(内江中考)某校有25名同学参加某比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道了自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的 (B)
A.最高分 B.中位数 C.方差 D.平均数
6.某居民小区开展节约用电活动,该小区100户家庭4月份的节电情况如下表所示:
节电量(千瓦时) 20 30 40 50
户数(户) 20 30 30 20
那么4月份这100户家庭的节电量(单位:千瓦时)的平均数是(A)
A.35 B.26 C.25 D.20
7.今年6月某日部分区县的最高气温(单位:℃)如下表:
区县 大兴 通州 平谷 顺义 怀柔 门头沟 延庆 昌平 密云 房山
最高气温 32 32 30 32 30 32 29 32 30 32
其最高气温的众数与中位数分别是 (A)
A.32,32 B.32,30 C.30,32 D.32,31
8.(连云港中考)某校要从四名学生中选拔一名参加市“风华小主播”大赛,选拔赛中每名学生的平均成绩x及其方差s2如下表所示,如果要选择一名成绩高且发挥稳定的学生参赛,则应选择的学生是 (B)
甲 乙 丙 丁
x 8 9 9 8
s2 1 1 1.2 1.3
A.甲 B.乙 C.丙 D.丁
9.某次知识竞赛中,10名学生的成绩统计如下:
分数(分) 60 70 80 90 100
人数(人) 1 1 5 2 1
则下列说法正确的是(C)
A.学生成绩的方差是4 B.学生成绩的众数是5
C.学生成绩的中位数是80分 D.学生成绩的平均分是80分
10.若数据x1、x2、x3、x4、x5的平均数是3,那么数据x1-2,x2+2,x3+4,x4+6,x5-5的平均数是 (D)
A.3 B.2 C.5 D.4
11.一组数据2,3,4,x中,若中位数与平均数相等,则数x不可能是(B)
A.1 B.2 C.3 D.5
12.如果一组数据a1,a2,…,an的方差是2,那么一组新数据2a1,2a2,…,2an的方差是(C)
A.2 B.4 C.8 D.16
二、填空题(每小题3分,共18分)
13.(东营中考)某学习小组有8人,在一次数学测验中的成绩分别是:102,115,100,105,92,105,85,104,则他们成绩 的平均数是__101__.
14.(牡丹江中考)若四个互不相等的正整数中,最大的数是8,中位数是4,则这四个数的和为__17或18__.
15.(金华中考)为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5 mg/L,则第3次检测得到的氨氮含量是__1__mg/L.
16.某次跳绳比赛中,统计甲、乙两班学生每分钟跳绳的成绩(单位:次)情况如下表,有三个命题:①甲班平均成绩低于乙班平均成绩;②甲班成绩的波动比乙班成绩的波动大;③甲班成绩优秀人数少于乙班成绩优秀人数(跳绳次数≥150次为优秀).其中正确的命题是__②③__.(只填序号)
班级 参加人数 平均次数 中位数 方差
甲班 45 135 149 180
乙班 45 135 151 130
17.若一组数据1,2,x,4的众数是1,则这组数据的方差为__1.5__.
18.已知数据x1,x2,x3,…,xn的平均数为5,方差为8,那么数据ax1-b,ax2-b,ax3-b,…,axn-b的平均数是__5a-b__,方差是__8a2__.
三、解答题(共66分)
19.(8分)下表是某校七(1)班20名学生某次数学测试的成绩统计表:
成绩(分) 60 70 80 90 100
人数(个) 1 5 x y 2
(1)若这20名学生成绩的平均数为82分,求x和y的值;
(2)在(1)的条件下,设这20名学生本次测验成绩的众数为a分,中位数为b分,求a和b的值.
解:(1)由题意得
∴解得
(2)a=90,b=80.
20.(8分)题中给出的条形图是截止到2021年44位费尔兹奖得主获奖的年龄统计图,经计算费尔兹奖得主获奖时的平均年龄约是35岁.
根据条形图回答问题:
(1)费尔兹奖得主获奖时的年龄超过中位数的有多少人?
(2)费尔兹奖得主获奖时的年龄高于平均年龄的人数占获奖总人数的百分比是多少?
解:(1)22人;
(2)50%.
21.(8分)江涛同学统计了他家10月份的电话清单,按通话时间画出直方图,从左到右分别为一、二、三、四组,如图所示.
(1)他家这个月总的通话次数为__55__次,通话时间的中位数落在第__二__组内;
(2)求通话时间不足10分钟的通话次数占总通话次数的百分率.(结果精确到1%)
解:由图可知通话时间不足10分钟的通话次数为:
25+15=40(次),∴×100%≈73%.
22.(12分)某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员工 管理人员 普通工作人员
人员结构 总经理 部门经理 科研人员 销售人员 高级技工 中级技工 勤杂工
员工数(名) 1 3 2 3 24 1
每人月工资(元) 21 000 8 400 2 025 2 200 1 800 1 600 950
(1)该公司“高级技工”有__16__名;
(2)所以员工月工资的平均数为__2_500__元,中位数为__1_700__元;
(3)你认为应该使用平均数和中位数哪一个来描述该公司员工月工资实际水平更合理些?请简要说明理由;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资x(结果保留整数),并判断x能否反映该公司员工的月工资实际水平.
(3)解:使用中位数来描述该公司员工月工资实际水平更合理些,因为少数特殊值影响整体的平均数.
(4)解:x=1 713(元),x能反映该公司员工的月工资实际水平.
23.(10分)(自贡中考)我市开展“美丽自贡,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;
(2)扇形图中的“1.5小时”部分圆心角是多少度?
(3)求抽查的学生劳动时间的众数、中位数.
解:(1)根据题意得:30÷30%=100(人),
∴学生劳动时间为“1.5小时”的人数为100-(12+30+18)=40(人),
补全统计图,如图所示.
(2)根据题意得:40%×360°=144°,
则扇形图中的“1.5小时”部分圆心角是144°;
(3)根据题意得:抽查的学生劳动时间的众数为1.5小时、中位数为1.5小时.
24.(10分)(吉林中考)要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.
(1)已求得甲的平均成绩为8环,求乙的平均成绩;
(2)观察图形,直接写出甲、乙这10次射击成绩的方差s,s哪个大;
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选__乙__参赛更合适,如果其他班级参赛选手的射击成绩在9环左右,本班应该选__甲__参赛更合适.
解:(1)乙的平均成绩是:(8+9+8+8+7+8+9+8+8+7)÷10=8(环).
(2)根据图象可知:甲的波动大于乙的波动,则s>s.
25.(10分)某校举行“做文明郴州人”演讲比赛,聘请了10位评委为参赛选手打分,赛前组委会拟定了四种记分方案:
方案一:取所有评委所给的平均分;
方案二:在所有评委给的分中,去掉一个最高分,去掉一个最低分,取剩余得分的平均分;
方案三:取所有评委给分的中位数;
方案四:取所有评委给分的众数.
为了探究四种记分方案的合理性,先让一名表演选手(不参加正式比赛的)演讲,让10位评委给演讲者评分,表演者得分如下表:
评委编号 1 2 3 4 5 6 7 8 9 10
打分 7.0 7.8 3.2 8.0 8.4 8.4 9.8 8.0 8.4 8.0
(1)请分别用上述四种方案计算表演者的得分;
(2)如果你是评委会成员,你会建议采用哪种可行的记分方案?你觉得哪几种方案不合适?
解:(1)方案一最后得分为:×(7.0+7.8+3.2+3×8.0+3×8.4+9.8)=7.7(分);
方案二最后得分为:×(7.0+7.8+3×8.0+3×8.4)=8(分);
方案三最后得分为:8分;
方案四最后得分为:8分和8.4分.
建议采用方案二或方案三.因为方案一中的平均数受极端数值的影响,所以方案一不适合作为最后得分的方案;因为方案四中的众数有两个,众数失去了实际意义,所以方案四不适合作为最后得分的方案.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
湘教版七年级数学下册 名校优选精练 第六章检测题
(时间:120分钟,满分:120分)
班级: 姓名: 成绩: .
一、选择题(每小题3分,共36分)
1.10名学生的平均成绩是x,如果另外5名学生每人得84分,那么整个组的平均成绩是( )
A.分 B.分
C.分 D.分
2.某公司欲招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如下表:
候选人 甲 乙 丙 丁
测试成绩(百分制)
面试 86 92 90 83
笔试 90 83 83 92
如果公司认为,作为公关人员面试的成绩应该比笔试的成绩更重要,并分别赋予它们0.6和0.4的权数.根据四人各自的平均成绩,公司将录取( )
A.甲 B.乙 C.丙 D.丁
3.(宿迁中考)一组数据5,4,2,5,6的中位数是( )
A.5 B.4 C.2 D.6
4.(丹东中考)一组数据8,3,8,6,7,8,7的众数和中位数分别是( )
A.8,6 B.7,6 C.7,8 D.8,7
5.(内江中考)某校有25名同学参加某比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道了自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的( )
A.最高分 B.中位数 C.方差 D.平均数
6.某居民小区开展节约用电活动,该小区100户家庭4月份的节电情况如下表所示:
节电量(千瓦时) 20 30 40 50
户数(户) 20 30 30 20
那么4月份这100户家庭的节电量(单位:千瓦时)的平均数是( )
A.35 B.26 C.25 D.20
7.今年6月某日部分区县的最高气温(单位:℃)如下表:
区县 大兴 通州 平谷 顺义 怀柔 门头沟 延庆 昌平 密云 房山
最高气温 32 32 30 32 30 32 29 32 30 32
其最高气温的众数与中位数分别是( )
A.32,32 B.32,30 C.30,32 D.32,31
8.(连云港中考)某校要从四名学生中选拔一名参加市“风华小主播”大赛,选拔赛中每名学生的平均成绩x及其方差s2如下表所示,如果要选择一名成绩高且发挥稳定的学生参赛,则应选择的学生是( )
甲 乙 丙 丁
x 8 9 9 8
s2 1 1 1.2 1.3
A.甲 B.乙 C.丙 D.丁
9.某次知识竞赛中,10名学生的成绩统计如下:
分数(分) 60 70 80 90 100
人数(人) 1 1 5 2 1
则下列说法正确的是( )
A.学生成绩的方差是4 B.学生成绩的众数是5
C.学生成绩的中位数是80分 D.学生成绩的平均分是80分
10.若数据x1、x2、x3、x4、x5的平均数是3,那么数据x1-2,x2+2,x3+4,x4+6,x5-5的平均数是( )
A.3 B.2 C.5 D.4
11.一组数据2,3,4,x中,若中位数与平均数相等,则数x不可能是 ( )
A.1 B.2 C.3 D.5
12.如果一组数据a1,a2,…,an的方差是2,那么一组新数据2a1,2a2,…,2an的方差是( )
A.2 B.4 C.8 D.16
二、填空题(每小题3分,共18分)
13.(东营中考)某学习小组有8人,在一次数学测验中的成绩分别是:102,115,100,105,92,105,85,104,则他们成绩 的平均数是 .
14.(牡丹江中考)若四个互不相等的正整数中,最大的数是8,中位数是4,则这四个数的和为 .
15.(金华中考)为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5 mg/L,则第3次检测得到的氨氮含量是 mg/L.
16.某次跳绳比赛中,统计甲、乙两班学生每分钟跳绳的成绩(单位:次)情况如下表,有三个命题:①甲班平均成绩低于乙班平均成绩;②甲班成绩的波动比乙班成绩的波动大;③甲班成绩优秀人数少于乙班成绩优秀人数(跳绳次数≥150次为优秀).其中正确的命题是 .(只填序号)
班级 参加人数 平均次数 中位数 方差
甲班 45 135 149 180
乙班 45 135 151 130
17.若一组数据1,2,x,4的众数是1,则这组数据的方差为 .
18.已知数据x1,x2,x3,…,xn的平均数为5,方差为8,那么数据ax1-b,ax2-b,ax3-b,…,axn-b的平均数是 ,方差是 .
三、解答题(共66分)
19.(8分)下表是某校七(1)班20名学生某次数学测试的成绩统计表:
成绩(分) 60 70 80 90 100
人数(个) 1 5 x y 2
(1)若这20名学生成绩的平均数为82分,求x和y的值;
(2)在(1)的条件下,设这20名学生本次测验成绩的众数为a分,中位数为b分,求a和b的值.
20.(8分)题中给出的条形图是截止到2021年44位费尔兹奖得主获奖的年龄统计图,经计算费尔兹奖得主获奖时的平均年龄约是35岁.
根据条形图回答问题:
(1)费尔兹奖得主获奖时的年龄超过中位数的有多少人?
(2)费尔兹奖得主获奖时的年龄高于平均年龄的人数占获奖总人数的百分比是多少?
21.(8分)江涛同学统计了他家10月份的电话清单,按通话时间画出直方图,从左到右分别为一、二、三、四组,如图所示.
(1)他家这个月总的通话次数为 次,通话时间的中位数落在第 组内;
(2)求通话时间不足10分钟的通话次数占总通话次数的百分率.(结果精确到1%)
22.(12分)某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员工 管理人员 普通工作人员
人员结构 总经理 部门经理 科研人员 销售人员 高级技工 中级技工 勤杂工
员工数(名) 1 3 2 3 24 1
每人月工资(元) 21 000 8 400 2 025 2 200 1 800 1 600 950
(1)该公司“高级技工”有 名;
(2)所以员工月工资的平均数为 元,中位数为 元;
(3)你认为应该使用平均数和中位数哪一个来描述该公司员工月工资实际水平更合理些?请简要说明理由;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资x(结果保留整数),并判断x能否反映该公司员工的月工资实际水平.
23.(10分)(自贡中考)我市开展“美丽自贡,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;
(2)扇形图中的“1.5小时”部分圆心角是多少度?
(3)求抽查的学生劳动时间的众数、中位数.
24.(10分)(吉林中考)要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.
(1)已求得甲的平均成绩为8环,求乙的平均成绩;
(2)观察图形,直接写出甲、乙这10次射击成绩的方差s,s哪个大;
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选 参赛更合适,如果其他班级参赛选手的射击成绩在9环左右,本班应该选 参赛更合适.
25.(10分)某校举行“做文明郴州人”演讲比赛,聘请了10位评委为参赛选手打分,赛前组委会拟定了四种记分方案:
方案一:取所有评委所给的平均分;
方案二:在所有评委给的分中,去掉一个最高分,去掉一个最低分,取剩余得分的平均分;
方案三:取所有评委给分的中位数;
方案四:取所有评委给分的众数.
为了探究四种记分方案的合理性,先让一名表演选手(不参加正式比赛的)演讲,让10位评委给演讲者评分,表演者得分如下表:
评委编号 1 2 3 4 5 6 7 8 9 10
打分 7.0 7.8 3.2 8.0 8.4 8.4 9.8 8.0 8.4 8.0
(1)请分别用上述四种方案计算表演者的得分;
(2)如果你是评委会成员,你会建议采用哪种可行的记分方案?你觉得哪几种方案不合适?
参考答案
一、选择题(每小题3分,共36分)
1.10名学生的平均成绩是x,如果另外5名学生每人得84分,那么整个组的平均成绩是(B)
A.分 B.分
C.分 D.分
2.某公司欲招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如下表:
候选人 甲 乙 丙 丁
测试成绩(百分制)
面试 86 92 90 83
笔试 90 83 83 92
如果公司认为,作为公关人员面试的成绩应该比笔试的成绩更重要,并分别赋予它们0.6和0.4的权数.根据四人各自的平均成绩,公司将录取(B)
A.甲 B.乙 C.丙 D.丁
3.(宿迁中考)一组数据5,4,2,5,6的中位数是 (A)
A.5 B.4 C.2 D.6
4.(丹东中考)一组数据8,3,8,6,7,8,7的众数和中位数分别是(D)
A.8,6 B.7,6 C.7,8 D.8,7
5.(内江中考)某校有25名同学参加某比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道了自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的 (B)
A.最高分 B.中位数 C.方差 D.平均数
6.某居民小区开展节约用电活动,该小区100户家庭4月份的节电情况如下表所示:
节电量(千瓦时) 20 30 40 50
户数(户) 20 30 30 20
那么4月份这100户家庭的节电量(单位:千瓦时)的平均数是(A)
A.35 B.26 C.25 D.20
7.今年6月某日部分区县的最高气温(单位:℃)如下表:
区县 大兴 通州 平谷 顺义 怀柔 门头沟 延庆 昌平 密云 房山
最高气温 32 32 30 32 30 32 29 32 30 32
其最高气温的众数与中位数分别是 (A)
A.32,32 B.32,30 C.30,32 D.32,31
8.(连云港中考)某校要从四名学生中选拔一名参加市“风华小主播”大赛,选拔赛中每名学生的平均成绩x及其方差s2如下表所示,如果要选择一名成绩高且发挥稳定的学生参赛,则应选择的学生是 (B)
甲 乙 丙 丁
x 8 9 9 8
s2 1 1 1.2 1.3
A.甲 B.乙 C.丙 D.丁
9.某次知识竞赛中,10名学生的成绩统计如下:
分数(分) 60 70 80 90 100
人数(人) 1 1 5 2 1
则下列说法正确的是(C)
A.学生成绩的方差是4 B.学生成绩的众数是5
C.学生成绩的中位数是80分 D.学生成绩的平均分是80分
10.若数据x1、x2、x3、x4、x5的平均数是3,那么数据x1-2,x2+2,x3+4,x4+6,x5-5的平均数是 (D)
A.3 B.2 C.5 D.4
11.一组数据2,3,4,x中,若中位数与平均数相等,则数x不可能是(B)
A.1 B.2 C.3 D.5
12.如果一组数据a1,a2,…,an的方差是2,那么一组新数据2a1,2a2,…,2an的方差是(C)
A.2 B.4 C.8 D.16
二、填空题(每小题3分,共18分)
13.(东营中考)某学习小组有8人,在一次数学测验中的成绩分别是:102,115,100,105,92,105,85,104,则他们成绩 的平均数是__101__.
14.(牡丹江中考)若四个互不相等的正整数中,最大的数是8,中位数是4,则这四个数的和为__17或18__.
15.(金华中考)为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5 mg/L,则第3次检测得到的氨氮含量是__1__mg/L.
16.某次跳绳比赛中,统计甲、乙两班学生每分钟跳绳的成绩(单位:次)情况如下表,有三个命题:①甲班平均成绩低于乙班平均成绩;②甲班成绩的波动比乙班成绩的波动大;③甲班成绩优秀人数少于乙班成绩优秀人数(跳绳次数≥150次为优秀).其中正确的命题是__②③__.(只填序号)
班级 参加人数 平均次数 中位数 方差
甲班 45 135 149 180
乙班 45 135 151 130
17.若一组数据1,2,x,4的众数是1,则这组数据的方差为__1.5__.
18.已知数据x1,x2,x3,…,xn的平均数为5,方差为8,那么数据ax1-b,ax2-b,ax3-b,…,axn-b的平均数是__5a-b__,方差是__8a2__.
三、解答题(共66分)
19.(8分)下表是某校七(1)班20名学生某次数学测试的成绩统计表:
成绩(分) 60 70 80 90 100
人数(个) 1 5 x y 2
(1)若这20名学生成绩的平均数为82分,求x和y的值;
(2)在(1)的条件下,设这20名学生本次测验成绩的众数为a分,中位数为b分,求a和b的值.
解:(1)由题意得
∴解得
(2)a=90,b=80.
20.(8分)题中给出的条形图是截止到2021年44位费尔兹奖得主获奖的年龄统计图,经计算费尔兹奖得主获奖时的平均年龄约是35岁.
根据条形图回答问题:
(1)费尔兹奖得主获奖时的年龄超过中位数的有多少人?
(2)费尔兹奖得主获奖时的年龄高于平均年龄的人数占获奖总人数的百分比是多少?
解:(1)22人;
(2)50%.
21.(8分)江涛同学统计了他家10月份的电话清单,按通话时间画出直方图,从左到右分别为一、二、三、四组,如图所示.
(1)他家这个月总的通话次数为__55__次,通话时间的中位数落在第__二__组内;
(2)求通话时间不足10分钟的通话次数占总通话次数的百分率.(结果精确到1%)
解:由图可知通话时间不足10分钟的通话次数为:
25+15=40(次),∴×100%≈73%.
22.(12分)某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员工 管理人员 普通工作人员
人员结构 总经理 部门经理 科研人员 销售人员 高级技工 中级技工 勤杂工
员工数(名) 1 3 2 3 24 1
每人月工资(元) 21 000 8 400 2 025 2 200 1 800 1 600 950
(1)该公司“高级技工”有__16__名;
(2)所以员工月工资的平均数为__2_500__元,中位数为__1_700__元;
(3)你认为应该使用平均数和中位数哪一个来描述该公司员工月工资实际水平更合理些?请简要说明理由;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资x(结果保留整数),并判断x能否反映该公司员工的月工资实际水平.
(3)解:使用中位数来描述该公司员工月工资实际水平更合理些,因为少数特殊值影响整体的平均数.
(4)解:x=1 713(元),x能反映该公司员工的月工资实际水平.
23.(10分)(自贡中考)我市开展“美丽自贡,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;
(2)扇形图中的“1.5小时”部分圆心角是多少度?
(3)求抽查的学生劳动时间的众数、中位数.
解:(1)根据题意得:30÷30%=100(人),
∴学生劳动时间为“1.5小时”的人数为100-(12+30+18)=40(人),
补全统计图,如图所示.
(2)根据题意得:40%×360°=144°,
则扇形图中的“1.5小时”部分圆心角是144°;
(3)根据题意得:抽查的学生劳动时间的众数为1.5小时、中位数为1.5小时.
24.(10分)(吉林中考)要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.
(1)已求得甲的平均成绩为8环,求乙的平均成绩;
(2)观察图形,直接写出甲、乙这10次射击成绩的方差s,s哪个大;
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选__乙__参赛更合适,如果其他班级参赛选手的射击成绩在9环左右,本班应该选__甲__参赛更合适.
解:(1)乙的平均成绩是:(8+9+8+8+7+8+9+8+8+7)÷10=8(环).
(2)根据图象可知:甲的波动大于乙的波动,则s>s.
25.(10分)某校举行“做文明郴州人”演讲比赛,聘请了10位评委为参赛选手打分,赛前组委会拟定了四种记分方案:
方案一:取所有评委所给的平均分;
方案二:在所有评委给的分中,去掉一个最高分,去掉一个最低分,取剩余得分的平均分;
方案三:取所有评委给分的中位数;
方案四:取所有评委给分的众数.
为了探究四种记分方案的合理性,先让一名表演选手(不参加正式比赛的)演讲,让10位评委给演讲者评分,表演者得分如下表:
评委编号 1 2 3 4 5 6 7 8 9 10
打分 7.0 7.8 3.2 8.0 8.4 8.4 9.8 8.0 8.4 8.0
(1)请分别用上述四种方案计算表演者的得分;
(2)如果你是评委会成员,你会建议采用哪种可行的记分方案?你觉得哪几种方案不合适?
解:(1)方案一最后得分为:×(7.0+7.8+3.2+3×8.0+3×8.4+9.8)=7.7(分);
方案二最后得分为:×(7.0+7.8+3×8.0+3×8.4)=8(分);
方案三最后得分为:8分;
方案四最后得分为:8分和8.4分.
建议采用方案二或方案三.因为方案一中的平均数受极端数值的影响,所以方案一不适合作为最后得分的方案;因为方案四中的众数有两个,众数失去了实际意义,所以方案四不适合作为最后得分的方案.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
