八年级数学下册同步精品课件(沪科版)19.2.4三角形的中位线 课件(共33张PPT)
文档属性
| 名称 | 八年级数学下册同步精品课件(沪科版)19.2.4三角形的中位线 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 527.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-17 10:17:31 | ||
图片预览





文档简介
(共33张PPT)
19.2.4 三角形的中位线
知识回顾
A
B
D
C
O
平行四边形的对边平行
平行四边形的对角相等,
且相等.
邻角互补.
平行四边形的
对角线
互相平分
对角线的性质
平行四边形有哪些性质?
边的性质
角的性质
从边来判定
平行四边形的判定方法
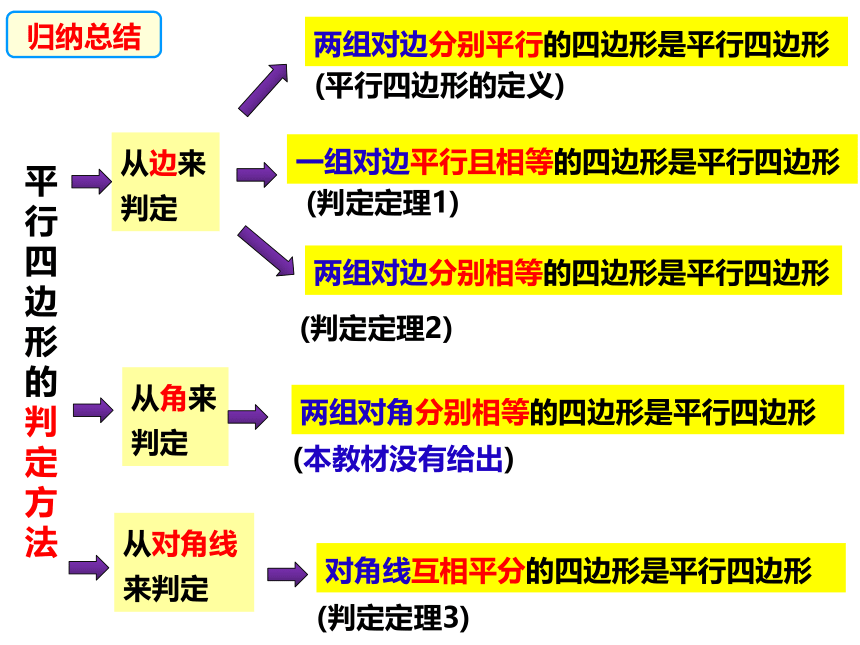
归纳总结
从角来判定
从对角线来判定
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
(平行四边形的定义)
(判定定理1)
两组对边分别相等的四边形是平行四边形
(判定定理2)
两组对角分别相等的四边形是平行四边形
(本教材没有给出)
对角线互相平分的四边形是平行四边形
(判定定理3)
探究新知
如图,l1∥l2,l4∥l5,两组平行线相交得到四边形 ABB1A1.
(1) 图中有哪些相等的线段?为什么?
平行四边形ABB1A1
l1
l2
l4
A
B
A1
B1
l5
AA1=BB1
AB=A1B1
探究新知
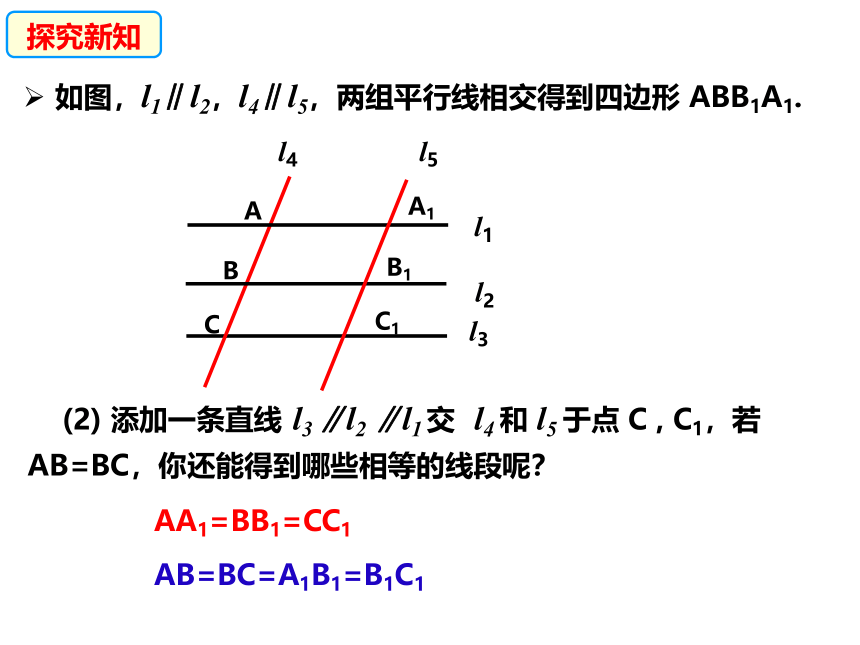
(2) 添加一条直线 l3 ∥l2 ∥l1 交 l4 和 l5 于点 C , C1,若AB=BC,你还能得到哪些相等的线段呢?
l3
C
C1
AA1=BB1=CC1
AB=BC=A1B1=B1C1
l1
l2
l4
A
B
A1
B1
l5
如图,l1∥l2,l4∥l5,两组平行线相交得到四边形 ABB1A1.
探究新知
l1
l2
l4
A
B
A1
B1
l5
l3
C
C1
(3) 将直线 l4 旋转至如图位置,若 AB=BC,你还能得到哪些相等的线段呢?
A1
B1
l5
C1
A1B1=B1C1
你能证明吗?
E
F
过点 B1 作 EF∥ AC,分别交直线 l1、l3 于点 E、F.
如图,l1∥l2,l4∥l5,两组平行线相交得到四边形 ABB1A1.
归纳总结
l1
l2
l3
A
B
C
A1
B1
C1
由此得到如下结论:
那么在其他直线上截得的线段也相等.
如果一组平行线
在一条直线上
截得的线段相等,
平行线等分线段定理:
∵ l1∥l2∥l3 ,
AB=BC
∴ A1B1=B1C1
【几何语言】
如图,l1∥l2,l4∥l5 ,两组平行线相交得到四边形 ABB1A1.
l1
l2
l4
A
B
l3
C
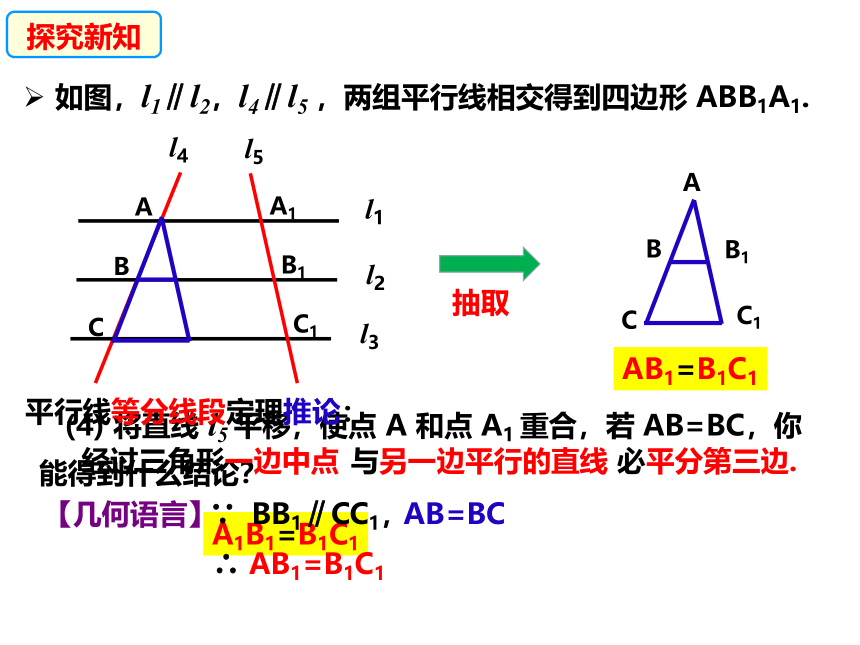
(4) 将直线 l5 平移,使点 A 和点 A1 重合,若 AB=BC,你能得到什么结论?
探究新知
l5
A1
B1
C1
A1B1=B1C1
抽取
A
B
C
B1
C1
AB1=B1C1
平行线等分线段定理推论:
经过三角形一边中点
与另一边平行的直线
必平分第三边.
∵ BB1∥CC1,
AB=BC
∴ AB1=B1C1
【几何语言】
对应练习
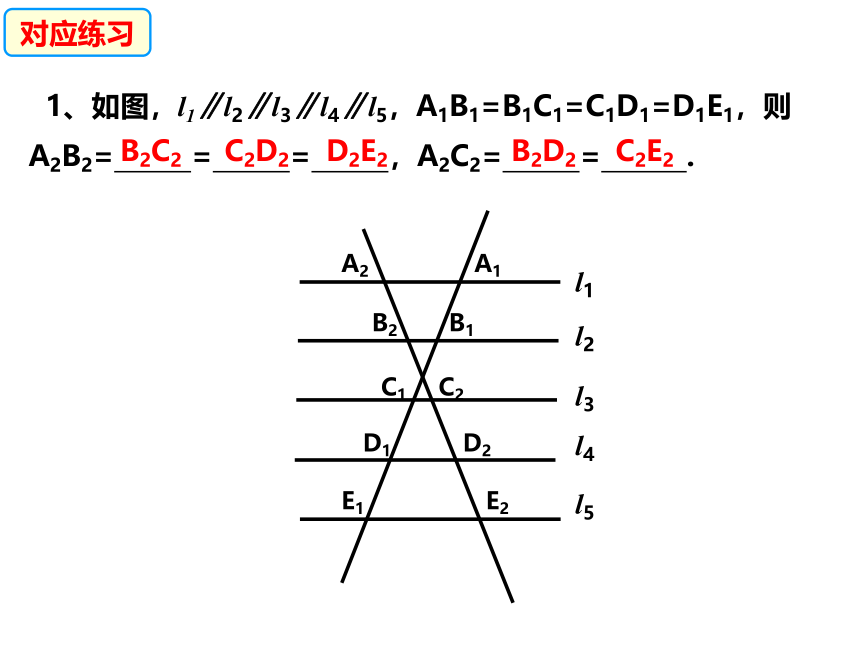
1、如图,l1∥l2∥l3∥l4∥l5,A1B1=B1C1=C1D1=D1E1,则A2B2= = = ,A2C2= = .
l1
l2
l3
A1
B1
C1
l4
l5
D1
E1
A2
B2
C2
D2
E2
B2C2
C2D2
D2E2
B2D2
C2E2
对应练习
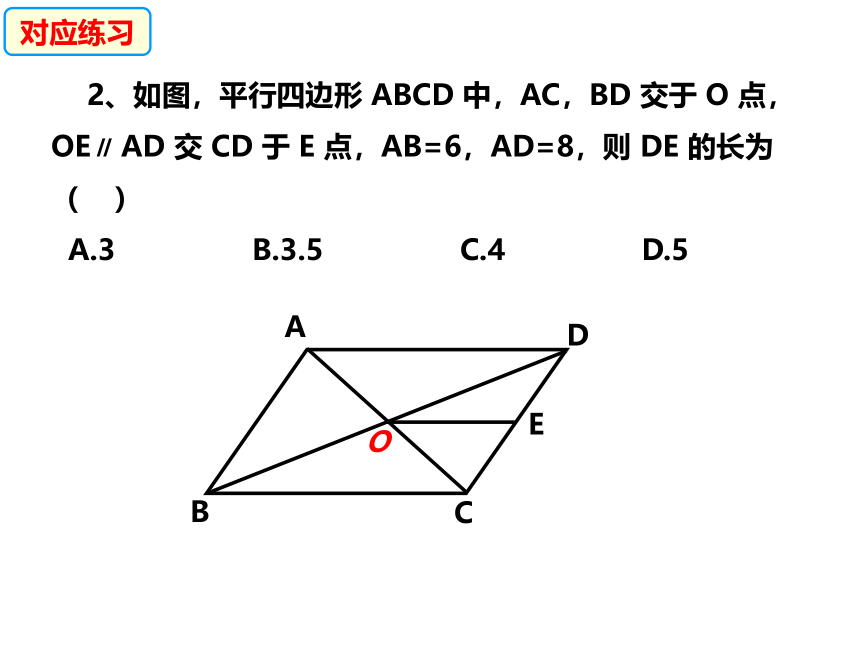
2、如图,平行四边形 ABCD 中,AC,BD 交于 O 点,OE∥ AD 交 CD 于 E 点,AB=6,AD=8,则 DE 的长为( )
A.3 B.3.5 C.4 D.5
B
C
A
E
O
D
探究新知
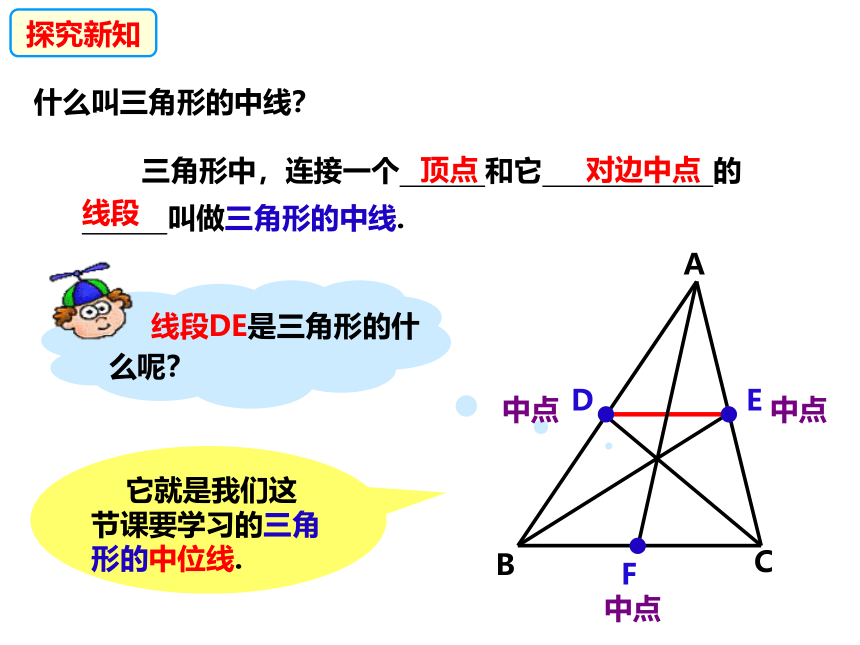
三角形中,连接一个 和它 的
叫做三角形的中线.
线段DE是三角形的什么呢?
它就是我们这节课要学习的三角形的中位线.
顶点
对边中点
线段
A
B
C
F
E
D
中点
中点
中点
什么叫三角形的中线?
概念学习
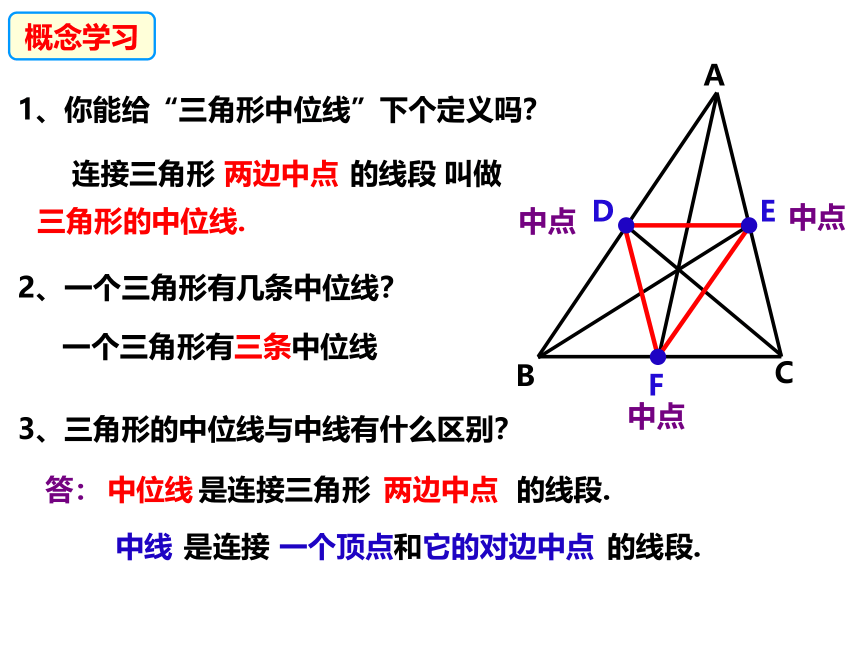
2、一个三角形有几条中位线?
1、你能给“三角形中位线”下个定义吗?
A
B
C
F
E
D
中点
中点
中点
连接三角形
两边中点
的线段
叫做
三角形的中位线.
一个三角形有三条中位线
3、三角形的中位线与中线有什么区别?
答:
中线
中位线
是连接三角形
是连接
两边中点
的线段.
一个顶点和它的对边中点
的线段.
理解定义
A
B
C
E
D
中点
中点
连接三角形
两边中点
的线段
叫做
三角形的中位线.
AE=CE
∴ DE是△ABC的中位线
【几何语言】
∵ AD=BD,
反过来
∴ AD=BD,
∵ DE是△ABC的中位线
AE=CE
观察猜想
在△ABC中,中位线 DE 和边 BC 什么关系
DE和边BC关系
数量关系:
位置关系:
DE=
A
B
C
E
D
1
2
DE∥ BC
BC
三角形
猜想:
你能证明吗?
并且等于等三边的一半
两边中点的连线
平行于第三边,
A
B
C
E
D
E′
证明:
∵ D 为 AB 边上的中点,且 DE′∥ BC
∴ E' 是 AC 的中点
∴ 点 E' 与点 E 重合
过点 D 作 DE′∥ BC 交 AC 于点 E′.
F
验证猜想
求证:
已知:如图,点 D,E 分别为 △ABC 的边 AB,AC 的中点.
DE=
1
2
DE∥ BC,
BC
且
同理,过点 D 作 DF∥AC 交 BC 于点 F
∴ 四边形 DFCE 是平行四边形
∴ DE // BC
则点 F 为 BC 的中点.
∴ DE=FC
= BC
验证猜想
求证:
已知:如图,点D,E分别为△ABC的边AB,AC的中点.
DE=
1
2
DE∥ BC,
BC
且
A
B
C
E
D
连结CF.
证明:
延长DE到F,
使 EF=DE,
F
在△ADE和△CFE中
∵
AE=CE
∠AED=∠CEF
DE=EF
∴ △ADE≌△CFE
(SAS)
∵ 点D,E分别为△ABC的边AB,AC的中点
∴ AE=CE,
∴ AD=CF,
∠A=∠ECF
∴ 四边形BCFD是平行四边形
∴ DF BC
∴ BD=CF,
AB∥ CF
AD=BD
∴
DE∥ BC,
且
DE=
DF
1
2
= BC
1
2
证明:
延长DE到F,使
连接AF , CF , DC.
∵ AE=CE,
∴ 四边形ADCF是平行四边形
∴ 四边形BCFD是平行四边形
A
B
C
E
D
F
求证:
已知:如图,点D,E分别为△ABC的边AB,AC的中点.
DE=
1
2
DE∥ BC,
BC
且
验证猜想
EF=DE
∴ AD CF
∴ BD CF
∴ DF BC
∴
DE∥ BC,
DE=EF
且
DE=
DF
1
2
= BC
1
2
(数量关系)
(位置关系)
主要用途:
(2) 证明一条线段是另一条线段的2倍 或
三角形两边中点的连线平行于第三边,并且等于等三边的一半
归纳总结
三角形中位线定理:
∵ DE是△ABC的中位线
∴ DE∥ BC,
【几何语言】
(或 AD=BD,AE=CE)
且
DE=
BC
1
2
(1) 证明两条线段平行
1
2
A
B
C
E
D
1、如图,在 ABCD中,AC 与 BD 相交于点 O,点 E 是边 AB 的中点,且 AD=10cm,则 OE 的长是 .
5cm
对应练习
B
C
A
D
O
E
2、如图,D,E, F 分别是 △ABC 三边的中点你能发现△DEF 的面积与 △ABC 的面积有什么关系吗 为什么
●
●
●
A
B
C
D
E
F
原三角形面积的 .
因而每个小三角形的面积为
知识拓展:
三角形的三条中位线
把原三角形
分成了4个全等的小三角形,
1
4
变式:如图,点 D,E,F 分别是 △ABC 各边的中点,若 △ABC 的面积为 20 cm2,则 △DEF的面积 .
A
B
C
F
E
D
5cm2
3、如图,点 D,E,F 分别是 △ABC 各边的中点,若△ABC的周长为 10 cm,求 △DEF 的周长?
对应练习
A
B
C
F
E
D
解:
∵ D,E分别是AB、BC的中点
∴ DE是△ABC的中位线
DE=
BC
1
2
∴
同理可得
DF=
AC,
2
1
EF=
AB
1
2
∴ △DEF的周长为
DE+DF+EF=
BC
1
2
+ AC
1
2
+ AB
1
2
(BC+AC+AB)
1
2
=5(cm)
=
每个小三角形的面积为
每个小三角形的周长为
方法技巧:
三角形的三条中位线
把原三角形
分成了4个全等的小三角形,
原三角形周长的 ,
1
2
原三角形面积的 .
1
4
C
A
B
D
F
E
G
H
I
变式练习:如下图,D、E、F、G、H、I 都是各自所在线段的中点,若 △GHI 的周长是 5 cm,则 △ABC 的周长是 cm.
20
4、已知:如图,在四边形 ABCD 中,E、F、G、H 分别是 AB、BC、CD、DA 的中点. 求证:四边形 EFGH 是平行四边形.
A
B
C
D
E
F
G
H
5、如图四边形 ABCD,点 E、F、G、H 分别是边 AB、BC、CD、DA 的中点,连接 EF、FG、GH、HE,得到四边形 EFGH,求证:四边形 EFGH 是平行四边形.
变式:如图所示,点 O 是 △ABC 内一点,D,E,F,G 分别为 AB,AC,OC,OB 的中点.若 OB⊥OC,OA=6,OC=3,OB=4,求四边形 DEFG 的周长.
76、如图,在四边形 ABCD 中,AD=BC,点 P 是对角线BD 的中点,点 E、F 分别是边 CD 和 AB 的中点,若 ∠PEF=30°,则下列说法错误的是( )
A.PE=PF B.∠EPF=120°
C.AD+BC>2EF D.AB+DC>2DB
7、 如图:如果AD= AC,AE= AB,DE=2cm,
那么BC= cm.
A
B
D
C
E
H
G
8
巩固练习
8、已知:如图,△ABC 是锐角三角形. 分别以 AB,AC 为边向外侧作两个等边△ABM和 △CAN. D,E,F 分别是 MB,BC,CN 的中点,连结 DE,EF. 求证:DE=EF
A
B
C
D
E
F
N
M
9、已知:AD 是 △ABC 的中线,点 E 是AD的中点,点 F 是 BE 延长线与 AC 的交点,求证:AF=FC.
G
本节课你有什么收获?
连接三角形
两边中点
的线段
叫做
三角形的中位线.
① 三角形中位线的定义
三角形两边中点的连线平行于第三边,并且等于等三边的一半
② 三角形中位线定理:
(数量关系)
(位置关系)
主要用途:
(2) 证明一条线段是另一条线段的2倍 或
∵ DE是△ABC的中位线
∴ DE∥ BC,
【几何语言】
(或 AD=BD,AE=CE)
且
DE=
BC
1
2
(1) 证明两条线段平行
1
2
A
B
C
E
D
那么在其他直线上截得的线段也相等.
如果一组平行线
在一条直线上
截得的线段相等,
③ 平行线等分线段定理
l1
l2
l4
A
B
l3
C
l5
A1
B1
C1
平行线等分线段定理推论:
经过三角形一边中点
与另一边平行的直线
必平分第三边.
19.2.4 三角形的中位线
知识回顾
A
B
D
C
O
平行四边形的对边平行
平行四边形的对角相等,
且相等.
邻角互补.
平行四边形的
对角线
互相平分
对角线的性质
平行四边形有哪些性质?
边的性质
角的性质
从边来判定
平行四边形的判定方法
归纳总结
从角来判定
从对角线来判定
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
(平行四边形的定义)
(判定定理1)
两组对边分别相等的四边形是平行四边形
(判定定理2)
两组对角分别相等的四边形是平行四边形
(本教材没有给出)
对角线互相平分的四边形是平行四边形
(判定定理3)
探究新知
如图,l1∥l2,l4∥l5,两组平行线相交得到四边形 ABB1A1.
(1) 图中有哪些相等的线段?为什么?
平行四边形ABB1A1
l1
l2
l4
A
B
A1
B1
l5
AA1=BB1
AB=A1B1
探究新知
(2) 添加一条直线 l3 ∥l2 ∥l1 交 l4 和 l5 于点 C , C1,若AB=BC,你还能得到哪些相等的线段呢?
l3
C
C1
AA1=BB1=CC1
AB=BC=A1B1=B1C1
l1
l2
l4
A
B
A1
B1
l5
如图,l1∥l2,l4∥l5,两组平行线相交得到四边形 ABB1A1.
探究新知
l1
l2
l4
A
B
A1
B1
l5
l3
C
C1
(3) 将直线 l4 旋转至如图位置,若 AB=BC,你还能得到哪些相等的线段呢?
A1
B1
l5
C1
A1B1=B1C1
你能证明吗?
E
F
过点 B1 作 EF∥ AC,分别交直线 l1、l3 于点 E、F.
如图,l1∥l2,l4∥l5,两组平行线相交得到四边形 ABB1A1.
归纳总结
l1
l2
l3
A
B
C
A1
B1
C1
由此得到如下结论:
那么在其他直线上截得的线段也相等.
如果一组平行线
在一条直线上
截得的线段相等,
平行线等分线段定理:
∵ l1∥l2∥l3 ,
AB=BC
∴ A1B1=B1C1
【几何语言】
如图,l1∥l2,l4∥l5 ,两组平行线相交得到四边形 ABB1A1.
l1
l2
l4
A
B
l3
C
(4) 将直线 l5 平移,使点 A 和点 A1 重合,若 AB=BC,你能得到什么结论?
探究新知
l5
A1
B1
C1
A1B1=B1C1
抽取
A
B
C
B1
C1
AB1=B1C1
平行线等分线段定理推论:
经过三角形一边中点
与另一边平行的直线
必平分第三边.
∵ BB1∥CC1,
AB=BC
∴ AB1=B1C1
【几何语言】
对应练习
1、如图,l1∥l2∥l3∥l4∥l5,A1B1=B1C1=C1D1=D1E1,则A2B2= = = ,A2C2= = .
l1
l2
l3
A1
B1
C1
l4
l5
D1
E1
A2
B2
C2
D2
E2
B2C2
C2D2
D2E2
B2D2
C2E2
对应练习
2、如图,平行四边形 ABCD 中,AC,BD 交于 O 点,OE∥ AD 交 CD 于 E 点,AB=6,AD=8,则 DE 的长为( )
A.3 B.3.5 C.4 D.5
B
C
A
E
O
D
探究新知
三角形中,连接一个 和它 的
叫做三角形的中线.
线段DE是三角形的什么呢?
它就是我们这节课要学习的三角形的中位线.
顶点
对边中点
线段
A
B
C
F
E
D
中点
中点
中点
什么叫三角形的中线?
概念学习
2、一个三角形有几条中位线?
1、你能给“三角形中位线”下个定义吗?
A
B
C
F
E
D
中点
中点
中点
连接三角形
两边中点
的线段
叫做
三角形的中位线.
一个三角形有三条中位线
3、三角形的中位线与中线有什么区别?
答:
中线
中位线
是连接三角形
是连接
两边中点
的线段.
一个顶点和它的对边中点
的线段.
理解定义
A
B
C
E
D
中点
中点
连接三角形
两边中点
的线段
叫做
三角形的中位线.
AE=CE
∴ DE是△ABC的中位线
【几何语言】
∵ AD=BD,
反过来
∴ AD=BD,
∵ DE是△ABC的中位线
AE=CE
观察猜想
在△ABC中,中位线 DE 和边 BC 什么关系
DE和边BC关系
数量关系:
位置关系:
DE=
A
B
C
E
D
1
2
DE∥ BC
BC
三角形
猜想:
你能证明吗?
并且等于等三边的一半
两边中点的连线
平行于第三边,
A
B
C
E
D
E′
证明:
∵ D 为 AB 边上的中点,且 DE′∥ BC
∴ E' 是 AC 的中点
∴ 点 E' 与点 E 重合
过点 D 作 DE′∥ BC 交 AC 于点 E′.
F
验证猜想
求证:
已知:如图,点 D,E 分别为 △ABC 的边 AB,AC 的中点.
DE=
1
2
DE∥ BC,
BC
且
同理,过点 D 作 DF∥AC 交 BC 于点 F
∴ 四边形 DFCE 是平行四边形
∴ DE // BC
则点 F 为 BC 的中点.
∴ DE=FC
= BC
验证猜想
求证:
已知:如图,点D,E分别为△ABC的边AB,AC的中点.
DE=
1
2
DE∥ BC,
BC
且
A
B
C
E
D
连结CF.
证明:
延长DE到F,
使 EF=DE,
F
在△ADE和△CFE中
∵
AE=CE
∠AED=∠CEF
DE=EF
∴ △ADE≌△CFE
(SAS)
∵ 点D,E分别为△ABC的边AB,AC的中点
∴ AE=CE,
∴ AD=CF,
∠A=∠ECF
∴ 四边形BCFD是平行四边形
∴ DF BC
∴ BD=CF,
AB∥ CF
AD=BD
∴
DE∥ BC,
且
DE=
DF
1
2
= BC
1
2
证明:
延长DE到F,使
连接AF , CF , DC.
∵ AE=CE,
∴ 四边形ADCF是平行四边形
∴ 四边形BCFD是平行四边形
A
B
C
E
D
F
求证:
已知:如图,点D,E分别为△ABC的边AB,AC的中点.
DE=
1
2
DE∥ BC,
BC
且
验证猜想
EF=DE
∴ AD CF
∴ BD CF
∴ DF BC
∴
DE∥ BC,
DE=EF
且
DE=
DF
1
2
= BC
1
2
(数量关系)
(位置关系)
主要用途:
(2) 证明一条线段是另一条线段的2倍 或
三角形两边中点的连线平行于第三边,并且等于等三边的一半
归纳总结
三角形中位线定理:
∵ DE是△ABC的中位线
∴ DE∥ BC,
【几何语言】
(或 AD=BD,AE=CE)
且
DE=
BC
1
2
(1) 证明两条线段平行
1
2
A
B
C
E
D
1、如图,在 ABCD中,AC 与 BD 相交于点 O,点 E 是边 AB 的中点,且 AD=10cm,则 OE 的长是 .
5cm
对应练习
B
C
A
D
O
E
2、如图,D,E, F 分别是 △ABC 三边的中点你能发现△DEF 的面积与 △ABC 的面积有什么关系吗 为什么
●
●
●
A
B
C
D
E
F
原三角形面积的 .
因而每个小三角形的面积为
知识拓展:
三角形的三条中位线
把原三角形
分成了4个全等的小三角形,
1
4
变式:如图,点 D,E,F 分别是 △ABC 各边的中点,若 △ABC 的面积为 20 cm2,则 △DEF的面积 .
A
B
C
F
E
D
5cm2
3、如图,点 D,E,F 分别是 △ABC 各边的中点,若△ABC的周长为 10 cm,求 △DEF 的周长?
对应练习
A
B
C
F
E
D
解:
∵ D,E分别是AB、BC的中点
∴ DE是△ABC的中位线
DE=
BC
1
2
∴
同理可得
DF=
AC,
2
1
EF=
AB
1
2
∴ △DEF的周长为
DE+DF+EF=
BC
1
2
+ AC
1
2
+ AB
1
2
(BC+AC+AB)
1
2
=5(cm)
=
每个小三角形的面积为
每个小三角形的周长为
方法技巧:
三角形的三条中位线
把原三角形
分成了4个全等的小三角形,
原三角形周长的 ,
1
2
原三角形面积的 .
1
4
C
A
B
D
F
E
G
H
I
变式练习:如下图,D、E、F、G、H、I 都是各自所在线段的中点,若 △GHI 的周长是 5 cm,则 △ABC 的周长是 cm.
20
4、已知:如图,在四边形 ABCD 中,E、F、G、H 分别是 AB、BC、CD、DA 的中点. 求证:四边形 EFGH 是平行四边形.
A
B
C
D
E
F
G
H
5、如图四边形 ABCD,点 E、F、G、H 分别是边 AB、BC、CD、DA 的中点,连接 EF、FG、GH、HE,得到四边形 EFGH,求证:四边形 EFGH 是平行四边形.
变式:如图所示,点 O 是 △ABC 内一点,D,E,F,G 分别为 AB,AC,OC,OB 的中点.若 OB⊥OC,OA=6,OC=3,OB=4,求四边形 DEFG 的周长.
76、如图,在四边形 ABCD 中,AD=BC,点 P 是对角线BD 的中点,点 E、F 分别是边 CD 和 AB 的中点,若 ∠PEF=30°,则下列说法错误的是( )
A.PE=PF B.∠EPF=120°
C.AD+BC>2EF D.AB+DC>2DB
7、 如图:如果AD= AC,AE= AB,DE=2cm,
那么BC= cm.
A
B
D
C
E
H
G
8
巩固练习
8、已知:如图,△ABC 是锐角三角形. 分别以 AB,AC 为边向外侧作两个等边△ABM和 △CAN. D,E,F 分别是 MB,BC,CN 的中点,连结 DE,EF. 求证:DE=EF
A
B
C
D
E
F
N
M
9、已知:AD 是 △ABC 的中线,点 E 是AD的中点,点 F 是 BE 延长线与 AC 的交点,求证:AF=FC.
G
本节课你有什么收获?
连接三角形
两边中点
的线段
叫做
三角形的中位线.
① 三角形中位线的定义
三角形两边中点的连线平行于第三边,并且等于等三边的一半
② 三角形中位线定理:
(数量关系)
(位置关系)
主要用途:
(2) 证明一条线段是另一条线段的2倍 或
∵ DE是△ABC的中位线
∴ DE∥ BC,
【几何语言】
(或 AD=BD,AE=CE)
且
DE=
BC
1
2
(1) 证明两条线段平行
1
2
A
B
C
E
D
那么在其他直线上截得的线段也相等.
如果一组平行线
在一条直线上
截得的线段相等,
③ 平行线等分线段定理
l1
l2
l4
A
B
l3
C
l5
A1
B1
C1
平行线等分线段定理推论:
经过三角形一边中点
与另一边平行的直线
必平分第三边.
