沪科版八年级数学下学19.2.1平行四边形边和角的性质 课件(共21张PPT)
文档属性
| 名称 | 沪科版八年级数学下学19.2.1平行四边形边和角的性质 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-17 10:06:01 | ||
图片预览




文档简介
(共21张PPT)
19.2 平行四边形
第19章 四边形
第1课时 平行四边形边和角的性质
情境引入
问题:观察下图中的竹篱笆格子和汽车的防护链,想一想它们是
什么几何图形的形象?
平行四边形
1.理解平行四边形的有关概念;
2.能根据定义掌握平行四边形的对边相等、对角相等的性质.(重点、难点)
学习目标
自主学习
自主梳理课本P75-P76的知识点:
自主梳理例1的解题思路,理解平行四边形的边、角性质.
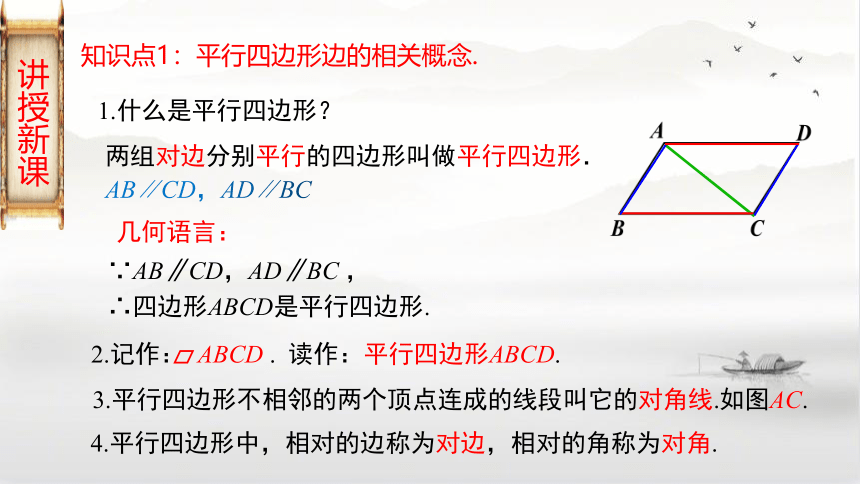
1.什么是平行四边形?
2.记作: ABCD . 读作:平行四边形ABCD.
∵AB∥CD,AD∥BC ,
∴四边形ABCD是平行四边形.
3.平行四边形不相邻的两个顶点连成的线段叫它的对角线.如图AC.
4.平行四边形中,相对的边称为对边,相对的角称为对角.
讲授新课
知识点1:平行四边形边的相关概念.
两组对边分别平行的四边形叫做平行四边形.
AB∥CD,AD∥BC
几何语言:
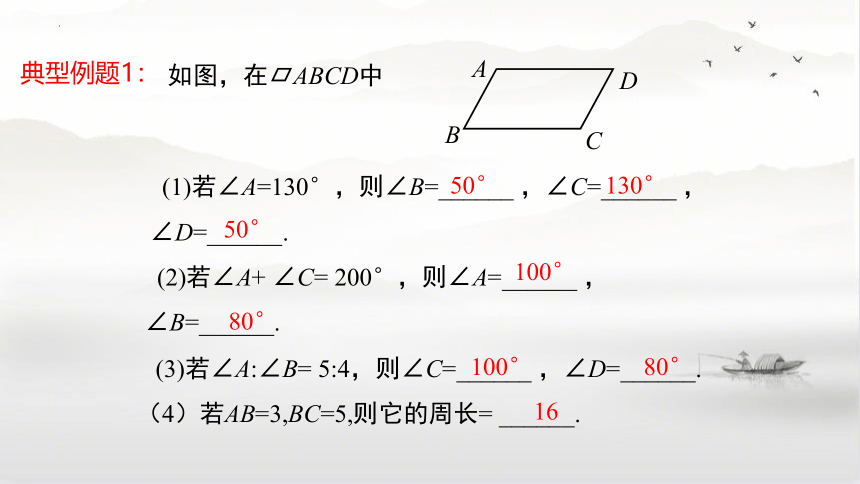
(1)若∠A=130°,则∠B=______ ,∠C=______ , ∠D=______.
(2)若∠A+ ∠C= 200°,则∠A=______ ,∠B=______.
(3)若∠A:∠B= 5:4,则∠C=______ ,∠D=______.
(4)若AB=3,BC=5,则它的周长= ______.
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
16
如图,在 ABCD中
典型例题1:
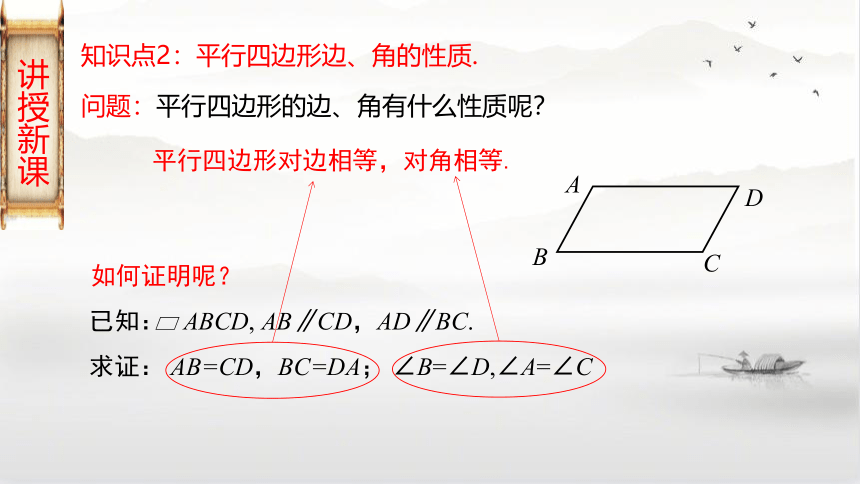
问题:平行四边形的边、角有什么性质呢?
一
讲授新课
知识点2:平行四边形边、角的性质.
平行四边形对边相等,对角相等.
已知: ABCD, AB∥CD,AD∥BC.
求证: AB=CD,BC=DA; ∠B=∠D,∠A=∠C
如何证明呢?
C
D
A
B
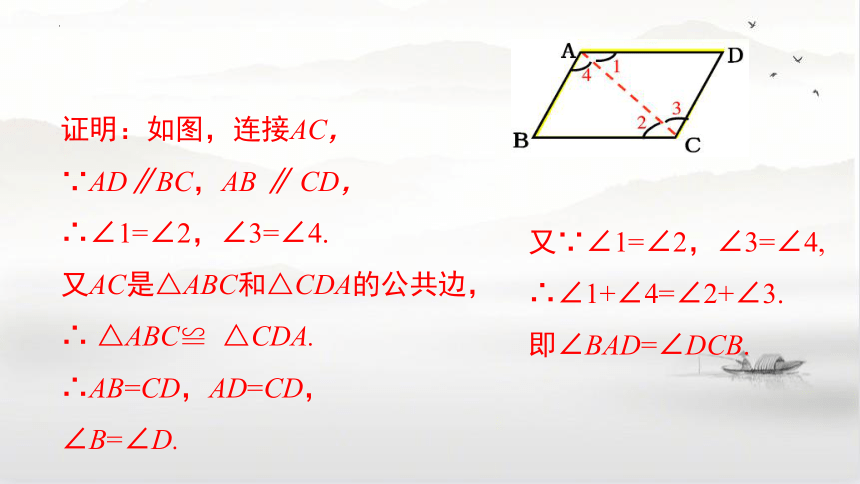
证明:如图,连接AC,
∵AD∥BC,AB ∥ CD,
∴∠1=∠2,∠3=∠4.
又AC是△ABC和△CDA的公共边,
∴ △ABC≌ △CDA.
∴AB=CD,AD=CD,
∠B=∠D.
又∵∠1=∠2,∠3=∠4,
∴∠1+∠4=∠2+∠3.
即∠BAD=∠DCB.
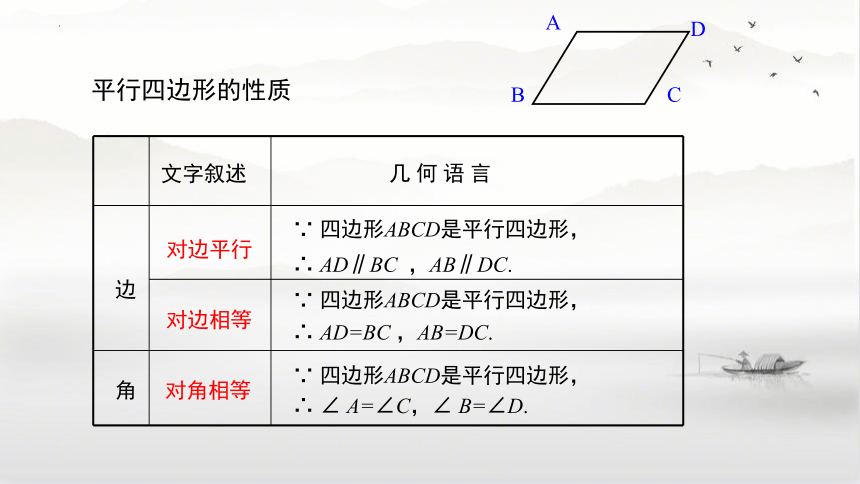
几 何 语 言
边
角
文字叙述
对边平行
对边相等
对角相等
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠ A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
A
B
C
D
平行四边形的性质
解:在 ABCD中,AB=DC, AD=BC,
(平行四边形的对边相等)
∵ AB=8,DC=8,
又∵AB+BC+DC+AD=24,
∴AD+BC= (24-2AB)=8.
∴AD=BC=4.
B
C
D
A
如图,在 ABCD中,AB=8,周长等于24,求其余三条边的长.
典型例题2:
如图,// , 上A、B、C三点,过A、B、C三点作的垂线段
AD、BE、CF,AD=BE=CF吗?
那么AD、BE、CF为平行线之间的距离且平行线间距离处处相等.
讲授新课
知识点3:平行线之间的距离.
A
B
C
D
E
F
1
证明:如图,直线a//b,A,B是直线a上任意两点,AC⊥b,BD⊥b,垂足分别为C,D.求证:AC=BD.
证明:∵AC⊥CD,BD⊥CD,
a
b
A
B
C
D
∴∠1=∠2=90°.
∴AC∥BD.
∵AB∥CD,
∴四边形ACDB是平行四边形.
∴AC=BD.
2
归纳:
如果两条直线互相平行,则其中一条直线上任意一点到另一条直线的距离都相等(如图:AC=BD),这个距离称为平行线之间的距离.
(简记为:两条平行线间的距离处处相等).
思考:若夹在两条线段间的是平行线段呢?它们是否还相等呢?
即夹在两条平行线间的平行线段相等.
A
B
C
D
如图,直线AE//BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为 .
A
B
C
D
E
解析:设高为h,则S△ABD= ·BD·h=16,h=4,
所以S △ACE= ×5 ×4=10.
10
典型例题3:
课堂训练
1.
2.
课堂训练
课堂训练
3.
证明:∵四边形ABCD是平行四边形,
∴∠BAE=∠DCF.
∴ △ABE≌ △CDF.
∴ AB=CD,AD ∥ BC,
又∵AE=CF,
∴BE=DF.
A
D
B
C
E
F
4. 已知: ABCD, E,F是对角线AC上的两点,并且AE=CF,求证: BE=DF.
课堂训练
课堂训练
5.
平行四边形
两组对边分别平行的四边形是平行四边形
定义:
性质:
对边平行,
对边相等,
对角相等
夹在两条平行线间的平行线段处处相等
课堂小结
作业布置
课本P84,习题第1题、第2题.
19.2 平行四边形
第19章 四边形
第1课时 平行四边形边和角的性质
情境引入
问题:观察下图中的竹篱笆格子和汽车的防护链,想一想它们是
什么几何图形的形象?
平行四边形
1.理解平行四边形的有关概念;
2.能根据定义掌握平行四边形的对边相等、对角相等的性质.(重点、难点)
学习目标
自主学习
自主梳理课本P75-P76的知识点:
自主梳理例1的解题思路,理解平行四边形的边、角性质.
1.什么是平行四边形?
2.记作: ABCD . 读作:平行四边形ABCD.
∵AB∥CD,AD∥BC ,
∴四边形ABCD是平行四边形.
3.平行四边形不相邻的两个顶点连成的线段叫它的对角线.如图AC.
4.平行四边形中,相对的边称为对边,相对的角称为对角.
讲授新课
知识点1:平行四边形边的相关概念.
两组对边分别平行的四边形叫做平行四边形.
AB∥CD,AD∥BC
几何语言:
(1)若∠A=130°,则∠B=______ ,∠C=______ , ∠D=______.
(2)若∠A+ ∠C= 200°,则∠A=______ ,∠B=______.
(3)若∠A:∠B= 5:4,则∠C=______ ,∠D=______.
(4)若AB=3,BC=5,则它的周长= ______.
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
16
如图,在 ABCD中
典型例题1:
问题:平行四边形的边、角有什么性质呢?
一
讲授新课
知识点2:平行四边形边、角的性质.
平行四边形对边相等,对角相等.
已知: ABCD, AB∥CD,AD∥BC.
求证: AB=CD,BC=DA; ∠B=∠D,∠A=∠C
如何证明呢?
C
D
A
B
证明:如图,连接AC,
∵AD∥BC,AB ∥ CD,
∴∠1=∠2,∠3=∠4.
又AC是△ABC和△CDA的公共边,
∴ △ABC≌ △CDA.
∴AB=CD,AD=CD,
∠B=∠D.
又∵∠1=∠2,∠3=∠4,
∴∠1+∠4=∠2+∠3.
即∠BAD=∠DCB.
几 何 语 言
边
角
文字叙述
对边平行
对边相等
对角相等
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠ A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
A
B
C
D
平行四边形的性质
解:在 ABCD中,AB=DC, AD=BC,
(平行四边形的对边相等)
∵ AB=8,DC=8,
又∵AB+BC+DC+AD=24,
∴AD+BC= (24-2AB)=8.
∴AD=BC=4.
B
C
D
A
如图,在 ABCD中,AB=8,周长等于24,求其余三条边的长.
典型例题2:
如图,// , 上A、B、C三点,过A、B、C三点作的垂线段
AD、BE、CF,AD=BE=CF吗?
那么AD、BE、CF为平行线之间的距离且平行线间距离处处相等.
讲授新课
知识点3:平行线之间的距离.
A
B
C
D
E
F
1
证明:如图,直线a//b,A,B是直线a上任意两点,AC⊥b,BD⊥b,垂足分别为C,D.求证:AC=BD.
证明:∵AC⊥CD,BD⊥CD,
a
b
A
B
C
D
∴∠1=∠2=90°.
∴AC∥BD.
∵AB∥CD,
∴四边形ACDB是平行四边形.
∴AC=BD.
2
归纳:
如果两条直线互相平行,则其中一条直线上任意一点到另一条直线的距离都相等(如图:AC=BD),这个距离称为平行线之间的距离.
(简记为:两条平行线间的距离处处相等).
思考:若夹在两条线段间的是平行线段呢?它们是否还相等呢?
即夹在两条平行线间的平行线段相等.
A
B
C
D
如图,直线AE//BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为 .
A
B
C
D
E
解析:设高为h,则S△ABD= ·BD·h=16,h=4,
所以S △ACE= ×5 ×4=10.
10
典型例题3:
课堂训练
1.
2.
课堂训练
课堂训练
3.
证明:∵四边形ABCD是平行四边形,
∴∠BAE=∠DCF.
∴ △ABE≌ △CDF.
∴ AB=CD,AD ∥ BC,
又∵AE=CF,
∴BE=DF.
A
D
B
C
E
F
4. 已知: ABCD, E,F是对角线AC上的两点,并且AE=CF,求证: BE=DF.
课堂训练
课堂训练
5.
平行四边形
两组对边分别平行的四边形是平行四边形
定义:
性质:
对边平行,
对边相等,
对角相等
夹在两条平行线间的平行线段处处相等
课堂小结
作业布置
课本P84,习题第1题、第2题.
