沪科版2021-2022学年八年级数学下册19.3.1矩形的性质和推论 同步精品课件 (共41张PPT)
文档属性
| 名称 | 沪科版2021-2022学年八年级数学下册19.3.1矩形的性质和推论 同步精品课件 (共41张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 647.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-17 00:00:00 | ||
图片预览



文档简介
(共41张PPT)
知识回顾
A
B
D
C
O
平行四边形的对边平行
平行四边形的对角相等,
且相等.
邻角互补.
平行四边形的
对角线
互相平分
对角线的性质
平行四边形有哪些性质?
边的性质
角的性质
从边来判定
平行四边形的判定方法
知识回顾
从角来判定
从对角线来判定
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
(平行四边形的定义)
(判定定理1)
两组对边分别相等的四边形是平行四边形
(判定定理2)
两组对角分别相等的四边形是平行四边形
(本教材没有给出)
对角线互相平分的四边形是平行四边形
(判定定理3)
连接三角形
两边中点
的线段
叫做
三角形的中位线.
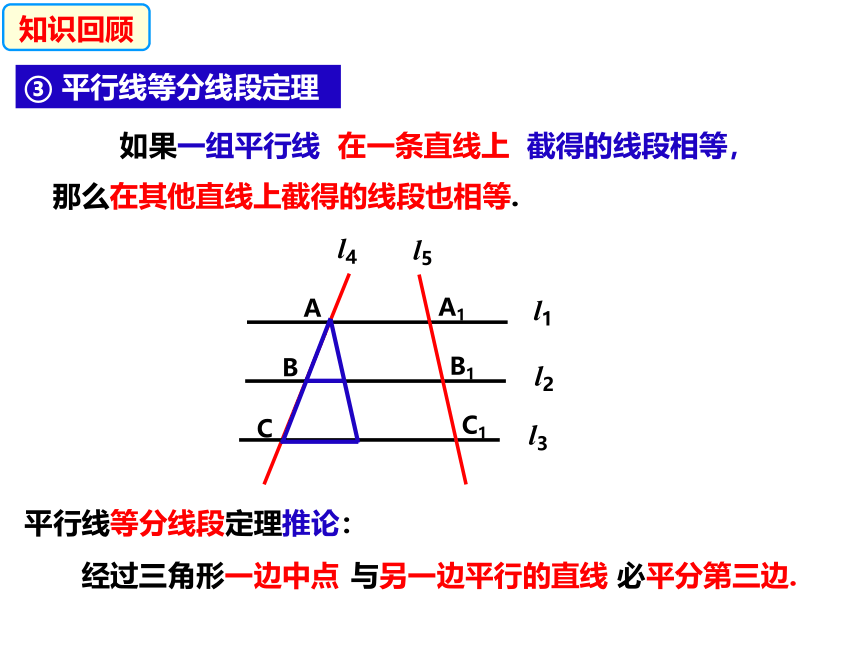
① 三角形中位线的定义
三角形两边中点的连线平行于第三边,并且等于等三边的一半
② 三角形中位线定理:
(数量关系)
(位置关系)
主要用途:
(2) 证明一条线段是另一条线段的2倍 或
∵ DE是△ABC的中位线
∴ DE∥ BC,
【几何语言】
(或 AD=BD,AE=CE)
且
DE=
BC
1
2
(1) 证明两条线段平行
1
2
A
B
C
E
D
知识回顾
那么在其他直线上截得的线段也相等.
如果一组平行线
在一条直线上
截得的线段相等,
③ 平行线等分线段定理
l1
l2
l4
A
B
l3
C
l5
A1
B1
C1
平行线等分线段定理推论:
经过三角形一边中点
与另一边平行的直线
必平分第三边.
知识回顾
19.3.1 矩形及其性质
创设情境
电脑、电视机的显示屏是什么形状?本书的封面是什么形状?
小学阶段我们称这些图形为长方形
也叫做矩形
思考:矩形跟我们前面学行四边形有什么关系?
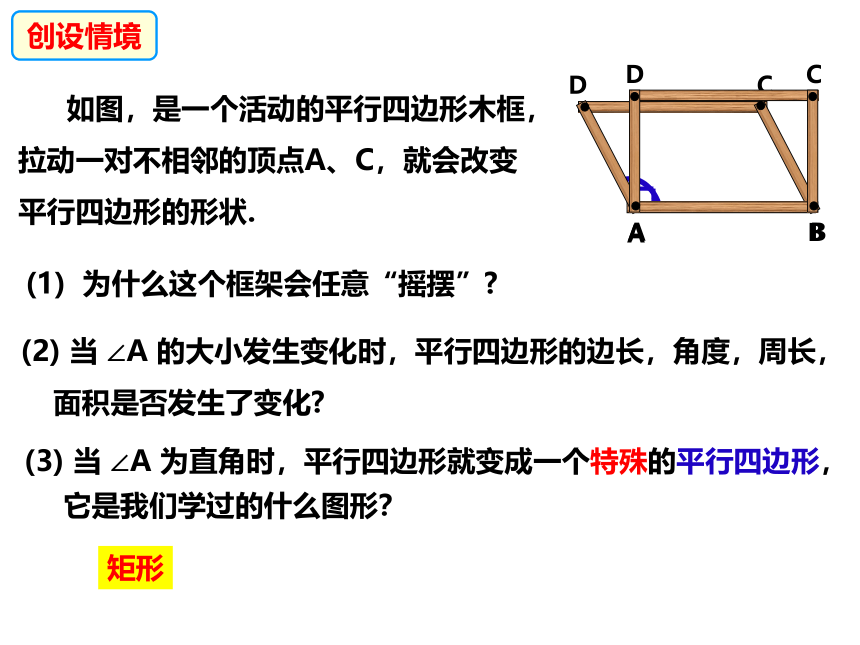
如图,是一个活动的平行四边形木框,拉动一对不相邻的顶点A、C,就会改变平行四边形的形状.
A
B
C
D
创设情境
(2) 当 ∠A 的大小发生变化时,平行四边形的边长,角度,周长,面积是否发生了变化
(3) 当 ∠A 为直角时,平行四边形就变成一个特殊的平行四边形,
它是我们学过的什么图形?
A
B
C
D
矩形
(1) 为什么这个框架会任意“摇摆”
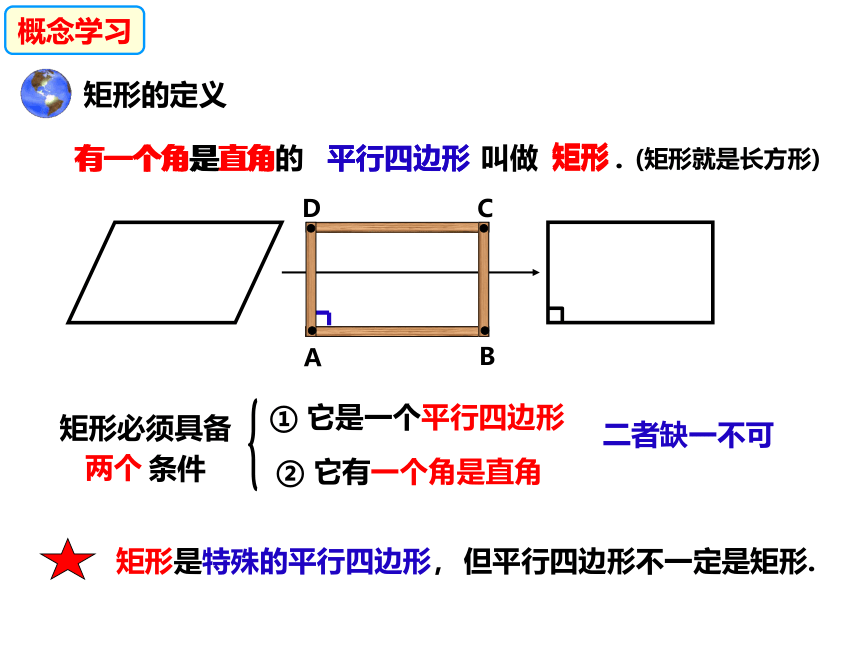
有一个角是直角的
叫做 .
矩形
平行四边形
矩形
有一个角是直角
平行四边形
矩形的定义
概念学习
A
B
C
D
矩形必须具备
两个
① 它是一个平行四边形
② 它有一个角是直角
条件
二者缺一不可
矩形是特殊的平行四边形,
但平行四边形不一定是矩形.
(矩形就是长方形)
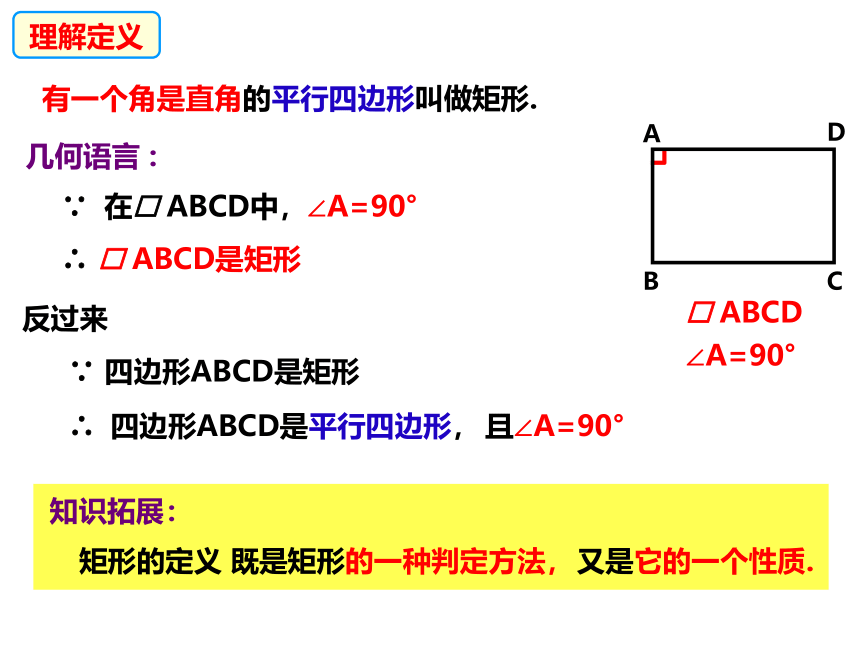
有一个角是直角的平行四边形叫做矩形.
理解定义
几何语言 :
∵ 在 ABCD中,
∴ ABCD是矩形
反过来
∴ 四边形ABCD是平行四边形,
∵ 四边形ABCD是矩形
知识拓展:
∠A=90°
且∠A=90°
ABCD
∠A=90°
又是它的一个性质.
矩形的定义
既是矩形的一种判定方法,
A
B
D
C
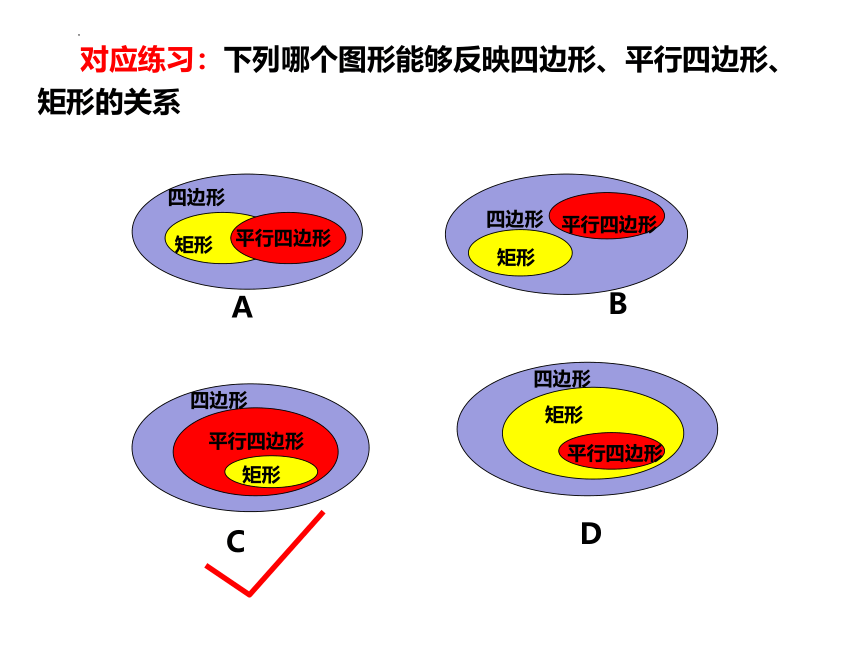
对应练习:下列哪个图形能够反映四边形、平行四边形、
矩形的关系
D
C
四边形
矩形
平行四边形
四边形
矩形
平行四边形
四边形
矩形
平行四边形
平行四边形
矩形
四边形
A
B
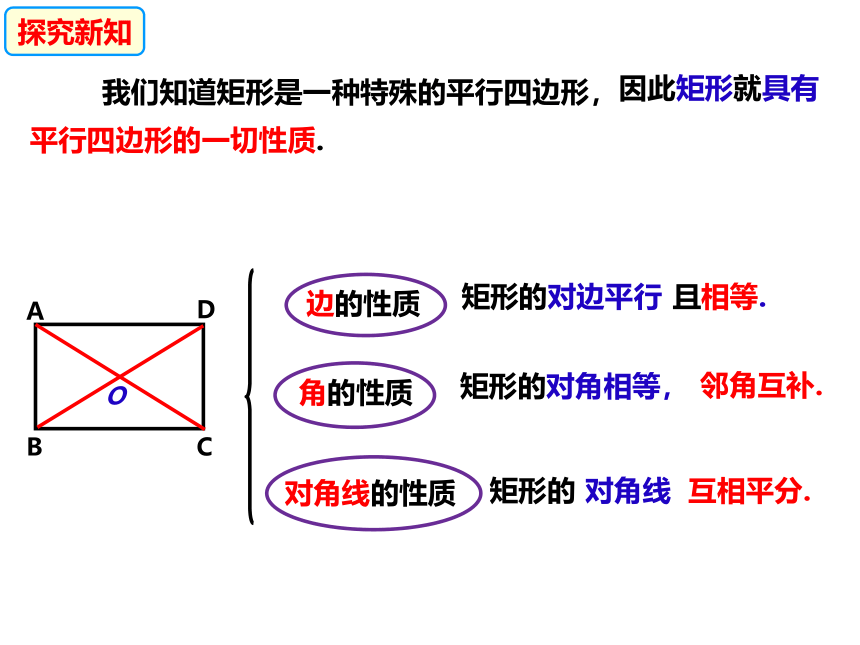
因此矩形就具有平行四边形的一切性质.
探究新知
我们知道矩形是一种特殊的平行四边形,
A
B
D
C
对角线的性质
边的性质
角的性质
矩形的对边平行
矩形的对角相等,
且相等.
邻角互补.
O
矩形的
对角线
互相平分.
探究新知
A
B
D
C
O
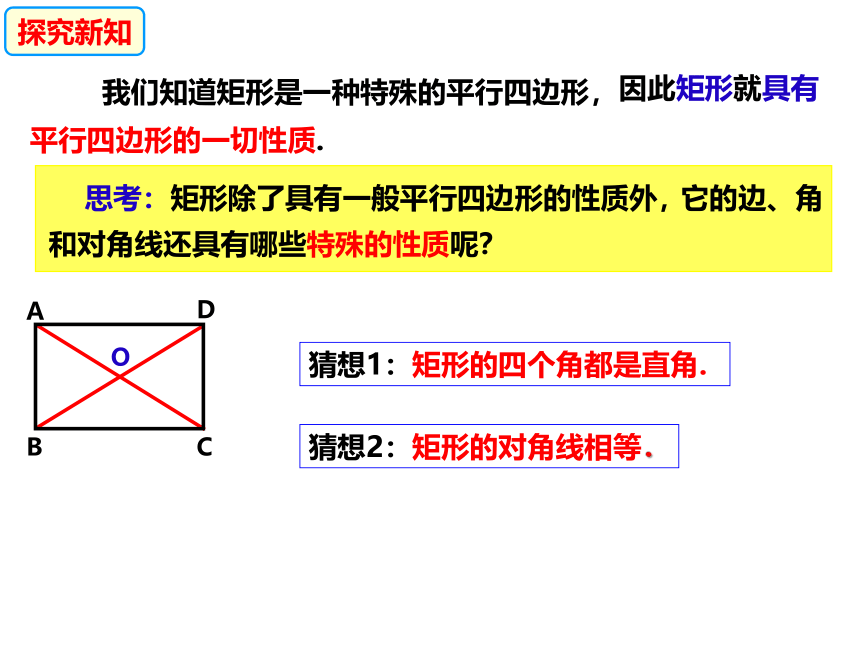
它的边、角和对角线还具有哪些特殊的性质呢?
思考:矩形除了具有一般平行四边形的性质外,
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
因此矩形就具有平行四边形的一切性质.
我们知道矩形是一种特殊的平行四边形,
已知:
求证:
证明:
∵ 四边形 ABCD 是矩形
∴ ∠A=∠C=90°,
矩形的四个角都是直角.
猜想 1:
A
B
D
C
∠A=∠B=∠C=∠D=90°
如图,四边形 ABCD 是矩形.
由定义,
矩形必有一个角是直角,
设∠A=90°
∠B=∠D,
AD∥BC
∴ ∠B=180°-90°=90°
∴ ∠A=∠B=∠C=∠D=90°
即 矩形 ABCD 的四个角都是直角.
A
B
D
C
已知:
猜想2:矩形的对角线相等.
O
求证:AC = BD
在矩形ABCD中,对角线AC和BD相交于点O.
∵ 四边形ABCD是矩形
∴ △ABC≌△DCB
∴ AC=BD
∠ABC = ∠DCB = 90°
(矩形的对边相等)
(矩形的四个角都是直角)
在△ABC和△DCB中
AB=DC
∠ABC=∠DCB
BC=CB
证明:
∴ AB = DC
∵
(公共边)
(SAS)
矩形特殊的性质
矩形的四个角都是直角.
矩形的两条对角线相等.
性质 1:
性质 2:
A
B
D
C
O
∵ 四边形ABCD是矩形
∴ ∠ABC=∠BCD=∠CDA=∠DAB=90°
【几何语言】
(矩形的四个角都是直角)
∵ 四边形ABCD是矩形
∴ AC=BD
【几何语言】
(矩形的两条对角线相等)
∵ 四边形ABCD是矩形
∴ AC=BD,
矩
形
的
性
质
A
B
D
C
O
矩形的对边平行
矩形的四个角都是直角
且相等.
矩形的
对角线
相等
对角线的性质
边的性质
角的性质
归纳总结
且互相平分
∵ 四边形ABCD是矩形
∴ AB CD,
BC AD
∵ 四边形ABCD是矩形
∴ ∠ABC=∠BCD=∠CDA=∠DAB=90°
且 OA
=OB
=OC
=OD
对边平行
且相等
对角相等
邻角互补
对角线
互相平分
对边平行
且相等
四个角
为直角
对角线相等且互相平分
这是矩形所特有的性质……
比一比
边
角
对角线
平行四
边形
矩形
A
B
D
C
O
1、矩形具有而一般平行四边形不具有的性质是 ( )
A.对角相等 B.对边相等
C.对角线相等 D.对角线互相平分
C
对应练习
2、如图,矩形 ABCD 的对角线 AC、BD 相交于点 O,图中有多少个直角三角形?有多少个等腰三角形?
探究新知
A
B
D
C
O
直角三角形:
4个
Rt△ADC
Rt△ABC
Rt△BCD
Rt△BAD
等腰三角形:
4个
△COD
△AOB
△BOC
△AOD
矩形的两条对角线
知识拓展:
矩形的
每条对角线
把矩形分成两个直角三角形,
将矩形分成四个等腰三角形.
矩形问题
直角三角形和等腰三角形中来解决
转化
3、如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD面积的_________.
4
1
G
知识拓展:
S△AOB=
S△BOC=
S△COD=
S矩形ABCD
S△AOD
D
A
C
B
O
4、已知:如图,矩形 ABCD 的两条对角线相交于点 O,∠AOB=120°,AD=4cm. 求矩形对角线的长.
解:
∵ 四边形ABCD是矩形
∴ AC=BD,
OA=OB
又∵ ∠AOB=120°
∴ ∠OAB=
∠OBA
=
2
180°-120°
=30°
∵ 在Rt△ABD中,∠OBA=30°,AD=4cm.
∴ AC=BD=
2AD
=8 (cm)
5、已知矩形的一条对角线长8cm,两条对角线的夹角为60°,矩形相邻两边的长各为多少?
A
B
D
C
O
6、如图,在矩形 ABCD 中,∠BAD 的平分线交 BC 于点 E,O 为对角线 AC、BD 的交点,且 ∠CAE=15°
(1) 求证:△AOB 为等边三角形;
(2) 求 ∠AOE 度数.
如图,一张矩形纸片,画出两条对角线,沿着对角线 AC 剪去一半.
探究新知
A
B
D
C
O
A
B
C
O
问题:在 Rt△ABC 中, BO 是一条怎样的线段?它的长度与斜边 AC 有什么关系?
2
1
OB=
OA
猜想:
直角三角形斜边上的中线等于斜边的一半.
你能证明吗?
OB = AC .
连接AD、DC.
∴ 四边形ABCD是平行四边形
∵ ∠ABC=90°
∴ 平行四边形ABCD是矩形
∴ AC=BD
已知:
∴ OB=
验证结论
A
B
C
O
D
求证:
在Rt△ABC中,
如图,
∠ABC=90°,
OB是AC上的中线.
2
1
证明:
延长BO至D,
使OD=OB,
∵ OA=OC, OD=OB
BD
= AC
2
1
2
1
猜想:
直角三角形斜边上的中线等于斜边的一半.
归纳小结
A
B
C
O
直角三角形斜边上的中线定理:
∵ 在Rt△ABC中,
【几何语言】
= AC
2
1
∴ OB
(或 OB=OA=OC, )
点O是斜边AC的中点
或 AC=2OB
直角三角形斜边上的中线等于斜边的一半.
7、如图,在△ABC中,∠ABC = 90°,BD 是斜边 AC 上的中线.
(1) 若 BD=3cm,则AC =_____cm;
(2) 若∠C = 30°,AB =5cm,则AC =_____cm, BD = _____cm.
(3) 若∠C=35°,则 ∠ABD= .
A
B
C
D
6
10
5
巩固练习
55°
8、如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则EF=______cm.
2.5
巩固练习
9、如图,DE 为 △ABC 的中位线,点 F 在 DE 上,且∠AFB=90°,若 AB=5,BC=8,则 EF 的长为 .
1
巩固练习
10、如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.
(1)若AB=10,AC=8,求四边形AEDF的周长;
解:
∵ 在Rt△ADB中,
∵ AD是△ABC的高
∴ DE=
AE
= AB
= ×10
2
1
2
1
∴ ∠ADB=∠ADC=90°
且AB=10
又∵ 在Rt△ADC中,
∴ DF=
AF
= AC
= ×8
2
1
2
1
且AC=8
=5
=4
AE+DE+DF+AF
∴ 四边形AEDF的周长为
点E为斜边AB的中点,
点F为斜边AC的中点,
=5+5+4+4
=18
方法技巧:
可联想直角三角形斜边上的中线的性质进行求解.
当已知条件含有线段的中点、
直角三角形的条件时,
(2) 求证:EF垂直平分AD.
由(1)可得
证明:
∴ E、F在线段AD的垂直平分线上
∴ EF垂直平分AD
DE=AE,DF=AF
(与线段两端距离相等的点在这条线段的垂直平分线上)
10、如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.
(1)若AB=10,AC=8,求四边形AEDF的周长;
11、 如图,已知BD,CE是△ABC不同边上的高,点G,F分别是BC,DE的中点,试说明 GF⊥DE.
解:
∵ 在Rt△BEC 中,
∵ BD,CE 分别为△ABC边上的高
∴ EG=
BC
2
1
∴ ∠BEC=∠BDC=90°
又∵ 在Rt△BDC中,
点G为斜边BC的中点
点G为斜边BC的中点
∴ DG=
BC
2
1
∴ EG=DG
又∵ F为DE的中点
∴ GF⊥DE
连接EG,DG
方法技巧:
可联想直角三角形斜边上的中线的性质进行求解.
当已知条件含有线段的中点、
直角三角形的条件时,
12、如图,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,求PE+PF的值.
A
B
D
C
P
O
E
F
解:
连接OP
∵ 四边形ABCD是矩形
∴ ∠DAB=90°,
OA=OB=OC=OD
∴ S△AOD=S△DOC=S△AOB=S△BOC
4
1
= S矩形ABCD
4
1
= ×6×8=12
∵ 在Rt△ABD中,AB=6,AD=8
∴ BD=
=10
∴ PE+PF=
又∵ S△APO+S△DPO=S△AOD
2
1
2
1
+ ×OD×PF
=12
即
2
1
×5×PE
2
1
+ ×5×PF
=12
∴ OA=OD=5
5
24
∴ ×OA×PE
H
13、如图,将矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=4,求△BED的面积.
解:∵ 四边形ABCD是矩形
∴ AD∥ BC,
∴ ∠2=∠3
由折叠知 ∠1=∠2
∴ ∠1=∠3
∴ BE=DE
设BE=DE=x,
∵ 在Rt△ABE中,AB2+AE2=BE2
∴ 42+(8-x)2=x2,
解得 x=5
∴ S△BED=
矩形的折叠问题常与勾股定理结合考查
∠A=90°
则AE=8-x
即 DE=5
=10
= ×5×4
DE·AB
2
1
2
1
14、如图,点 P 是矩形 ABCD 的对角线 AC 上一点,过点 P 作EF∥BC,分别交 AB,CD 于 E、F,连接 PB、PD.若 AE=2,PF=8.则图中阴影部分的面积为( )
A.10 B.12 C.16 D.18
M
N
15、如图,在矩形ABCD中,点M在DC上,AM=AB,且BN⊥AM,垂足为N.
(1) 求证:△ABN≌△MAD;
(2) 若AD=2,AN=4,求四边形BCMN的面积.
BC=BN
16、如图,在矩形 ABCD 中,AE⊥BD 于 E,∠DAE:∠BAE=3:1,求 ∠BAO 和 ∠EAO 的度数.
A
B
D
C
O
E
∴ ∠DAE=67.5°,
∠BAE=22.5°
∵ AE⊥BD
∴ ∠ABE=
90°-∠BAE
=67.5°
∵ OA=OB
∴ ∠BAO=
∠ABE
=67.5°
∴ ∠EAO=
∠BAO-∠BAE
=67.5°-22.5°
=45°
矩形的两条对角线
知识拓展:
矩形的
每条对角线
把矩形分成两个直角三角形,
将矩形分成四个等腰三角形.
矩形问题
直角三角形和等腰三角形中来解决
转化
本节课你有什么收获?
有一个角是直角的平行四边形叫做矩形.
理解定义
几何语言 :
∵ 在 ABCD中,
∴ ABCD是矩形
反过来
∴ 四边形ABCD是平行四边形,
∵ 四边形ABCD是矩形
注意:
∠A=90°
且∠A=90°
ABCD
∠A=90°
又是它的一个性质.
矩形的定义
既是矩形的一种判定方法,
A
B
D
C
∵ 四边形ABCD是矩形
∴ AC=BD,
矩
形
的
性
质
A
B
D
C
O
矩形的对边平行
矩形的四个角都是直角
且相等.
矩形的
对角线
相等
对角线的性质
边的性质
角的性质
归纳总结
且互相平分
∵ 四边形ABCD是矩形
∴ AB CD,
BC AD
∵ 四边形ABCD是矩形
∴ ∠ABC=∠BCD=∠CDA=∠DAB=90°
且 OA
=OB
=OC
=OD
矩形的两条对角线
知识拓展:
矩形的
每条对角线
把矩形分成两个直角三角形,
将矩形分成四个等腰三角形.
矩形问题
直角三角形和等腰三角形中来解决
转化
归纳小结
A
B
C
O
直角三角形
斜边上的中线
等于
斜边的一半.
直角三角形斜边上的中线定理:
∵ 在Rt△ABC中,,
【几何语言】
= AC
2
1
∴ OB
(或 OB=OA=OC, )
点O是斜边AC的中点
或 AC=2OB
方法技巧:
可联想直角三角形斜边上的中线的性质进行求解.
当已知条件含有线段的中点、
直角三角形的条件时,
知识回顾
A
B
D
C
O
平行四边形的对边平行
平行四边形的对角相等,
且相等.
邻角互补.
平行四边形的
对角线
互相平分
对角线的性质
平行四边形有哪些性质?
边的性质
角的性质
从边来判定
平行四边形的判定方法
知识回顾
从角来判定
从对角线来判定
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
(平行四边形的定义)
(判定定理1)
两组对边分别相等的四边形是平行四边形
(判定定理2)
两组对角分别相等的四边形是平行四边形
(本教材没有给出)
对角线互相平分的四边形是平行四边形
(判定定理3)
连接三角形
两边中点
的线段
叫做
三角形的中位线.
① 三角形中位线的定义
三角形两边中点的连线平行于第三边,并且等于等三边的一半
② 三角形中位线定理:
(数量关系)
(位置关系)
主要用途:
(2) 证明一条线段是另一条线段的2倍 或
∵ DE是△ABC的中位线
∴ DE∥ BC,
【几何语言】
(或 AD=BD,AE=CE)
且
DE=
BC
1
2
(1) 证明两条线段平行
1
2
A
B
C
E
D
知识回顾
那么在其他直线上截得的线段也相等.
如果一组平行线
在一条直线上
截得的线段相等,
③ 平行线等分线段定理
l1
l2
l4
A
B
l3
C
l5
A1
B1
C1
平行线等分线段定理推论:
经过三角形一边中点
与另一边平行的直线
必平分第三边.
知识回顾
19.3.1 矩形及其性质
创设情境
电脑、电视机的显示屏是什么形状?本书的封面是什么形状?
小学阶段我们称这些图形为长方形
也叫做矩形
思考:矩形跟我们前面学行四边形有什么关系?
如图,是一个活动的平行四边形木框,拉动一对不相邻的顶点A、C,就会改变平行四边形的形状.
A
B
C
D
创设情境
(2) 当 ∠A 的大小发生变化时,平行四边形的边长,角度,周长,面积是否发生了变化
(3) 当 ∠A 为直角时,平行四边形就变成一个特殊的平行四边形,
它是我们学过的什么图形?
A
B
C
D
矩形
(1) 为什么这个框架会任意“摇摆”
有一个角是直角的
叫做 .
矩形
平行四边形
矩形
有一个角是直角
平行四边形
矩形的定义
概念学习
A
B
C
D
矩形必须具备
两个
① 它是一个平行四边形
② 它有一个角是直角
条件
二者缺一不可
矩形是特殊的平行四边形,
但平行四边形不一定是矩形.
(矩形就是长方形)
有一个角是直角的平行四边形叫做矩形.
理解定义
几何语言 :
∵ 在 ABCD中,
∴ ABCD是矩形
反过来
∴ 四边形ABCD是平行四边形,
∵ 四边形ABCD是矩形
知识拓展:
∠A=90°
且∠A=90°
ABCD
∠A=90°
又是它的一个性质.
矩形的定义
既是矩形的一种判定方法,
A
B
D
C
对应练习:下列哪个图形能够反映四边形、平行四边形、
矩形的关系
D
C
四边形
矩形
平行四边形
四边形
矩形
平行四边形
四边形
矩形
平行四边形
平行四边形
矩形
四边形
A
B
因此矩形就具有平行四边形的一切性质.
探究新知
我们知道矩形是一种特殊的平行四边形,
A
B
D
C
对角线的性质
边的性质
角的性质
矩形的对边平行
矩形的对角相等,
且相等.
邻角互补.
O
矩形的
对角线
互相平分.
探究新知
A
B
D
C
O
它的边、角和对角线还具有哪些特殊的性质呢?
思考:矩形除了具有一般平行四边形的性质外,
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
因此矩形就具有平行四边形的一切性质.
我们知道矩形是一种特殊的平行四边形,
已知:
求证:
证明:
∵ 四边形 ABCD 是矩形
∴ ∠A=∠C=90°,
矩形的四个角都是直角.
猜想 1:
A
B
D
C
∠A=∠B=∠C=∠D=90°
如图,四边形 ABCD 是矩形.
由定义,
矩形必有一个角是直角,
设∠A=90°
∠B=∠D,
AD∥BC
∴ ∠B=180°-90°=90°
∴ ∠A=∠B=∠C=∠D=90°
即 矩形 ABCD 的四个角都是直角.
A
B
D
C
已知:
猜想2:矩形的对角线相等.
O
求证:AC = BD
在矩形ABCD中,对角线AC和BD相交于点O.
∵ 四边形ABCD是矩形
∴ △ABC≌△DCB
∴ AC=BD
∠ABC = ∠DCB = 90°
(矩形的对边相等)
(矩形的四个角都是直角)
在△ABC和△DCB中
AB=DC
∠ABC=∠DCB
BC=CB
证明:
∴ AB = DC
∵
(公共边)
(SAS)
矩形特殊的性质
矩形的四个角都是直角.
矩形的两条对角线相等.
性质 1:
性质 2:
A
B
D
C
O
∵ 四边形ABCD是矩形
∴ ∠ABC=∠BCD=∠CDA=∠DAB=90°
【几何语言】
(矩形的四个角都是直角)
∵ 四边形ABCD是矩形
∴ AC=BD
【几何语言】
(矩形的两条对角线相等)
∵ 四边形ABCD是矩形
∴ AC=BD,
矩
形
的
性
质
A
B
D
C
O
矩形的对边平行
矩形的四个角都是直角
且相等.
矩形的
对角线
相等
对角线的性质
边的性质
角的性质
归纳总结
且互相平分
∵ 四边形ABCD是矩形
∴ AB CD,
BC AD
∵ 四边形ABCD是矩形
∴ ∠ABC=∠BCD=∠CDA=∠DAB=90°
且 OA
=OB
=OC
=OD
对边平行
且相等
对角相等
邻角互补
对角线
互相平分
对边平行
且相等
四个角
为直角
对角线相等且互相平分
这是矩形所特有的性质……
比一比
边
角
对角线
平行四
边形
矩形
A
B
D
C
O
1、矩形具有而一般平行四边形不具有的性质是 ( )
A.对角相等 B.对边相等
C.对角线相等 D.对角线互相平分
C
对应练习
2、如图,矩形 ABCD 的对角线 AC、BD 相交于点 O,图中有多少个直角三角形?有多少个等腰三角形?
探究新知
A
B
D
C
O
直角三角形:
4个
Rt△ADC
Rt△ABC
Rt△BCD
Rt△BAD
等腰三角形:
4个
△COD
△AOB
△BOC
△AOD
矩形的两条对角线
知识拓展:
矩形的
每条对角线
把矩形分成两个直角三角形,
将矩形分成四个等腰三角形.
矩形问题
直角三角形和等腰三角形中来解决
转化
3、如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD面积的_________.
4
1
G
知识拓展:
S△AOB=
S△BOC=
S△COD=
S矩形ABCD
S△AOD
D
A
C
B
O
4、已知:如图,矩形 ABCD 的两条对角线相交于点 O,∠AOB=120°,AD=4cm. 求矩形对角线的长.
解:
∵ 四边形ABCD是矩形
∴ AC=BD,
OA=OB
又∵ ∠AOB=120°
∴ ∠OAB=
∠OBA
=
2
180°-120°
=30°
∵ 在Rt△ABD中,∠OBA=30°,AD=4cm.
∴ AC=BD=
2AD
=8 (cm)
5、已知矩形的一条对角线长8cm,两条对角线的夹角为60°,矩形相邻两边的长各为多少?
A
B
D
C
O
6、如图,在矩形 ABCD 中,∠BAD 的平分线交 BC 于点 E,O 为对角线 AC、BD 的交点,且 ∠CAE=15°
(1) 求证:△AOB 为等边三角形;
(2) 求 ∠AOE 度数.
如图,一张矩形纸片,画出两条对角线,沿着对角线 AC 剪去一半.
探究新知
A
B
D
C
O
A
B
C
O
问题:在 Rt△ABC 中, BO 是一条怎样的线段?它的长度与斜边 AC 有什么关系?
2
1
OB=
OA
猜想:
直角三角形斜边上的中线等于斜边的一半.
你能证明吗?
OB = AC .
连接AD、DC.
∴ 四边形ABCD是平行四边形
∵ ∠ABC=90°
∴ 平行四边形ABCD是矩形
∴ AC=BD
已知:
∴ OB=
验证结论
A
B
C
O
D
求证:
在Rt△ABC中,
如图,
∠ABC=90°,
OB是AC上的中线.
2
1
证明:
延长BO至D,
使OD=OB,
∵ OA=OC, OD=OB
BD
= AC
2
1
2
1
猜想:
直角三角形斜边上的中线等于斜边的一半.
归纳小结
A
B
C
O
直角三角形斜边上的中线定理:
∵ 在Rt△ABC中,
【几何语言】
= AC
2
1
∴ OB
(或 OB=OA=OC, )
点O是斜边AC的中点
或 AC=2OB
直角三角形斜边上的中线等于斜边的一半.
7、如图,在△ABC中,∠ABC = 90°,BD 是斜边 AC 上的中线.
(1) 若 BD=3cm,则AC =_____cm;
(2) 若∠C = 30°,AB =5cm,则AC =_____cm, BD = _____cm.
(3) 若∠C=35°,则 ∠ABD= .
A
B
C
D
6
10
5
巩固练习
55°
8、如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则EF=______cm.
2.5
巩固练习
9、如图,DE 为 △ABC 的中位线,点 F 在 DE 上,且∠AFB=90°,若 AB=5,BC=8,则 EF 的长为 .
1
巩固练习
10、如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.
(1)若AB=10,AC=8,求四边形AEDF的周长;
解:
∵ 在Rt△ADB中,
∵ AD是△ABC的高
∴ DE=
AE
= AB
= ×10
2
1
2
1
∴ ∠ADB=∠ADC=90°
且AB=10
又∵ 在Rt△ADC中,
∴ DF=
AF
= AC
= ×8
2
1
2
1
且AC=8
=5
=4
AE+DE+DF+AF
∴ 四边形AEDF的周长为
点E为斜边AB的中点,
点F为斜边AC的中点,
=5+5+4+4
=18
方法技巧:
可联想直角三角形斜边上的中线的性质进行求解.
当已知条件含有线段的中点、
直角三角形的条件时,
(2) 求证:EF垂直平分AD.
由(1)可得
证明:
∴ E、F在线段AD的垂直平分线上
∴ EF垂直平分AD
DE=AE,DF=AF
(与线段两端距离相等的点在这条线段的垂直平分线上)
10、如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.
(1)若AB=10,AC=8,求四边形AEDF的周长;
11、 如图,已知BD,CE是△ABC不同边上的高,点G,F分别是BC,DE的中点,试说明 GF⊥DE.
解:
∵ 在Rt△BEC 中,
∵ BD,CE 分别为△ABC边上的高
∴ EG=
BC
2
1
∴ ∠BEC=∠BDC=90°
又∵ 在Rt△BDC中,
点G为斜边BC的中点
点G为斜边BC的中点
∴ DG=
BC
2
1
∴ EG=DG
又∵ F为DE的中点
∴ GF⊥DE
连接EG,DG
方法技巧:
可联想直角三角形斜边上的中线的性质进行求解.
当已知条件含有线段的中点、
直角三角形的条件时,
12、如图,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,求PE+PF的值.
A
B
D
C
P
O
E
F
解:
连接OP
∵ 四边形ABCD是矩形
∴ ∠DAB=90°,
OA=OB=OC=OD
∴ S△AOD=S△DOC=S△AOB=S△BOC
4
1
= S矩形ABCD
4
1
= ×6×8=12
∵ 在Rt△ABD中,AB=6,AD=8
∴ BD=
=10
∴ PE+PF=
又∵ S△APO+S△DPO=S△AOD
2
1
2
1
+ ×OD×PF
=12
即
2
1
×5×PE
2
1
+ ×5×PF
=12
∴ OA=OD=5
5
24
∴ ×OA×PE
H
13、如图,将矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=4,求△BED的面积.
解:∵ 四边形ABCD是矩形
∴ AD∥ BC,
∴ ∠2=∠3
由折叠知 ∠1=∠2
∴ ∠1=∠3
∴ BE=DE
设BE=DE=x,
∵ 在Rt△ABE中,AB2+AE2=BE2
∴ 42+(8-x)2=x2,
解得 x=5
∴ S△BED=
矩形的折叠问题常与勾股定理结合考查
∠A=90°
则AE=8-x
即 DE=5
=10
= ×5×4
DE·AB
2
1
2
1
14、如图,点 P 是矩形 ABCD 的对角线 AC 上一点,过点 P 作EF∥BC,分别交 AB,CD 于 E、F,连接 PB、PD.若 AE=2,PF=8.则图中阴影部分的面积为( )
A.10 B.12 C.16 D.18
M
N
15、如图,在矩形ABCD中,点M在DC上,AM=AB,且BN⊥AM,垂足为N.
(1) 求证:△ABN≌△MAD;
(2) 若AD=2,AN=4,求四边形BCMN的面积.
BC=BN
16、如图,在矩形 ABCD 中,AE⊥BD 于 E,∠DAE:∠BAE=3:1,求 ∠BAO 和 ∠EAO 的度数.
A
B
D
C
O
E
∴ ∠DAE=67.5°,
∠BAE=22.5°
∵ AE⊥BD
∴ ∠ABE=
90°-∠BAE
=67.5°
∵ OA=OB
∴ ∠BAO=
∠ABE
=67.5°
∴ ∠EAO=
∠BAO-∠BAE
=67.5°-22.5°
=45°
矩形的两条对角线
知识拓展:
矩形的
每条对角线
把矩形分成两个直角三角形,
将矩形分成四个等腰三角形.
矩形问题
直角三角形和等腰三角形中来解决
转化
本节课你有什么收获?
有一个角是直角的平行四边形叫做矩形.
理解定义
几何语言 :
∵ 在 ABCD中,
∴ ABCD是矩形
反过来
∴ 四边形ABCD是平行四边形,
∵ 四边形ABCD是矩形
注意:
∠A=90°
且∠A=90°
ABCD
∠A=90°
又是它的一个性质.
矩形的定义
既是矩形的一种判定方法,
A
B
D
C
∵ 四边形ABCD是矩形
∴ AC=BD,
矩
形
的
性
质
A
B
D
C
O
矩形的对边平行
矩形的四个角都是直角
且相等.
矩形的
对角线
相等
对角线的性质
边的性质
角的性质
归纳总结
且互相平分
∵ 四边形ABCD是矩形
∴ AB CD,
BC AD
∵ 四边形ABCD是矩形
∴ ∠ABC=∠BCD=∠CDA=∠DAB=90°
且 OA
=OB
=OC
=OD
矩形的两条对角线
知识拓展:
矩形的
每条对角线
把矩形分成两个直角三角形,
将矩形分成四个等腰三角形.
矩形问题
直角三角形和等腰三角形中来解决
转化
归纳小结
A
B
C
O
直角三角形
斜边上的中线
等于
斜边的一半.
直角三角形斜边上的中线定理:
∵ 在Rt△ABC中,,
【几何语言】
= AC
2
1
∴ OB
(或 OB=OA=OC, )
点O是斜边AC的中点
或 AC=2OB
方法技巧:
可联想直角三角形斜边上的中线的性质进行求解.
当已知条件含有线段的中点、
直角三角形的条件时,
