12.2.1作轴对称图形(1)
文档属性
| 名称 | 12.2.1作轴对称图形(1) | 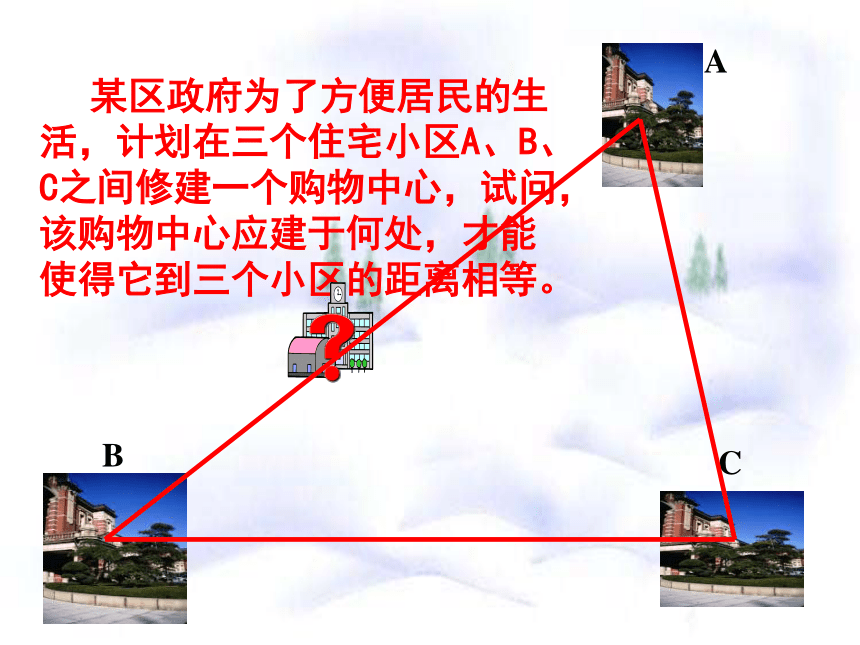 | |
| 格式 | zip | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-25 22:46:24 | ||
图片预览





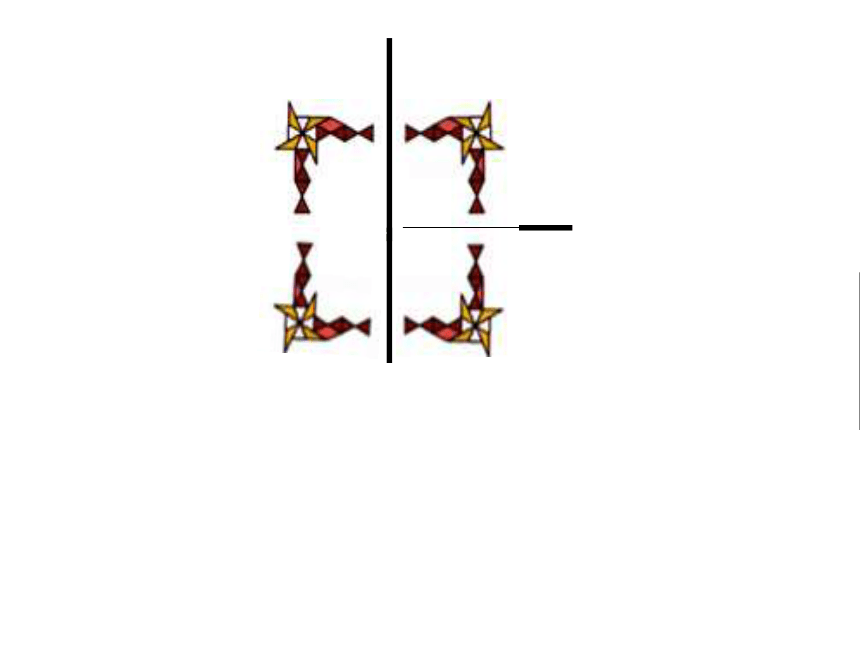
文档简介
(共54张PPT)
·
某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。
A
B
C
2、电信部门要修建一座电视信号发射塔,如图,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条高速公路m、n的距离必须相等,发射塔应建在什么位置?在图上标出它的位置。
P
分析:线段AB的垂直平分线与∠COD的角平分线的交点就是要建发射塔的位置。
C
O
D
P
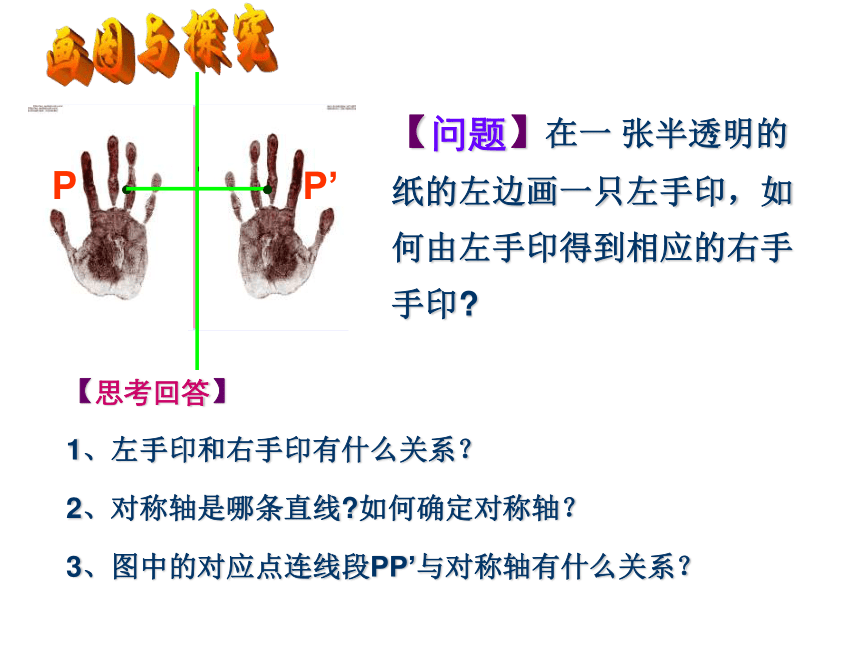
【问题】在一 张半透明的纸的左边画一只左手印,如何由左手印得到相应的右手手印
【思考回答】
1、左手印和右手印有什么关系?
2、对称轴是哪条直线 如何确定对称轴?
3、图中的对应点连线段PP’与对称轴有什么关系?
P’
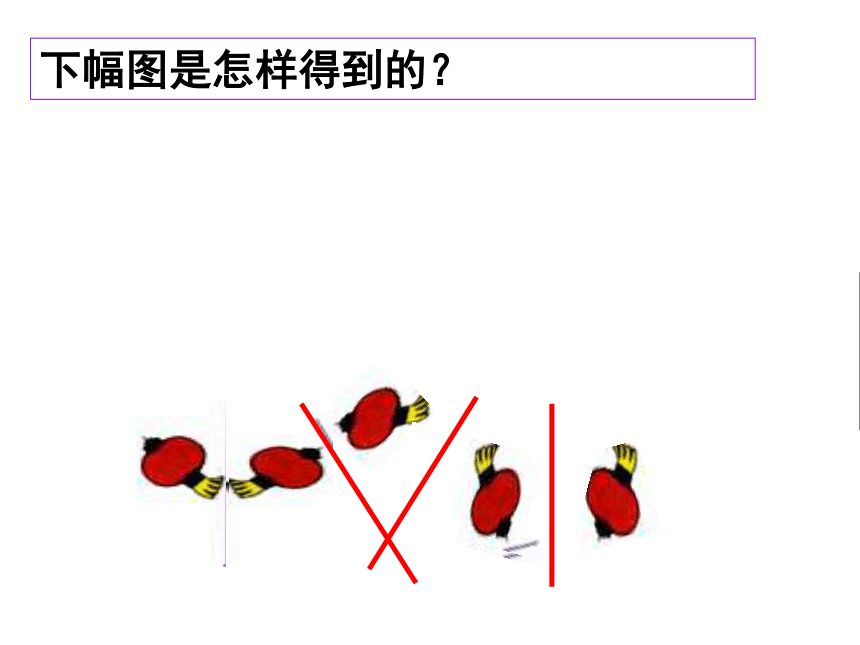
下幅图是怎样得到的?
我们可由一个图形得到与它成轴对称的另一个图形,重复此过程,可得到美丽的图案
下幅图是怎样得到的?
下幅图是怎样得到的?
结论:对称轴的方向和位置发生变化时,得到的图形的方向和位置也发生变化。
重复轴对称过程,你有什么发现?
对称轴的方向和位置发生变化,得到图形的方向和位置也会发生变化.
利用轴对称设计美丽图案
下列美丽图案是怎样形成的?
你能指出它的基本图形吗?
已知对称轴 l 和一个点A,如何画出点A关于 l 的对称点A′
A
A′
O
l
尝试探究
∴点A’就是点A关于直线l的对称点.
如何画线段AB关于直线l 的对称线段A′B′
A
B
A’
B’
∴ 线段A’B’即为所求。
O
例1:如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。
B
A
C
l
∴△A’B’C’即为所求。
A’
B’
C’
O
例1:如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。
B
A
C
B
A
C
l
B’
C’
B
A
C
A’
B’
∴△AB’C’即为所求。
B
A
C
l
∴△A’B’C即为所求。
作已知图形关于已知直线对称的图形的一般步聚:
1、找点
2、画对称点点
3、连线
(确定图形中的一些特殊点);
(连接对称点)。
B
A
C
A’
B’
l
4、写结论
B
A
C
A’
B’
l
想一想:经轴对称所得的图形和原图形全等吗?
轴对称不改变原图形的形状和大小,只改变图形的位置。
图中给出了一个图案的一半,其中的虚线是这个图案的对称轴。
(1)你能猜出整个图案的形状吗?
(2)你能画出这些图案的另一半吗?
猜一猜,画一画
A
B
C
A
A
B
B
C
C
D
E
B
C
C
B
A
C
B
D
E
2、如图给出了一个图案的一半,其中
的虚线 是这个图案的对称轴.
(1)整个图案是个什么形状?
(2)请准确地画出它的另一半.
你可以做得更好!
在由小正方形组成的L形的图中,用三种不同方法添画一个小正方形,使它成为轴对称图形。
你会吗?
通过今天这节课你有什么收获
①对称轴方向和位置发生变化时,得到的图形的方向和位置也会发生变化
②由一个平面图形可以得到它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全一样;
③新图形上的每一点,都是原图形上的某一点关于直线l的对称点;
④连接任意一对对应点的线段都被对称轴垂直平分。
小结:
·
某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。
A
B
C
2、电信部门要修建一座电视信号发射塔,如图,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条高速公路m、n的距离必须相等,发射塔应建在什么位置?在图上标出它的位置。
P
分析:线段AB的垂直平分线与∠COD的角平分线的交点就是要建发射塔的位置。
C
O
D
P
【问题】在一 张半透明的纸的左边画一只左手印,如何由左手印得到相应的右手手印
【思考回答】
1、左手印和右手印有什么关系?
2、对称轴是哪条直线 如何确定对称轴?
3、图中的对应点连线段PP’与对称轴有什么关系?
P’
下幅图是怎样得到的?
我们可由一个图形得到与它成轴对称的另一个图形,重复此过程,可得到美丽的图案
下幅图是怎样得到的?
下幅图是怎样得到的?
结论:对称轴的方向和位置发生变化时,得到的图形的方向和位置也发生变化。
重复轴对称过程,你有什么发现?
对称轴的方向和位置发生变化,得到图形的方向和位置也会发生变化.
利用轴对称设计美丽图案
下列美丽图案是怎样形成的?
你能指出它的基本图形吗?
已知对称轴 l 和一个点A,如何画出点A关于 l 的对称点A′
A
A′
O
l
尝试探究
∴点A’就是点A关于直线l的对称点.
如何画线段AB关于直线l 的对称线段A′B′
A
B
A’
B’
∴ 线段A’B’即为所求。
O
例1:如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。
B
A
C
l
∴△A’B’C’即为所求。
A’
B’
C’
O
例1:如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。
B
A
C
B
A
C
l
B’
C’
B
A
C
A’
B’
∴△AB’C’即为所求。
B
A
C
l
∴△A’B’C即为所求。
作已知图形关于已知直线对称的图形的一般步聚:
1、找点
2、画对称点点
3、连线
(确定图形中的一些特殊点);
(连接对称点)。
B
A
C
A’
B’
l
4、写结论
B
A
C
A’
B’
l
想一想:经轴对称所得的图形和原图形全等吗?
轴对称不改变原图形的形状和大小,只改变图形的位置。
图中给出了一个图案的一半,其中的虚线是这个图案的对称轴。
(1)你能猜出整个图案的形状吗?
(2)你能画出这些图案的另一半吗?
猜一猜,画一画
A
B
C
A
A
B
B
C
C
D
E
B
C
C
B
A
C
B
D
E
2、如图给出了一个图案的一半,其中
的虚线 是这个图案的对称轴.
(1)整个图案是个什么形状?
(2)请准确地画出它的另一半.
你可以做得更好!
在由小正方形组成的L形的图中,用三种不同方法添画一个小正方形,使它成为轴对称图形。
你会吗?
通过今天这节课你有什么收获
①对称轴方向和位置发生变化时,得到的图形的方向和位置也会发生变化
②由一个平面图形可以得到它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全一样;
③新图形上的每一点,都是原图形上的某一点关于直线l的对称点;
④连接任意一对对应点的线段都被对称轴垂直平分。
小结:
