【课件】2.5.1 椭圆的标准方程 数学-RJB-选择性必修第一册-第二章 平面解析几何(共42张PPT)
文档属性
| 名称 | 【课件】2.5.1 椭圆的标准方程 数学-RJB-选择性必修第一册-第二章 平面解析几何(共42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-16 20:45:45 | ||
图片预览











文档简介
(共42张PPT)
数学-RJ·B-选择性必修第一册
2.5.1 椭圆的标准方程
第二章 平面解析几何
重点:椭圆的定义及标准方程
难点:椭圆标准方程的推导,对椭圆定义中的常数加以限制的原因
1.理解椭圆的定义,掌握椭圆的标准方程及其推导过程.
2.会用定义法、待定系数法求椭圆的标准方程.
3.会用坐标法解决问题.
学习目标
知识梳理
一、椭圆的定义
如果F1,F2是平面内的两个定点,a是一个常数,且2a>|F1F2|,
则平面内满足|PF1|+|PF2|=2a的动点P的轨迹称为椭圆,
其中,两个定点F1,F2称为椭圆的焦点,
两个焦点之间的距离|F1F2|称为椭圆的焦距.
【注意】(1)定义中“平面内”不可缺失,否则轨迹就不是椭圆.
(2)动点P满足|PF1|+|PF2|=2a>|F1F2|
时,P的轨迹为椭圆,此式是椭圆的定义表达式,是点P在椭圆上的充要条件;
动点P满足|PF1|+|PF2|=2a=|F1F2|时,P的轨迹为以F1,F2为两端点的线段;
动点P满足|PF1|+|PF2|=2a<|F1F2|时,P的轨迹不存在.
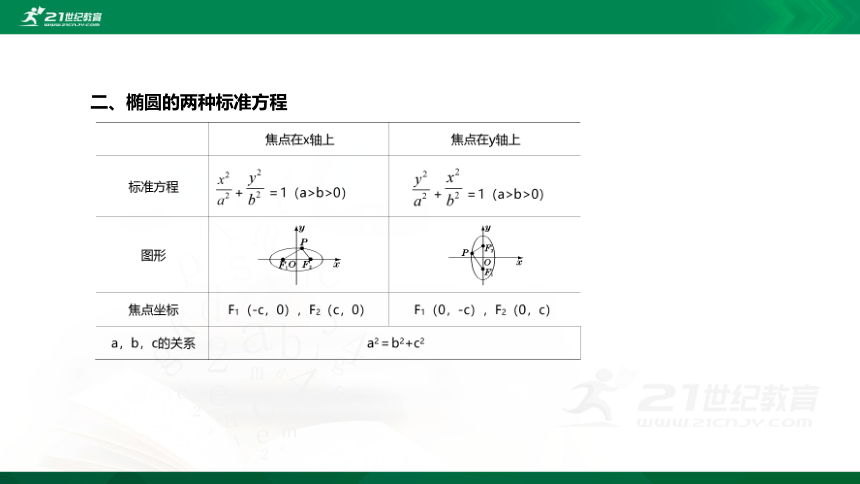
二、椭圆的两种标准方程
[方法技巧]
椭圆的焦点在x轴上 标准方程中含x2项的分母较大;
椭圆的焦点在y轴上 标准方程中含y2项的分母较大.
因此由椭圆的标准方程判断椭圆的焦点位置时,要根据方程中分母的大小来判断,简记为“焦点位置看大小,焦点随着大的跑”.
三、椭圆的一般式方程
对于椭圆标准方程的两种形式,去分母整理之后都可以化成mx2+ny2=1的形式,
但是形如mx2+ny2=1的方程未必表示椭圆,当且仅当m>0,n>0,m≠n时表示椭圆,此时mx2+ny2=1称为椭圆的一般式方程.
常考题型
题组一 椭圆的定义
例 下列命题是真命题的是 .(将所有真命题的序号都填上)
①已知定点F1(-2,0),F2(2,0),则满足|PF1|+|PF2|=的点P的轨迹为椭圆;
②已知定点F1(-3,0),F2(3,0),则满足|PF1|+|PF2|=6的点P的轨迹为线段;
③到定点F1(-5,0),F2(5,0)距离相等的点的轨迹为椭圆;
④若点P到定点F1(-4,0),F2(4,0)的距离的和等于点M(5,3)到定点F1(-4,0),F2(4,0)的距离的和,则点P的轨迹为椭圆.
②④
【解题提示】本题主要考查椭圆的定义,直接利用定义逐一验证即可.
【解析】①因为 <4,所以点P的轨迹不存在;
②因为|F1F2|=6,所以点P的轨迹是线段F1F2;
③到定点F1(-5,0),F2(5,0)距离相等的点的轨迹是线段F1F2的垂直平分线(y轴);
④因为点M(5,3)到定点F1(-4,0),F2(4,0)的距离的和为,所以点P的轨迹为椭圆.
变式训练1-1
已知F1,F2是定点,|F1F2|=8,动点M满足|MF1|+|MF2|=8,则动点M的轨迹是( )
A.椭圆 B.直线 C.圆 D.线段
变式训练1-2
[2020·乌鲁木齐高二检测]已知F1(-2,0),F2(2,0),动点M满足|MF1|+|MF2|=5,则点M的轨迹是 ( )
A. 双曲线 B. 椭圆 C. 线段 D. 不存在
D
B
变式训练1-3
下列命题是真命题的是 .(将所有真命题的序号都填上)
①动点P到两定点A(0,-2),B(0,2)的距离之和为4,则点P的轨迹是椭圆.
②椭圆上一点P与两焦点F1,F2构成△PF1F2的周长为2a+2c.
③△ABC中,B,C坐标为B(-2,0),C(2,0),A为动点,△ABC周长为10,顶点A的轨迹为椭圆(不包括长轴端点).
②③
D
解析:由a2=25,所以椭圆上的点到两个焦点距离之和等于2a=10,
所以到另一个焦点的距离为2a-3=10-3=7.
(0,±3)
6
C
5或3
D
B
C
A
B
C
6
1.椭圆的定义
如果F1,F2是平面内的两个定点,a是一个常数,且2a>|F1F2|,
则平面内满足|PF1|+|PF2|=2a的动点P的轨迹称为椭圆,
其中,两个定点F1,F2称为椭圆的焦点,
两个焦点之间的距离|F1F2|称为椭圆的焦距.
小结
2.椭圆的两种标准方程
图 形
标准方 程
焦 点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
定 义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
(a>c>0)
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJ·B-选择性必修第一册
2.5.1 椭圆的标准方程
第二章 平面解析几何
重点:椭圆的定义及标准方程
难点:椭圆标准方程的推导,对椭圆定义中的常数加以限制的原因
1.理解椭圆的定义,掌握椭圆的标准方程及其推导过程.
2.会用定义法、待定系数法求椭圆的标准方程.
3.会用坐标法解决问题.
学习目标
知识梳理
一、椭圆的定义
如果F1,F2是平面内的两个定点,a是一个常数,且2a>|F1F2|,
则平面内满足|PF1|+|PF2|=2a的动点P的轨迹称为椭圆,
其中,两个定点F1,F2称为椭圆的焦点,
两个焦点之间的距离|F1F2|称为椭圆的焦距.
【注意】(1)定义中“平面内”不可缺失,否则轨迹就不是椭圆.
(2)动点P满足|PF1|+|PF2|=2a>|F1F2|
时,P的轨迹为椭圆,此式是椭圆的定义表达式,是点P在椭圆上的充要条件;
动点P满足|PF1|+|PF2|=2a=|F1F2|时,P的轨迹为以F1,F2为两端点的线段;
动点P满足|PF1|+|PF2|=2a<|F1F2|时,P的轨迹不存在.
二、椭圆的两种标准方程
[方法技巧]
椭圆的焦点在x轴上 标准方程中含x2项的分母较大;
椭圆的焦点在y轴上 标准方程中含y2项的分母较大.
因此由椭圆的标准方程判断椭圆的焦点位置时,要根据方程中分母的大小来判断,简记为“焦点位置看大小,焦点随着大的跑”.
三、椭圆的一般式方程
对于椭圆标准方程的两种形式,去分母整理之后都可以化成mx2+ny2=1的形式,
但是形如mx2+ny2=1的方程未必表示椭圆,当且仅当m>0,n>0,m≠n时表示椭圆,此时mx2+ny2=1称为椭圆的一般式方程.
常考题型
题组一 椭圆的定义
例 下列命题是真命题的是 .(将所有真命题的序号都填上)
①已知定点F1(-2,0),F2(2,0),则满足|PF1|+|PF2|=的点P的轨迹为椭圆;
②已知定点F1(-3,0),F2(3,0),则满足|PF1|+|PF2|=6的点P的轨迹为线段;
③到定点F1(-5,0),F2(5,0)距离相等的点的轨迹为椭圆;
④若点P到定点F1(-4,0),F2(4,0)的距离的和等于点M(5,3)到定点F1(-4,0),F2(4,0)的距离的和,则点P的轨迹为椭圆.
②④
【解题提示】本题主要考查椭圆的定义,直接利用定义逐一验证即可.
【解析】①因为 <4,所以点P的轨迹不存在;
②因为|F1F2|=6,所以点P的轨迹是线段F1F2;
③到定点F1(-5,0),F2(5,0)距离相等的点的轨迹是线段F1F2的垂直平分线(y轴);
④因为点M(5,3)到定点F1(-4,0),F2(4,0)的距离的和为,所以点P的轨迹为椭圆.
变式训练1-1
已知F1,F2是定点,|F1F2|=8,动点M满足|MF1|+|MF2|=8,则动点M的轨迹是( )
A.椭圆 B.直线 C.圆 D.线段
变式训练1-2
[2020·乌鲁木齐高二检测]已知F1(-2,0),F2(2,0),动点M满足|MF1|+|MF2|=5,则点M的轨迹是 ( )
A. 双曲线 B. 椭圆 C. 线段 D. 不存在
D
B
变式训练1-3
下列命题是真命题的是 .(将所有真命题的序号都填上)
①动点P到两定点A(0,-2),B(0,2)的距离之和为4,则点P的轨迹是椭圆.
②椭圆上一点P与两焦点F1,F2构成△PF1F2的周长为2a+2c.
③△ABC中,B,C坐标为B(-2,0),C(2,0),A为动点,△ABC周长为10,顶点A的轨迹为椭圆(不包括长轴端点).
②③
D
解析:由a2=25,所以椭圆上的点到两个焦点距离之和等于2a=10,
所以到另一个焦点的距离为2a-3=10-3=7.
(0,±3)
6
C
5或3
D
B
C
A
B
C
6
1.椭圆的定义
如果F1,F2是平面内的两个定点,a是一个常数,且2a>|F1F2|,
则平面内满足|PF1|+|PF2|=2a的动点P的轨迹称为椭圆,
其中,两个定点F1,F2称为椭圆的焦点,
两个焦点之间的距离|F1F2|称为椭圆的焦距.
小结
2.椭圆的两种标准方程
图 形
标准方 程
焦 点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
定 义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
(a>c>0)
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
