【课件】1.2空间向量在立体几何中的应用 1.2.3直线与平面的夹角 1.2.4二面角 1.2.5空间中的距离 数学-RJ·B-选择性必修第一册 第一章 空间向量与立体几何 (共65张PPT)
文档属性
| 名称 | 【课件】1.2空间向量在立体几何中的应用 1.2.3直线与平面的夹角 1.2.4二面角 1.2.5空间中的距离 数学-RJ·B-选择性必修第一册 第一章 空间向量与立体几何 (共65张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-16 00:00:00 | ||
图片预览











文档简介
(共65张PPT)
数学-RJ·B-选择性必修第一册
1.2 空间向量在立体几何中的应用
1.2.3 直线与平面的夹角
1.2.4 二面角
1.2.5 空间中的距离
第一章 空间向量与立体几何
重点:斜线和平面所成的角,二面角的概念与求法,四种距离的概念,点到平面距离的求法
难点:斜线和平面所成角的求解,公式cos θ=cos θ1cos θ2的灵活运用,二面角大小的求法,求平面的法向量
1.理解直线与平面所成角的概念,会用向量法求线面角.
2.正确区分向量夹角与所求线面角及面面角的关系.
3.掌握求二面角的基本方法和步骤,会求二面角的大小.
4.理解点到平面距离的概念,能灵活运用向量方法求各种距离,体会向量法在求距离中的作用.
学习目标
知识梳理
1.线面角
平面的斜线与它在平面内的射影所成的锐角,称为这条斜线与平面所成的角.
如图,记∠AOA′=θ1,∠A′OM=θ2,∠AOM=θ,
则cos θ=cos θ1cos θ2.
一般地,因为0≤cos θ2≤1,所以由上式可知cos θ≤cos θ1,
因为θ1和θ都是锐角,所以可得θ1≤θ.
这就是说,平面的斜线与平面所成的角,是斜线和这个平面内所有直线所成角中最小的角.
如果v是直线l的一个方向向量,n是平面α的一个法向量,设直线l与平面α所成角的大小为θ,
θ=-〈v,n〉,θ=〈v,n〉-,
特别地,cos θ=sin〈v,n〉,sin θ=|cos〈v,n〉|.
(1) (2)
从一条直线出发的两个半平面所组成的图形称为二面角,
这条直线称为二面角的棱,这两个半平面称为二面角的面.
如图所示,在二面角α-l-β的棱上任取一点O,以O为垂足,分别在半平面α和β内作垂直于棱的射线OA和OB,则射线OA和OB所成的角称为二面角的平面角.二面角的大小用它的平面角大小来度量,即二面角大小等于它的平面角大小.特别地,平面角是直角的二面角称为直二面角.
2.二面角
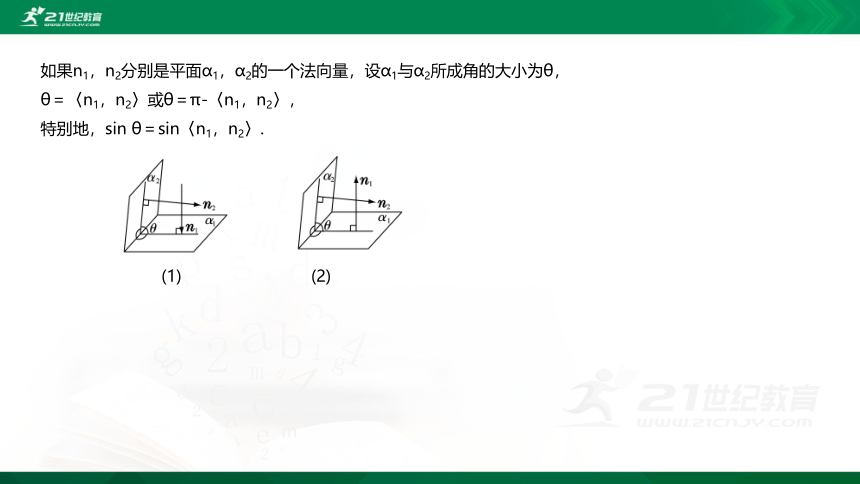
如果n1,n2分别是平面α1,α2的一个法向量,设α1与α2所成角的大小为θ,
θ=〈n1,n2〉或θ=π-〈n1,n2〉,
特别地,sin θ=sin〈n1,n2〉.
(1) (2)
一般地,若A是平面α外一点,B是平面α内一点,n是平面α的一个法向量,则
点A到平面α的距离d= .
3.空间中的距离
常考题型
一 直线与平面的夹角
<1>用最小角定理求直线与平面所成的角
例1
【变式训练】
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是B1C1和CC1的中点,求异面直线A1B与EF所成角的余弦值.
解题方法:
应用最小角定理解题的过程
1.明确三线:平面内的直线、平面的斜线、斜线在平面内的射影.
2.明确三角:斜线与平面内的直线所成的角为θ,斜线与射影所成的角为θ1,射影与平面内的直线所成的角为θ2.
3.应用定理求解.
例2
<2>用空间向量求直线与平面所成的角
【变式训练】
1如图,菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=2,CF=3.若直线FO与平面BED所成的角为45°,则AE= .
D
2
解题方法:
<3>已知直线与平面所成角,用向量法求参数
例3
【变式训练】
如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD中,
AB⊥AD,AB+AD=4,CD=,∠CDA=45°.
(1)求证:平面PAB⊥平面PAD.
(2)设AB=AP,若直线PB与平面PCD所成的角为30°,求线段AB的长.
解题方法:
二 二面角及其度量
如图,已知四边形ABCD是正方形,PA⊥平面ABCD.
(1)求二面角B-PA-D平面角的度数;
(2)求二面角B-PA-C平面角的度数.
例4
【解】 (1)∵ PA⊥平面ABCD,∴ AB⊥PA,AD⊥PA.
∴ ∠BAD为二面角B-PA-D的平面角.
又由题意∠BAD=90°,∴ 二面角B-PA-D平面角的度数为90°.
(2)∵ PA⊥平面ABCD,∴ AB⊥PA,AC⊥PA.∴ ∠BAC为二面角B-PA-C的平面角.又四边形ABCD为正方形,∴ ∠BAC=45°.
即二面角B-PA-C平面角的度数为45°.
【变式训练】
A
三 用空间向量求二面角的大小
<1>用方向向量法求二面角
【变式训练】
若向量m=(-1,2,0),n=(3,0,-2)都与一个二面角的棱垂直,且m,n
分别与两个半平面平行,则该二面角的余弦值为 .
<2>用法向量求二面角
(1)【证明】 由已知∠BAP=∠CDP=90°,得AB⊥AP,CD⊥PD.
由于AB∥CD,故AB⊥PD.又PA∩PD=P,所以AB⊥平面PAD.
又AB?平面PAB,所以平面PAB⊥平面PAD.
【变式训练】
【变式训练】
解:以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),B(2,0,0),C(0,2,0),D(1,1,0),A1(0,0,4),C1(0,2,4).
解题方法:
例7
四 向量法解决二面角相关的存在性、探究性问题
【变式训练】
解题方法:
用空间向量求解探索性问题的策略
对于立体几何中的探索性问题,由于此类问题涉及的点具有不确定性,用传统方法解决难度较大,向量方法(特别是坐标法)可使几何问题代数化,思路简单,操作方便.解决此类问题的基本步骤:
1.假设题中的数学对象存在(或结论成立)或暂且认可其中的一部分结论.
2.在这个前提下进行逻辑推理,把要成立的结论当作条件,据此列方程或方程组,把“是否存在”问题转化为“点的坐标(或参数)是否有解,是否有规定范围内的解”等.若由此推导出矛盾,则否定假设;否则,给出肯定结论.
例8
五 空间中的距离
<1>空间中两点之间的距离
已知平行六面体ABCD-A′B′C′D′中,AB=4,AD=3,AA′=5,∠BAD=90°,∠BAA′=∠DAA′=60°,则AC′= .
【变式训练】
例9
<2>点到直线的距离
[2020·河北衡水中学高二检测]如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为 .
例10
<3>点到平面的距离
已知正方形ABCD的边长为1,PD⊥平面ABCD,且PD=1,E,F分别为AB,BC的中点.求点D到平面PEF的距离.
【解】 建立以D为坐标原点,DA,DC,DP分别为x轴,y轴,z轴的空间直角坐标系,如图所示.
【变式训练】
解题方法:
另外,也可以求出点A在平面内的射影,用两点间的距离公式求解.
例11
<4>相互平行的直线与平面之间、相互平行的平面与平面之间的距离
已知正方形ABCD的边长为1,PD⊥平面ABCD,且PD=1,E,F分别为AB,BC的中点.求直线AC到平面PEF的距离.
【变式训练】
解题方法:
1.当直线与平面平行时,要求直线到平面的距离,需要在直线上任取一点(端点或中点等),求出该点到平面的距离即可.
2.当平面与平面平行时,要求两个平面之间的距离,需在一个平面内找到一点,求出该点到另一个平面的距离即可.
小结
1.线面角
如图,记∠AOA′=θ1,∠A′OM=θ2,∠AOM=θ,
则cos θ=cos θ1cos θ2.
如果n1,n2分别是平面α1,α2的一个法向量,设α1与α2所成角的大小为θ,
θ=〈n1,n2〉或θ=π-〈n1,n2〉,
特别地,sin θ=sin〈n1,n2〉.
(1) (2)
2.二面角
一般地,若A是平面α外一点,B是平面α内一点,n是平面α的一个法向量,则
点A到平面α的距离d= .
3.空间中的距离
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJ·B-选择性必修第一册
1.2 空间向量在立体几何中的应用
1.2.3 直线与平面的夹角
1.2.4 二面角
1.2.5 空间中的距离
第一章 空间向量与立体几何
重点:斜线和平面所成的角,二面角的概念与求法,四种距离的概念,点到平面距离的求法
难点:斜线和平面所成角的求解,公式cos θ=cos θ1cos θ2的灵活运用,二面角大小的求法,求平面的法向量
1.理解直线与平面所成角的概念,会用向量法求线面角.
2.正确区分向量夹角与所求线面角及面面角的关系.
3.掌握求二面角的基本方法和步骤,会求二面角的大小.
4.理解点到平面距离的概念,能灵活运用向量方法求各种距离,体会向量法在求距离中的作用.
学习目标
知识梳理
1.线面角
平面的斜线与它在平面内的射影所成的锐角,称为这条斜线与平面所成的角.
如图,记∠AOA′=θ1,∠A′OM=θ2,∠AOM=θ,
则cos θ=cos θ1cos θ2.
一般地,因为0≤cos θ2≤1,所以由上式可知cos θ≤cos θ1,
因为θ1和θ都是锐角,所以可得θ1≤θ.
这就是说,平面的斜线与平面所成的角,是斜线和这个平面内所有直线所成角中最小的角.
如果v是直线l的一个方向向量,n是平面α的一个法向量,设直线l与平面α所成角的大小为θ,
θ=-〈v,n〉,θ=〈v,n〉-,
特别地,cos θ=sin〈v,n〉,sin θ=|cos〈v,n〉|.
(1) (2)
从一条直线出发的两个半平面所组成的图形称为二面角,
这条直线称为二面角的棱,这两个半平面称为二面角的面.
如图所示,在二面角α-l-β的棱上任取一点O,以O为垂足,分别在半平面α和β内作垂直于棱的射线OA和OB,则射线OA和OB所成的角称为二面角的平面角.二面角的大小用它的平面角大小来度量,即二面角大小等于它的平面角大小.特别地,平面角是直角的二面角称为直二面角.
2.二面角
如果n1,n2分别是平面α1,α2的一个法向量,设α1与α2所成角的大小为θ,
θ=〈n1,n2〉或θ=π-〈n1,n2〉,
特别地,sin θ=sin〈n1,n2〉.
(1) (2)
一般地,若A是平面α外一点,B是平面α内一点,n是平面α的一个法向量,则
点A到平面α的距离d= .
3.空间中的距离
常考题型
一 直线与平面的夹角
<1>用最小角定理求直线与平面所成的角
例1
【变式训练】
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是B1C1和CC1的中点,求异面直线A1B与EF所成角的余弦值.
解题方法:
应用最小角定理解题的过程
1.明确三线:平面内的直线、平面的斜线、斜线在平面内的射影.
2.明确三角:斜线与平面内的直线所成的角为θ,斜线与射影所成的角为θ1,射影与平面内的直线所成的角为θ2.
3.应用定理求解.
例2
<2>用空间向量求直线与平面所成的角
【变式训练】
1如图,菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=2,CF=3.若直线FO与平面BED所成的角为45°,则AE= .
D
2
解题方法:
<3>已知直线与平面所成角,用向量法求参数
例3
【变式训练】
如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD中,
AB⊥AD,AB+AD=4,CD=,∠CDA=45°.
(1)求证:平面PAB⊥平面PAD.
(2)设AB=AP,若直线PB与平面PCD所成的角为30°,求线段AB的长.
解题方法:
二 二面角及其度量
如图,已知四边形ABCD是正方形,PA⊥平面ABCD.
(1)求二面角B-PA-D平面角的度数;
(2)求二面角B-PA-C平面角的度数.
例4
【解】 (1)∵ PA⊥平面ABCD,∴ AB⊥PA,AD⊥PA.
∴ ∠BAD为二面角B-PA-D的平面角.
又由题意∠BAD=90°,∴ 二面角B-PA-D平面角的度数为90°.
(2)∵ PA⊥平面ABCD,∴ AB⊥PA,AC⊥PA.∴ ∠BAC为二面角B-PA-C的平面角.又四边形ABCD为正方形,∴ ∠BAC=45°.
即二面角B-PA-C平面角的度数为45°.
【变式训练】
A
三 用空间向量求二面角的大小
<1>用方向向量法求二面角
【变式训练】
若向量m=(-1,2,0),n=(3,0,-2)都与一个二面角的棱垂直,且m,n
分别与两个半平面平行,则该二面角的余弦值为 .
<2>用法向量求二面角
(1)【证明】 由已知∠BAP=∠CDP=90°,得AB⊥AP,CD⊥PD.
由于AB∥CD,故AB⊥PD.又PA∩PD=P,所以AB⊥平面PAD.
又AB?平面PAB,所以平面PAB⊥平面PAD.
【变式训练】
【变式训练】
解:以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),B(2,0,0),C(0,2,0),D(1,1,0),A1(0,0,4),C1(0,2,4).
解题方法:
例7
四 向量法解决二面角相关的存在性、探究性问题
【变式训练】
解题方法:
用空间向量求解探索性问题的策略
对于立体几何中的探索性问题,由于此类问题涉及的点具有不确定性,用传统方法解决难度较大,向量方法(特别是坐标法)可使几何问题代数化,思路简单,操作方便.解决此类问题的基本步骤:
1.假设题中的数学对象存在(或结论成立)或暂且认可其中的一部分结论.
2.在这个前提下进行逻辑推理,把要成立的结论当作条件,据此列方程或方程组,把“是否存在”问题转化为“点的坐标(或参数)是否有解,是否有规定范围内的解”等.若由此推导出矛盾,则否定假设;否则,给出肯定结论.
例8
五 空间中的距离
<1>空间中两点之间的距离
已知平行六面体ABCD-A′B′C′D′中,AB=4,AD=3,AA′=5,∠BAD=90°,∠BAA′=∠DAA′=60°,则AC′= .
【变式训练】
例9
<2>点到直线的距离
[2020·河北衡水中学高二检测]如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为 .
例10
<3>点到平面的距离
已知正方形ABCD的边长为1,PD⊥平面ABCD,且PD=1,E,F分别为AB,BC的中点.求点D到平面PEF的距离.
【解】 建立以D为坐标原点,DA,DC,DP分别为x轴,y轴,z轴的空间直角坐标系,如图所示.
【变式训练】
解题方法:
另外,也可以求出点A在平面内的射影,用两点间的距离公式求解.
例11
<4>相互平行的直线与平面之间、相互平行的平面与平面之间的距离
已知正方形ABCD的边长为1,PD⊥平面ABCD,且PD=1,E,F分别为AB,BC的中点.求直线AC到平面PEF的距离.
【变式训练】
解题方法:
1.当直线与平面平行时,要求直线到平面的距离,需要在直线上任取一点(端点或中点等),求出该点到平面的距离即可.
2.当平面与平面平行时,要求两个平面之间的距离,需在一个平面内找到一点,求出该点到另一个平面的距离即可.
小结
1.线面角
如图,记∠AOA′=θ1,∠A′OM=θ2,∠AOM=θ,
则cos θ=cos θ1cos θ2.
如果n1,n2分别是平面α1,α2的一个法向量,设α1与α2所成角的大小为θ,
θ=〈n1,n2〉或θ=π-〈n1,n2〉,
特别地,sin θ=sin〈n1,n2〉.
(1) (2)
2.二面角
一般地,若A是平面α外一点,B是平面α内一点,n是平面α的一个法向量,则
点A到平面α的距离d= .
3.空间中的距离
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
