【课件】2.2直线及其方程 2.2.1直线的倾斜角与斜率 数学-RJB-选择性必修第一册-第二章 平面解析几何 (共62张PPT)
文档属性
| 名称 | 【课件】2.2直线及其方程 2.2.1直线的倾斜角与斜率 数学-RJB-选择性必修第一册-第二章 平面解析几何 (共62张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-16 20:59:41 | ||
图片预览










文档简介
(共62张PPT)
数学-RJ·B-选择性必修第一册
2.2 直线及其方程
2.2.1 直线的倾斜角与斜率
第二章 平面解析几何
重点:理解直线的斜率的概念,探索如何通过直线上两点求直线的斜率
难点:理解斜率的几何意义及其与“相似比”等概念之间的内在联系
1.理解直线的倾斜角和斜率的概念.
2.理解直线斜率的几何意义;掌握倾斜角与斜率的对应关系.
3.掌握过两点的直线的斜率公式.
学习目标
知识梳理
1.直线的倾斜角与斜率
一般地,给定平面直角坐标系中的一条直线,如果这条直线与x轴相交,将x轴绕着它们的交点按逆时针方向旋转到与直线重合时所转的最小正角记为θ,则称θ为这条直线的倾斜角.
倾斜角的取值范围是 (即 ).
特别地,与x轴平行或重合(即与y轴垂直)的直线,倾斜角为 ,与x轴垂直的直线,倾斜角为 .
[0°,180°)
[0,π)
0°
90°
一般地,如果直线l的倾斜角为θ,则当θ≠90°时,称k=tan θ为直线l的斜率;当θ=90°时,称直线l的斜率不存在.
若A(x1,y1),B(x2,y2)是直线l上两个不同的点,则当x1≠x2时,直
线l的斜率为k= ,当x1=x2时,直线l的斜率不存在.
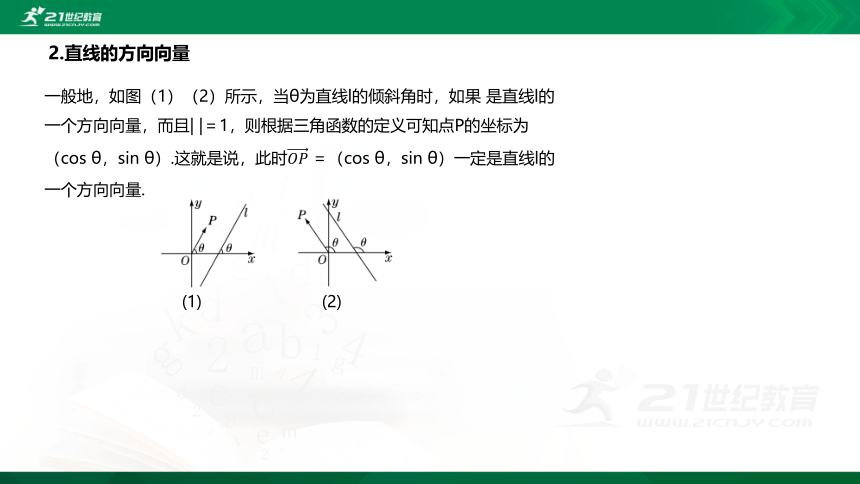
2.直线的方向向量
一般地,如图(1)(2)所示,当θ为直线l的倾斜角时,如果 是直线l的一个方向向量,而且| |=1,则根据三角函数的定义可知点P的坐标为
(cos θ,sin θ).这就是说,此时=(cos θ,sin θ)一定是直线l的一个方向向量.
(1) (2)
当然,此时对于任意的实数λ≠0,=(λcos θ,λsin θ)也是直线l的一
个方向向量.当θ≠90°时,直线的斜率k是存在的,而且k=tan θ= ,
因此,此时如果令λ=,则可知(1,k)也一定是直线l的一个方向向量.
一般地,如果已知a=(u,v)为直线l的一个方向向量,则:
(1)当u=0时,显然直线l的斜率不存在,倾斜角为90°;
(2)当u≠0时,直线l的斜率是存在的,而且此时(1,k)与a=(u,v)都是直线l的一个方向向量,由直线的任意两个方向向量共线可知1×v=k×u,从而k=,因此可知倾斜角满足tan θ= .
直线l的方向向量不唯一,直线l的所有方向向量共线.
3.直线的法向量
一般地,如果表示非零向量v的有向线段所在直线与直线l垂直,则称向量v为直线l的一个法向量,记作v⊥l.
一条直线的方向向量与法向量 .
特别地,当x0与y0不全为0时,因为向量(x0,y0)与(y0,-x0)是互相垂直的,所以,如果其中一个为直线l的一个方向向量,则另一个一定是直线l的一个法向量.
常考题型
题组一 直线的倾斜角
<1>识别直线的倾斜角
例1 图中直线的倾斜角标注正确的有 个.
(1) (2) (3) (4)
【解析】 对于(1),角α的一边取的是x轴的负方向,因此标注不正确;对于(2),角α的一边取的是直线向下的方向,因此标注不正确;对于(3),角α的两边分别取的是x轴的负方向和直线向下的方向,因此标注不正确;对于(4),角α是y轴正方向与直线向上方向所成的角,因此标注不正确.故标注正确的有0个.
【答案】 0
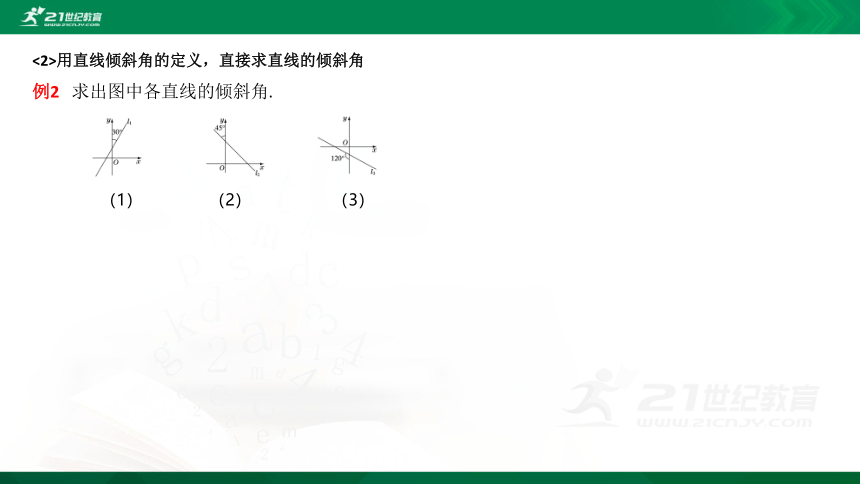
<2>用直线倾斜角的定义,直接求直线的倾斜角
例2 求出图中各直线的倾斜角.
(1) (2) (3)
【解】(1)如图(1),可知∠OAB为直线l1的倾斜角,易知∠ABO=30°,
∴ ∠OAB=60°,即直线l1的倾斜角为60°.
(2)如图2-2-3(2),可知∠xAB为直线l2的倾斜角,易知∠OBA=45°,
∴ ∠OAB=45°,∴ ∠xAB=135°,即直线l2的倾斜角为135°.
(3)如图(3),可知∠OAC为直线l3的倾斜角,易知∠ABO=60°,∴ ∠BAO=30°,∴ ∠OAC=150°,即直线l3的倾斜角为150°.
(1) (2) (3)
【变式训练】
设直线l过原点,其倾斜角为α,将直线l绕坐标原点按逆时针方向旋转30°,得到直线l1,则直线l1的倾斜角为 ( )
A.α+30°
B.α-150°
C.150°-α
D.当0°≤α<150°时为α+30°,当150°≤α<180°时为α-150°
<3>已知两点坐标,求其所在直线的倾斜角
例3 已知a,b,c是三个互不相等的实数,求经过下列两点的直线的倾斜角.
(1)A(a,c),B(b,c);(2)C(a,b),D(a,c);
(3)P(b,b+c),Q(a,c+a).
【解】 (1)因为点A,B的纵坐标相等均为c,所以直线AB的倾斜角为0°.
(2)因为点C,D的横坐标相等均为a,所以直线CD的倾斜角为90°.
(3)设直线PQ的倾斜角为θ,则tan θ==1,所以直线PQ的倾斜角为45°.
【变式训练】
已知坐标平面内三点A(-1,1),B(1,1),C(2,+1).求直线AB,BC,AC的倾斜角.
解:设直线AB,BC,AC的倾斜角分别为θ1,θ2,θ3,
则tan θ1==0,tan θ2= =,tan θ3= =.
∵ 倾斜角的取值范围是[0°,180°),
又∵ tan 0°=0,tan 60°= ,tan 30°= ,
∴ AB的倾斜角θ1=0°,BC的倾斜角θ2=60°,AC的倾斜角θ3=30°.
解题方法:
已知不同两点A(x1,y1),B(x2,y2),求这两点所在直线的倾斜角α的取值范围时,要注意分别考虑四种情况:
(1)当x1=x2时,α=90°;
(2)当y1=y2时,α=0°;
(3)当tan α=>0时,α∈(0°,90°);
(4)当tan α= <0时,α∈(90°,180°).
<4>已知两点含参坐标,在其所在直线倾斜角大小限制条件下,求参数
例4 已知M(2m+3,m),N(m-2,1),
(1)当m为何值时,直线MN的倾斜角为锐角?
(2)当m为何值时,直线MN的倾斜角为钝角?
(3)当m为何值时,直线MN的倾斜角为直角?
【解】 (1)因为点A,B的纵坐标相等均为c,所以直线AB的倾斜角为0°.
(2)因为点C,D的横坐标相等均为a,所以直线CD的倾斜角为90°.
(3)设直线PQ的倾斜角为θ,则tan θ==1,所以直线PQ的倾斜角为45°.
【解】 设直线MN的倾斜角为θ,
(1)直线MN的倾斜角为锐角?tan θ>0,即>0,解得m>1或m<-5.
(2)直线MN的倾斜角为钝角?tan θ<0,即<0,解得-5(3)直线MN的倾斜角为直角?点M,N的横坐标相等,即2m+3=m-2,解得m=-5.
已知直线l经过点A(1,t)和B(-2,1),试问,当t取何值时,直线l的倾斜角α为(1)45°;(2)60°;(3)120°?
【变式训练】
解:(1)因为直线l的倾斜角α=45°,且tan 45°=1,
所以tan α=tan 45°===1,解得t=4.
(2)因为直线l的倾斜角α=60°,且tan 60°=,所以tan α=tan 60°= == ,解得t= +1.
已知直线l经过点A(1,t)和B(-2,1),试问,当t取何值时,直线l的倾斜角α为(1)45°;(2)60°;(3)120°?
【变式训练】
(3)因为直线l的倾斜角α=120°,且tan 120°=- ,
所以tan α=tan 120°= ==- ,
解得t=1- .
<5>已知一点坐标,在限定范围内,求其所在直线倾斜角的取值范围
例5 [2020·福建三明高一段考]已知两点A(-4,+1),B(3,2),过点P(2,1)的直线l与线段AB有公共点,求直线l的倾斜角α的取值范围.
【解】 如图所示,过点P,A作直线PA,过点P,B作直线PB.
∵ =,=1,
∴ 直线PA的倾斜角为α1=150°,直线PB的倾斜角为α2=45°.
∵ 直线l与线段AB有公共点,
∴ 由图形易得直线l的倾斜角α的取值范围为45°≤α≤150°.
已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点,求l的倾斜角α的取值范围.
【变式训练】
解:设直线PA的倾斜角为θ1,直线PB的倾斜角为θ2,如图,
∵ tan θ1==-1,tan θ2==1,
∴ PA的倾斜角θ1=135°,PB的倾斜角θ2=45°.
又直线l的倾斜角介于直线PB与PA的倾斜角之间,
∴ 直线l的倾斜角α的取值范围是45°≤α≤135°.
<6>已知两点含参坐标,求其所在直线倾斜角的取值范围
例6 求经过A(m,3),B(1,2)两点的直线的倾斜角α的取值范围.
【解】 当m=1时,直线AB的倾斜角α=90°;
当m>1时,因为>0,所以直线AB的倾斜角α的取值范围是0°<α<90°;
当m<1时,因为<0,所以直线AB的倾斜角α的取值范围是90°<α<180°.
综上,当m=1时,α=90°;
当m>1时,0°<α<90°;当m<1时,90°<α<180°.
[2020·河南项城高一检测]已知两点A(-1,2),B(m,3),实数m∈,求直线AB的倾斜角α的取值范围.
【变式训练】
解:当m=-1时,α=90°;
当m∈ 时,tan α=∈(-∞,-],此时α∈(90°,120°];
当m∈(-1, -1]时,tan α= ∈ ,此时α∈[30°,90°).
综上所述,倾斜角α的取值范围为[30°,120°].
题组二 直线的斜率
<1>已知直线的斜率,求其倾斜角
例7 已知直线l的斜率为-1,则它的倾斜角为 .
【解析】 设直线l的倾斜角为α,0°≤α<180°,则tan α=-1,所以α=135°.
【答案】 135°
<2>已知两点含参坐标,在其所在直线的斜率大小限制条件下,求参数
例8 已知一条直线经过点A(-a,6),B(1,3a),且斜率为12,求a的值.
【解】 由题意得=12,即3a-6=12+12a(a≠-1),解得a=-2.
【注意】 已知直线的斜率为12,因此不用考虑-a=1(即x1=x2)的情况.
已知经过两点A(5,m)和B(m,8)的直线的斜率大于1,求实数m的取值范围.
【变式训练】
解:由题意得>1,∴ -1>0,
∴ >0,即<0,∴ 5<3>已知直线的倾斜角,求斜率
例9 若直线AB与y轴的夹角为60°,则直线AB的倾斜角为 ,斜率为 .
解析:不妨设直线AB过原点,如图,直线AB的倾斜角为30°或150°,其斜率为 或- .
答案: 30°或150° 或-
[2020·江苏南京高二检测]已知直线AB的斜率为-,直线l的倾斜角是直线AB的倾斜角的一半,求直线l的斜率.
【变式训练】
解:∵ 直线AB的斜率kAB=- ,∴ 直线AB的倾斜角是120°,∴ 直线l的倾斜角是60°,∴ 直线l的斜率k=tan 60°= .
<4>已知两点坐标,求其所在直线的斜率
例10 经过下列两点的直线的斜率k是否存在?若存在,求其斜率;若不存在,说明理由.
(1)(1,-1),(-3,2);(2)(1,-2),(5,-2);
(3)(3,4),(-2,-5);(4)(3,0),(3,).
【解】 (1)存在.k==-.(2)存在.k= =0.
(3)存在.k= =.(4)不存在.理由:∵ x1=x2,∴ k不存在.
如图所示,直线l1,l2,l3都经过点P(3,2),又l1,l2,l3分别经过点Q1(-2,-1),Q2(4,-2),Q3(-3,2),计算直线l1,l2,l3的斜率,并判断这些直线的倾斜角是锐角还是钝角.
【变式训练】
解:设k1,k2,k3分别表示直线l1,l2,l3的斜率.
因为Q1,Q2,Q3的横坐标与P点的横坐标均不相等,
所以k1==,k2= =-4,k3= =0.
由k1>0知直线l1的倾斜角为锐角;
由k2<0知直线l2的倾斜角为钝角;
由k3=0知直线l3的倾斜角为0°,既不是锐角也不是钝角.
<5>已知两点含参坐标,求其所在直线的斜率
例11 [2019·甘肃武威高一检测]求过下列两点的直线的斜率k.
(1)A(a,b),B(ma,mb)(m≠1,a≠0);
(2)P(2,1),Q(m,2).
【解题提示】 已知直线上两点A(x1,y1),B(x2,y2),当x1≠x2时,k= ;当x1=x2时,k不存在.
【解】 (1)∵ m≠1,a≠0,∴ k== .
(2)当m=2时,直线与x轴垂直,斜率k不存在;当m≠2时,k==.
经过下列两点的直线的斜率是否存在?若存在,求其斜率;若不存在,说明理由.
(1)A(3,2),B(5,-6);
(2)E(2,-3),F(m,-2)(m∈R).
【变式训练】
解:(1)因为3≠5,所以直线的斜率存在,kAB==-4.
(2)当m=2时,直线的斜率不存在;当m≠2时,直线的斜率存在,且kEF==.
<6>已知直线的倾斜角大小,判断其斜率的大小
例12 如图,已知直线l1,l2,l3的斜率分别为k1,k2,k3,则k1,k2,k3之间的大小关系为 (按从大到小的顺序排列).
【解题提示】 根据直线的倾斜程度判断倾斜角
是锐角还是钝角,进而比较斜率的大小.
【解析】 由图可知直线l1的倾斜角为钝角,所以k1<0;直线l2与直线l3的倾斜角均为锐角,且直线l2的倾斜角较大,所以k2>k3>0,所以k2>k3>k1.
【答案】 k2>k3>k1
如图所示,设k1,k2,k3分别为直线l1,l2,l3的斜率,则k1,k2,k3的大小关系
是 .
【变式训练】
解析:设直线l1,l2,l3的倾斜角分别为α1,α2,α3,
则由题图可知0°<α1<90°<α3<α2<180°,因此k3即k3答案: k3<7>已知一点坐标,在限定范围内,求其所在直线的斜率的取值范围
例13 [2019·天津高一检测]已知坐标平面内三点A(-1,1),B(1,1),C(2,+1).
(1)求直线AB,BC,AC的斜率.
(2)若D为△ABC的边AB上一动点,求直线CD的斜率k的取值范围.
【解题提示】 (1)利用k=(x1≠x2)求解;
(2)先求出AC,BC的斜率,进而求出k的范围.
【解】 (1)由斜率公式得kAB==0,kBC= =,
kAC= =.
(2)如图,当直线CD由CA逆时针方向旋转到CB时,直线CD与AB恒有交点,即D在线段AB上,此时k由kCA增大到kCB,所以k的取值范围为 .
[2020·浙江嘉兴一中高二检测]过点P(-1,2)的直线l与线段AB相交,且A(-2,-3),B(3,0),求直线l的斜率k的取值范围.
【变式训练】
解:如图,kPA==5,kPB== .取C点为(-1,0).
过点P且与x轴垂直的直线PC与线段AB相交,但此时直线l的斜率不存在.在直线l由PA绕P点逆时针旋转到PC(不包括PC)处的过程中,l的斜率始终为正,且逐渐增大,此时直线l的斜率k的范围是[5,+∞).在直线l由PC(不包括PC)绕P点逆时针旋转到PB处的过程中,斜率为负且逐渐变大,此时l的斜率k的范围是.
故直线l的斜率k的取值范围是∪[5,+∞).
题组三 从直线的倾斜角、斜率角度,解决三点共线问题
<1>从直线的倾斜角、斜率角度,证明三点共线
例14 求证:三点A(-2,3),B(7,6),C(4,5)在同一直线上.
【解题提示】 (1)因为一个定点和斜率就可确定一条直线,所以要证这三点共线,只需证任意两点所连直线的斜率相等即可.
(2)当直线的斜率存在时,A,B,C三点共线等价于kAB=kAC或kAB=kBC或kAC=kBC.
【证明】 ∵ A(-2,3),B(7,6),C(4,5),
∴ kAB== ,kAC= =.∴ kAB=kAC.
又直线AB、直线AC均过点A,∴ 直线AB,AC重合,即A,B,C三点共线.
求证:A(1,-1),B(-2,-7),C(0,-3)三点共线.
【变式训练】
解:∵ A(1,-1),B(-2,-7),C(0,-3),
∴ kAB==2,kAC= =2,则kAB=kAC.
∵ 直线AB与直线AC过同一点A且斜率相同,
∴ 直线AB与直线AC为同一条直线,
故A,B,C三点共线.
<2>从直线的倾斜角、斜率角度,已知三点共线,求参数
例15 如果,B(4,-1),C(-4,-m)三点在同一条直线上,试确定常数m的值.
【解题提示】 因为点A,B,C的横坐标不是都相同,所以三点所在直线不会垂直于x轴,即斜率存在.
【思路点拨】 如果A,B,C三点在同一条直线上,则直线AB的斜率与直线BC的斜率相等.
【解】 因为A,B,C三点所在直线不可能垂直于x轴,所以设直线AB,BC的斜率分别为kAB,kBC.由斜率公式,得kAB==,kBC==.
因为A,B,C三点在同一条直线上,所以kAB=kBC.
所以= ,即m2-3m-12=0,解得m=或m= .
[2019·广东江门高二期末]已知A(1,2),B(-3,-4),C(2,m),若A,B,C三点共线,则m= ( )
A. B.3 C. D.4
【变式训练】
解析:∵ A,B,C三点共线,∴ kAC=kBC,∴=,解得m=.
答案:C
【解题技法】
已知三点坐标,证明其共线的三种方法
1.从直线的倾斜角、斜率角度,证明三点共线;
2.从直线的方向向量角度,证明三点共线:若证点A,B,C共线,只要证明任意两点组成的两个向量共线即可.
3.若证点A,B,C共线,只要证明|AB|+|AC|=|BC|(或|AB|+|BC|=|AC|或|AC|+|BC|=|AB|)即可.
题组四 直线的方向向量
<1>已知两点的坐标,求其所在直线的方向向量/已知直线的方向向量,求其倾斜角、斜率
例16 已知直线l经过点A(0,1)和B(1,1-),求直线l的一个方向向量,并确定直线l的斜率和倾斜角.
【解】 由已知可得=(1,1- )-(0,1)=(1,- )是直线l的一个方向向量.因此直线l的斜率k= =- .
直线的倾斜角θ满足tan θ=- ,从而可知θ=120°.
已知直线l经过点A(-2,0)和B(-5,3),求直线l的一个方向向量,并确定直线l的斜率和倾斜角.
【变式训练】
解:由已知可得 =(-5,3)-(-2,0)=(-3,3)是直线l的一个方向向量.
因此直线l的斜率k==-1.
直线l的倾斜角θ满足tan θ=-1,从而可知θ=135°.
<2>从直线的方向向量角度,证明三点共线
例17 求证:A(1,5),B(0,2),C(2,8)三点共线.
【证明】 (方法1)利用斜率公式计算出AB和AC两条直线的斜率,
kAB==3,kAC==3.
因为直线AB和AC的斜率相同,又直线AB和AC过同一点A,
所以A,B,C三点共线.
(方法2)因为 =(0-1,2-5)=(-1,-3), =(2-1,8-5)=(1,3),又因为(-1)×3=(-3)×1,所以和共线.又和有公共点A,
所以A,B,C三点共线.
(方法3)因为|AB|==,
|AC|== ,|BC|= = ,
即|AB|+|AC|=|BC|,所以A,B,C三点共线.
题组五 直线的法向量
例18 已知直线l的一个法向量为v=(3,-3),求直线l的一个方向向量,斜率和倾斜角.
【解】 由题易知,直线l的一个方向向量为a=(3,3),所以直线l的斜率为kl=1,倾斜角为45°.
题组六 巧用直线的斜率公式解题
例19 [2019·宁夏银川高一检测]已知实数x,y满足y=x2-2x+2(-1≤x≤1),试求的最大值和最小值.
【解题提示】 的最大值和最小值可以看做过两点(-2,-3)和(x,y)的直线的斜率的最大值和最小值.
【解】 如图,由的几何意义可知它表示经过定点P(-2,-3)与曲线段AB上任一点(x,y)的直线的斜率k,由图可知kPA≤k≤kPB,由已知可得A(1,1),B(-1,5).
则kPA= =,kPB= =8.
∴ ≤k≤8,∴ 的最大值为8,最小值为 .
[2019·河南洛阳一中高一月考]已知实数x,y满足y=-2x+8,且2≤x≤3,求的最大值和最小值.
【变式训练】
解:如图所示,由于实数x,y满足关系式y=-2x+8,且
2≤x≤3,可知点P(x,y)在线段AB上移动,并且A,B两点的坐标可分别求得为(2,4),(3,2).
由于的几何意义是直线OP的斜率,且kOA=2,kOB=,
所以可求得的最大值为2,最小值为.
小结
1.直线的倾斜角与斜率
倾斜角的取值范围是 [0°,180°)(即[0,π))
若A(x1,y1),B(x2,y2)是直线l上两个不同的点,则当x1≠x2时,直
线l的斜率为k=,当x1=x2时,直线l的斜率不存在.
1.直线的倾斜角与斜率
2.直线的方向向量
一般地,如果已知a=(u,v)为直线l的一个方向向量,则:
(1)当u=0时,显然直线l的斜率不存在,倾斜角为90°;
(2)当u≠0时,直线l的斜率是存在的,而且此时(1,k)与a=(u,v)都是直线l的一个方向向量,由直线的任意两个方向向量共线可知1×v=k×u,从而k=,因此可知倾斜角满足tan θ= .
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJ·B-选择性必修第一册
2.2 直线及其方程
2.2.1 直线的倾斜角与斜率
第二章 平面解析几何
重点:理解直线的斜率的概念,探索如何通过直线上两点求直线的斜率
难点:理解斜率的几何意义及其与“相似比”等概念之间的内在联系
1.理解直线的倾斜角和斜率的概念.
2.理解直线斜率的几何意义;掌握倾斜角与斜率的对应关系.
3.掌握过两点的直线的斜率公式.
学习目标
知识梳理
1.直线的倾斜角与斜率
一般地,给定平面直角坐标系中的一条直线,如果这条直线与x轴相交,将x轴绕着它们的交点按逆时针方向旋转到与直线重合时所转的最小正角记为θ,则称θ为这条直线的倾斜角.
倾斜角的取值范围是 (即 ).
特别地,与x轴平行或重合(即与y轴垂直)的直线,倾斜角为 ,与x轴垂直的直线,倾斜角为 .
[0°,180°)
[0,π)
0°
90°
一般地,如果直线l的倾斜角为θ,则当θ≠90°时,称k=tan θ为直线l的斜率;当θ=90°时,称直线l的斜率不存在.
若A(x1,y1),B(x2,y2)是直线l上两个不同的点,则当x1≠x2时,直
线l的斜率为k= ,当x1=x2时,直线l的斜率不存在.
2.直线的方向向量
一般地,如图(1)(2)所示,当θ为直线l的倾斜角时,如果 是直线l的一个方向向量,而且| |=1,则根据三角函数的定义可知点P的坐标为
(cos θ,sin θ).这就是说,此时=(cos θ,sin θ)一定是直线l的一个方向向量.
(1) (2)
当然,此时对于任意的实数λ≠0,=(λcos θ,λsin θ)也是直线l的一
个方向向量.当θ≠90°时,直线的斜率k是存在的,而且k=tan θ= ,
因此,此时如果令λ=,则可知(1,k)也一定是直线l的一个方向向量.
一般地,如果已知a=(u,v)为直线l的一个方向向量,则:
(1)当u=0时,显然直线l的斜率不存在,倾斜角为90°;
(2)当u≠0时,直线l的斜率是存在的,而且此时(1,k)与a=(u,v)都是直线l的一个方向向量,由直线的任意两个方向向量共线可知1×v=k×u,从而k=,因此可知倾斜角满足tan θ= .
直线l的方向向量不唯一,直线l的所有方向向量共线.
3.直线的法向量
一般地,如果表示非零向量v的有向线段所在直线与直线l垂直,则称向量v为直线l的一个法向量,记作v⊥l.
一条直线的方向向量与法向量 .
特别地,当x0与y0不全为0时,因为向量(x0,y0)与(y0,-x0)是互相垂直的,所以,如果其中一个为直线l的一个方向向量,则另一个一定是直线l的一个法向量.
常考题型
题组一 直线的倾斜角
<1>识别直线的倾斜角
例1 图中直线的倾斜角标注正确的有 个.
(1) (2) (3) (4)
【解析】 对于(1),角α的一边取的是x轴的负方向,因此标注不正确;对于(2),角α的一边取的是直线向下的方向,因此标注不正确;对于(3),角α的两边分别取的是x轴的负方向和直线向下的方向,因此标注不正确;对于(4),角α是y轴正方向与直线向上方向所成的角,因此标注不正确.故标注正确的有0个.
【答案】 0
<2>用直线倾斜角的定义,直接求直线的倾斜角
例2 求出图中各直线的倾斜角.
(1) (2) (3)
【解】(1)如图(1),可知∠OAB为直线l1的倾斜角,易知∠ABO=30°,
∴ ∠OAB=60°,即直线l1的倾斜角为60°.
(2)如图2-2-3(2),可知∠xAB为直线l2的倾斜角,易知∠OBA=45°,
∴ ∠OAB=45°,∴ ∠xAB=135°,即直线l2的倾斜角为135°.
(3)如图(3),可知∠OAC为直线l3的倾斜角,易知∠ABO=60°,∴ ∠BAO=30°,∴ ∠OAC=150°,即直线l3的倾斜角为150°.
(1) (2) (3)
【变式训练】
设直线l过原点,其倾斜角为α,将直线l绕坐标原点按逆时针方向旋转30°,得到直线l1,则直线l1的倾斜角为 ( )
A.α+30°
B.α-150°
C.150°-α
D.当0°≤α<150°时为α+30°,当150°≤α<180°时为α-150°
<3>已知两点坐标,求其所在直线的倾斜角
例3 已知a,b,c是三个互不相等的实数,求经过下列两点的直线的倾斜角.
(1)A(a,c),B(b,c);(2)C(a,b),D(a,c);
(3)P(b,b+c),Q(a,c+a).
【解】 (1)因为点A,B的纵坐标相等均为c,所以直线AB的倾斜角为0°.
(2)因为点C,D的横坐标相等均为a,所以直线CD的倾斜角为90°.
(3)设直线PQ的倾斜角为θ,则tan θ==1,所以直线PQ的倾斜角为45°.
【变式训练】
已知坐标平面内三点A(-1,1),B(1,1),C(2,+1).求直线AB,BC,AC的倾斜角.
解:设直线AB,BC,AC的倾斜角分别为θ1,θ2,θ3,
则tan θ1==0,tan θ2= =,tan θ3= =.
∵ 倾斜角的取值范围是[0°,180°),
又∵ tan 0°=0,tan 60°= ,tan 30°= ,
∴ AB的倾斜角θ1=0°,BC的倾斜角θ2=60°,AC的倾斜角θ3=30°.
解题方法:
已知不同两点A(x1,y1),B(x2,y2),求这两点所在直线的倾斜角α的取值范围时,要注意分别考虑四种情况:
(1)当x1=x2时,α=90°;
(2)当y1=y2时,α=0°;
(3)当tan α=>0时,α∈(0°,90°);
(4)当tan α= <0时,α∈(90°,180°).
<4>已知两点含参坐标,在其所在直线倾斜角大小限制条件下,求参数
例4 已知M(2m+3,m),N(m-2,1),
(1)当m为何值时,直线MN的倾斜角为锐角?
(2)当m为何值时,直线MN的倾斜角为钝角?
(3)当m为何值时,直线MN的倾斜角为直角?
【解】 (1)因为点A,B的纵坐标相等均为c,所以直线AB的倾斜角为0°.
(2)因为点C,D的横坐标相等均为a,所以直线CD的倾斜角为90°.
(3)设直线PQ的倾斜角为θ,则tan θ==1,所以直线PQ的倾斜角为45°.
【解】 设直线MN的倾斜角为θ,
(1)直线MN的倾斜角为锐角?tan θ>0,即>0,解得m>1或m<-5.
(2)直线MN的倾斜角为钝角?tan θ<0,即<0,解得-5
已知直线l经过点A(1,t)和B(-2,1),试问,当t取何值时,直线l的倾斜角α为(1)45°;(2)60°;(3)120°?
【变式训练】
解:(1)因为直线l的倾斜角α=45°,且tan 45°=1,
所以tan α=tan 45°===1,解得t=4.
(2)因为直线l的倾斜角α=60°,且tan 60°=,所以tan α=tan 60°= == ,解得t= +1.
已知直线l经过点A(1,t)和B(-2,1),试问,当t取何值时,直线l的倾斜角α为(1)45°;(2)60°;(3)120°?
【变式训练】
(3)因为直线l的倾斜角α=120°,且tan 120°=- ,
所以tan α=tan 120°= ==- ,
解得t=1- .
<5>已知一点坐标,在限定范围内,求其所在直线倾斜角的取值范围
例5 [2020·福建三明高一段考]已知两点A(-4,+1),B(3,2),过点P(2,1)的直线l与线段AB有公共点,求直线l的倾斜角α的取值范围.
【解】 如图所示,过点P,A作直线PA,过点P,B作直线PB.
∵ =,=1,
∴ 直线PA的倾斜角为α1=150°,直线PB的倾斜角为α2=45°.
∵ 直线l与线段AB有公共点,
∴ 由图形易得直线l的倾斜角α的取值范围为45°≤α≤150°.
已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点,求l的倾斜角α的取值范围.
【变式训练】
解:设直线PA的倾斜角为θ1,直线PB的倾斜角为θ2,如图,
∵ tan θ1==-1,tan θ2==1,
∴ PA的倾斜角θ1=135°,PB的倾斜角θ2=45°.
又直线l的倾斜角介于直线PB与PA的倾斜角之间,
∴ 直线l的倾斜角α的取值范围是45°≤α≤135°.
<6>已知两点含参坐标,求其所在直线倾斜角的取值范围
例6 求经过A(m,3),B(1,2)两点的直线的倾斜角α的取值范围.
【解】 当m=1时,直线AB的倾斜角α=90°;
当m>1时,因为>0,所以直线AB的倾斜角α的取值范围是0°<α<90°;
当m<1时,因为<0,所以直线AB的倾斜角α的取值范围是90°<α<180°.
综上,当m=1时,α=90°;
当m>1时,0°<α<90°;当m<1时,90°<α<180°.
[2020·河南项城高一检测]已知两点A(-1,2),B(m,3),实数m∈,求直线AB的倾斜角α的取值范围.
【变式训练】
解:当m=-1时,α=90°;
当m∈ 时,tan α=∈(-∞,-],此时α∈(90°,120°];
当m∈(-1, -1]时,tan α= ∈ ,此时α∈[30°,90°).
综上所述,倾斜角α的取值范围为[30°,120°].
题组二 直线的斜率
<1>已知直线的斜率,求其倾斜角
例7 已知直线l的斜率为-1,则它的倾斜角为 .
【解析】 设直线l的倾斜角为α,0°≤α<180°,则tan α=-1,所以α=135°.
【答案】 135°
<2>已知两点含参坐标,在其所在直线的斜率大小限制条件下,求参数
例8 已知一条直线经过点A(-a,6),B(1,3a),且斜率为12,求a的值.
【解】 由题意得=12,即3a-6=12+12a(a≠-1),解得a=-2.
【注意】 已知直线的斜率为12,因此不用考虑-a=1(即x1=x2)的情况.
已知经过两点A(5,m)和B(m,8)的直线的斜率大于1,求实数m的取值范围.
【变式训练】
解:由题意得>1,∴ -1>0,
∴ >0,即<0,∴ 5
例9 若直线AB与y轴的夹角为60°,则直线AB的倾斜角为 ,斜率为 .
解析:不妨设直线AB过原点,如图,直线AB的倾斜角为30°或150°,其斜率为 或- .
答案: 30°或150° 或-
[2020·江苏南京高二检测]已知直线AB的斜率为-,直线l的倾斜角是直线AB的倾斜角的一半,求直线l的斜率.
【变式训练】
解:∵ 直线AB的斜率kAB=- ,∴ 直线AB的倾斜角是120°,∴ 直线l的倾斜角是60°,∴ 直线l的斜率k=tan 60°= .
<4>已知两点坐标,求其所在直线的斜率
例10 经过下列两点的直线的斜率k是否存在?若存在,求其斜率;若不存在,说明理由.
(1)(1,-1),(-3,2);(2)(1,-2),(5,-2);
(3)(3,4),(-2,-5);(4)(3,0),(3,).
【解】 (1)存在.k==-.(2)存在.k= =0.
(3)存在.k= =.(4)不存在.理由:∵ x1=x2,∴ k不存在.
如图所示,直线l1,l2,l3都经过点P(3,2),又l1,l2,l3分别经过点Q1(-2,-1),Q2(4,-2),Q3(-3,2),计算直线l1,l2,l3的斜率,并判断这些直线的倾斜角是锐角还是钝角.
【变式训练】
解:设k1,k2,k3分别表示直线l1,l2,l3的斜率.
因为Q1,Q2,Q3的横坐标与P点的横坐标均不相等,
所以k1==,k2= =-4,k3= =0.
由k1>0知直线l1的倾斜角为锐角;
由k2<0知直线l2的倾斜角为钝角;
由k3=0知直线l3的倾斜角为0°,既不是锐角也不是钝角.
<5>已知两点含参坐标,求其所在直线的斜率
例11 [2019·甘肃武威高一检测]求过下列两点的直线的斜率k.
(1)A(a,b),B(ma,mb)(m≠1,a≠0);
(2)P(2,1),Q(m,2).
【解题提示】 已知直线上两点A(x1,y1),B(x2,y2),当x1≠x2时,k= ;当x1=x2时,k不存在.
【解】 (1)∵ m≠1,a≠0,∴ k== .
(2)当m=2时,直线与x轴垂直,斜率k不存在;当m≠2时,k==.
经过下列两点的直线的斜率是否存在?若存在,求其斜率;若不存在,说明理由.
(1)A(3,2),B(5,-6);
(2)E(2,-3),F(m,-2)(m∈R).
【变式训练】
解:(1)因为3≠5,所以直线的斜率存在,kAB==-4.
(2)当m=2时,直线的斜率不存在;当m≠2时,直线的斜率存在,且kEF==.
<6>已知直线的倾斜角大小,判断其斜率的大小
例12 如图,已知直线l1,l2,l3的斜率分别为k1,k2,k3,则k1,k2,k3之间的大小关系为 (按从大到小的顺序排列).
【解题提示】 根据直线的倾斜程度判断倾斜角
是锐角还是钝角,进而比较斜率的大小.
【解析】 由图可知直线l1的倾斜角为钝角,所以k1<0;直线l2与直线l3的倾斜角均为锐角,且直线l2的倾斜角较大,所以k2>k3>0,所以k2>k3>k1.
【答案】 k2>k3>k1
如图所示,设k1,k2,k3分别为直线l1,l2,l3的斜率,则k1,k2,k3的大小关系
是 .
【变式训练】
解析:设直线l1,l2,l3的倾斜角分别为α1,α2,α3,
则由题图可知0°<α1<90°<α3<α2<180°,因此k3
例13 [2019·天津高一检测]已知坐标平面内三点A(-1,1),B(1,1),C(2,+1).
(1)求直线AB,BC,AC的斜率.
(2)若D为△ABC的边AB上一动点,求直线CD的斜率k的取值范围.
【解题提示】 (1)利用k=(x1≠x2)求解;
(2)先求出AC,BC的斜率,进而求出k的范围.
【解】 (1)由斜率公式得kAB==0,kBC= =,
kAC= =.
(2)如图,当直线CD由CA逆时针方向旋转到CB时,直线CD与AB恒有交点,即D在线段AB上,此时k由kCA增大到kCB,所以k的取值范围为 .
[2020·浙江嘉兴一中高二检测]过点P(-1,2)的直线l与线段AB相交,且A(-2,-3),B(3,0),求直线l的斜率k的取值范围.
【变式训练】
解:如图,kPA==5,kPB== .取C点为(-1,0).
过点P且与x轴垂直的直线PC与线段AB相交,但此时直线l的斜率不存在.在直线l由PA绕P点逆时针旋转到PC(不包括PC)处的过程中,l的斜率始终为正,且逐渐增大,此时直线l的斜率k的范围是[5,+∞).在直线l由PC(不包括PC)绕P点逆时针旋转到PB处的过程中,斜率为负且逐渐变大,此时l的斜率k的范围是.
故直线l的斜率k的取值范围是∪[5,+∞).
题组三 从直线的倾斜角、斜率角度,解决三点共线问题
<1>从直线的倾斜角、斜率角度,证明三点共线
例14 求证:三点A(-2,3),B(7,6),C(4,5)在同一直线上.
【解题提示】 (1)因为一个定点和斜率就可确定一条直线,所以要证这三点共线,只需证任意两点所连直线的斜率相等即可.
(2)当直线的斜率存在时,A,B,C三点共线等价于kAB=kAC或kAB=kBC或kAC=kBC.
【证明】 ∵ A(-2,3),B(7,6),C(4,5),
∴ kAB== ,kAC= =.∴ kAB=kAC.
又直线AB、直线AC均过点A,∴ 直线AB,AC重合,即A,B,C三点共线.
求证:A(1,-1),B(-2,-7),C(0,-3)三点共线.
【变式训练】
解:∵ A(1,-1),B(-2,-7),C(0,-3),
∴ kAB==2,kAC= =2,则kAB=kAC.
∵ 直线AB与直线AC过同一点A且斜率相同,
∴ 直线AB与直线AC为同一条直线,
故A,B,C三点共线.
<2>从直线的倾斜角、斜率角度,已知三点共线,求参数
例15 如果,B(4,-1),C(-4,-m)三点在同一条直线上,试确定常数m的值.
【解题提示】 因为点A,B,C的横坐标不是都相同,所以三点所在直线不会垂直于x轴,即斜率存在.
【思路点拨】 如果A,B,C三点在同一条直线上,则直线AB的斜率与直线BC的斜率相等.
【解】 因为A,B,C三点所在直线不可能垂直于x轴,所以设直线AB,BC的斜率分别为kAB,kBC.由斜率公式,得kAB==,kBC==.
因为A,B,C三点在同一条直线上,所以kAB=kBC.
所以= ,即m2-3m-12=0,解得m=或m= .
[2019·广东江门高二期末]已知A(1,2),B(-3,-4),C(2,m),若A,B,C三点共线,则m= ( )
A. B.3 C. D.4
【变式训练】
解析:∵ A,B,C三点共线,∴ kAC=kBC,∴=,解得m=.
答案:C
【解题技法】
已知三点坐标,证明其共线的三种方法
1.从直线的倾斜角、斜率角度,证明三点共线;
2.从直线的方向向量角度,证明三点共线:若证点A,B,C共线,只要证明任意两点组成的两个向量共线即可.
3.若证点A,B,C共线,只要证明|AB|+|AC|=|BC|(或|AB|+|BC|=|AC|或|AC|+|BC|=|AB|)即可.
题组四 直线的方向向量
<1>已知两点的坐标,求其所在直线的方向向量/已知直线的方向向量,求其倾斜角、斜率
例16 已知直线l经过点A(0,1)和B(1,1-),求直线l的一个方向向量,并确定直线l的斜率和倾斜角.
【解】 由已知可得=(1,1- )-(0,1)=(1,- )是直线l的一个方向向量.因此直线l的斜率k= =- .
直线的倾斜角θ满足tan θ=- ,从而可知θ=120°.
已知直线l经过点A(-2,0)和B(-5,3),求直线l的一个方向向量,并确定直线l的斜率和倾斜角.
【变式训练】
解:由已知可得 =(-5,3)-(-2,0)=(-3,3)是直线l的一个方向向量.
因此直线l的斜率k==-1.
直线l的倾斜角θ满足tan θ=-1,从而可知θ=135°.
<2>从直线的方向向量角度,证明三点共线
例17 求证:A(1,5),B(0,2),C(2,8)三点共线.
【证明】 (方法1)利用斜率公式计算出AB和AC两条直线的斜率,
kAB==3,kAC==3.
因为直线AB和AC的斜率相同,又直线AB和AC过同一点A,
所以A,B,C三点共线.
(方法2)因为 =(0-1,2-5)=(-1,-3), =(2-1,8-5)=(1,3),又因为(-1)×3=(-3)×1,所以和共线.又和有公共点A,
所以A,B,C三点共线.
(方法3)因为|AB|==,
|AC|== ,|BC|= = ,
即|AB|+|AC|=|BC|,所以A,B,C三点共线.
题组五 直线的法向量
例18 已知直线l的一个法向量为v=(3,-3),求直线l的一个方向向量,斜率和倾斜角.
【解】 由题易知,直线l的一个方向向量为a=(3,3),所以直线l的斜率为kl=1,倾斜角为45°.
题组六 巧用直线的斜率公式解题
例19 [2019·宁夏银川高一检测]已知实数x,y满足y=x2-2x+2(-1≤x≤1),试求的最大值和最小值.
【解题提示】 的最大值和最小值可以看做过两点(-2,-3)和(x,y)的直线的斜率的最大值和最小值.
【解】 如图,由的几何意义可知它表示经过定点P(-2,-3)与曲线段AB上任一点(x,y)的直线的斜率k,由图可知kPA≤k≤kPB,由已知可得A(1,1),B(-1,5).
则kPA= =,kPB= =8.
∴ ≤k≤8,∴ 的最大值为8,最小值为 .
[2019·河南洛阳一中高一月考]已知实数x,y满足y=-2x+8,且2≤x≤3,求的最大值和最小值.
【变式训练】
解:如图所示,由于实数x,y满足关系式y=-2x+8,且
2≤x≤3,可知点P(x,y)在线段AB上移动,并且A,B两点的坐标可分别求得为(2,4),(3,2).
由于的几何意义是直线OP的斜率,且kOA=2,kOB=,
所以可求得的最大值为2,最小值为.
小结
1.直线的倾斜角与斜率
倾斜角的取值范围是 [0°,180°)(即[0,π))
若A(x1,y1),B(x2,y2)是直线l上两个不同的点,则当x1≠x2时,直
线l的斜率为k=,当x1=x2时,直线l的斜率不存在.
1.直线的倾斜角与斜率
2.直线的方向向量
一般地,如果已知a=(u,v)为直线l的一个方向向量,则:
(1)当u=0时,显然直线l的斜率不存在,倾斜角为90°;
(2)当u≠0时,直线l的斜率是存在的,而且此时(1,k)与a=(u,v)都是直线l的一个方向向量,由直线的任意两个方向向量共线可知1×v=k×u,从而k=,因此可知倾斜角满足tan θ= .
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
