15.1.4多项式乘以多项式
文档属性
| 名称 | 15.1.4多项式乘以多项式 |  | |
| 格式 | zip | ||
| 文件大小 | 108.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-25 22:46:24 | ||
图片预览



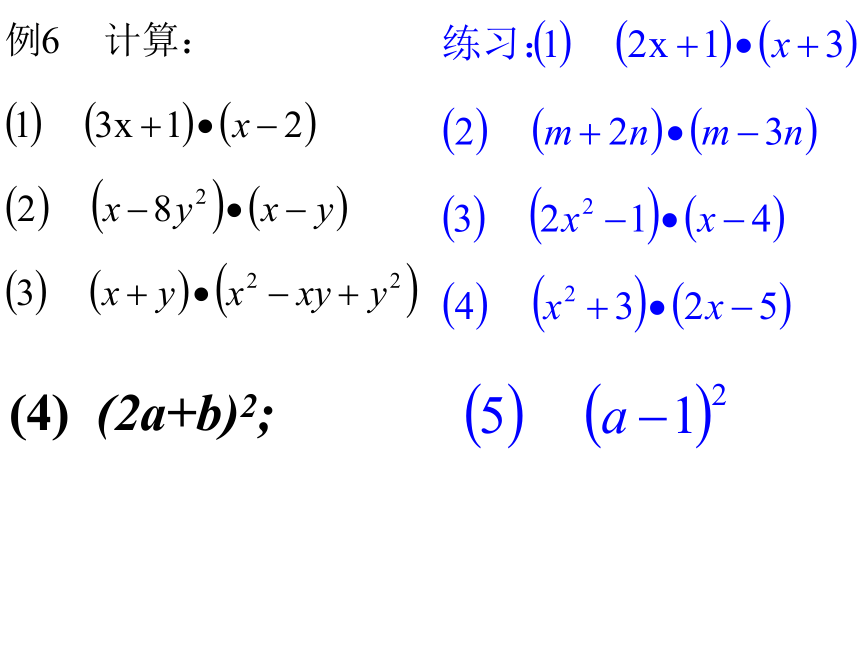

文档简介
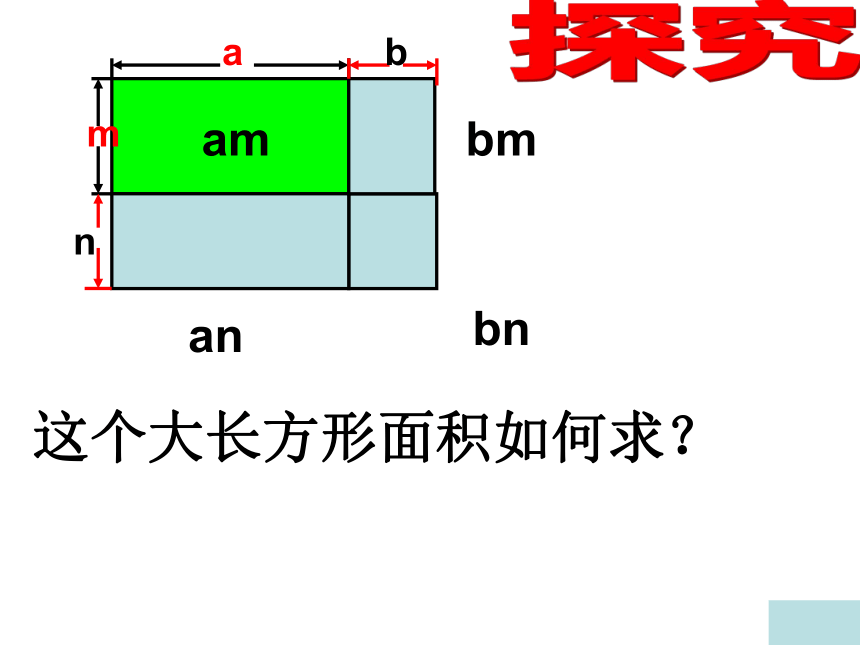
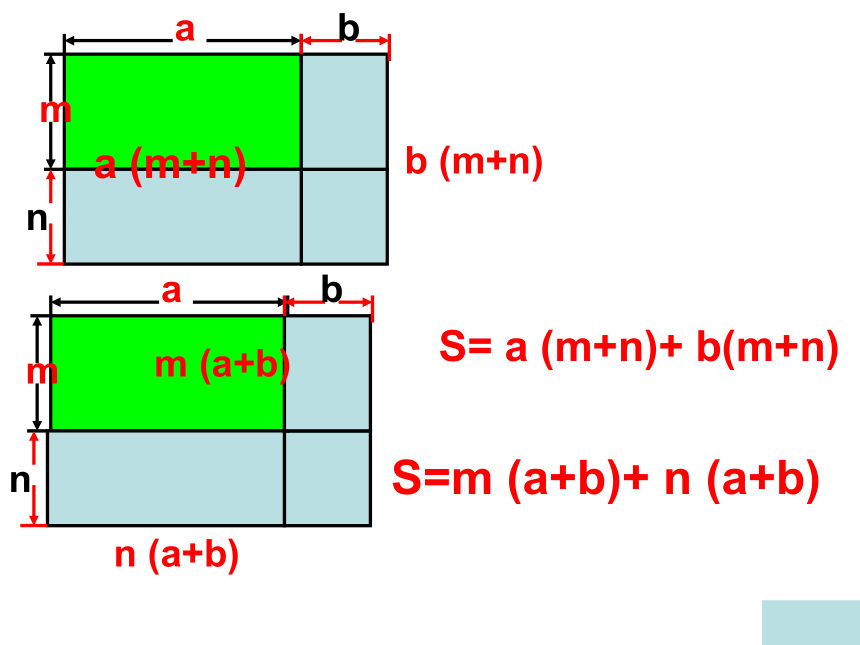
课件15张PPT。多项式乘以多项式 单项式与多项式相乘 -3x2y3(x2-1)-(x2+1)?3x2y3amanbnbm探究这个大长方形面积如何求?a (m+n)b (m+n)m (a+b)n (a+b)S= a (m+n)+ b(m+n)
S=m (a+b)+ n (a+b)
(a+b)(m+n)=am多项式的乘法+an+bm+bn 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.(4) (2a+b)2; (x+2)(x+3) =
(x-4)(x+1) =
(y+4)(y-2) =
(y-5)(y-3) = 观察上述式子,你可以得出一个什么规律吗? (x+p)(x+q) =? (x+2)(x+3) = x2 + 5x+6;
(x-4)(x+1) = x2 – 3x-4
(y+4)(y-2) = y2 + 2y-8
(y-5)(y-3). = y2- 8y+15
观察上述式子,你可以 得出一个什么规律吗? (x+p)(x+q) = x2 + (p+q) x + p q练习:确定下列各式中m的值:
(1) (x+4)(x+9) = x2 + m x + 36
(2) (x-2)(x-18) = x + m x + 36
(3) (x+3)(x+p) = x + m x + 36
(4) (x-6) (x-p) = x + m x + 36
(5) (x+p)(x+q) = x + m x + 36
(p,q为正整数) m =13 m = - 20 p =12, m= 15 p= -6, m= -12 p = 4,q = 9, m =13 p=2,q = 18, m=20 p = 3, q =12, m=15 p=6, q= 6, m=12解方程与不等式:
(1) (x-3)(x-2)+18 = (x+9)(x+1);
(2) (3x+4)(3x-4) <9(x-2)(x+3).
解:原式 小 结1、多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.2、多项式与多项式相乘时,多项式的每一项都应该带上它前面的正负号。多项式是单项式的和,每一项都包括前面的符号,在计算时一定要注意确定各项的符号。4、在数学知识的学习中,“转化”思想是的重要思想方法。在今天的学习中,第一步是“转化”为多项式与单项式相乘,第二步是“转化”为单项式乘法。即将新的知识、方法化为已知的数学知识、方法。从而使学习能够进行。 3、(x+p)(x+q) = x2 + (p+q) x + p q练习:(1) (xy–z)(2xy+z) ;(2) (x–1)(x2+x+1) ;(3) (2a+b)2;(4) (3a–2)(a–1)–(a+1)(a+2) ;课件15张PPT。多项式乘以多项式 单项式与多项式相乘 -3x2y3(x2-1)-(x2+1)?3x2y3amanbnbm探究这个大长方形面积如何求?a (m+n)b (m+n)m (a+b)n (a+b)S= a (m+n)+ b(m+n)
S=m (a+b)+ n (a+b)
(a+b)(m+n)=am多项式的乘法+an+bm+bn 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.(4) (2a+b)2; (x+2)(x+3) =
(x-4)(x+1) =
(y+4)(y-2) =
(y-5)(y-3) = 观察上述式子,你可以得出一个什么规律吗? (x+p)(x+q) =? (x+2)(x+3) = x2 + 5x+6;
(x-4)(x+1) = x2 – 3x-4
(y+4)(y-2) = y2 + 2y-8
(y-5)(y-3). = y2- 8y+15
观察上述式子,你可以 得出一个什么规律吗? (x+p)(x+q) = x2 + (p+q) x + p q练习:确定下列各式中m的值:
(1) (x+4)(x+9) = x2 + m x + 36
(2) (x-2)(x-18) = x + m x + 36
(3) (x+3)(x+p) = x + m x + 36
(4) (x-6) (x-p) = x + m x + 36
(5) (x+p)(x+q) = x + m x + 36
(p,q为正整数) m =13 m = - 20 p =12, m= 15 p= -6, m= -12 p = 4,q = 9, m =13 p=2,q = 18, m=20 p = 3, q =12, m=15 p=6, q= 6, m=12解方程与不等式:
(1) (x-3)(x-2)+18 = (x+9)(x+1);
(2) (3x+4)(3x-4) <9(x-2)(x+3).
例2 先化简,再求值:(2a-3)(3a+1)-6a(a-4)
其中a=解:原式 小 结1、多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.2、多项式与多项式相乘时,多项式的每一项都应该带上它前面的正负号。多项式是单项式的和,每一项都包括前面的符号,在计算时一定要注意确定各项的符号。4、在数学知识的学习中,“转化”思想是的重要思想方法。在今天的学习中,第一步是“转化”为多项式与单项式相乘,第二步是“转化”为单项式乘法。即将新的知识、方法化为已知的数学知识、方法。从而使学习能够进行。 3、(x+p)(x+q) = x2 + (p+q) x + p q练习:(1) (xy–z)(2xy+z) ;(2) (x–1)(x2+x+1) ;(3) (2a+b)2;(4) (3a–2)(a–1)–(a+1)(a+2) ;
S=m (a+b)+ n (a+b)
(a+b)(m+n)=am多项式的乘法+an+bm+bn 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.(4) (2a+b)2; (x+2)(x+3) =
(x-4)(x+1) =
(y+4)(y-2) =
(y-5)(y-3) = 观察上述式子,你可以得出一个什么规律吗? (x+p)(x+q) =? (x+2)(x+3) = x2 + 5x+6;
(x-4)(x+1) = x2 – 3x-4
(y+4)(y-2) = y2 + 2y-8
(y-5)(y-3). = y2- 8y+15
观察上述式子,你可以 得出一个什么规律吗? (x+p)(x+q) = x2 + (p+q) x + p q练习:确定下列各式中m的值:
(1) (x+4)(x+9) = x2 + m x + 36
(2) (x-2)(x-18) = x + m x + 36
(3) (x+3)(x+p) = x + m x + 36
(4) (x-6) (x-p) = x + m x + 36
(5) (x+p)(x+q) = x + m x + 36
(p,q为正整数) m =13 m = - 20 p =12, m= 15 p= -6, m= -12 p = 4,q = 9, m =13 p=2,q = 18, m=20 p = 3, q =12, m=15 p=6, q= 6, m=12解方程与不等式:
(1) (x-3)(x-2)+18 = (x+9)(x+1);
(2) (3x+4)(3x-4) <9(x-2)(x+3).
解:原式 小 结1、多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.2、多项式与多项式相乘时,多项式的每一项都应该带上它前面的正负号。多项式是单项式的和,每一项都包括前面的符号,在计算时一定要注意确定各项的符号。4、在数学知识的学习中,“转化”思想是的重要思想方法。在今天的学习中,第一步是“转化”为多项式与单项式相乘,第二步是“转化”为单项式乘法。即将新的知识、方法化为已知的数学知识、方法。从而使学习能够进行。 3、(x+p)(x+q) = x2 + (p+q) x + p q练习:(1) (xy–z)(2xy+z) ;(2) (x–1)(x2+x+1) ;(3) (2a+b)2;(4) (3a–2)(a–1)–(a+1)(a+2) ;课件15张PPT。多项式乘以多项式 单项式与多项式相乘 -3x2y3(x2-1)-(x2+1)?3x2y3amanbnbm探究这个大长方形面积如何求?a (m+n)b (m+n)m (a+b)n (a+b)S= a (m+n)+ b(m+n)
S=m (a+b)+ n (a+b)
(a+b)(m+n)=am多项式的乘法+an+bm+bn 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.(4) (2a+b)2; (x+2)(x+3) =
(x-4)(x+1) =
(y+4)(y-2) =
(y-5)(y-3) = 观察上述式子,你可以得出一个什么规律吗? (x+p)(x+q) =? (x+2)(x+3) = x2 + 5x+6;
(x-4)(x+1) = x2 – 3x-4
(y+4)(y-2) = y2 + 2y-8
(y-5)(y-3). = y2- 8y+15
观察上述式子,你可以 得出一个什么规律吗? (x+p)(x+q) = x2 + (p+q) x + p q练习:确定下列各式中m的值:
(1) (x+4)(x+9) = x2 + m x + 36
(2) (x-2)(x-18) = x + m x + 36
(3) (x+3)(x+p) = x + m x + 36
(4) (x-6) (x-p) = x + m x + 36
(5) (x+p)(x+q) = x + m x + 36
(p,q为正整数) m =13 m = - 20 p =12, m= 15 p= -6, m= -12 p = 4,q = 9, m =13 p=2,q = 18, m=20 p = 3, q =12, m=15 p=6, q= 6, m=12解方程与不等式:
(1) (x-3)(x-2)+18 = (x+9)(x+1);
(2) (3x+4)(3x-4) <9(x-2)(x+3).
例2 先化简,再求值:(2a-3)(3a+1)-6a(a-4)
其中a=解:原式 小 结1、多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.2、多项式与多项式相乘时,多项式的每一项都应该带上它前面的正负号。多项式是单项式的和,每一项都包括前面的符号,在计算时一定要注意确定各项的符号。4、在数学知识的学习中,“转化”思想是的重要思想方法。在今天的学习中,第一步是“转化”为多项式与单项式相乘,第二步是“转化”为单项式乘法。即将新的知识、方法化为已知的数学知识、方法。从而使学习能够进行。 3、(x+p)(x+q) = x2 + (p+q) x + p q练习:(1) (xy–z)(2xy+z) ;(2) (x–1)(x2+x+1) ;(3) (2a+b)2;(4) (3a–2)(a–1)–(a+1)(a+2) ;
