15.2.1平方差公式
图片预览





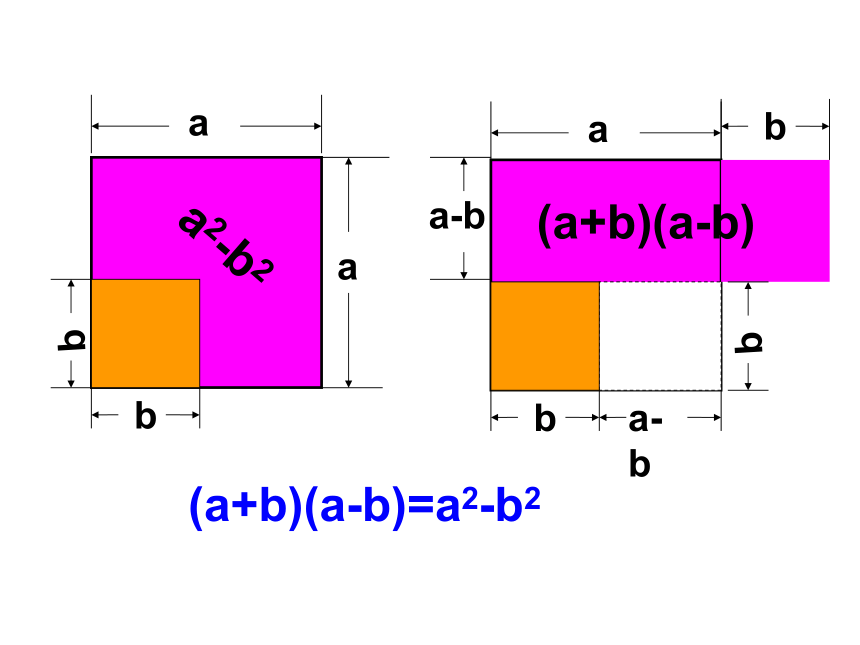

文档简介
(共17张PPT)
15.2.1 平方差公式
200004×199996
=?
计算下列多项式的积,
你能发现什么规律
(x+1)(x-1)=_____;
(m+2)(m-2)=______;
(2x+1)(2x-1)=_____.
x2-1
m2- 4
4x2-1
(a+b)(a-b)=a2-b2
符号相同为a
符号相反为b
(a+b)(a-b) =
a2-b2
即两个数的和与这两个数的差的积,等于这两个数的平方差.
平方差公式:
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
(a+b)(a-b)=a2-b2
a-b
a-b
例1 运用平方差公式计算:
(1) (3x+2) (3x-2);
(a + b) (a -b) = a2 - b2
用公式关键是识别两数
符号相同的项 a
符号相反的项 b
运用平方差公式计算:
(b+2a)(2a-b);
(-x+2y) (-x-2y).
(1) (a+b)( a b) ;
(2) (a b)(b a) ;
(3) (a+2b)(2b+a);
(4) (a b)(a+b) ;
(5) ( 2x+y)(y 2x).
(不能)
下列式子可用平方差公式计算吗 为什么 如果能够,怎样计算
(第一个数不完全一样 )
(不能)
(不能)
(能)
(a2 b2)=
a2 + b2 ;
(不能)
例2 计算:
(1) 102×98;
200004×199996
=(200000+4)(200000-4)
= 2000002 - 42
= 40000000000 - 16
= 39999999984
⑵ (y+2)(y-2)-(y-1)(y+5)
y
y
y
y
2
2
= y2 - 22
1
5
- (y2+4y-5)
= y2-4-y2-4y+5
= -4y+1
ㄨ
下面各式的计算对不对?
如果不对,应当怎样改正?
(1) (x+2)(x-2) = x2 - 2
(2) (-3a-2)(3a-2) = 9a2 - 4
X2 - 4
ㄨ
4 - 9a2
如图1,在边长为a的正方形中挖掉一个边长为b的正方形(a>b),把余下的部分剪成一个矩形(如图2).通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是( )
a2-b2 = (a+b) (a-b)
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
(a+2b)(a-b)=a2+ab-2b2
b
a
图1
b
a
图2
1、[x+(y+1)] [x-(y+1)]
2、(a+b+c) (a+b-c)
3、(x+3) (x-3) (x2+9) (x4+81)
(2+1)(22+1)(24+1)(28+1) … (22n+1)
运用平方差公式计算:
(1+3b) (1-3b)
(4a+3) (4a-3)
(3x+2y2) (3x-2y2)
(x+y+z)(x+y-z)
(b+2a )(2a-b)
(-4a-1)(4a-1)
(3+2a)(-3+2a)
(-0.3x-1)(-0.3x+1)
15.2.1 平方差公式
200004×199996
=?
计算下列多项式的积,
你能发现什么规律
(x+1)(x-1)=_____;
(m+2)(m-2)=______;
(2x+1)(2x-1)=_____.
x2-1
m2- 4
4x2-1
(a+b)(a-b)=a2-b2
符号相同为a
符号相反为b
(a+b)(a-b) =
a2-b2
即两个数的和与这两个数的差的积,等于这两个数的平方差.
平方差公式:
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
(a+b)(a-b)=a2-b2
a-b
a-b
例1 运用平方差公式计算:
(1) (3x+2) (3x-2);
(a + b) (a -b) = a2 - b2
用公式关键是识别两数
符号相同的项 a
符号相反的项 b
运用平方差公式计算:
(b+2a)(2a-b);
(-x+2y) (-x-2y).
(1) (a+b)( a b) ;
(2) (a b)(b a) ;
(3) (a+2b)(2b+a);
(4) (a b)(a+b) ;
(5) ( 2x+y)(y 2x).
(不能)
下列式子可用平方差公式计算吗 为什么 如果能够,怎样计算
(第一个数不完全一样 )
(不能)
(不能)
(能)
(a2 b2)=
a2 + b2 ;
(不能)
例2 计算:
(1) 102×98;
200004×199996
=(200000+4)(200000-4)
= 2000002 - 42
= 40000000000 - 16
= 39999999984
⑵ (y+2)(y-2)-(y-1)(y+5)
y
y
y
y
2
2
= y2 - 22
1
5
- (y2+4y-5)
= y2-4-y2-4y+5
= -4y+1
ㄨ
下面各式的计算对不对?
如果不对,应当怎样改正?
(1) (x+2)(x-2) = x2 - 2
(2) (-3a-2)(3a-2) = 9a2 - 4
X2 - 4
ㄨ
4 - 9a2
如图1,在边长为a的正方形中挖掉一个边长为b的正方形(a>b),把余下的部分剪成一个矩形(如图2).通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是( )
a2-b2 = (a+b) (a-b)
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
(a+2b)(a-b)=a2+ab-2b2
b
a
图1
b
a
图2
1、[x+(y+1)] [x-(y+1)]
2、(a+b+c) (a+b-c)
3、(x+3) (x-3) (x2+9) (x4+81)
(2+1)(22+1)(24+1)(28+1) … (22n+1)
运用平方差公式计算:
(1+3b) (1-3b)
(4a+3) (4a-3)
(3x+2y2) (3x-2y2)
(x+y+z)(x+y-z)
(b+2a )(2a-b)
(-4a-1)(4a-1)
(3+2a)(-3+2a)
(-0.3x-1)(-0.3x+1)
