15.4.1提公因式法
图片预览

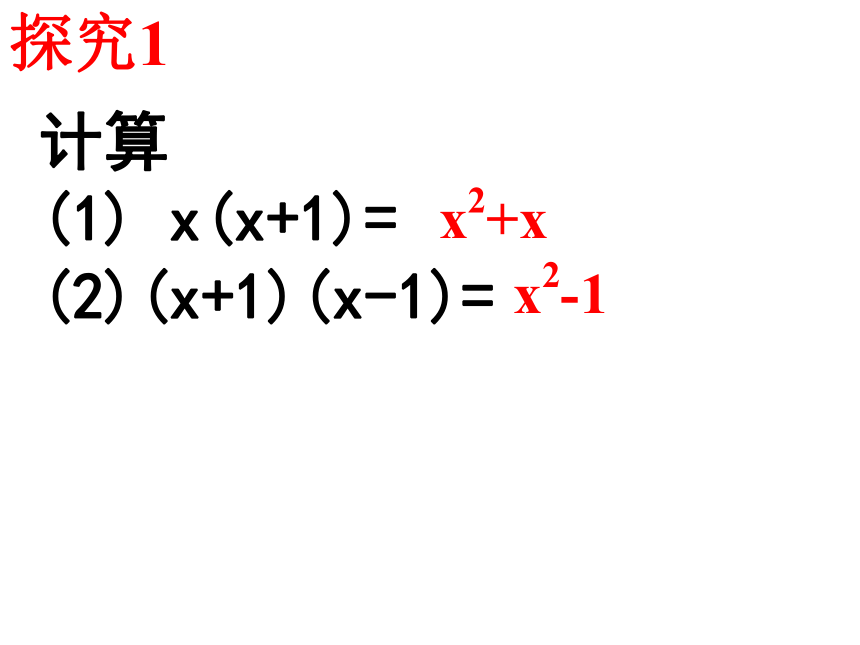




文档简介
课件19张PPT。15.4分解因式
提公因式法探究1计算
(1) x(x+1)=
(2)(x+1)(x-1)= x2+xx2-1也叫因式分解 把一个多项式化成几个整式积的形式,这种变形叫做把这个多项式分解因式.归纳(1) x2+x= x(x+1)
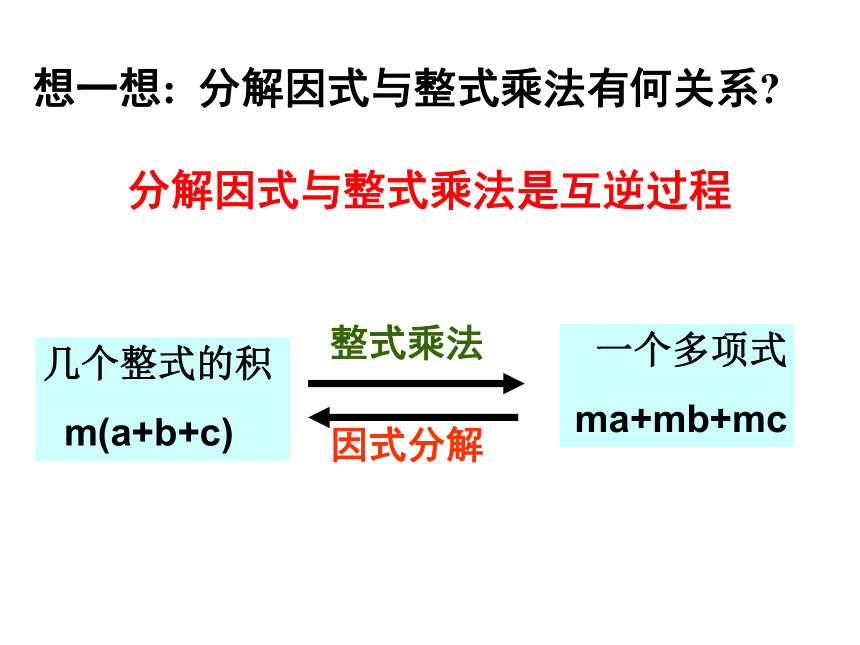
(2) x2-1=(x+1)(x-1)想一想: 分解因式与整式乘法有何关系?分解因式与整式乘法是互逆过程几个整式的积
m(a+b+c)一个多项式
ma+mb+mc 整式乘法因式分解判断下列各式是不是因式分解?(1) x2-4y2 =(x+2y)(x-2y)是不是辨一辨不是(4) m2-3m+1 =m(m-3)+1不是(5) (a-3)(a+3)=a2-9不是下列从左到右的变形是分解因式的有( )⑴ 6x2y=3xy·2x
⑵ a2-b2+1=(a+b)(a-b)+1
⑶ a2-ab=a(a-b)
⑷ (x+3)(x-3)= x2-9
3选择题观察下列多项式2x2+6x3,12a2b3-8a3b2-16ab4各项含有哪些相同的因式?如何确定公因式?公因式=各项系数的最大公约数×
各项都含相同字母的最低次幂
请说出下列多项式的公因式
1、ma + mb
2、4kx - 8ky
3、5y3+20y2
4、a2b-2ab2+ab
5、 4x2-8ax+2x
6、3(a+b)2-6(a+b)3
如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式。这种分解因式的方法叫做提公因式法。提公因式法:提公因式法的一般步骤 :1、确定提取的公因式 2、提取公因式例1、注意:如果多项式的第一项的系数是负的,一般要提出“-”号,练习: 把-4x2+8ax+2x 分解因式
例3 把2a(b-c)-3(b-c)分解因式例4、把2a(b-c)+3(c-b)分解因式。(1) 2a(y-z)-3b(z-y)(2) 6(m-n)3-12(n-m)2练习:把下列各式分解因式:(3) 2(a-b)2 - a+b (4) 2(a-b)2 - (b-a)3 (1) 2x2+3x3+x=x(2x+3x2)
(2) 3a2c-6a3c=3a2(c-2ac)
(3) 3x2+6x-3=3x(x+2)-3
1.下面的因式分解对吗?如果不对,应怎样改正?练一练不对. 2x2+3x3+x=x(2x+3x2+1)不对.3a2c-6a3c=3a2c(1-2a)不对. 3x2+6x-3=3(x2+2x-1)2.利用因式分解进行计算 25×28 - 25×12 - 25×6
32006 - 5×32005 + 6×32004综合拓展
1.(1)分解因式: 1+x+x(1+x)+x(1+x)2+x(1+x)3;
(2)根据(1)中的规律,直接写出多项式1+x+x(1+x)+x(1+x)2+……x(1+x)n-1分解因式的结果.
2.猜一猜:817-279-913能被45整除吗?说明理由.D(2)分解-4x3+8x2+16x的结果是( )
(A)-x(4x2-8x+16) (B)x(-4x2+8x-16)
(C)4(-x3+2x2-4x) (D)-4x(x2-2x-4)(1)多项式6ab2+18a2b2-12a3b2c的公因式( )
(A)6ab2c (B)ab2 (C)6ab2 (D)6a3b2CC1.选择课后练习(3)若多项式-6ab+18abx+24aby的一个因式是-6ab,那么另一 个因式是( )
(A)-1-3x+4y (B)1+3x-4y
(C)-1-3x-4y (D)1-3x-4yD选择题(4)若多项式(a+b)x2+(a+b)x要分解因式,则要提的公因式是 .
(a+b)x3、因式分解:
(1)-6m4n2-3m3n2+15m2n4;
(2)27xn+1-18xn+9xn-1. 小结:
今天我们学习了提取公因式法分解因式,可以用四句顺口溜来总结记忆用提取公因式法分解因式的技巧:各项有“公”先提“公”,
首项有负常提负,
母项提出莫漏1,
括号里面分到“底”。课件19张PPT。15.4分解因式
提公因式法探究1计算
(1) x(x+1)=
(2)(x+1)(x-1)= x2+xx2-1也叫因式分解 把一个多项式化成几个整式积的形式,这种变形叫做把这个多项式分解因式.归纳(1) x2+x= x(x+1)
(2) x2-1=(x+1)(x-1)想一想: 分解因式与整式乘法有何关系?分解因式与整式乘法是互逆过程几个整式的积
m(a+b+c)一个多项式
ma+mb+mc 整式乘法因式分解判断下列各式是不是因式分解?(1) x2-4y2 =(x+2y)(x-2y)是不是辨一辨不是(4) m2-3m+1 =m(m-3)+1不是(3) (5) (a-3)(a+3)=a2-9不是下列从左到右的变形是分解因式的有( )⑴ 6x2y=3xy·2x
⑵ a2-b2+1=(a+b)(a-b)+1
⑶ a2-ab=a(a-b)
⑷ (x+3)(x-3)= x2-9
3选择题观察下列多项式2x2+6x3,12a2b3-8a3b2-16ab4各项含有哪些相同的因式?如何确定公因式?公因式=各项系数的最大公约数×
各项都含相同字母的最低次幂
请说出下列多项式的公因式
1、ma + mb
2、4kx - 8ky
3、5y3+20y2
4、a2b-2ab2+ab
5、 4x2-8ax+2x
6、3(a+b)2-6(a+b)3
如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式。这种分解因式的方法叫做提公因式法。提公因式法:提公因式法的一般步骤 :1、确定提取的公因式 2、提取公因式例1、注意:如果多项式的第一项的系数是负的,一般要提出“-”号,练习: 把-4x2+8ax+2x 分解因式
例3 把2a(b-c)-3(b-c)分解因式例4、把2a(b-c)+3(c-b)分解因式。(1) 2a(y-z)-3b(z-y)(2) 6(m-n)3-12(n-m)2练习:把下列各式分解因式:(3) 2(a-b)2 - a+b (4) 2(a-b)2 - (b-a)3 (1) 2x2+3x3+x=x(2x+3x2)
(2) 3a2c-6a3c=3a2(c-2ac)
(3) 3x2+6x-3=3x(x+2)-3
1.下面的因式分解对吗?如果不对,应怎样改正?练一练不对. 2x2+3x3+x=x(2x+3x2+1)不对.3a2c-6a3c=3a2c(1-2a)不对. 3x2+6x-3=3(x2+2x-1)2.利用因式分解进行计算 25×28 - 25×12 - 25×6
32006 - 5×32005 + 6×32004综合拓展
1.(1)分解因式: 1+x+x(1+x)+x(1+x)2+x(1+x)3;
(2)根据(1)中的规律,直接写出多项式1+x+x(1+x)+x(1+x)2+……x(1+x)n-1分解因式的结果.
2.猜一猜:817-279-913能被45整除吗?说明理由.D(2)分解-4x3+8x2+16x的结果是( )
(A)-x(4x2-8x+16) (B)x(-4x2+8x-16)
(C)4(-x3+2x2-4x) (D)-4x(x2-2x-4)(1)多项式6ab2+18a2b2-12a3b2c的公因式( )
(A)6ab2c (B)ab2 (C)6ab2 (D)6a3b2CC1.选择课后练习(3)若多项式-6ab+18abx+24aby的一个因式是-6ab,那么另一 个因式是( )
(A)-1-3x+4y (B)1+3x-4y
(C)-1-3x-4y (D)1-3x-4yD选择题(4)若多项式(a+b)x2+(a+b)x要分解因式,则要提的公因式是 .
(a+b)x3、因式分解:
(1)-6m4n2-3m3n2+15m2n4;
(2)27xn+1-18xn+9xn-1. 小结:
今天我们学习了提取公因式法分解因式,可以用四句顺口溜来总结记忆用提取公因式法分解因式的技巧:各项有“公”先提“公”,
首项有负常提负,
母项提出莫漏1,
括号里面分到“底”。
提公因式法探究1计算
(1) x(x+1)=
(2)(x+1)(x-1)= x2+xx2-1也叫因式分解 把一个多项式化成几个整式积的形式,这种变形叫做把这个多项式分解因式.归纳(1) x2+x= x(x+1)
(2) x2-1=(x+1)(x-1)想一想: 分解因式与整式乘法有何关系?分解因式与整式乘法是互逆过程几个整式的积
m(a+b+c)一个多项式
ma+mb+mc 整式乘法因式分解判断下列各式是不是因式分解?(1) x2-4y2 =(x+2y)(x-2y)是不是辨一辨不是(4) m2-3m+1 =m(m-3)+1不是(5) (a-3)(a+3)=a2-9不是下列从左到右的变形是分解因式的有( )⑴ 6x2y=3xy·2x
⑵ a2-b2+1=(a+b)(a-b)+1
⑶ a2-ab=a(a-b)
⑷ (x+3)(x-3)= x2-9
3选择题观察下列多项式2x2+6x3,12a2b3-8a3b2-16ab4各项含有哪些相同的因式?如何确定公因式?公因式=各项系数的最大公约数×
各项都含相同字母的最低次幂
请说出下列多项式的公因式
1、ma + mb
2、4kx - 8ky
3、5y3+20y2
4、a2b-2ab2+ab
5、 4x2-8ax+2x
6、3(a+b)2-6(a+b)3
如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式。这种分解因式的方法叫做提公因式法。提公因式法:提公因式法的一般步骤 :1、确定提取的公因式 2、提取公因式例1、注意:如果多项式的第一项的系数是负的,一般要提出“-”号,练习: 把-4x2+8ax+2x 分解因式
例3 把2a(b-c)-3(b-c)分解因式例4、把2a(b-c)+3(c-b)分解因式。(1) 2a(y-z)-3b(z-y)(2) 6(m-n)3-12(n-m)2练习:把下列各式分解因式:(3) 2(a-b)2 - a+b (4) 2(a-b)2 - (b-a)3 (1) 2x2+3x3+x=x(2x+3x2)
(2) 3a2c-6a3c=3a2(c-2ac)
(3) 3x2+6x-3=3x(x+2)-3
1.下面的因式分解对吗?如果不对,应怎样改正?练一练不对. 2x2+3x3+x=x(2x+3x2+1)不对.3a2c-6a3c=3a2c(1-2a)不对. 3x2+6x-3=3(x2+2x-1)2.利用因式分解进行计算 25×28 - 25×12 - 25×6
32006 - 5×32005 + 6×32004综合拓展
1.(1)分解因式: 1+x+x(1+x)+x(1+x)2+x(1+x)3;
(2)根据(1)中的规律,直接写出多项式1+x+x(1+x)+x(1+x)2+……x(1+x)n-1分解因式的结果.
2.猜一猜:817-279-913能被45整除吗?说明理由.D(2)分解-4x3+8x2+16x的结果是( )
(A)-x(4x2-8x+16) (B)x(-4x2+8x-16)
(C)4(-x3+2x2-4x) (D)-4x(x2-2x-4)(1)多项式6ab2+18a2b2-12a3b2c的公因式( )
(A)6ab2c (B)ab2 (C)6ab2 (D)6a3b2CC1.选择课后练习(3)若多项式-6ab+18abx+24aby的一个因式是-6ab,那么另一 个因式是( )
(A)-1-3x+4y (B)1+3x-4y
(C)-1-3x-4y (D)1-3x-4yD选择题(4)若多项式(a+b)x2+(a+b)x要分解因式,则要提的公因式是 .
(a+b)x3、因式分解:
(1)-6m4n2-3m3n2+15m2n4;
(2)27xn+1-18xn+9xn-1. 小结:
今天我们学习了提取公因式法分解因式,可以用四句顺口溜来总结记忆用提取公因式法分解因式的技巧:各项有“公”先提“公”,
首项有负常提负,
母项提出莫漏1,
括号里面分到“底”。课件19张PPT。15.4分解因式
提公因式法探究1计算
(1) x(x+1)=
(2)(x+1)(x-1)= x2+xx2-1也叫因式分解 把一个多项式化成几个整式积的形式,这种变形叫做把这个多项式分解因式.归纳(1) x2+x= x(x+1)
(2) x2-1=(x+1)(x-1)想一想: 分解因式与整式乘法有何关系?分解因式与整式乘法是互逆过程几个整式的积
m(a+b+c)一个多项式
ma+mb+mc 整式乘法因式分解判断下列各式是不是因式分解?(1) x2-4y2 =(x+2y)(x-2y)是不是辨一辨不是(4) m2-3m+1 =m(m-3)+1不是(3) (5) (a-3)(a+3)=a2-9不是下列从左到右的变形是分解因式的有( )⑴ 6x2y=3xy·2x
⑵ a2-b2+1=(a+b)(a-b)+1
⑶ a2-ab=a(a-b)
⑷ (x+3)(x-3)= x2-9
3选择题观察下列多项式2x2+6x3,12a2b3-8a3b2-16ab4各项含有哪些相同的因式?如何确定公因式?公因式=各项系数的最大公约数×
各项都含相同字母的最低次幂
请说出下列多项式的公因式
1、ma + mb
2、4kx - 8ky
3、5y3+20y2
4、a2b-2ab2+ab
5、 4x2-8ax+2x
6、3(a+b)2-6(a+b)3
如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式。这种分解因式的方法叫做提公因式法。提公因式法:提公因式法的一般步骤 :1、确定提取的公因式 2、提取公因式例1、注意:如果多项式的第一项的系数是负的,一般要提出“-”号,练习: 把-4x2+8ax+2x 分解因式
例3 把2a(b-c)-3(b-c)分解因式例4、把2a(b-c)+3(c-b)分解因式。(1) 2a(y-z)-3b(z-y)(2) 6(m-n)3-12(n-m)2练习:把下列各式分解因式:(3) 2(a-b)2 - a+b (4) 2(a-b)2 - (b-a)3 (1) 2x2+3x3+x=x(2x+3x2)
(2) 3a2c-6a3c=3a2(c-2ac)
(3) 3x2+6x-3=3x(x+2)-3
1.下面的因式分解对吗?如果不对,应怎样改正?练一练不对. 2x2+3x3+x=x(2x+3x2+1)不对.3a2c-6a3c=3a2c(1-2a)不对. 3x2+6x-3=3(x2+2x-1)2.利用因式分解进行计算 25×28 - 25×12 - 25×6
32006 - 5×32005 + 6×32004综合拓展
1.(1)分解因式: 1+x+x(1+x)+x(1+x)2+x(1+x)3;
(2)根据(1)中的规律,直接写出多项式1+x+x(1+x)+x(1+x)2+……x(1+x)n-1分解因式的结果.
2.猜一猜:817-279-913能被45整除吗?说明理由.D(2)分解-4x3+8x2+16x的结果是( )
(A)-x(4x2-8x+16) (B)x(-4x2+8x-16)
(C)4(-x3+2x2-4x) (D)-4x(x2-2x-4)(1)多项式6ab2+18a2b2-12a3b2c的公因式( )
(A)6ab2c (B)ab2 (C)6ab2 (D)6a3b2CC1.选择课后练习(3)若多项式-6ab+18abx+24aby的一个因式是-6ab,那么另一 个因式是( )
(A)-1-3x+4y (B)1+3x-4y
(C)-1-3x-4y (D)1-3x-4yD选择题(4)若多项式(a+b)x2+(a+b)x要分解因式,则要提的公因式是 .
(a+b)x3、因式分解:
(1)-6m4n2-3m3n2+15m2n4;
(2)27xn+1-18xn+9xn-1. 小结:
今天我们学习了提取公因式法分解因式,可以用四句顺口溜来总结记忆用提取公因式法分解因式的技巧:各项有“公”先提“公”,
首项有负常提负,
母项提出莫漏1,
括号里面分到“底”。
