15.4.2平方差公式法(1)
文档属性
| 名称 | 15.4.2平方差公式法(1) |

|
|
| 格式 | zip | ||
| 文件大小 | 59.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-25 00:00:00 | ||
图片预览





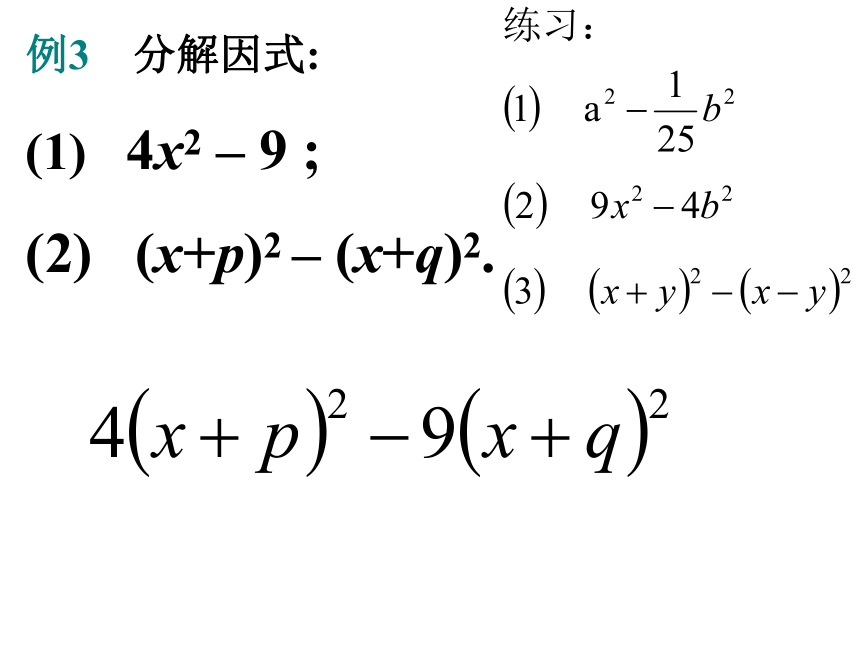
文档简介
课件12张PPT。(1)多项式6ab2+18a2b2-12a3b2c的公因式( )
(A)6ab2c (B)ab2 (C)6ab2 (D)6a3b2CC1.选择课后练习(2)分解因式6p(p+q)-4q(p+q)例3 把2a(b-c)-3(b-c)分解因式例4、把2a(b-c)+3(c-b)分解因式。(1) 2a(y-z)-3b(z-y)(2) 6(m-n)3-12(n-m)2练习:把下列各式分解因式:(3) 2(a-b)2 - a+b (4) 2(a-b)2 - (b-a)3 15.4.2 公式法导入新课(a+b)(a-b) = a2-b2a2-b2 =(a+b)(a-b) 两个数的平方差,等于这两个数的和与这两个数的差的积。整式乘法因式分解平方差公式进行因式分解: .下列多项式可以用平方差公式去分解因式吗? 为什么?(1) x2+y2 (2) x2-(-y)2
(3) -x2-y2 (4) -x2+y2
(5) a2-4 (6) a2+3小思考例3 分解因式:
4x2 – 9 ;
(2) (x+p)2 – (x+q)2.例4 分解因式:
(1)x4-y4;
(2) a3b – ab.2、分解因式:
xm+2-xm解:xm+2-xm
=xmx2-xm
=xm(x2-1)
=xm(x+1)(x-1)思维延伸
1. 观察下列各式:
32-12=8=8×1;
52-32=16=8×2;
72-52=24=8×3;
……
把你发现的规律用含n的等式表示出来.
2. 对于任意的自然数n,(n+7)2-(n-5)2能被24整除吗? 为什么?把下列各式分解因式
1、 x2-9y2
2、 4x2-9y2
3、-0.36x2+y2
4、x4-y2
5、 x2-(x-y)2
6、 9(x-y)2-y2
7、 16(a+b)2-9(a-b)2 小测验再见课件12张PPT。(1)多项式6ab2+18a2b2-12a3b2c的公因式( )
(A)6ab2c (B)ab2 (C)6ab2 (D)6a3b2CC1.选择课后练习(2)分解因式6p(p+q)-4q(p+q)例3 把2a(b-c)-3(b-c)分解因式例4、把2a(b-c)+3(c-b)分解因式。(1) 2a(y-z)-3b(z-y)(2) 6(m-n)3-12(n-m)2练习:把下列各式分解因式:(3) 2(a-b)2 - a+b (4) 2(a-b)2 - (b-a)3 15.4.2 公式法导入新课(a+b)(a-b) = a2-b2a2-b2 =(a+b)(a-b) 两个数的平方差,等于这两个数的和与这两个数的差的积。整式乘法因式分解平方差公式进行因式分解: .下列多项式可以用平方差公式去分解因式吗? 为什么?(1) x2+y2 (2) x2-(-y)2
(3) -x2-y2 (4) -x2+y2
(5) a2-4 (6) a2+3小思考例3 分解因式:
4x2 – 9 ;
(2) (x+p)2 – (x+q)2.例4 分解因式:
(1)x4-y4;
(2) a3b – ab.2、分解因式:
xm+2-xm解:xm+2-xm
=xmx2-xm
=xm(x2-1)
=xm(x+1)(x-1)思维延伸
1. 观察下列各式:
32-12=8=8×1;
52-32=16=8×2;
72-52=24=8×3;
……
把你发现的规律用含n的等式表示出来.
2. 对于任意的自然数n,(n+7)2-(n-5)2能被24整除吗? 为什么?把下列各式分解因式
1、 x2-9y2
2、 4x2-9y2
3、-0.36x2+y2
4、x4-y2
5、 x2-(x-y)2
6、 9(x-y)2-y2
7、 16(a+b)2-9(a-b)2 小测验再见
(A)6ab2c (B)ab2 (C)6ab2 (D)6a3b2CC1.选择课后练习(2)分解因式6p(p+q)-4q(p+q)例3 把2a(b-c)-3(b-c)分解因式例4、把2a(b-c)+3(c-b)分解因式。(1) 2a(y-z)-3b(z-y)(2) 6(m-n)3-12(n-m)2练习:把下列各式分解因式:(3) 2(a-b)2 - a+b (4) 2(a-b)2 - (b-a)3 15.4.2 公式法导入新课(a+b)(a-b) = a2-b2a2-b2 =(a+b)(a-b) 两个数的平方差,等于这两个数的和与这两个数的差的积。整式乘法因式分解平方差公式进行因式分解: .下列多项式可以用平方差公式去分解因式吗? 为什么?(1) x2+y2 (2) x2-(-y)2
(3) -x2-y2 (4) -x2+y2
(5) a2-4 (6) a2+3小思考例3 分解因式:
4x2 – 9 ;
(2) (x+p)2 – (x+q)2.例4 分解因式:
(1)x4-y4;
(2) a3b – ab.2、分解因式:
xm+2-xm解:xm+2-xm
=xmx2-xm
=xm(x2-1)
=xm(x+1)(x-1)思维延伸
1. 观察下列各式:
32-12=8=8×1;
52-32=16=8×2;
72-52=24=8×3;
……
把你发现的规律用含n的等式表示出来.
2. 对于任意的自然数n,(n+7)2-(n-5)2能被24整除吗? 为什么?把下列各式分解因式
1、 x2-9y2
2、 4x2-9y2
3、-0.36x2+y2
4、x4-y2
5、 x2-(x-y)2
6、 9(x-y)2-y2
7、 16(a+b)2-9(a-b)2 小测验再见课件12张PPT。(1)多项式6ab2+18a2b2-12a3b2c的公因式( )
(A)6ab2c (B)ab2 (C)6ab2 (D)6a3b2CC1.选择课后练习(2)分解因式6p(p+q)-4q(p+q)例3 把2a(b-c)-3(b-c)分解因式例4、把2a(b-c)+3(c-b)分解因式。(1) 2a(y-z)-3b(z-y)(2) 6(m-n)3-12(n-m)2练习:把下列各式分解因式:(3) 2(a-b)2 - a+b (4) 2(a-b)2 - (b-a)3 15.4.2 公式法导入新课(a+b)(a-b) = a2-b2a2-b2 =(a+b)(a-b) 两个数的平方差,等于这两个数的和与这两个数的差的积。整式乘法因式分解平方差公式进行因式分解: .下列多项式可以用平方差公式去分解因式吗? 为什么?(1) x2+y2 (2) x2-(-y)2
(3) -x2-y2 (4) -x2+y2
(5) a2-4 (6) a2+3小思考例3 分解因式:
4x2 – 9 ;
(2) (x+p)2 – (x+q)2.例4 分解因式:
(1)x4-y4;
(2) a3b – ab.2、分解因式:
xm+2-xm解:xm+2-xm
=xmx2-xm
=xm(x2-1)
=xm(x+1)(x-1)思维延伸
1. 观察下列各式:
32-12=8=8×1;
52-32=16=8×2;
72-52=24=8×3;
……
把你发现的规律用含n的等式表示出来.
2. 对于任意的自然数n,(n+7)2-(n-5)2能被24整除吗? 为什么?把下列各式分解因式
1、 x2-9y2
2、 4x2-9y2
3、-0.36x2+y2
4、x4-y2
5、 x2-(x-y)2
6、 9(x-y)2-y2
7、 16(a+b)2-9(a-b)2 小测验再见
