青岛版九年级数学下册 5.1.2函数与它的表示法 课件(共12张PPT)
文档属性
| 名称 | 青岛版九年级数学下册 5.1.2函数与它的表示法 课件(共12张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-17 11:07:18 | ||
图片预览




文档简介
(共15张PPT)
5.1 函数与它的表示法(2)
------函数概念及确定自变量的取值范围
回忆上一节课的三个例子,思考下列问题:
(1)在这些问题中,自变量可以取值的范围
分别是什么?
(2)对于自变量在它可以取值的范围内每取
一个值,另一个变量是否都有惟一确定的
值与它对应?
(3)由此你对函数有了哪些进一步的认识?
与同学交流.
新课导入
学习目标
1.进一步了解函数的概念;
2.能根据简单的函数表达式和问题情境,确定自变量可以取值的范围。
知识讲解
函数定义
在同一个变化过程中,有两个变量x,y. 如果对于变量x在可以取值的范围内每取 一个确定得值,变量y都有一个唯一确定的值与它对应,那么就说y是x的函数.
注意:(1)自变量“可以取值的范围”;
(2)对应关系:自变量每一个确定的
值,对应一个唯一确定的函数值。
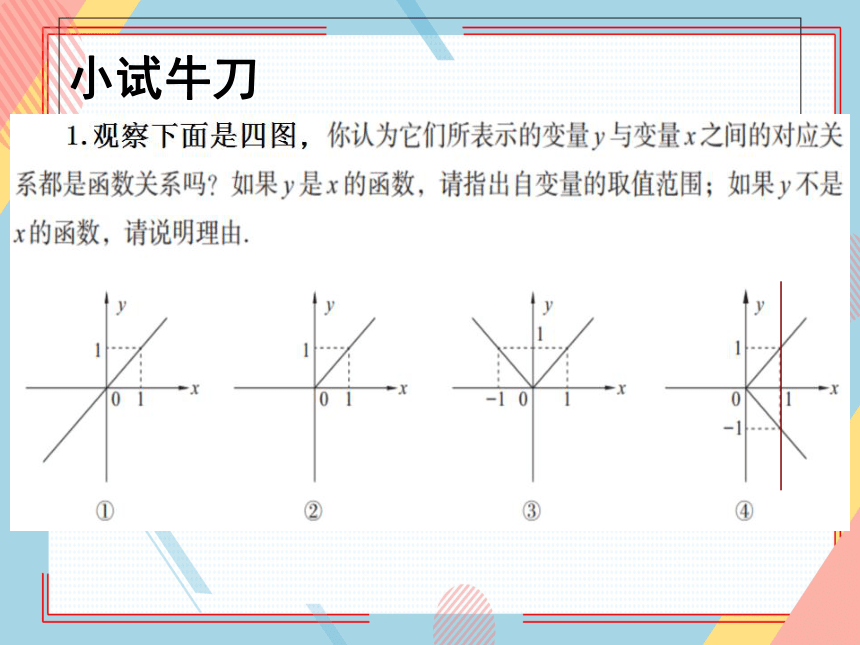
小试牛刀
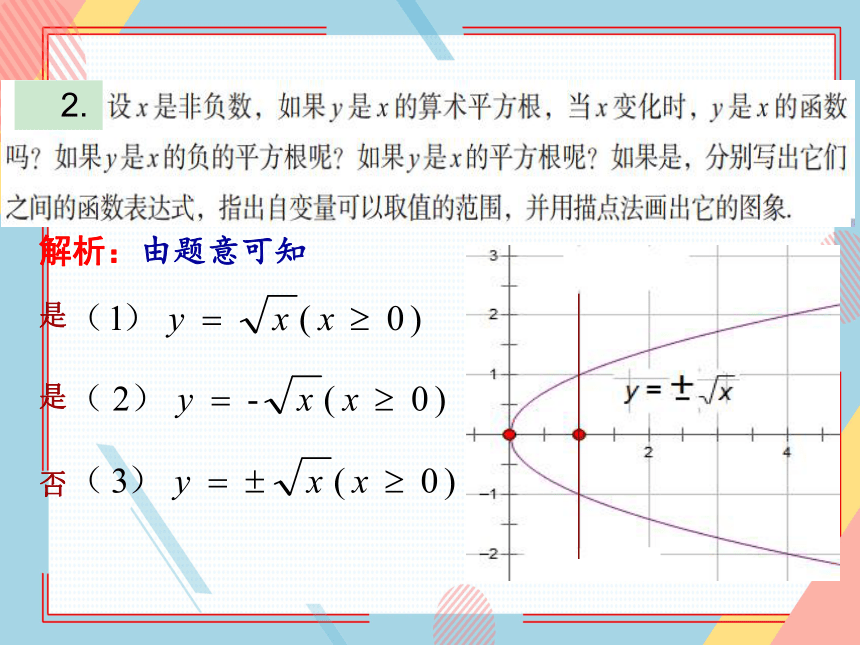
解析:由题意可知
是
是
否
2.
知识讲解
例1:求下列函数中自变量x可以取值的范围:
(1) y=3x-2
(2) y=
(3)y=
(4) y=
x取任意实数
x≥1
x<
小试牛刀
3:求下列函数中自变量x可以取值的范围:
(1) y=3x2+1
(2) y=
(3)y=
(4) y=
x取任意实数
x≥-2
挑战自我
解析:由题意可知当x为任意实数时, ;
则有一元二次方程 无解,故
,解得
变式训练
解析:由题意可知当x为任意实数时, ;
变形 ,因
故
随堂练习
教材第8页课后练习1、2、3题
本课小结
一、函数定义
在同一个变化过程中,有两个变量x,y. 如果对于变量x在可以取值的范围内每取 一个确定得值,变量y都有一个唯一确定的值与它对应,那么就说y是x的函数.
注意(1)自变量“可以取值的范围”;
(2)对应关系:自变量每一个确定的值,对应一个唯一
确定的函数值。
二、函数自变量取值范围的确定
(1)表达式为整式,自变量取全体实数;
(2)表达式为分式,要考虑分母不为零;
(3)表达式为二次根式,要考虑被开方数应为非负数;
(4)表达式为以上综合式子时,要充分考虑以上三种情况。
5.1 函数与它的表示法(2)
------函数概念及确定自变量的取值范围
回忆上一节课的三个例子,思考下列问题:
(1)在这些问题中,自变量可以取值的范围
分别是什么?
(2)对于自变量在它可以取值的范围内每取
一个值,另一个变量是否都有惟一确定的
值与它对应?
(3)由此你对函数有了哪些进一步的认识?
与同学交流.
新课导入
学习目标
1.进一步了解函数的概念;
2.能根据简单的函数表达式和问题情境,确定自变量可以取值的范围。
知识讲解
函数定义
在同一个变化过程中,有两个变量x,y. 如果对于变量x在可以取值的范围内每取 一个确定得值,变量y都有一个唯一确定的值与它对应,那么就说y是x的函数.
注意:(1)自变量“可以取值的范围”;
(2)对应关系:自变量每一个确定的
值,对应一个唯一确定的函数值。
小试牛刀
解析:由题意可知
是
是
否
2.
知识讲解
例1:求下列函数中自变量x可以取值的范围:
(1) y=3x-2
(2) y=
(3)y=
(4) y=
x取任意实数
x≥1
x<
小试牛刀
3:求下列函数中自变量x可以取值的范围:
(1) y=3x2+1
(2) y=
(3)y=
(4) y=
x取任意实数
x≥-2
挑战自我
解析:由题意可知当x为任意实数时, ;
则有一元二次方程 无解,故
,解得
变式训练
解析:由题意可知当x为任意实数时, ;
变形 ,因
故
随堂练习
教材第8页课后练习1、2、3题
本课小结
一、函数定义
在同一个变化过程中,有两个变量x,y. 如果对于变量x在可以取值的范围内每取 一个确定得值,变量y都有一个唯一确定的值与它对应,那么就说y是x的函数.
注意(1)自变量“可以取值的范围”;
(2)对应关系:自变量每一个确定的值,对应一个唯一
确定的函数值。
二、函数自变量取值范围的确定
(1)表达式为整式,自变量取全体实数;
(2)表达式为分式,要考虑分母不为零;
(3)表达式为二次根式,要考虑被开方数应为非负数;
(4)表达式为以上综合式子时,要充分考虑以上三种情况。
