青岛版八年级数学下册 11.3 图形的中心对称 课件(共13张PPT)
文档属性
| 名称 | 青岛版八年级数学下册 11.3 图形的中心对称 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 188.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-17 11:15:50 | ||
图片预览




文档简介
(共14张PPT)
第 11 章 图形的平移与旋转
11.3 图形的中心对称
1、在平面内,将一个图形绕一个定点按某一个方向(逆时针或顺时针方向)转动一定的角度,图形的这种变化叫做 ,这个定点叫做 ,这个角叫做 .
2、一个图形和它经过旋转所得到的图形中,对应点到旋转中心的距离 ;两组对应点分别与旋转中心的连线所成的角 .
回顾复习
旋转
旋转中心
旋转角
相等
相等
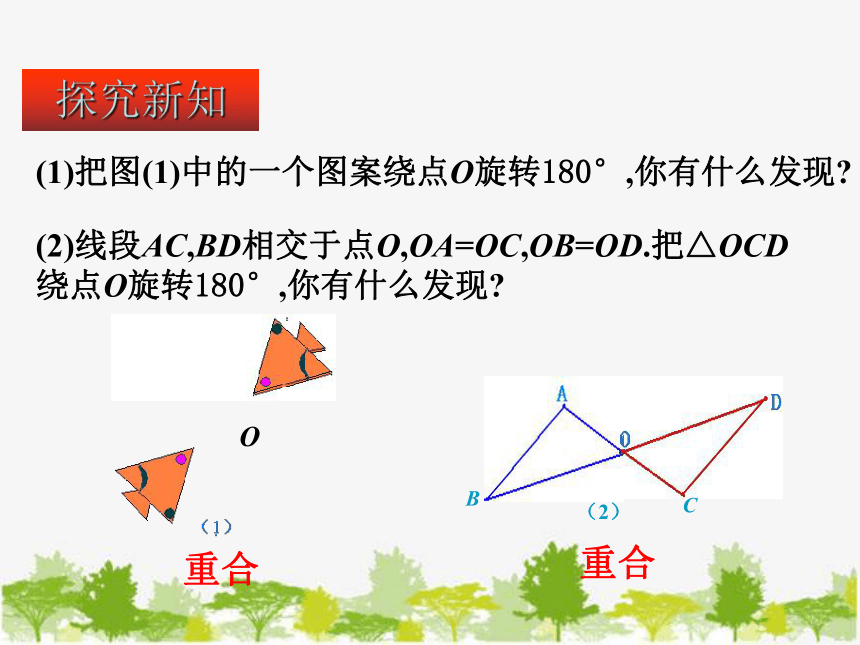
(1)把图(1)中的一个图案绕点O旋转180°,你有什么发现
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把△OCD绕点O旋转180°,你有什么发现
O
C
B
(2)
重合
重合
探究新知
在平面内将一个图形绕某一定点旋转180°,图形的这种变化叫做中心对称,这个定点叫做对称中心.一个图形经过中心对称能与另一个图形重合,就说这两个图形关于这个定点成中心对称.
中心对称是旋转变换的特殊情况,
成中心对称的两个图形是全等形.
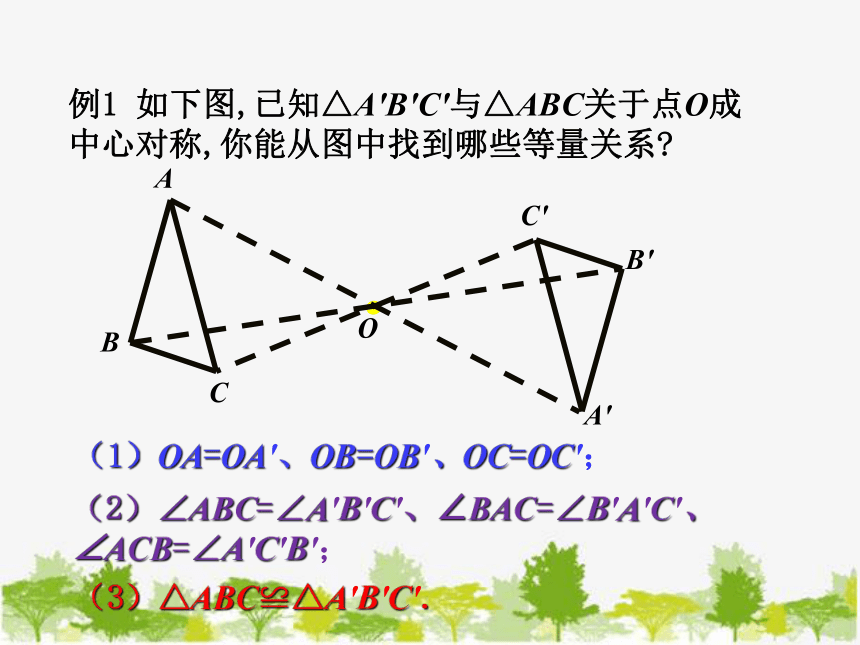
例1 如下图,已知△A'B'C'与△ABC关于点O成中心对称,你能从图中找到哪些等量关系
A'
B'
C'
A
B
C
O
(1)OA=OA'、OB=OB'、OC=OC';
(3)△ABC≌△A'B'C'.
(2)∠ABC=∠A'B'C'、∠BAC=∠B'A'C'、∠ACB=∠A'C'B';
(1)成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.
(2)成中心对称的两个图形是全等图形.
结论:
例2 如下图,△ABC和点O,画出与△ABC关于点O对称的△A′B′C′.
A′
C′
B′
△A′B′C′即为所求的三角形.
(1)连接AO并延长到A′,使OA ′=OA,
得到点A的对称点A′.
(2)同样画B、C的对称点 B′、C′.
(3)顺次连接各点.
画法:
分析:确定一个三角形需要几个点?画一个三角形关于某点成中心对称的三角形,需要画几个点的对称点呢?
你是如何理解“对称点所连线段都经过对称中心,而且被对称中心所平分”的?
例3(1)这些图形有什么共同的特征?
(2)将图上“风车”绕其上一点旋转180°,旋转前后的图形完全重合吗?
(1)在平面内,一个图形经过中心对称能与原来的图形重合,这个图形叫做中心对称图形.
O
B
A
C
D
(2)如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形.
课堂练习
1、下列图形中即是轴对称图形又是中心对称图形的是 ( )
A.角 B.等边三角形 C.线段 D.平行四边形
2、下列多边形中,是中心对称图形而不是轴对称图形的是 ( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
3、如下图,已知△ABC与△A′B′C′中心对称,求出它们的对称中心O.
A
B
C
A′
B′
C′
4、如右图,若矩形ABCD和矩形A'B'C'D'关于点A成中心对称,则四边形BDB'D'是菱形吗?为什么?
5、如下图,在矩形ABCD中,已知AB=2,AD=4,对角线AC,BD交于点O,EF经过点O交AD于点E,交BC于点F,求图中阴影部分的面积.
想一想,这节课你学到了什么?
课堂小结
第 11 章 图形的平移与旋转
11.3 图形的中心对称
1、在平面内,将一个图形绕一个定点按某一个方向(逆时针或顺时针方向)转动一定的角度,图形的这种变化叫做 ,这个定点叫做 ,这个角叫做 .
2、一个图形和它经过旋转所得到的图形中,对应点到旋转中心的距离 ;两组对应点分别与旋转中心的连线所成的角 .
回顾复习
旋转
旋转中心
旋转角
相等
相等
(1)把图(1)中的一个图案绕点O旋转180°,你有什么发现
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把△OCD绕点O旋转180°,你有什么发现
O
C
B
(2)
重合
重合
探究新知
在平面内将一个图形绕某一定点旋转180°,图形的这种变化叫做中心对称,这个定点叫做对称中心.一个图形经过中心对称能与另一个图形重合,就说这两个图形关于这个定点成中心对称.
中心对称是旋转变换的特殊情况,
成中心对称的两个图形是全等形.
例1 如下图,已知△A'B'C'与△ABC关于点O成中心对称,你能从图中找到哪些等量关系
A'
B'
C'
A
B
C
O
(1)OA=OA'、OB=OB'、OC=OC';
(3)△ABC≌△A'B'C'.
(2)∠ABC=∠A'B'C'、∠BAC=∠B'A'C'、∠ACB=∠A'C'B';
(1)成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.
(2)成中心对称的两个图形是全等图形.
结论:
例2 如下图,△ABC和点O,画出与△ABC关于点O对称的△A′B′C′.
A′
C′
B′
△A′B′C′即为所求的三角形.
(1)连接AO并延长到A′,使OA ′=OA,
得到点A的对称点A′.
(2)同样画B、C的对称点 B′、C′.
(3)顺次连接各点.
画法:
分析:确定一个三角形需要几个点?画一个三角形关于某点成中心对称的三角形,需要画几个点的对称点呢?
你是如何理解“对称点所连线段都经过对称中心,而且被对称中心所平分”的?
例3(1)这些图形有什么共同的特征?
(2)将图上“风车”绕其上一点旋转180°,旋转前后的图形完全重合吗?
(1)在平面内,一个图形经过中心对称能与原来的图形重合,这个图形叫做中心对称图形.
O
B
A
C
D
(2)如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形.
课堂练习
1、下列图形中即是轴对称图形又是中心对称图形的是 ( )
A.角 B.等边三角形 C.线段 D.平行四边形
2、下列多边形中,是中心对称图形而不是轴对称图形的是 ( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
3、如下图,已知△ABC与△A′B′C′中心对称,求出它们的对称中心O.
A
B
C
A′
B′
C′
4、如右图,若矩形ABCD和矩形A'B'C'D'关于点A成中心对称,则四边形BDB'D'是菱形吗?为什么?
5、如下图,在矩形ABCD中,已知AB=2,AD=4,对角线AC,BD交于点O,EF经过点O交AD于点E,交BC于点F,求图中阴影部分的面积.
想一想,这节课你学到了什么?
课堂小结
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
