4.2 二叉树的基本操作 课件-2021-2022学年浙教版(2019)高中信息技术选修1(24张PPT)
文档属性
| 名称 | 4.2 二叉树的基本操作 课件-2021-2022学年浙教版(2019)高中信息技术选修1(24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 131.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-04-16 18:57:11 | ||
图片预览







文档简介
(共24张PPT)
4.2 二叉树的基本操作
无论是线性结构还是非线性结构数据,都需要对数据元素逐个进行
组织存储和处理。
二叉树的基本操作,主要包括二叉树的建立和遍历等。
二叉树的建立
1.建立二叉树的操作,可以按照层的顺序进行,先由第1层开始,依次到
下一层,在每一层中按照从左到右的顺序创建节点。
二叉树的建立可以用数组或者链表数据结构来实现。
1.数组实现
用数组来表示二叉树时,分为以下两种情况。
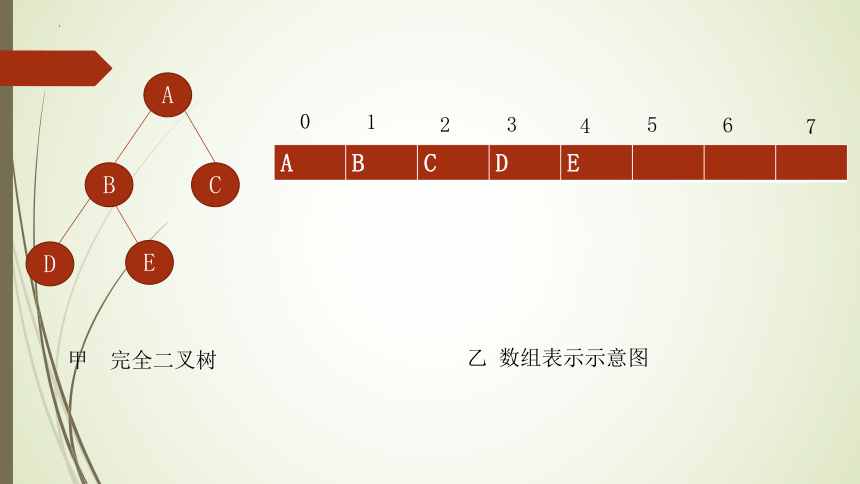
(1)完全二叉树
从二叉树的根节点开始,按从上而下、自左向右的顺序对n个节点进行编号,
根节点的编号为0,最后一个节点的编号为n-1。然后依次将二叉树的节点用
一组连续的数组元素来表示,节点编号与数组的下标一一对应。
如下图中图甲所示的完全二叉树所对应的一维数组表示如图乙所示。
A
B
C
D
E
甲 完全二叉树
A B C D E
0
1
2
3
4
5
6
7
乙 数组表示示意图
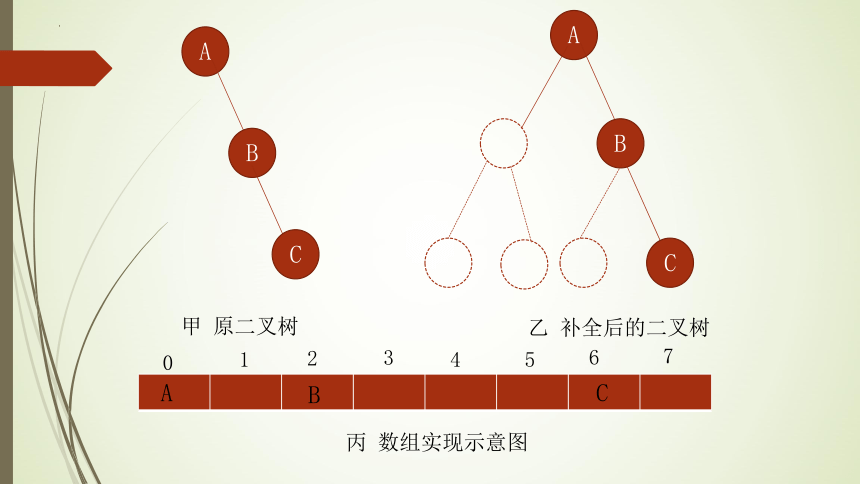
(2)非完全二叉树
对于非完全二叉树,先将它补充为一棵完全二叉树,补上的节点
及分支用虚线表示,如下图图甲所示的一棵非完全二叉树补全为
图乙所示的完全二叉树。然后将补全后的完全二叉树,从它的根
节点开始,按从上而下、自左往右的顺序对n个节点进行编号,
根节点的编号为0,最后一个节点的编号为n-1。如图丙所示,依
次把完全二叉树中原二叉树的节点用一维数组的各个元素来表示,
节点编号与数组的下标一一对应。
A
B
C
A
B
C
甲 原二叉树
乙 补全后的二叉树
0
1
2
3
4
5
6
7
丙 数组实现示意图
A
B
C
对于完全二叉树而言,一维数组的表示方式既简单又节省存储空间。
但对于一般的二叉树来说,采用一维数组表示时,结构虽然简单,
却容易造成存储空间的浪费。
如图甲所示,一个深度为k且只有k个节点的树需要如图乙所示2k-1个节点
的存储空间才能表示出来。
2.链表实现
二叉树也可以采用链表来实现,用任意一组存储单元来存储二叉树的节点,
用指向节点的指针来表示节点之间的关系。
由于二叉树的节点可能有两个孩子,即左孩子和右孩子,因此二叉树的节点
至少需要3个域:一个数据域和两个指针域。两个指针域分别指向节点的左
孩子和右孩子,这两个指针分别称为左指针和右指针,这样得到的链表也
称为二叉链表。
如下图所示的是二叉树及其对应的二叉链表实现示意图。
A
B
D
C
E
F
G
A
头指针
B
^
C
^
^
D
^
E
^
F
^
^
G
^
二叉树的list实现
二叉树节点可以看成是一个三元组,元素是左、右子树和本节点
数据。
Python的list可以用于组合这样的三个元素。
下面介绍用list构造二叉树的方法。
(1)空树用None表示。
(2)非空二叉树用包含三个元素的列表[d,l,r]表示,其中:d表示
根节点的元素,l和r是两棵子树,采用与整个二叉树同样结构的list
表示。
这样就可以把二叉树映射到一种分层的list结构,每棵二叉树都有与之对应的(递归结构的)list。
A
B
C
D
F
G
E
H
I
[‘A’,[‘B’,None,None],
[‘C’,[‘D’,[‘F’,None,None],
[‘G’,None,None]],
[‘E’,[‘H’,None,None],
[‘I’,None,None]]]]
二叉树的遍历
在完成二叉树的建立操作后,就可以对二叉树的各个节点进行访问,即遍历操作。
二叉树的遍历,是指按照一定的规则和次序访问二叉树中的所有节点,使得每个节点都被访问一次且仅被访问一次。按照不同的遍历方式对节点进行访问,其处理效率不完全相同。
二叉树的遍历方式有很多,主要有前序遍历、中序遍历和后序遍历等。
1.前序遍历
前序遍历的规则是:若二叉树为空,则空操作返回;否则,先访问
根节点,再访问左子树,最后访问右子树。
A
B
D
E
H
C
F
I
G
J
K
前序遍历顺序为:A-B-D-H-E-C-F-I-G-J-K
2.中序遍历
中序遍历的规则是:若二叉树为空,则空操作返回;否则,先访问
左子树,再访问根节点,最后访问右子树。
A
B
D
E
H
C
F
I
G
J
K
中序遍历顺序为:D-H-B-E-A-I-F-C-J-G-K
3. 后序遍历
后序遍历的规则是:若二叉树为空,则空操作返回;否则,先访问
左子树,再访问右子树,最后访问根节点。
A
B
D
E
H
C
F
I
G
J
K
后序遍历顺序为:H-D-E-B-I-F-J-K-G-C-A
如果选取其中一种遍历策略对二叉树进行遍历,对于二叉树的
左右子树,也需遵守该遍历原则,即二叉树的任意一个局部都
必须遵守该遍历原则。对一棵二叉树进行前序遍历时,根节点
总是处于遍历序列之首;中序遍历时根节点位置居中,左子树
的所有节点都在其左边,右子树的所有节点都在其右边;后序
遍历时根节点位置在最后,其所有节点都在其左边。
二叉树的应用
如果将数学表达式中的运算数和运算符视为二叉树的每个节点,
那么可以构造出各种表达式树。
+
-
8
4
/
5
+
3
*
2
6
中序遍历:8-(3+2*6)/5+4
中缀表达式
后序遍历:8 3 2 6 * + 5 / - 4 +
后缀表达式(逆波兰表达式)
计算机的处理规则简化为:从左到右依序完成计算,
并方便求得结果。
已知前序遍历序列和后序遍历序列,能否唯一确定一棵二叉树?
不能。假如将一棵二叉树看成由根节点与左、右子树(子节点)组成,
根据前序遍历和后序遍历序列都可找到根节点,但当左、右子树(子节
点)有一个为空时,则无法确定序列中的其他节点到底是位于左子树还
是右子树。
例如,某二叉树的根节点下仅有一个子节点,只知道前序遍历与后序遍
历,是无法确定该子节点到底是右子节点还是左子节点。
练一练
1.有如图所示的二叉树。用list表示该二叉树为:
A.[‘a’,’b’,’d’,’c’,’e’]
B.[‘a’,[‘b’,[‘c’,None,None],None],[‘d’,[‘e’]]]
C.[‘a’,[‘b’,[‘c’]],[‘d’,[‘e’,None,None]]]
D.[‘a’,[‘b’,[‘c’,None,None]],[‘d’,[‘e’,None,None]]]
a
b
c
d
e
D
2.表达式(3+5)*4-8/2的后缀表达式为:
A.3 5 + 4 * - 8 2 /
B.3 5 + 4 * 8 - 2 /
C.3 5 + 4 * 8 2 - /
D.3 5 + 4 * 8 2 / -
D
3.一棵二叉树的前序遍历序列是abdecfhg,后序遍历序列是debhfgca,
则根节点的右子树的节点个数可能是:
A.3
B.4
C.5
D.6
B
4.某棵二叉树用数组存储后如图所示:
数组下标 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
数组元素 F C A D E H G B
则节点D的左孩子节点为:
A.H
B.空
C.G
D.E
A
谢 谢
4.2 二叉树的基本操作
无论是线性结构还是非线性结构数据,都需要对数据元素逐个进行
组织存储和处理。
二叉树的基本操作,主要包括二叉树的建立和遍历等。
二叉树的建立
1.建立二叉树的操作,可以按照层的顺序进行,先由第1层开始,依次到
下一层,在每一层中按照从左到右的顺序创建节点。
二叉树的建立可以用数组或者链表数据结构来实现。
1.数组实现
用数组来表示二叉树时,分为以下两种情况。
(1)完全二叉树
从二叉树的根节点开始,按从上而下、自左向右的顺序对n个节点进行编号,
根节点的编号为0,最后一个节点的编号为n-1。然后依次将二叉树的节点用
一组连续的数组元素来表示,节点编号与数组的下标一一对应。
如下图中图甲所示的完全二叉树所对应的一维数组表示如图乙所示。
A
B
C
D
E
甲 完全二叉树
A B C D E
0
1
2
3
4
5
6
7
乙 数组表示示意图
(2)非完全二叉树
对于非完全二叉树,先将它补充为一棵完全二叉树,补上的节点
及分支用虚线表示,如下图图甲所示的一棵非完全二叉树补全为
图乙所示的完全二叉树。然后将补全后的完全二叉树,从它的根
节点开始,按从上而下、自左往右的顺序对n个节点进行编号,
根节点的编号为0,最后一个节点的编号为n-1。如图丙所示,依
次把完全二叉树中原二叉树的节点用一维数组的各个元素来表示,
节点编号与数组的下标一一对应。
A
B
C
A
B
C
甲 原二叉树
乙 补全后的二叉树
0
1
2
3
4
5
6
7
丙 数组实现示意图
A
B
C
对于完全二叉树而言,一维数组的表示方式既简单又节省存储空间。
但对于一般的二叉树来说,采用一维数组表示时,结构虽然简单,
却容易造成存储空间的浪费。
如图甲所示,一个深度为k且只有k个节点的树需要如图乙所示2k-1个节点
的存储空间才能表示出来。
2.链表实现
二叉树也可以采用链表来实现,用任意一组存储单元来存储二叉树的节点,
用指向节点的指针来表示节点之间的关系。
由于二叉树的节点可能有两个孩子,即左孩子和右孩子,因此二叉树的节点
至少需要3个域:一个数据域和两个指针域。两个指针域分别指向节点的左
孩子和右孩子,这两个指针分别称为左指针和右指针,这样得到的链表也
称为二叉链表。
如下图所示的是二叉树及其对应的二叉链表实现示意图。
A
B
D
C
E
F
G
A
头指针
B
^
C
^
^
D
^
E
^
F
^
^
G
^
二叉树的list实现
二叉树节点可以看成是一个三元组,元素是左、右子树和本节点
数据。
Python的list可以用于组合这样的三个元素。
下面介绍用list构造二叉树的方法。
(1)空树用None表示。
(2)非空二叉树用包含三个元素的列表[d,l,r]表示,其中:d表示
根节点的元素,l和r是两棵子树,采用与整个二叉树同样结构的list
表示。
这样就可以把二叉树映射到一种分层的list结构,每棵二叉树都有与之对应的(递归结构的)list。
A
B
C
D
F
G
E
H
I
[‘A’,[‘B’,None,None],
[‘C’,[‘D’,[‘F’,None,None],
[‘G’,None,None]],
[‘E’,[‘H’,None,None],
[‘I’,None,None]]]]
二叉树的遍历
在完成二叉树的建立操作后,就可以对二叉树的各个节点进行访问,即遍历操作。
二叉树的遍历,是指按照一定的规则和次序访问二叉树中的所有节点,使得每个节点都被访问一次且仅被访问一次。按照不同的遍历方式对节点进行访问,其处理效率不完全相同。
二叉树的遍历方式有很多,主要有前序遍历、中序遍历和后序遍历等。
1.前序遍历
前序遍历的规则是:若二叉树为空,则空操作返回;否则,先访问
根节点,再访问左子树,最后访问右子树。
A
B
D
E
H
C
F
I
G
J
K
前序遍历顺序为:A-B-D-H-E-C-F-I-G-J-K
2.中序遍历
中序遍历的规则是:若二叉树为空,则空操作返回;否则,先访问
左子树,再访问根节点,最后访问右子树。
A
B
D
E
H
C
F
I
G
J
K
中序遍历顺序为:D-H-B-E-A-I-F-C-J-G-K
3. 后序遍历
后序遍历的规则是:若二叉树为空,则空操作返回;否则,先访问
左子树,再访问右子树,最后访问根节点。
A
B
D
E
H
C
F
I
G
J
K
后序遍历顺序为:H-D-E-B-I-F-J-K-G-C-A
如果选取其中一种遍历策略对二叉树进行遍历,对于二叉树的
左右子树,也需遵守该遍历原则,即二叉树的任意一个局部都
必须遵守该遍历原则。对一棵二叉树进行前序遍历时,根节点
总是处于遍历序列之首;中序遍历时根节点位置居中,左子树
的所有节点都在其左边,右子树的所有节点都在其右边;后序
遍历时根节点位置在最后,其所有节点都在其左边。
二叉树的应用
如果将数学表达式中的运算数和运算符视为二叉树的每个节点,
那么可以构造出各种表达式树。
+
-
8
4
/
5
+
3
*
2
6
中序遍历:8-(3+2*6)/5+4
中缀表达式
后序遍历:8 3 2 6 * + 5 / - 4 +
后缀表达式(逆波兰表达式)
计算机的处理规则简化为:从左到右依序完成计算,
并方便求得结果。
已知前序遍历序列和后序遍历序列,能否唯一确定一棵二叉树?
不能。假如将一棵二叉树看成由根节点与左、右子树(子节点)组成,
根据前序遍历和后序遍历序列都可找到根节点,但当左、右子树(子节
点)有一个为空时,则无法确定序列中的其他节点到底是位于左子树还
是右子树。
例如,某二叉树的根节点下仅有一个子节点,只知道前序遍历与后序遍
历,是无法确定该子节点到底是右子节点还是左子节点。
练一练
1.有如图所示的二叉树。用list表示该二叉树为:
A.[‘a’,’b’,’d’,’c’,’e’]
B.[‘a’,[‘b’,[‘c’,None,None],None],[‘d’,[‘e’]]]
C.[‘a’,[‘b’,[‘c’]],[‘d’,[‘e’,None,None]]]
D.[‘a’,[‘b’,[‘c’,None,None]],[‘d’,[‘e’,None,None]]]
a
b
c
d
e
D
2.表达式(3+5)*4-8/2的后缀表达式为:
A.3 5 + 4 * - 8 2 /
B.3 5 + 4 * 8 - 2 /
C.3 5 + 4 * 8 2 - /
D.3 5 + 4 * 8 2 / -
D
3.一棵二叉树的前序遍历序列是abdecfhg,后序遍历序列是debhfgca,
则根节点的右子树的节点个数可能是:
A.3
B.4
C.5
D.6
B
4.某棵二叉树用数组存储后如图所示:
数组下标 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
数组元素 F C A D E H G B
则节点D的左孩子节点为:
A.H
B.空
C.G
D.E
A
谢 谢
