4.3 抽象数据类型 课件-2021-2022学年浙教版(2019)高中信息技术选修1(19张PPT)
文档属性
| 名称 | 4.3 抽象数据类型 课件-2021-2022学年浙教版(2019)高中信息技术选修1(19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 117.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-04-16 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
4.3 抽象数据类型
在程序开发实践中,仅有计算层面的抽象还不够,还需要考虑数据层面
的抽象。抽象数据类型能够将数据定义表示与数据操作实现分离,以更
好地支持程序的模块化组织,它也是分解和实现大型复杂系统的最重要
基础技术。
Sum( )
Average( )
Sin( )
tan( )
cos( )
数据类型与抽象数据类型
数据类型是程序设计领域最重要的基本概念之一,它是指一组性质
相同的值的集合及定义在此集合上的一些操作的总称。使用计算机
程序处理的数据,通常属于不同的类型,如整数型、浮点数型或逻
辑型等。
每种程序设计语言都提供了一些内置数据类型,并为每个内置类型
提供了一批操作。例如,有下列Python程序语句:
a=13 #语句1
b=10 #语句2
c=a+b #语句3
print(c)
整型变量
抽象是指抽取出事物具有的普遍性本质,是对具体事物的一个概括。
抽象是一种思考问题的方式,它隐藏了繁杂的细节,只保留实现目标
所必需的信息,实现抽象化后有利于对事物的抽象,便于实现功能、
提高模块独立性。
人们对已有数据类型进行抽象,就有了抽象数据类型。
抽象数据类型(Abstract Data Type,简称ADT)是指一个数学
模型及定义在该模型上的一组操作。ADT的基本思想是抽象,它的
定义仅取决于它的一组逻辑特性,把数据结构及其操作作为一个整体
来研究,而与其在计算机内部如何表示和实现无关。
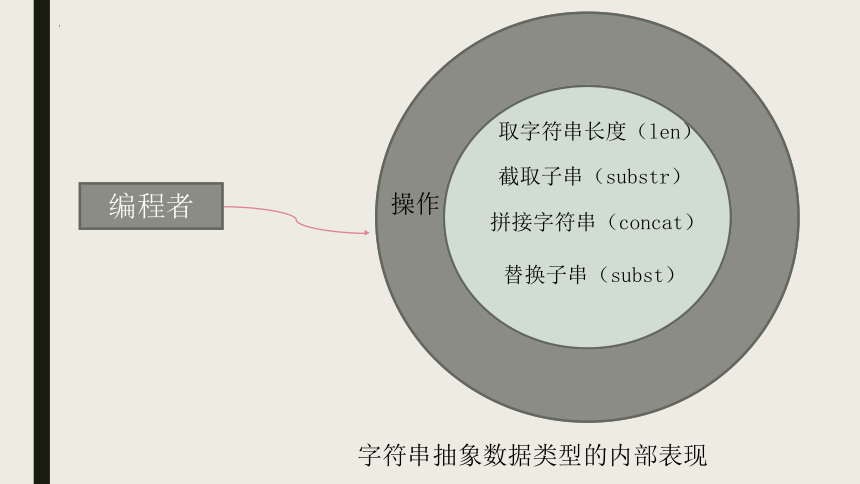
取字符串长度(len)
截取子串(substr)
拼接字符串(concat)
替换子串(subst)
操作
编程者
字符串抽象数据类型的内部表现
抽象数据类型除了那些已经定义并实现的数据类型,还可以是
编程者在程序设计时使用的函数或者单独定义的数据类型等。
如使用Python的内建函数时,编程者只需考虑函数的功能是否满
足实际需要,再确保函数调用时的表达式是否符合函数构造的要
求,就可以使用此函数,而不需要知道该函数内部实现的任何具
体细节。
max( )
insert( )
head( )
plot( )
根据抽象数据类型的定义,它还包括定义在该模型上的一组操作,
即一个数据对象、数据对象中各数据元素之间的关系及对数据元素
的操作。
唱歌
跳跃
吃饭
抽象数据类型的描述
定义一个抽象数据类型,需要清晰地表述出各方面的形式要求(如
操作的名字、参数的个数和类型等)和功能要求(希望这个操作完
成什么样的计算或产生什么效果等)。这类对象的功能体现为一组
可以对它们使用的操作。当然,还需要为这一抽象数据类型确定一
个类型名。
为了便于对抽象数据类型进行规范的描述,下面给出了描述抽象数
据类型的标准格式:
ADT 抽象数据类型名:
Data
数据元素之间逻辑关系的定义
Operation
操作1
初始条件
操作结果描述
操作2
……
操作n
……
endADT
在前三章有关线性表数据结构的学习中,已经知道了线性表数据结构会
涉及的一些操作。比如:
1.如何为创建操作提供初始元素序列;
2.检查线性表中是否存在某个特定数据对象;
3.改变线性表中的内容,包括加入新元素或删除已有元素等;
4.实现一个或两个表的操作,包括表的组合操作等;
5.实现对线性表中的每一个元素的操作,即对表元素的遍历。
下面呈现的是一个简单的线性表抽象数据类型,其中定义了一组
最基本的操作。
ADT List:
List(self) #创建一个新表
is_empty(self) #判断sellf是否为一个空表
len(self) #返回表的长度
prepend(self,elem) #在表头插入元素elem
append(self,elem) #在表尾插入元素elem
insert(self,elem,i) #在表的第i个位置插入元素elem
del_first(self) #删除第一个元素
del_last(self) #删除最后一个元素
del(self,i) #删除第i个元素
search(self,elem) #查找元素elem在表中第一次出现的位置
forall(self,op) #对表中的每个元素执行op操作
抽象数据类型的作用
抽象数据类型主要体现了程序设计中问题分解、抽象和信息隐藏
的特征。它把实际生活中的问题分解成多个规模较小且容易处理
的问题,然后建立一个计算机能处理的数据模型,把每个功能模
块作为一个独立单元,隐藏具体的实现过程,通过一次或多次的
模块调用来实现整个问题的解决。
抽象数据类型能给算法和程序设计带来很多好处,主要有:使用
抽象数据类型编写出来的程序结构清晰、层次分明,便于程序正
确性的证明和复杂性的分析;因为其模块化的特点,在程序设计
中容易纠正,具有很好的可维护性;由于抽象数据类型的表示和
实现都可以封装起来,便于移植和重用;因为算法设计与数据结
构设计的隔开,降低了算法和程序设计的复杂度,有助于在开发
过程中少出差错,保证编写的程序有较高的可靠性,同时,允许
数据结构的自由选择,给了算法的优化空间,提高了程序运行的
效率。
拓展链接
常见数据结构中的抽象数据类型定义
一个简单的字符串ADT,其中定义了一些字符串操作:
ADT String:
String(self,sseq) #基于字符序列sseq建立一个字符串
is_empty(self) #判断本字符串是否空串
len(self) #取得字符串的长度
char(self,index) #取得字符串中位置index的字符
substr(self,a,b) #取得字符串中[a:b]的子串,左闭右开区间
match(self,string) #查找串string在本字符串中第一次出现的
位置
concat(self,string) #获得本字符串与另一个字符串string的拼
接串
subst(self,str1,str2) #获得将本字符串里的子串str1替换为
str2的结果串
队列的操作通常采用另一套习惯的操作名(enqueue/dequeuer/peek)。
下面为一个简单的队列抽象数据类型:
ADT Queue:
Queue(self) #创建空队列
is_empty(self) #判断队列是否为空,空时返回True,
否则返回False
enqueue(self,elem) #将元素elem加入队列,即入队
dequeue(self) #删除队列里最早进的元素并将其 返回,即出队
peek(self) #查看队列里最早进入的元素,不删 除
定义二叉树抽象数据类型时,主要考虑如下几个方面:
节点是二叉树的基础,通常主要用节点保存与应用有关的信息;
作为二叉树的表示,还需要记录二叉树的结构信息,至少需要
保证能够检查节点的父子关系,例如,能从一个节点找到其左/右子节点。下面是一个基本的二叉树抽象数据类型的定义:
ADT BinTree: #一个二叉树抽象数据类型
BinTree(self,data,left,right) #构造操作,创建一个新二叉树
is_empty(self) #判断self是否为一个空二叉树
num_nodes(self) #求二叉树的节点个数
data(self) #获取二叉树根节点存储的数据
left(self) #获得二叉树的左子树
right(self) #获得二叉树的右子树
self_left(self,btree) #用btree取代原来的左子树
self_right(self,btree) #用btree取代原来的右子树
traversal(self) #遍历二叉树中各节点数据的迭代器
forall(self,op) #对二叉树中的每个节点的数据执行op操作
练一练
1.下列关于抽象数据类型的说法,不正确的是( )
A.程序设计语言的一个内置类型可以看作是一个抽象数据类型
B.抽象数据类型的定义仅取决于它的一组逻辑特性,与其在计算机
内部的表示与实现无关
C.定义一个抽象数据类型,只需要清晰地表达出各方面的形式要求
即可
D.使用抽象数据类型编写的程序结构清晰、层次分明,也便于程序
的移植和重用
C
2.创建一个简单的ADT,如下所示:
classNd( ):
def _init_(self,data):
self.data=data
def judge(self):
if self.data%5==0:
print(self.data,“是5的倍数”)
else:
print(self.data,“不是5的倍数”)
#创建实例
my_data=Nd(10)
my_data.judgeodd( )
下列有关该抽象数据类型(ADT)实例的说法中,不正确的是( )
A.创建的类名称为Nd B.def judge(self)的功能是定义judge函数
C.程序代码执行后的结果为“10是5的倍数”
D.my_data为Nd类的一个对象
B
谢 谢
4.3 抽象数据类型
在程序开发实践中,仅有计算层面的抽象还不够,还需要考虑数据层面
的抽象。抽象数据类型能够将数据定义表示与数据操作实现分离,以更
好地支持程序的模块化组织,它也是分解和实现大型复杂系统的最重要
基础技术。
Sum( )
Average( )
Sin( )
tan( )
cos( )
数据类型与抽象数据类型
数据类型是程序设计领域最重要的基本概念之一,它是指一组性质
相同的值的集合及定义在此集合上的一些操作的总称。使用计算机
程序处理的数据,通常属于不同的类型,如整数型、浮点数型或逻
辑型等。
每种程序设计语言都提供了一些内置数据类型,并为每个内置类型
提供了一批操作。例如,有下列Python程序语句:
a=13 #语句1
b=10 #语句2
c=a+b #语句3
print(c)
整型变量
抽象是指抽取出事物具有的普遍性本质,是对具体事物的一个概括。
抽象是一种思考问题的方式,它隐藏了繁杂的细节,只保留实现目标
所必需的信息,实现抽象化后有利于对事物的抽象,便于实现功能、
提高模块独立性。
人们对已有数据类型进行抽象,就有了抽象数据类型。
抽象数据类型(Abstract Data Type,简称ADT)是指一个数学
模型及定义在该模型上的一组操作。ADT的基本思想是抽象,它的
定义仅取决于它的一组逻辑特性,把数据结构及其操作作为一个整体
来研究,而与其在计算机内部如何表示和实现无关。
取字符串长度(len)
截取子串(substr)
拼接字符串(concat)
替换子串(subst)
操作
编程者
字符串抽象数据类型的内部表现
抽象数据类型除了那些已经定义并实现的数据类型,还可以是
编程者在程序设计时使用的函数或者单独定义的数据类型等。
如使用Python的内建函数时,编程者只需考虑函数的功能是否满
足实际需要,再确保函数调用时的表达式是否符合函数构造的要
求,就可以使用此函数,而不需要知道该函数内部实现的任何具
体细节。
max( )
insert( )
head( )
plot( )
根据抽象数据类型的定义,它还包括定义在该模型上的一组操作,
即一个数据对象、数据对象中各数据元素之间的关系及对数据元素
的操作。
唱歌
跳跃
吃饭
抽象数据类型的描述
定义一个抽象数据类型,需要清晰地表述出各方面的形式要求(如
操作的名字、参数的个数和类型等)和功能要求(希望这个操作完
成什么样的计算或产生什么效果等)。这类对象的功能体现为一组
可以对它们使用的操作。当然,还需要为这一抽象数据类型确定一
个类型名。
为了便于对抽象数据类型进行规范的描述,下面给出了描述抽象数
据类型的标准格式:
ADT 抽象数据类型名:
Data
数据元素之间逻辑关系的定义
Operation
操作1
初始条件
操作结果描述
操作2
……
操作n
……
endADT
在前三章有关线性表数据结构的学习中,已经知道了线性表数据结构会
涉及的一些操作。比如:
1.如何为创建操作提供初始元素序列;
2.检查线性表中是否存在某个特定数据对象;
3.改变线性表中的内容,包括加入新元素或删除已有元素等;
4.实现一个或两个表的操作,包括表的组合操作等;
5.实现对线性表中的每一个元素的操作,即对表元素的遍历。
下面呈现的是一个简单的线性表抽象数据类型,其中定义了一组
最基本的操作。
ADT List:
List(self) #创建一个新表
is_empty(self) #判断sellf是否为一个空表
len(self) #返回表的长度
prepend(self,elem) #在表头插入元素elem
append(self,elem) #在表尾插入元素elem
insert(self,elem,i) #在表的第i个位置插入元素elem
del_first(self) #删除第一个元素
del_last(self) #删除最后一个元素
del(self,i) #删除第i个元素
search(self,elem) #查找元素elem在表中第一次出现的位置
forall(self,op) #对表中的每个元素执行op操作
抽象数据类型的作用
抽象数据类型主要体现了程序设计中问题分解、抽象和信息隐藏
的特征。它把实际生活中的问题分解成多个规模较小且容易处理
的问题,然后建立一个计算机能处理的数据模型,把每个功能模
块作为一个独立单元,隐藏具体的实现过程,通过一次或多次的
模块调用来实现整个问题的解决。
抽象数据类型能给算法和程序设计带来很多好处,主要有:使用
抽象数据类型编写出来的程序结构清晰、层次分明,便于程序正
确性的证明和复杂性的分析;因为其模块化的特点,在程序设计
中容易纠正,具有很好的可维护性;由于抽象数据类型的表示和
实现都可以封装起来,便于移植和重用;因为算法设计与数据结
构设计的隔开,降低了算法和程序设计的复杂度,有助于在开发
过程中少出差错,保证编写的程序有较高的可靠性,同时,允许
数据结构的自由选择,给了算法的优化空间,提高了程序运行的
效率。
拓展链接
常见数据结构中的抽象数据类型定义
一个简单的字符串ADT,其中定义了一些字符串操作:
ADT String:
String(self,sseq) #基于字符序列sseq建立一个字符串
is_empty(self) #判断本字符串是否空串
len(self) #取得字符串的长度
char(self,index) #取得字符串中位置index的字符
substr(self,a,b) #取得字符串中[a:b]的子串,左闭右开区间
match(self,string) #查找串string在本字符串中第一次出现的
位置
concat(self,string) #获得本字符串与另一个字符串string的拼
接串
subst(self,str1,str2) #获得将本字符串里的子串str1替换为
str2的结果串
队列的操作通常采用另一套习惯的操作名(enqueue/dequeuer/peek)。
下面为一个简单的队列抽象数据类型:
ADT Queue:
Queue(self) #创建空队列
is_empty(self) #判断队列是否为空,空时返回True,
否则返回False
enqueue(self,elem) #将元素elem加入队列,即入队
dequeue(self) #删除队列里最早进的元素并将其 返回,即出队
peek(self) #查看队列里最早进入的元素,不删 除
定义二叉树抽象数据类型时,主要考虑如下几个方面:
节点是二叉树的基础,通常主要用节点保存与应用有关的信息;
作为二叉树的表示,还需要记录二叉树的结构信息,至少需要
保证能够检查节点的父子关系,例如,能从一个节点找到其左/右子节点。下面是一个基本的二叉树抽象数据类型的定义:
ADT BinTree: #一个二叉树抽象数据类型
BinTree(self,data,left,right) #构造操作,创建一个新二叉树
is_empty(self) #判断self是否为一个空二叉树
num_nodes(self) #求二叉树的节点个数
data(self) #获取二叉树根节点存储的数据
left(self) #获得二叉树的左子树
right(self) #获得二叉树的右子树
self_left(self,btree) #用btree取代原来的左子树
self_right(self,btree) #用btree取代原来的右子树
traversal(self) #遍历二叉树中各节点数据的迭代器
forall(self,op) #对二叉树中的每个节点的数据执行op操作
练一练
1.下列关于抽象数据类型的说法,不正确的是( )
A.程序设计语言的一个内置类型可以看作是一个抽象数据类型
B.抽象数据类型的定义仅取决于它的一组逻辑特性,与其在计算机
内部的表示与实现无关
C.定义一个抽象数据类型,只需要清晰地表达出各方面的形式要求
即可
D.使用抽象数据类型编写的程序结构清晰、层次分明,也便于程序
的移植和重用
C
2.创建一个简单的ADT,如下所示:
classNd( ):
def _init_(self,data):
self.data=data
def judge(self):
if self.data%5==0:
print(self.data,“是5的倍数”)
else:
print(self.data,“不是5的倍数”)
#创建实例
my_data=Nd(10)
my_data.judgeodd( )
下列有关该抽象数据类型(ADT)实例的说法中,不正确的是( )
A.创建的类名称为Nd B.def judge(self)的功能是定义judge函数
C.程序代码执行后的结果为“10是5的倍数”
D.my_data为Nd类的一个对象
B
谢 谢
