北师大版数学七年级下册第1-5单元测试卷(含答案)
文档属性
| 名称 | 北师大版数学七年级下册第1-5单元测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-16 21:43:06 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
北师大七年级下学期阶段诊断卷(五)
考试范围:第1—5单元;考试时间:100分钟
一.选择题(每题3分,共30分)
1.下列图形中不是轴对称图形的是( )
A B C D
2.下列四句话的文字有三句具有对称规律,其中没有这种规律的一句是( )
A.有志者事竟成 B.上海自来水来自海上
C.清水池里池水清 D.蜜蜂酿蜂蜜
3.若m、n均为正整数且,,则的值为( )
A.10 B.11 C.12 D.13
4.已知△ABC的三边长分别为4、4、6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )条.
A.3 B.4 C.5 D.6
5.如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA、BC于点G、H;再分别以点G、H为圆心,大于GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.若∠A=100°,则∠EBC度数为( )
A.50° B.40° C.30° D.80°
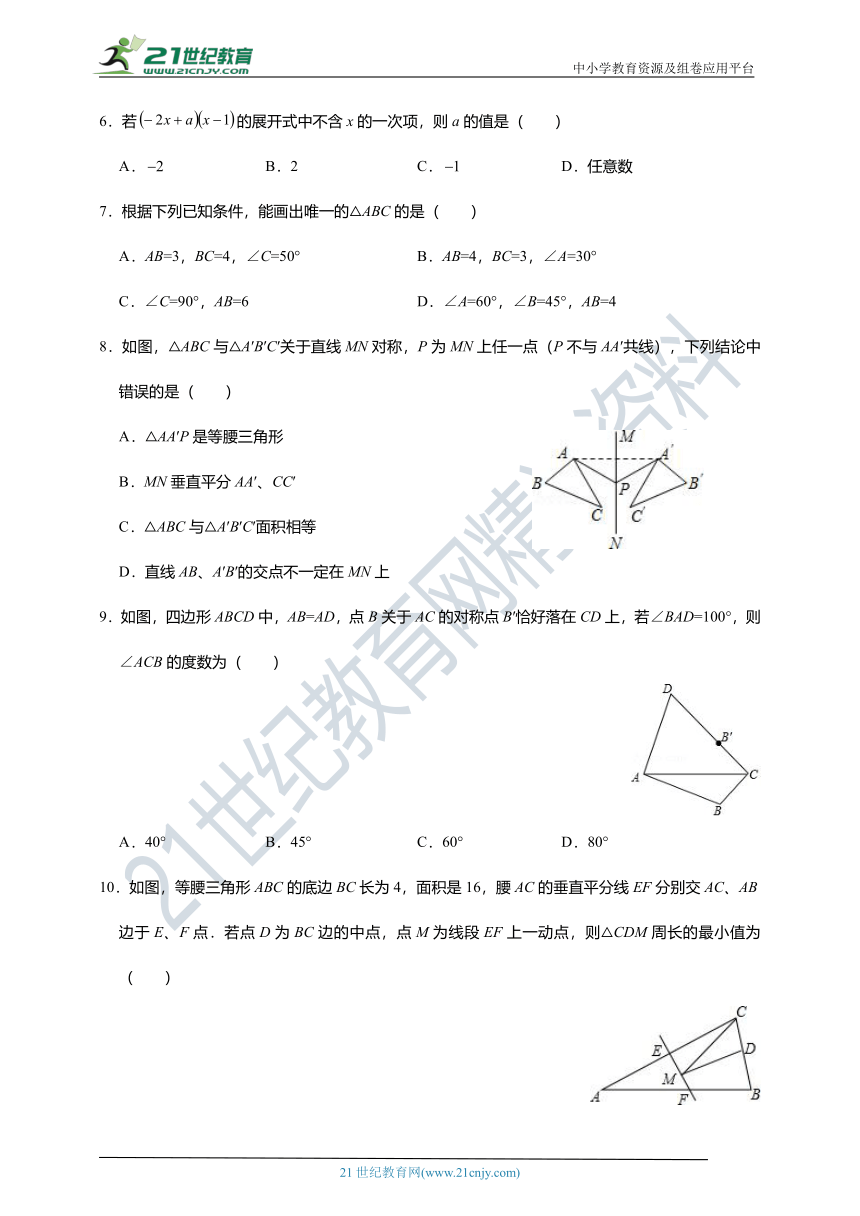
6.若的展开式中不含x的一次项,则a的值是( )
A. B.2 C. D.任意数
7.根据下列已知条件,能画出唯一的△ABC的是( )
A.AB=3,BC=4,∠C=50° B.AB=4,BC=3,∠A=30°
C.∠C=90°,AB=6 D.∠A=60°,∠B=45°,AB=4
8.如图,△ABC与△A′B′C′关于直线MN对称,P为MN上任一点(P不与AA′共线),下列结论中错误的是( )
A.△AA′P是等腰三角形
B.MN垂直平分AA′、CC′
C.△ABC与△A′B′C′面积相等
D.直线AB、A′B′的交点不一定在MN上
9.如图,四边形ABCD中,AB=AD,点B关于AC的对称点B′恰好落在CD上,若∠BAD=100°,则∠ACB的度数为( )
A.40° B.45° C.60° D.80°
10.如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC、AB边于E、F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
A.6 B.8 C.10 D.12
二.填空题(每题3分,共15分)
11.小明在平面镜里看到背后墙上电子钟显示的时间如图所示,此刻的实际时间应该是_____________.
12.如图所示,AB∥CE,∠C=35°,∠A=115°,那么∠F=_________°.
13.如图,在5×2方格纸中,有一个以格点为顶点的△ABC,请你找出方格纸中所有与△ABC成轴对称且以格点为顶点的三角形,这样的三角形共有____________个.
14.若,,则M与N的大小关系为_______________.
15.如图,是小明从学校到家里行进的路程s(米)与时间t(分)的图象.观察图象,从中得到如下信息:
①学校离小明家1000米;
②小明用了20分钟到家;
③小明前10分钟走了路程的一半;
④小明后10分钟比前10分钟走得快,
其中正确的有___________________(填序号).
三.解答题(共55分)
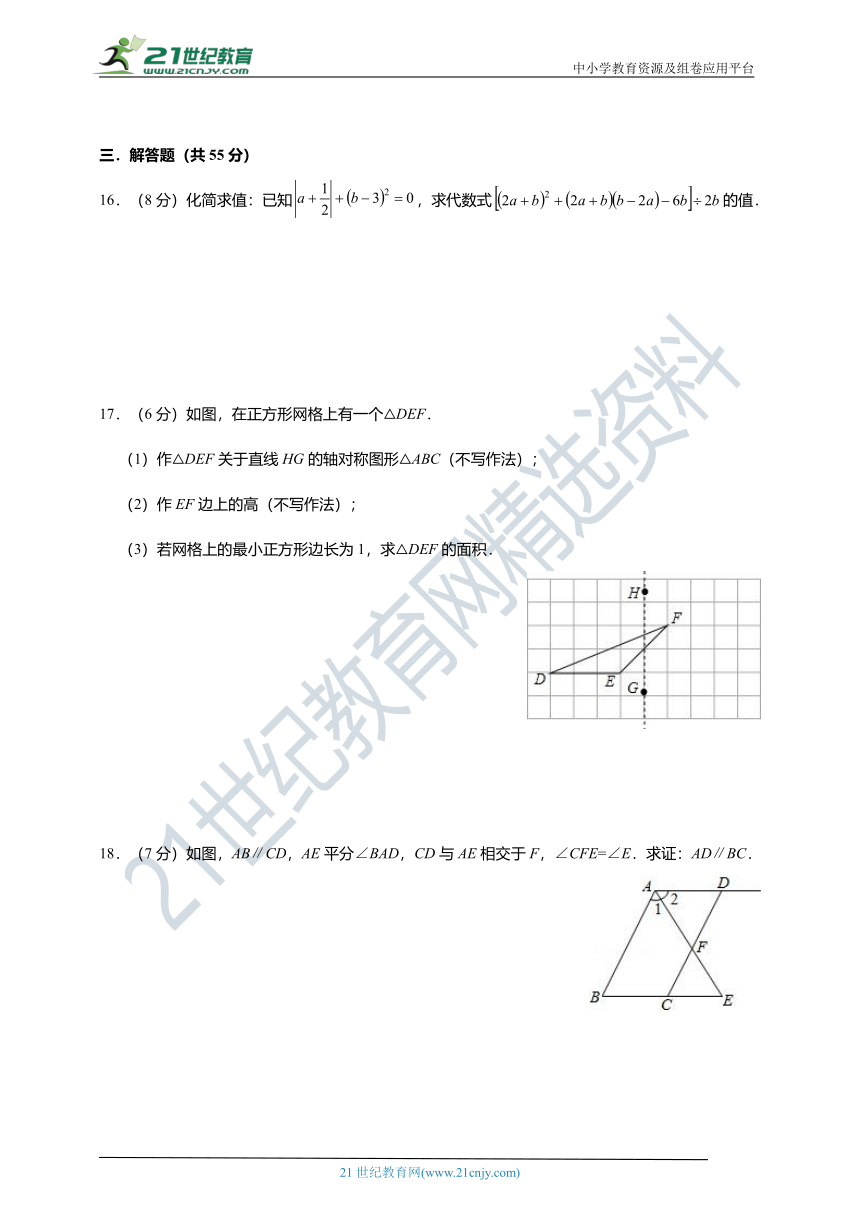
16.(8分)化简求值:已知,求代数式的值.
17.(6分)如图,在正方形网格上有一个△DEF.
(1)作△DEF关于直线HG的轴对称图形△ABC(不写作法);
(2)作EF边上的高(不写作法);
(3)若网格上的最小正方形边长为1,求△DEF的面积.
18.(7分)如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD∥BC.
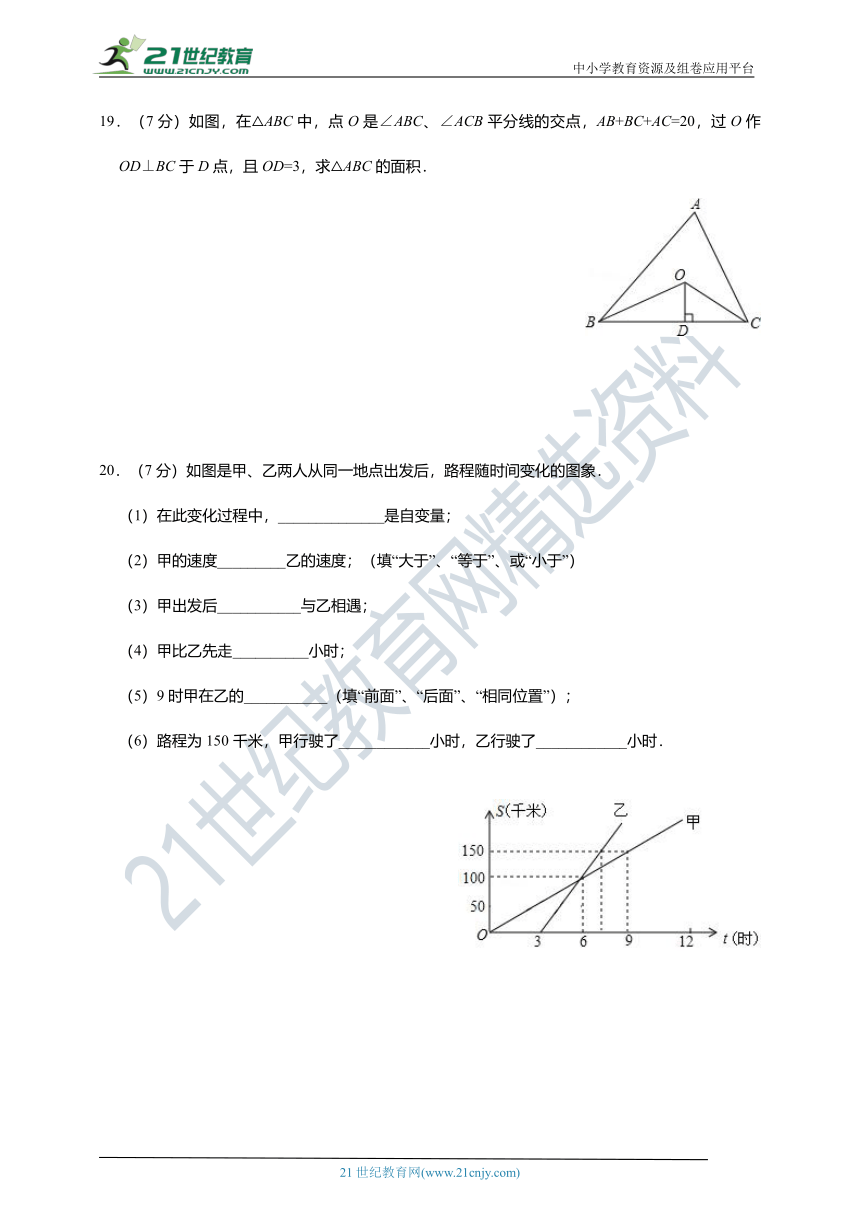
19.(7分)如图,在△ABC中,点O是∠ABC、∠ACB平分线的交点,AB+BC+AC=20,过O作OD⊥BC于D点,且OD=3,求△ABC的面积.
20.(7分)如图是甲、乙两人从同一地点出发后,路程随时间变化的图象.
(1)在此变化过程中,______________是自变量;
(2)甲的速度_________乙的速度;(填“大于”、“等于”、或“小于”)
(3)甲出发后___________与乙相遇;
(4)甲比乙先走__________小时;
(5)9时甲在乙的___________(填“前面”、“后面”、“相同位置”);
(6)路程为150千米,甲行驶了____________小时,乙行驶了____________小时.
21.(10分)已知,如图,△ABC是等边三角形,点D是AC的中点,延长BC到E,使CE=CD,连接DE,过点D作DM⊥BE于M.
(1)求∠E的度数.
(2)求证:BM=EM.
22.(10分)如图,在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA.
(1)求证:∠BAD=∠EDC;
(2)作出点E关于直线BC的对称点M,连接DM、AM,猜想DM与AM的数量关系,并说明理由.
参考答案
一.选择题(共10小题,每题3分,共30分)
A.A.B.B.B. A.D.D.A.C.
二.填空题(共5小题)
11.21:05.
12.80.
13.4.
14.M>N.
15.①,②,④.
三.解答题(共7小题,共55分)
16.解:∵|a|+(b+3)2=0,
∴a0,b﹣3=0, ∴a,b=3,
[(2a+b)2+(2a+b)(b﹣2a)﹣6b]÷2b,
=(4a2+b2+4ab+b2﹣4a2﹣6b)÷2b,=b+2a﹣3,
把a,b=3代入得:原式=b+2a﹣3=3+2×()﹣3=﹣1;
17.解:(1)所作图形如图所示:
△ABC即为所作图形;
(2)所作图形如图所示:
DM即为EF边上的高;
(3)S△DEF3×2=3.
18.证明:∵AE平分∠BAD, ∴∠1=∠2,
∵AB∥CD,∠CFE=∠E, ∴∠1=∠CFE=∠E,
∴∠2=∠E, ∴AD∥BC.
19.解:如图,过点O作OE⊥AB于E,OF⊥AC于F,连接OA.
∵点O是∠ABC,∠ACB平分线的交点,∴OE=OD,OF=OD,即OE=OF=OD=3,
∴S△ABC=S△ABO+S△BCO+S△ACOAB OEBC ODAC OF
2×(AB+BC+AC)3×20=30.
20.解:(1)函数图象反映路程随时间变化的图象,则t是自变量,s为因变量;
(2)甲的速度千米/小时,所以甲的速度小于乙的速度;
(3)6时表示他们相遇,即乙追赶上了甲;
(4)甲比乙先走3小时;
(5)t=9时,乙的图象在甲的上方,即乙行驶的路程远些,所以9时甲在乙的后面;
(6)路程为150千米,甲行驶了9时,乙行驶的时间为:150÷(100÷3)=4.5(小时).
故答案为:(1)t;(2)小于;(3)6时;(4)3;(5)后面;(6)9;4.5.
21.解:(1)∵△ABC是等边三角形,∴∠ACB=60°,
∵CE=CD,∴∠E=∠CDE,
∵∠ACB=∠E+∠CDE,∴∠ACB=2∠E,
∴∠E=60°÷2=30°.即∠E的度数是30°.
(2)如图,连接BD,,
∵△ABC是等边三角形,D是AC的中点,
∴BD是∠ABC的平分线,∴∠ABC=2∠DBE;
∵CE=CD,∴∠CED=∠CDE.
∵∠ACB=∠E+∠CDE,∴∠ACB=2∠E;
∵∠ABC=∠ACB,∴2∠DBC=2∠E,
∴∠DBC=∠E,∴BD=DE,
∵DM⊥BE,∴BM=EM.
22.解:(1)如图1,∵△ABC是等边三角形,∴∠BAC=∠ACB=60°.
又∵∠BAD+∠DAC=∠BAC,∠EDC+∠DEC=∠ACB,
∴∠BAD+∠DAC=∠EDC+∠DEC.
∵DE=DA,∴∠DAC=∠DEC,∴∠BAD=∠EDC.
(2)猜想:DM=AM.理由如下:
∵点M、E关于直线BC对称,∴∠MDC=∠EDC,DE=DM.
又由(1)知∠BAD=∠EDC,∴∠MDC=∠BAD.
∵∠ADC=∠BAD+∠B,即∠ADM+∠MDC=∠BAD+∠B,∴∠ADM=∠B=60°.
又∵DA=DE=DM,
∴△ADM是等边三角形, ∴DM=AM.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 11 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
北师大七年级下学期阶段诊断卷(五)
考试范围:第1—5单元;考试时间:100分钟
一.选择题(每题3分,共30分)
1.下列图形中不是轴对称图形的是( )
A B C D
2.下列四句话的文字有三句具有对称规律,其中没有这种规律的一句是( )
A.有志者事竟成 B.上海自来水来自海上
C.清水池里池水清 D.蜜蜂酿蜂蜜
3.若m、n均为正整数且,,则的值为( )
A.10 B.11 C.12 D.13
4.已知△ABC的三边长分别为4、4、6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )条.
A.3 B.4 C.5 D.6
5.如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA、BC于点G、H;再分别以点G、H为圆心,大于GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.若∠A=100°,则∠EBC度数为( )
A.50° B.40° C.30° D.80°
6.若的展开式中不含x的一次项,则a的值是( )
A. B.2 C. D.任意数
7.根据下列已知条件,能画出唯一的△ABC的是( )
A.AB=3,BC=4,∠C=50° B.AB=4,BC=3,∠A=30°
C.∠C=90°,AB=6 D.∠A=60°,∠B=45°,AB=4
8.如图,△ABC与△A′B′C′关于直线MN对称,P为MN上任一点(P不与AA′共线),下列结论中错误的是( )
A.△AA′P是等腰三角形
B.MN垂直平分AA′、CC′
C.△ABC与△A′B′C′面积相等
D.直线AB、A′B′的交点不一定在MN上
9.如图,四边形ABCD中,AB=AD,点B关于AC的对称点B′恰好落在CD上,若∠BAD=100°,则∠ACB的度数为( )
A.40° B.45° C.60° D.80°
10.如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC、AB边于E、F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
A.6 B.8 C.10 D.12
二.填空题(每题3分,共15分)
11.小明在平面镜里看到背后墙上电子钟显示的时间如图所示,此刻的实际时间应该是_____________.
12.如图所示,AB∥CE,∠C=35°,∠A=115°,那么∠F=_________°.
13.如图,在5×2方格纸中,有一个以格点为顶点的△ABC,请你找出方格纸中所有与△ABC成轴对称且以格点为顶点的三角形,这样的三角形共有____________个.
14.若,,则M与N的大小关系为_______________.
15.如图,是小明从学校到家里行进的路程s(米)与时间t(分)的图象.观察图象,从中得到如下信息:
①学校离小明家1000米;
②小明用了20分钟到家;
③小明前10分钟走了路程的一半;
④小明后10分钟比前10分钟走得快,
其中正确的有___________________(填序号).
三.解答题(共55分)
16.(8分)化简求值:已知,求代数式的值.
17.(6分)如图,在正方形网格上有一个△DEF.
(1)作△DEF关于直线HG的轴对称图形△ABC(不写作法);
(2)作EF边上的高(不写作法);
(3)若网格上的最小正方形边长为1,求△DEF的面积.
18.(7分)如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD∥BC.
19.(7分)如图,在△ABC中,点O是∠ABC、∠ACB平分线的交点,AB+BC+AC=20,过O作OD⊥BC于D点,且OD=3,求△ABC的面积.
20.(7分)如图是甲、乙两人从同一地点出发后,路程随时间变化的图象.
(1)在此变化过程中,______________是自变量;
(2)甲的速度_________乙的速度;(填“大于”、“等于”、或“小于”)
(3)甲出发后___________与乙相遇;
(4)甲比乙先走__________小时;
(5)9时甲在乙的___________(填“前面”、“后面”、“相同位置”);
(6)路程为150千米,甲行驶了____________小时,乙行驶了____________小时.
21.(10分)已知,如图,△ABC是等边三角形,点D是AC的中点,延长BC到E,使CE=CD,连接DE,过点D作DM⊥BE于M.
(1)求∠E的度数.
(2)求证:BM=EM.
22.(10分)如图,在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA.
(1)求证:∠BAD=∠EDC;
(2)作出点E关于直线BC的对称点M,连接DM、AM,猜想DM与AM的数量关系,并说明理由.
参考答案
一.选择题(共10小题,每题3分,共30分)
A.A.B.B.B. A.D.D.A.C.
二.填空题(共5小题)
11.21:05.
12.80.
13.4.
14.M>N.
15.①,②,④.
三.解答题(共7小题,共55分)
16.解:∵|a|+(b+3)2=0,
∴a0,b﹣3=0, ∴a,b=3,
[(2a+b)2+(2a+b)(b﹣2a)﹣6b]÷2b,
=(4a2+b2+4ab+b2﹣4a2﹣6b)÷2b,=b+2a﹣3,
把a,b=3代入得:原式=b+2a﹣3=3+2×()﹣3=﹣1;
17.解:(1)所作图形如图所示:
△ABC即为所作图形;
(2)所作图形如图所示:
DM即为EF边上的高;
(3)S△DEF3×2=3.
18.证明:∵AE平分∠BAD, ∴∠1=∠2,
∵AB∥CD,∠CFE=∠E, ∴∠1=∠CFE=∠E,
∴∠2=∠E, ∴AD∥BC.
19.解:如图,过点O作OE⊥AB于E,OF⊥AC于F,连接OA.
∵点O是∠ABC,∠ACB平分线的交点,∴OE=OD,OF=OD,即OE=OF=OD=3,
∴S△ABC=S△ABO+S△BCO+S△ACOAB OEBC ODAC OF
2×(AB+BC+AC)3×20=30.
20.解:(1)函数图象反映路程随时间变化的图象,则t是自变量,s为因变量;
(2)甲的速度千米/小时,所以甲的速度小于乙的速度;
(3)6时表示他们相遇,即乙追赶上了甲;
(4)甲比乙先走3小时;
(5)t=9时,乙的图象在甲的上方,即乙行驶的路程远些,所以9时甲在乙的后面;
(6)路程为150千米,甲行驶了9时,乙行驶的时间为:150÷(100÷3)=4.5(小时).
故答案为:(1)t;(2)小于;(3)6时;(4)3;(5)后面;(6)9;4.5.
21.解:(1)∵△ABC是等边三角形,∴∠ACB=60°,
∵CE=CD,∴∠E=∠CDE,
∵∠ACB=∠E+∠CDE,∴∠ACB=2∠E,
∴∠E=60°÷2=30°.即∠E的度数是30°.
(2)如图,连接BD,,
∵△ABC是等边三角形,D是AC的中点,
∴BD是∠ABC的平分线,∴∠ABC=2∠DBE;
∵CE=CD,∴∠CED=∠CDE.
∵∠ACB=∠E+∠CDE,∴∠ACB=2∠E;
∵∠ABC=∠ACB,∴2∠DBC=2∠E,
∴∠DBC=∠E,∴BD=DE,
∵DM⊥BE,∴BM=EM.
22.解:(1)如图1,∵△ABC是等边三角形,∴∠BAC=∠ACB=60°.
又∵∠BAD+∠DAC=∠BAC,∠EDC+∠DEC=∠ACB,
∴∠BAD+∠DAC=∠EDC+∠DEC.
∵DE=DA,∴∠DAC=∠DEC,∴∠BAD=∠EDC.
(2)猜想:DM=AM.理由如下:
∵点M、E关于直线BC对称,∴∠MDC=∠EDC,DE=DM.
又由(1)知∠BAD=∠EDC,∴∠MDC=∠BAD.
∵∠ADC=∠BAD+∠B,即∠ADM+∠MDC=∠BAD+∠B,∴∠ADM=∠B=60°.
又∵DA=DE=DM,
∴△ADM是等边三角形, ∴DM=AM.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 11 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
