青岛版九年级数学下册 5.2 反比例函数(第2课时)课件(共16张)
文档属性
| 名称 | 青岛版九年级数学下册 5.2 反比例函数(第2课时)课件(共16张) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-17 14:00:17 | ||
图片预览


文档简介
(共19张PPT)
5.2 反比例函数(2)
------反比例函数的图象及性质
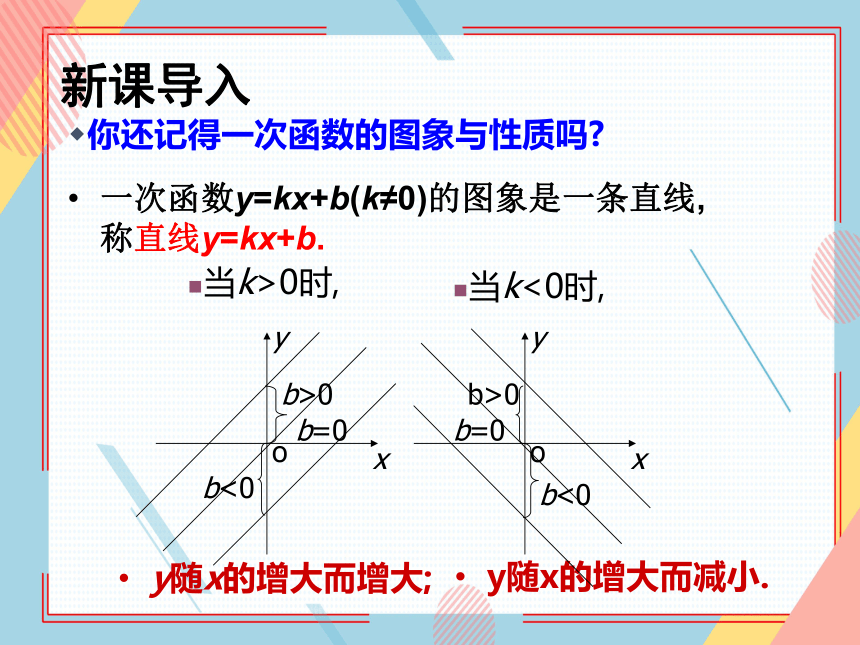
你还记得一次函数的图象与性质吗
一次函数y=kx+b(k≠0)的图象是一条直线,称直线y=kx+b.
y随x的增大而增大;
x
y
o
x
y
o
y随x的增大而减小.
b<0
b>0
b=0
b<0
b>0
b=0
当k>0时,
当k<0时,
新课导入
1.会画反例函数的图象;
2.能根据图象和表达式探索并理解反比例函数的性质。
学习目标
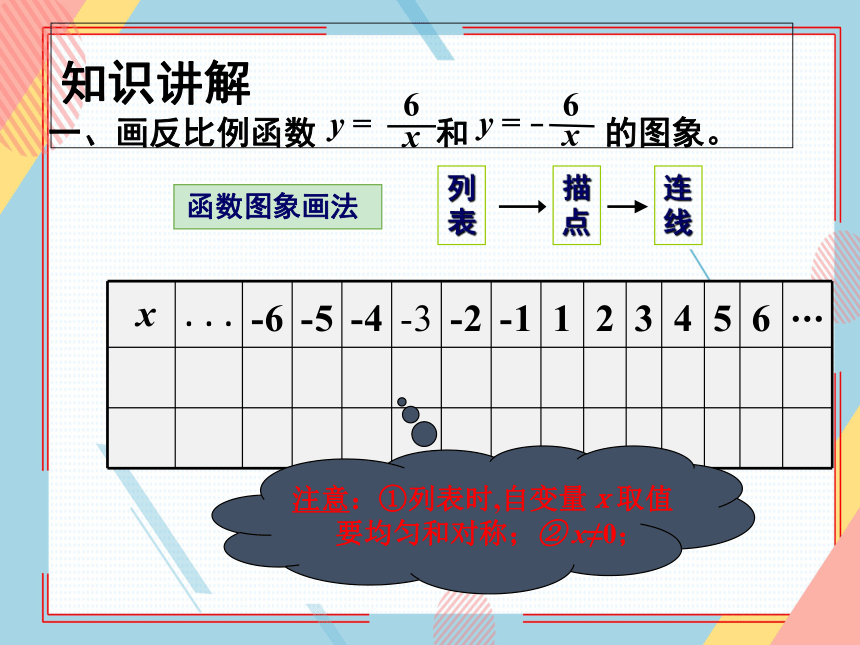
一、画反比例函数 和 的图象。
y =
x
6
y =
x
6
函数图象画法
列
表
描
点
连
线
x ... -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 ...
注意:①列表时,自变量x取值
要均匀和对称;② x≠0;
知识讲解
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
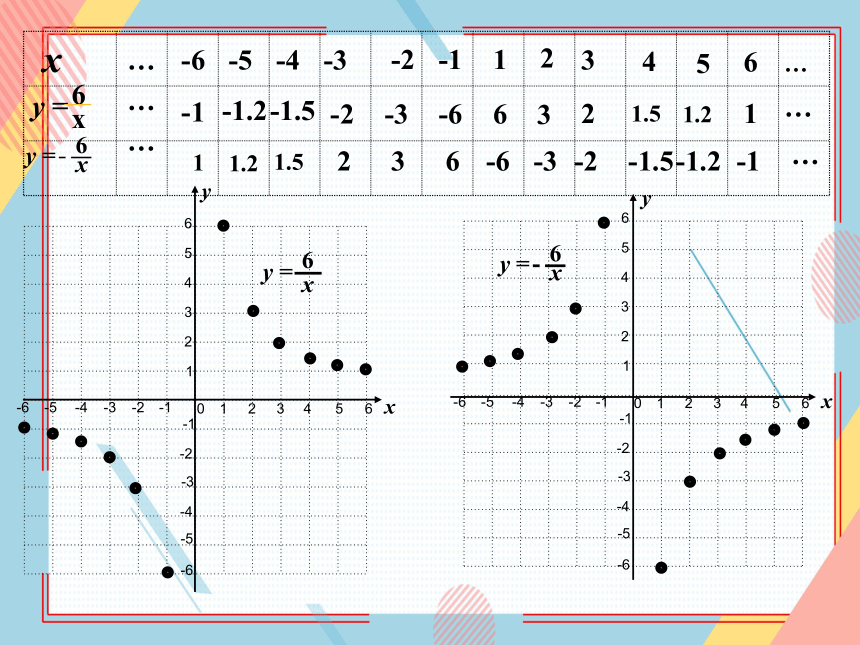
x
y
1
6
2
3
3
2
4
1.5
5
1.2
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y =
x
6
y =
x
6
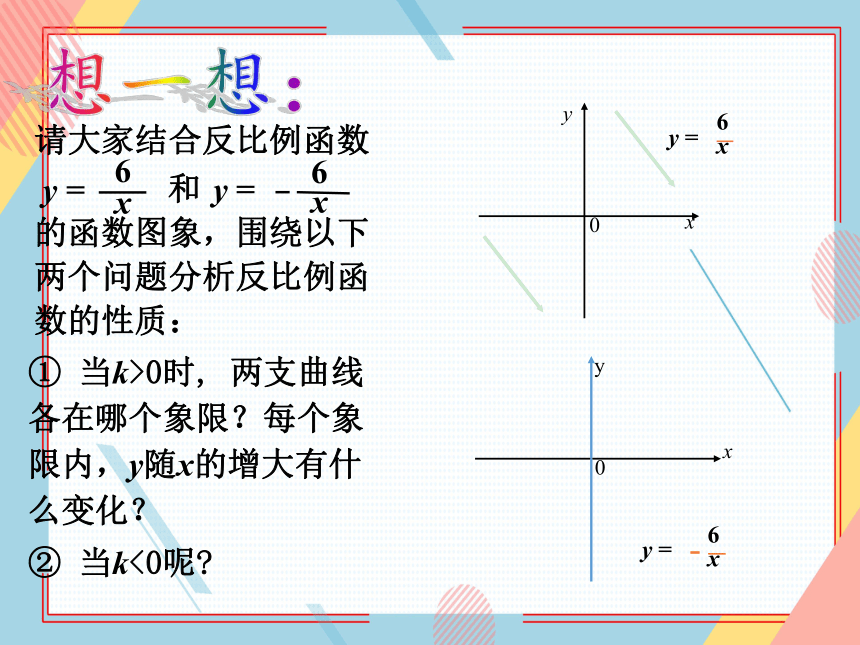
① 当k>0时, 两支曲线各在哪个象限?每个象限内,y随x的增大有什么变化?
② 当k<0呢
请大家结合反比例函数
和 的函数图象,围绕以下两个问题分析反比例函数的性质:
y =
x
6
y =
x
6
y =
x
6
x
y
0
y
x
x
6
y =
0
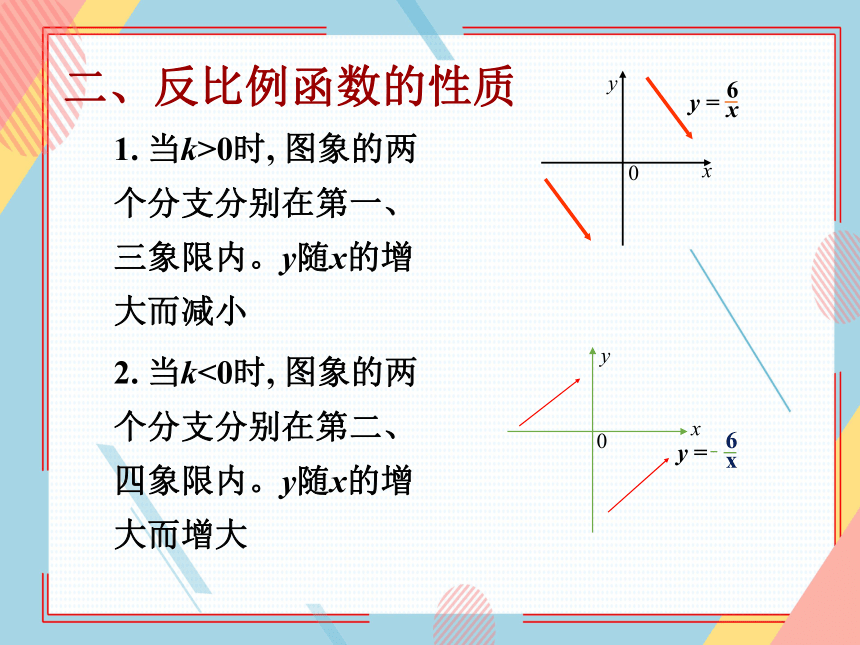
二、反比例函数的性质
1. 当k>0时, 图象的两个分支分别在第一、三象限内。y随x的增大而减小
2. 当k<0时, 图象的两个分支分别在第二、四象限内。y随x的增大而增大
y =
x
6
x
y
0
y
x
x
6
y =
0
(1)如果反比例函数y=k/x的图象过点(3,-4), 那么函数的图象应在( )
A.第一、三象限 B.第一、第二象限
C.第二、四象限 D.第三、四象限
(2)当x<0时,函数y=x与y=1/x在同一坐标系中的图象在大致是( )
X
Y
A
X
Y
B
X
Y
C
X
Y
D
小试牛刀
(3)反比例函数y=k/x(k≠0),当k>0时,函数的图象的两个分支分别应在( )
A.第一、第三象限 B.第一、第二象限
C.第二、四象限 D.第三、四象限
(4)反比例函数y=-4/x的图象大致是( )
X
Y
A
X
Y
B
X
Y
C
X
Y
D
三、典型例题:
知识讲解
方法一.特殊值法
不妨设: 代入 得,
方法二.分析法
因为k=-3<0,根据性质可知图象的两个分支分别在第二、四象限内,并且在每个象限内,y随x的增大而增大,在第二象限内的函数值为正的,第四象限的函数值为负的。
方法三.图像法
三、典型例题:
解析:显然将p1,p2分别代入各自双曲线得,
K1=2b1,K2=2b2,因b1所以:K1知识讲解
随堂练习
一、反比例函数 有下列性质:
1.反比例函数的图象 是由两支曲线组成的。
因此称反比例函数的图象为双曲线.
2.(1)当 k>0 时,两支曲线分别位于第一、三象限,
y随x的增大而减小.
(2)当 k<0 时,两支曲线分别位于第二、四象限, y随x的增大而增大.
二、函数值大小的比较方法
本课小结
三、正反比例函数对照表
5.2 反比例函数(2)
------反比例函数的图象及性质
你还记得一次函数的图象与性质吗
一次函数y=kx+b(k≠0)的图象是一条直线,称直线y=kx+b.
y随x的增大而增大;
x
y
o
x
y
o
y随x的增大而减小.
b<0
b>0
b=0
b<0
b>0
b=0
当k>0时,
当k<0时,
新课导入
1.会画反例函数的图象;
2.能根据图象和表达式探索并理解反比例函数的性质。
学习目标
一、画反比例函数 和 的图象。
y =
x
6
y =
x
6
函数图象画法
列
表
描
点
连
线
x ... -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 ...
注意:①列表时,自变量x取值
要均匀和对称;② x≠0;
知识讲解
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y =
x
6
y =
x
6
① 当k>0时, 两支曲线各在哪个象限?每个象限内,y随x的增大有什么变化?
② 当k<0呢
请大家结合反比例函数
和 的函数图象,围绕以下两个问题分析反比例函数的性质:
y =
x
6
y =
x
6
y =
x
6
x
y
0
y
x
x
6
y =
0
二、反比例函数的性质
1. 当k>0时, 图象的两个分支分别在第一、三象限内。y随x的增大而减小
2. 当k<0时, 图象的两个分支分别在第二、四象限内。y随x的增大而增大
y =
x
6
x
y
0
y
x
x
6
y =
0
(1)如果反比例函数y=k/x的图象过点(3,-4), 那么函数的图象应在( )
A.第一、三象限 B.第一、第二象限
C.第二、四象限 D.第三、四象限
(2)当x<0时,函数y=x与y=1/x在同一坐标系中的图象在大致是( )
X
Y
A
X
Y
B
X
Y
C
X
Y
D
小试牛刀
(3)反比例函数y=k/x(k≠0),当k>0时,函数的图象的两个分支分别应在( )
A.第一、第三象限 B.第一、第二象限
C.第二、四象限 D.第三、四象限
(4)反比例函数y=-4/x的图象大致是( )
X
Y
A
X
Y
B
X
Y
C
X
Y
D
三、典型例题:
知识讲解
方法一.特殊值法
不妨设: 代入 得,
方法二.分析法
因为k=-3<0,根据性质可知图象的两个分支分别在第二、四象限内,并且在每个象限内,y随x的增大而增大,在第二象限内的函数值为正的,第四象限的函数值为负的。
方法三.图像法
三、典型例题:
解析:显然将p1,p2分别代入各自双曲线得,
K1=2b1,K2=2b2,因b1
随堂练习
一、反比例函数 有下列性质:
1.反比例函数的图象 是由两支曲线组成的。
因此称反比例函数的图象为双曲线.
2.(1)当 k>0 时,两支曲线分别位于第一、三象限,
y随x的增大而减小.
(2)当 k<0 时,两支曲线分别位于第二、四象限, y随x的增大而增大.
二、函数值大小的比较方法
本课小结
三、正反比例函数对照表
