湘教版数学七年级下册 4.1.2 相交直线所成的角 课件(共23张PPT)
文档属性
| 名称 | 湘教版数学七年级下册 4.1.2 相交直线所成的角 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-17 14:15:03 | ||
图片预览







文档简介
(共26张PPT)
第4章 相交线与平行线
4.1.2 相交直线所成的角
学习目标
1.理解对顶角、同位角、内错角、同旁内角的概念;
2.掌握对顶角的性质,并能运用它的性质进行角的运算及一
些实际问题.(重点、难点)
观察下列图片,试猜想两条相交直线所成的角有什么关系?
情境引入
问题 剪刀剪东西的过程中,∠AOC和∠BOD这两个角的位置保持怎样的关系?
A
O
C
B
D
∠AOC和∠BOD有公共顶点,且∠AOC的两边分别是∠BOD两边的反向延长线.
对顶角的概念
一
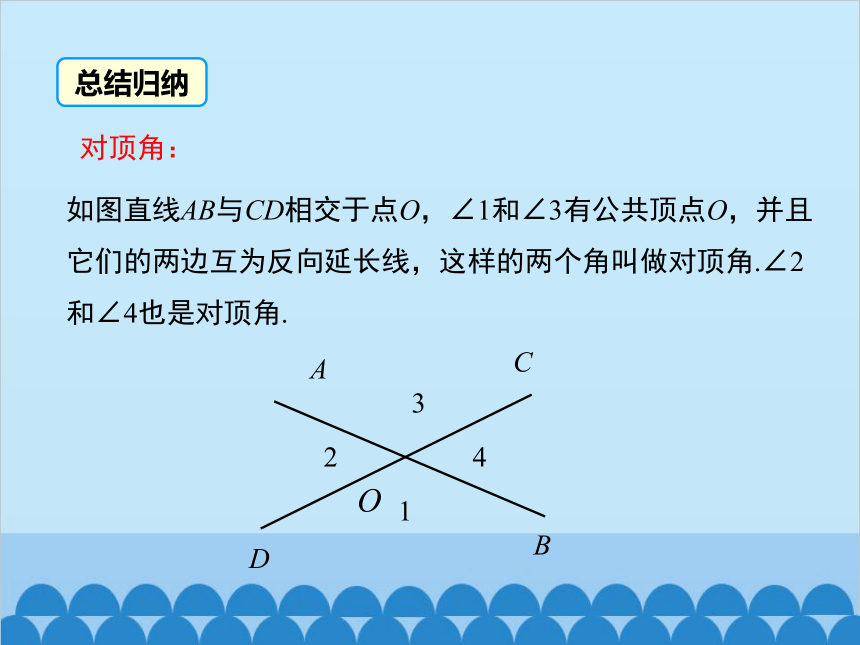
如图直线AB与CD相交于点O,∠1和∠3有公共顶点O,并且它们的两边互为反向延长线,这样的两个角叫做对顶角.∠2和∠4也是对顶角.
对顶角:
A
O
C
B
D
1
3
2
4
总结归纳
判断下列各图中∠1和∠2是否为对顶角,并说明理由?
1
2
1
2
1
2
1
2
1
2
1
2
√
×
×
×
×
×
练一练
请你猜一猜,剪刀剪东西的过程中,∠AOC和∠BOD这两个角的大小保持怎样的关系?
对顶角的性质
二
A
O
C
B
D
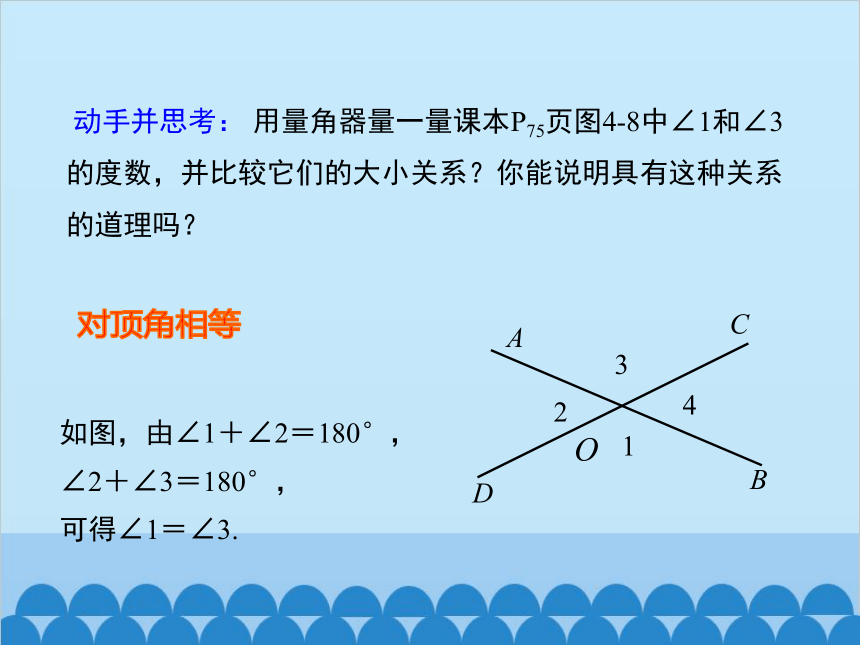
动手并思考: 用量角器量一量课本P75页图4-8中∠1和∠3的度数,并比较它们的大小关系?你能说明具有这种关系的道理吗?
如图,由∠1+∠2=180°,
∠2+∠3=180°,
可得∠1=∠3.
A
O
C
B
D
1
3
2
4
例1 如图,两条直线相交所形成的四个角中,已知 ∠1=30°,那么∠2、∠3和∠4各等于多少度
解: ∵ ∠1 与∠2互补,(已知)
∴ ∠2=180°-∠1=180°-30°=150°. (互补的定义)
∵ ∠1与∠3, ∠2与∠4分别是对顶角,(已知)
∴ ∠3=∠1=30°, (对顶角相等)
∠4=∠2=150°. (对顶角相等)
典例精析
6
7
5
8
B
C
A
F
E
D
4
3
1
2
O
同位角、内错角、同旁内角
三
如图,直线AB、CD与EF相交,我们就称为直线AB、CD被直线EF所截.三条直线相交构成如图的8个角.其中AB、CD叫做被截线,EF叫做截线.
F
活动1 观察∠1与∠5的位置关系:
①在直线EF的同旁(右边)
②在直线AB、CD的同一侧(上方)
A
C
B
D
E
1
2
3
4
5
6
7
8
1
5
∠2和∠6;∠3和∠7;∠4和∠8
图中的同位角还有哪些?
同位角
图形特征:在形如字母“F”的图形中有同位角.
变式图形:图中的∠1与∠2都是同位角.
1
2
1
2
1
2
1
2
A
C
B
D
E
F
1
2
3
4
5
6
7
8
活动2 观察∠3与∠5的位置关系:
①在直线EF的两侧
②在直线AB、CD的之间
3
5
∠4和∠6
图中的内错角还有哪些?
内错角
变式图形:图中的∠1与∠2都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
A
C
B
D
E
F
1
2
3
4
5
6
7
8
活动3 观察∠4与∠5的位置关系
①在直线EF的同旁
②在直线AB、CD的之间
4
5
∠3和∠6
图中还有哪些同旁内角?
图形特征:在形如“U”的图形中有同旁内角.
同旁内角
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
截线 被截线 结构
特征
同位角
内错角
同旁内角
之间
之间
同侧
同旁
两旁
同旁
F
Z
U
总结归纳
例2 如图,直线DE截AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角.
解:两条直线是AB,AC,截线是DE,所以8个角中,同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6和∠3;内错角:∠4与∠5,∠1与∠6,;同旁内角:∠1与∠5,∠4与∠6.
变式:∠A与∠8是哪两条直线被第哪条直线所截的角 它们是什么关系的角 ∠A与∠5呢 ∠A与∠6呢
E
D
C
B
A
8
7
6
5
4
3
2
1
典例精析
1.下列说法中,正确的有( )
①对顶角相等
②相等的角是对顶角
③不是对顶角的两个角就不相等
④不相等的角不是对顶角
A.1个 B.2个 C.3个 D.0个
B
2.如图,∠DAB和∠ABC是 ( )
A.同位角 B.同旁内角
C.内错角 D.以上结论都不对
3.如图,∠1和∠2不能构成同位角的图形是 ( )
C
D
A
D
B
C
E
3.要测量两堵墙所成的角的度数,但人不能进入围墙,如何测量?
A
B
O
C
D
两个角有公共顶点,且一个角的两边分别是另一个角两边的反向延长线,这样的两个角叫做对顶角.
对顶角性质:对顶角相等.
同位角、内错角、同旁内角的结构特征:
三线八角
同位角 “F”型
内错角 “Z”型
同旁内角 “U”型
第4章 相交线与平行线
4.1.2 相交直线所成的角
学习目标
1.理解对顶角、同位角、内错角、同旁内角的概念;
2.掌握对顶角的性质,并能运用它的性质进行角的运算及一
些实际问题.(重点、难点)
观察下列图片,试猜想两条相交直线所成的角有什么关系?
情境引入
问题 剪刀剪东西的过程中,∠AOC和∠BOD这两个角的位置保持怎样的关系?
A
O
C
B
D
∠AOC和∠BOD有公共顶点,且∠AOC的两边分别是∠BOD两边的反向延长线.
对顶角的概念
一
如图直线AB与CD相交于点O,∠1和∠3有公共顶点O,并且它们的两边互为反向延长线,这样的两个角叫做对顶角.∠2和∠4也是对顶角.
对顶角:
A
O
C
B
D
1
3
2
4
总结归纳
判断下列各图中∠1和∠2是否为对顶角,并说明理由?
1
2
1
2
1
2
1
2
1
2
1
2
√
×
×
×
×
×
练一练
请你猜一猜,剪刀剪东西的过程中,∠AOC和∠BOD这两个角的大小保持怎样的关系?
对顶角的性质
二
A
O
C
B
D
动手并思考: 用量角器量一量课本P75页图4-8中∠1和∠3的度数,并比较它们的大小关系?你能说明具有这种关系的道理吗?
如图,由∠1+∠2=180°,
∠2+∠3=180°,
可得∠1=∠3.
A
O
C
B
D
1
3
2
4
例1 如图,两条直线相交所形成的四个角中,已知 ∠1=30°,那么∠2、∠3和∠4各等于多少度
解: ∵ ∠1 与∠2互补,(已知)
∴ ∠2=180°-∠1=180°-30°=150°. (互补的定义)
∵ ∠1与∠3, ∠2与∠4分别是对顶角,(已知)
∴ ∠3=∠1=30°, (对顶角相等)
∠4=∠2=150°. (对顶角相等)
典例精析
6
7
5
8
B
C
A
F
E
D
4
3
1
2
O
同位角、内错角、同旁内角
三
如图,直线AB、CD与EF相交,我们就称为直线AB、CD被直线EF所截.三条直线相交构成如图的8个角.其中AB、CD叫做被截线,EF叫做截线.
F
活动1 观察∠1与∠5的位置关系:
①在直线EF的同旁(右边)
②在直线AB、CD的同一侧(上方)
A
C
B
D
E
1
2
3
4
5
6
7
8
1
5
∠2和∠6;∠3和∠7;∠4和∠8
图中的同位角还有哪些?
同位角
图形特征:在形如字母“F”的图形中有同位角.
变式图形:图中的∠1与∠2都是同位角.
1
2
1
2
1
2
1
2
A
C
B
D
E
F
1
2
3
4
5
6
7
8
活动2 观察∠3与∠5的位置关系:
①在直线EF的两侧
②在直线AB、CD的之间
3
5
∠4和∠6
图中的内错角还有哪些?
内错角
变式图形:图中的∠1与∠2都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
A
C
B
D
E
F
1
2
3
4
5
6
7
8
活动3 观察∠4与∠5的位置关系
①在直线EF的同旁
②在直线AB、CD的之间
4
5
∠3和∠6
图中还有哪些同旁内角?
图形特征:在形如“U”的图形中有同旁内角.
同旁内角
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
截线 被截线 结构
特征
同位角
内错角
同旁内角
之间
之间
同侧
同旁
两旁
同旁
F
Z
U
总结归纳
例2 如图,直线DE截AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角.
解:两条直线是AB,AC,截线是DE,所以8个角中,同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6和∠3;内错角:∠4与∠5,∠1与∠6,;同旁内角:∠1与∠5,∠4与∠6.
变式:∠A与∠8是哪两条直线被第哪条直线所截的角 它们是什么关系的角 ∠A与∠5呢 ∠A与∠6呢
E
D
C
B
A
8
7
6
5
4
3
2
1
典例精析
1.下列说法中,正确的有( )
①对顶角相等
②相等的角是对顶角
③不是对顶角的两个角就不相等
④不相等的角不是对顶角
A.1个 B.2个 C.3个 D.0个
B
2.如图,∠DAB和∠ABC是 ( )
A.同位角 B.同旁内角
C.内错角 D.以上结论都不对
3.如图,∠1和∠2不能构成同位角的图形是 ( )
C
D
A
D
B
C
E
3.要测量两堵墙所成的角的度数,但人不能进入围墙,如何测量?
A
B
O
C
D
两个角有公共顶点,且一个角的两边分别是另一个角两边的反向延长线,这样的两个角叫做对顶角.
对顶角性质:对顶角相等.
同位角、内错角、同旁内角的结构特征:
三线八角
同位角 “F”型
内错角 “Z”型
同旁内角 “U”型
