华东师大版数学九年级下册 专题课堂 垂径定理与圆周角的应用 课件 (共20张PPT)
文档属性
| 名称 | 华东师大版数学九年级下册 专题课堂 垂径定理与圆周角的应用 课件 (共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 413.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-17 16:13:28 | ||
图片预览




文档简介
(共21张PPT)
数学 九年级下册 华师版
第27章 圆
专题课堂(五) 垂径定理与圆周角的应用
一、垂径定理的运用
类型一:求圆的圆心
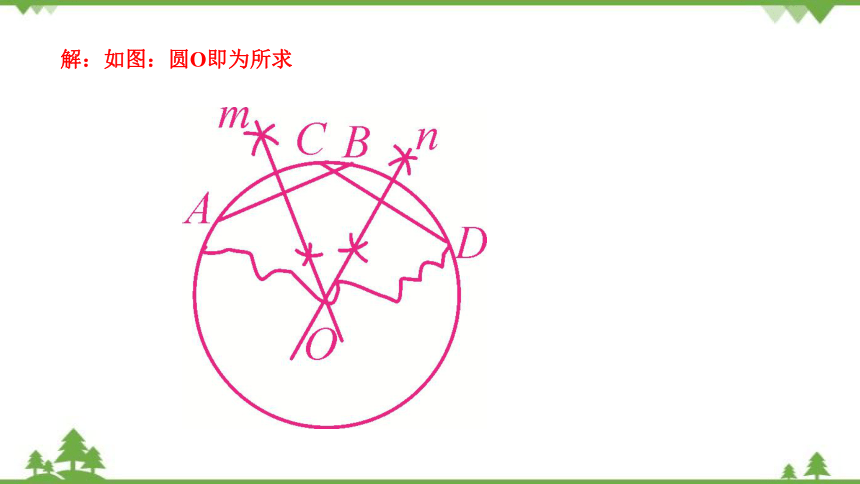
【例1】如图是破残的圆形轮片,求作此残片所在的圆.(不写作法,保留作图痕迹)
分析:根据圆的性质,弦的垂直平分线过圆心,所以只要找到两个弦的垂直平分线,相交点即为圆心,有圆心就可以作出残片所在的圆.
解:如图:圆O即为所求
[对应训练]
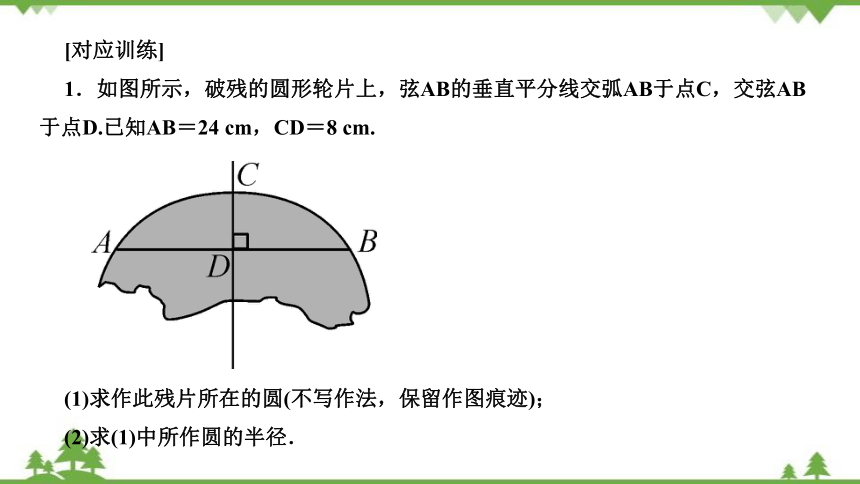
1.如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知AB=24 cm,CD=8 cm.
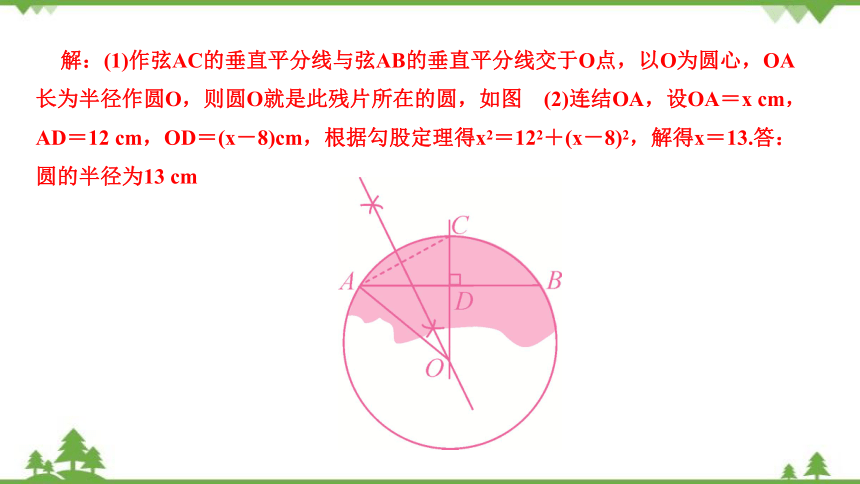
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)求(1)中所作圆的半径.
解:(1)作弦AC的垂直平分线与弦AB的垂直平分线交于O点,以O为圆心,OA长为半径作圆O,则圆O就是此残片所在的圆,如图 (2)连结OA,设OA=x cm,AD=12 cm,OD=(x-8)cm,根据勾股定理得x2=122+(x-8)2,解得x=13.答:圆的半径为13 cm
类型二:求线段的长
【例2】(滨州中考)在⊙O中,直径AB=15,弦DE⊥AB于点C,若OC∶OB=3∶5,则DE的长为( )
A.6 B.9 C.12 D.15
【分析】直接根据题意画出图形,再利用垂径定理以及勾股定理得出答案.
C
[对应训练]
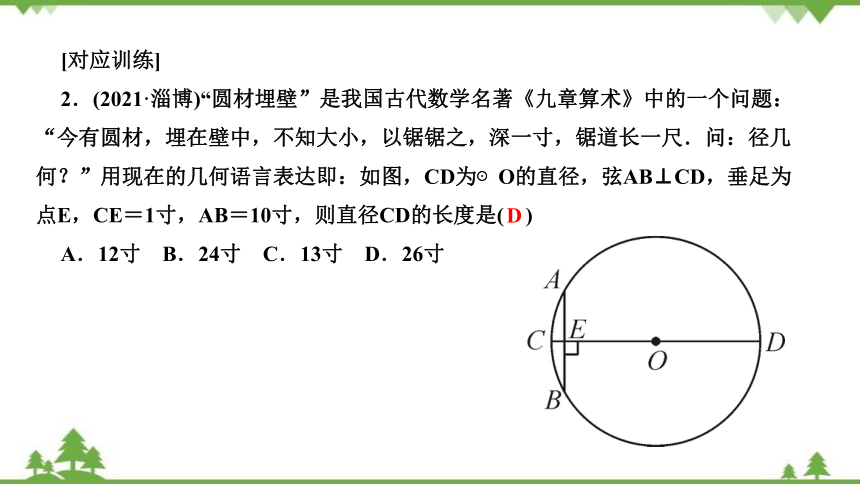
2.(2021·淄博)“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?”用现在的几何语言表达即:如图,CD为⊙O的直径,弦AB⊥CD,垂足为点E,CE=1寸,AB=10寸,则直径CD的长度是( )
A.12寸 B.24寸 C.13寸 D.26寸
D
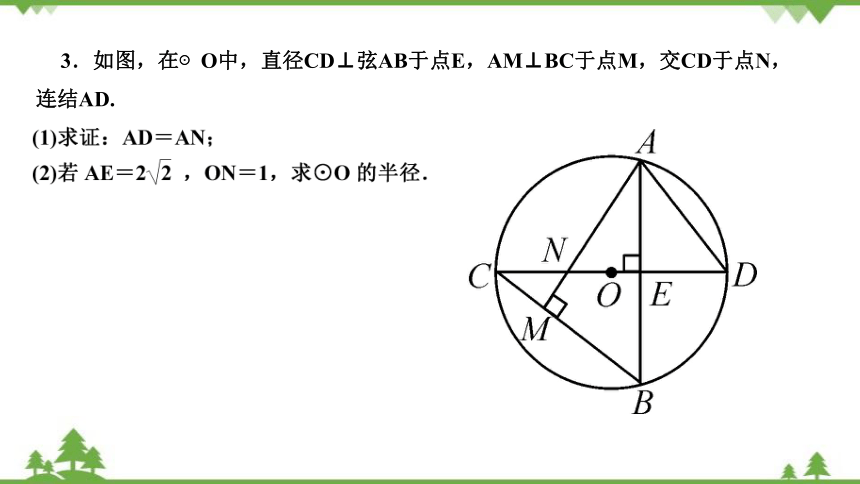
3.如图,在⊙O中,直径CD⊥弦AB于点E,AM⊥BC于点M,交CD于点N,连结AD.
解:(1)∵∠BAD与∠BCD是同弧所对的圆周角∴∠BAD∠BCD.∵AE⊥CD,AM⊥BC,∴∠AMC=∠AEN=90°.∵∠ANE=∠CNM,∴∠BCD=∠BAM,∴∠BAM=∠BAD.又∵AE=AE,∠AEN=∠AED,∴△ANE≌△ADE,∴AD=AN
二、圆周角定理与三角形的综合运用
类型一:圆周角定理与直角三角形的综合运用
【例3】(扬州中考)如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则sin ∠ADC的值为( )
A
【分析】首先根据圆周角定理可知,∠ADC=∠ABC,然后在Rt△ACB中,根据锐角三角函数的定义求出∠ABC的正弦值.
[对应训练]
4.(2021·宜昌)如图,C,D是⊙O上直径AB两侧的两点,设∠ABC=25°,则∠BDC=( )
A.85° B.75° C.70° D.65°
D
5.(黔东南州中考)如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB=30°,则点O到CD的距离OE为____.
类型二:圆周角定理与等腰三角形的综合运用
【例4】(杭州中考)如图,AB是⊙O的直径,点C是半径OA的中点,过点C作DE⊥AB,交⊙O于D,E两点,过点D作直径DF,连结AF,则∠DFA=_____.
分析:利用垂径定理和三角函数得出∠CDO的度数,进而得出∠DOA的度数,利用圆周角定理得出∠DFA的度数即可.
30°
C
13°
9.(2021·徐州)如图,AB为⊙O的直径,点C,D在⊙O上,AC与OD交于点E,AE=EC,OE=ED.连结BC,CD.求证:
(1)△AOE≌△CDE;
(2)四边形OBCD是菱形.
(2)连结OC,如图,∵AE=CE,∴OD⊥AC,∵OE=DE,∴CE垂直平分OD,∴CD=CO,∴△OCD为等边三角形,∴∠COD=60°,∵AB为直径,∴∠ACB=90°,∴BC∥OD,∴∠BCO=∠COD=60°,而OB=OC,∴△OCB为等边三角形,∴BC=OC,∴OB=BC=CD=OD,∴四边形OBCD是菱形
数学 九年级下册 华师版
第27章 圆
专题课堂(五) 垂径定理与圆周角的应用
一、垂径定理的运用
类型一:求圆的圆心
【例1】如图是破残的圆形轮片,求作此残片所在的圆.(不写作法,保留作图痕迹)
分析:根据圆的性质,弦的垂直平分线过圆心,所以只要找到两个弦的垂直平分线,相交点即为圆心,有圆心就可以作出残片所在的圆.
解:如图:圆O即为所求
[对应训练]
1.如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知AB=24 cm,CD=8 cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)求(1)中所作圆的半径.
解:(1)作弦AC的垂直平分线与弦AB的垂直平分线交于O点,以O为圆心,OA长为半径作圆O,则圆O就是此残片所在的圆,如图 (2)连结OA,设OA=x cm,AD=12 cm,OD=(x-8)cm,根据勾股定理得x2=122+(x-8)2,解得x=13.答:圆的半径为13 cm
类型二:求线段的长
【例2】(滨州中考)在⊙O中,直径AB=15,弦DE⊥AB于点C,若OC∶OB=3∶5,则DE的长为( )
A.6 B.9 C.12 D.15
【分析】直接根据题意画出图形,再利用垂径定理以及勾股定理得出答案.
C
[对应训练]
2.(2021·淄博)“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?”用现在的几何语言表达即:如图,CD为⊙O的直径,弦AB⊥CD,垂足为点E,CE=1寸,AB=10寸,则直径CD的长度是( )
A.12寸 B.24寸 C.13寸 D.26寸
D
3.如图,在⊙O中,直径CD⊥弦AB于点E,AM⊥BC于点M,交CD于点N,连结AD.
解:(1)∵∠BAD与∠BCD是同弧所对的圆周角∴∠BAD∠BCD.∵AE⊥CD,AM⊥BC,∴∠AMC=∠AEN=90°.∵∠ANE=∠CNM,∴∠BCD=∠BAM,∴∠BAM=∠BAD.又∵AE=AE,∠AEN=∠AED,∴△ANE≌△ADE,∴AD=AN
二、圆周角定理与三角形的综合运用
类型一:圆周角定理与直角三角形的综合运用
【例3】(扬州中考)如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则sin ∠ADC的值为( )
A
【分析】首先根据圆周角定理可知,∠ADC=∠ABC,然后在Rt△ACB中,根据锐角三角函数的定义求出∠ABC的正弦值.
[对应训练]
4.(2021·宜昌)如图,C,D是⊙O上直径AB两侧的两点,设∠ABC=25°,则∠BDC=( )
A.85° B.75° C.70° D.65°
D
5.(黔东南州中考)如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB=30°,则点O到CD的距离OE为____.
类型二:圆周角定理与等腰三角形的综合运用
【例4】(杭州中考)如图,AB是⊙O的直径,点C是半径OA的中点,过点C作DE⊥AB,交⊙O于D,E两点,过点D作直径DF,连结AF,则∠DFA=_____.
分析:利用垂径定理和三角函数得出∠CDO的度数,进而得出∠DOA的度数,利用圆周角定理得出∠DFA的度数即可.
30°
C
13°
9.(2021·徐州)如图,AB为⊙O的直径,点C,D在⊙O上,AC与OD交于点E,AE=EC,OE=ED.连结BC,CD.求证:
(1)△AOE≌△CDE;
(2)四边形OBCD是菱形.
(2)连结OC,如图,∵AE=CE,∴OD⊥AC,∵OE=DE,∴CE垂直平分OD,∴CD=CO,∴△OCD为等边三角形,∴∠COD=60°,∵AB为直径,∴∠ACB=90°,∴BC∥OD,∴∠BCO=∠COD=60°,而OB=OC,∴△OCB为等边三角形,∴BC=OC,∴OB=BC=CD=OD,∴四边形OBCD是菱形
