沪科版数学七年级下册 10.2 平行线的判定 课件(共46张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 10.2 平行线的判定 课件(共46张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 855.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-17 17:13:39 | ||
图片预览










文档简介
(共46张PPT)
平行线的判定
二、重点和难点
1.了解两条直线的平行关系,掌握有关的符号表示。
2.学会用三角尺、量角器画平行线。
3.掌握平行线的性质。
重点:了解两条平行线的关系及有关性质。
难点:画平行线,理解平行线的含义。
一、学习目标
如图,电梯的扶手给我们什么印象?
电梯扶手所在直线会相交吗?
生活中好多事物给我们线的感觉,那么下列这些线给我们什么印象呢?
铁轨所在直线会相交吗?
那么铁轨给我们什么印象?还有什么地方给我们相同的印象呢?
双杠的两个握杠给我们什么印象?哪些地方也给我们这种印象?
生活中许多事物都给我们平行线的印象。
同一平面内,不相交的两条直线叫做平行线。
平行线的定义:
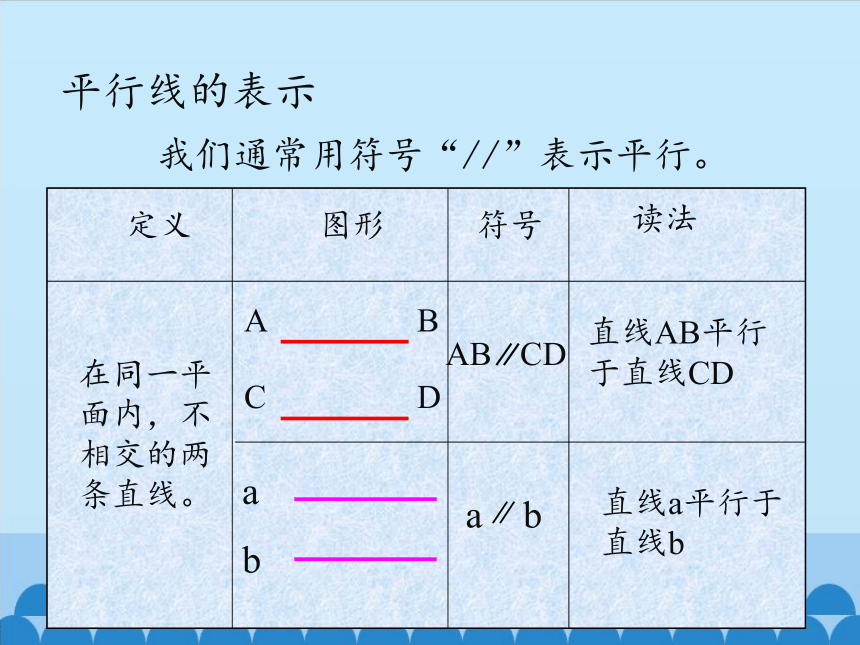
定义
在同一平面内,不相交的两条直线。
符号
图形
读法
A
B
C
D
AB
CD
a
b
直线AB平行于直线CD
直线a平行于直线b
a
b
我们通常用符号“//”表示平行。
平行线的表示
思考:在同一平面内,两条直线有几种位置关系?
相交
平行
垂直
1.判断下列说法是否正确,并说明理由。
①不相交的两条直线是平行线。 ( )
②在同一平面内,两条不相交的线段是平行线。( )
③过一点可以而且只可以画一条直线与已知直线平行。 ( )
2.用符号“∥”表示图中平行四边形的两组对边分别平行。
A
B
C
D
AB∥ CD,AD∥ BC。
课内练习
×
×
×
下列说法正确的是( )
A.在同一平面内,两条直线的位置关系有相交,垂直,平行三种。
B.在同一平面内,不垂直的两直线必平行。
C.在同一平面内,不平行的两直线必垂直。
D.在同一平面内,不相交的两直线一定不垂直。
D
巩固练习
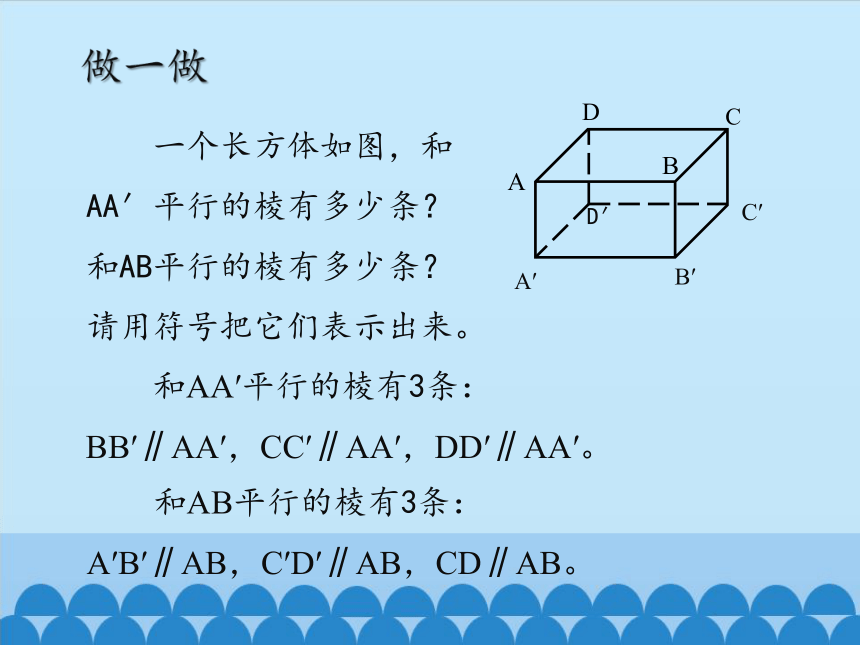
一个长方体如图,和AA′平行的棱有多少条?和AB平行的棱有多少条?请用符号把它们表示出来。
A′
B′
C′
D′
和AA′平行的棱有3条:
BB′∥AA′,CC′∥AA′,DD′∥AA′。
和AB平行的棱有3条:
A′B′∥AB,C′D′∥AB,CD∥AB。
做一做
1)观察如图所示的长方体后填空
①用符号表示下列两棱的位置关系:
A1B1____AB ,AA1____AB
A1D1____C1D1 , AD____BC
2)A1B1与BC所在的直线是两条不相交的直线,他们 平行线(填“是”或“不是”)。由此可知,在___________,两条不相交的直线才能叫平行线。
3)在同一平面内,两条不重合的直线位置关系只有_____种,即_____________。
A
B
C
D
A1
B1
C1
D1
课堂练习
∥
⊥
⊥
∥
不是
同一平面内
2
相交和平行
●
一、放
二、贴
三、推
四、画
过点P能否再画一条直线与AB平行?
例:已知直线AB和直线外一点P,过点P画一条直线和已知直线AB平行。
P
推平行线法
A
B
平面内经过直线外一点,有且只有一条直线与这条直线平行。
平行公理:
想一想
·
A
B
C
B
(垂直)
(唯一性)
问题:经过点C能画出几条直线与直线AB平行?
(1)你能在右图中的方格中画出平行线吗?
方法:
①利用方格纸中的直线画平行线。
②利用格点(长方形的对角线)画平行线。
(2)若改方格纸为白纸,你能利用以下哪些工具:①直尺 ②三角板 ③量角器能画已知直线AB的平行线?能画多少条?
试一试
推平行线法
可以画无数条
A
B
C
D
E
F
P
如图:AB∥EF, CD∥EF,
直线AB与CD相交吗?为什么?
c
b
a
//
//
//
//
(平行线的传递性)
如果a//c,
b//c;
那么a//b
推论:如果两条直线都平行于第三条直线,那么这两条直线也互相平行。
(如果两条直线都平行于第三条直线,那么这两条直线也互相平行)
∴ AB//CD
(已知)
F
D
B
A
C
E
∵ AB//EF,CD//EF
a
b
C
如果a⊥c, a⊥b
那么b//c
如果两条直线都垂直于第三条直线,那么这两条直线互相平行。
(2)观察直线 b、c是否平行?
(1)画一条直线 a,再画两条直线b、c分别与直线a垂直。
探究:
下列说法正确的是( )
A.在同一平面内,不相交的两条射线是平行线。
B.在同一平面内,不相交的两条线段是平行线。
C.在同一平面内,两条直线的位置关系不相交就平行。
D.不相交的两条直线是平行线。
C
做一做
1.互不重合的三条直线公共点的个数是_______________________
(0个,1个,2个或3个)
2.平面内的5条直线,如要使它们出现5个交点,怎样安排才能办到?画图说明。
做
一
做
小结
1.平行线的定义:
同一平面内,不相交的两条直线叫做平行线。
2.平行线的表示法
通常用符号“//”表示平行。
AB//CD或a//b
3.平行线的两条性质
平面内,经过直线外一点,有且只有一条直线与这条直线平行。
平行公理:
(唯一性)
推论:如果两条直线都平行于第三条直线,那么这两条直线也互相平行。
(平行线的传递性)
如果a//c,
b//c;
那么a//b
学习目标
1.经历探索直线平行判定的过程,掌握平行线的判定方法。
2.能运用平行线的判定方法进行简单的推理和计算。
自学提纲
自学课本内容
1.怎样过已知直线外一点画已知直线的平行线?
2.画图过程中,什么角始终保持相等。
3.直线l1,l2位置关系如何?
4.你能得到什么结论,怎样叙述这个结论?
5.如图,三根木条相交成∠1,∠2,固定木条b、c,转动木条a 。
当∠1,∠2满足什么条件时, b∥a。
温故思考
你会画已知直线的平行线的吗?
45°
45°
探索活动一
如图,三根木条相交成∠1,∠2,固定木条b、c,转动木条a 。
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
①直线a和b不平行
②直线a∥b
③直线a和b不平行
2
1
b
c
a
3
4
6
5
7
8
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单地说:同位角相等,两直线平行。
判定两直线平行方法1
因为∠ 1 =∠ 5 ,
所以a∥b
(同位角相等,两直线平行。 )
3.如果∠1 =∠C , ∠1=∠2。你能说明 AC∥BD吗?
学以致用
1.如图,如果∠1 =∠C,
那么直线 ∥ 。理由是 。
2.如图,如果∠2 =∠C,那么直线 ∥ 。理由是 。
CD
同位角相等,两直线平行
AC
同位角相等,两直线平行
2
1
AB
BD
4.如图,∠1 = ∠2 = 55°,∠3等于多少度?
直线AB、CD平行吗? 说明你的理由。
3
1
2
A
B
F
C
D
∵∠1 = ∠2 = 55°
∠3 = ∠2
∴∠3 =∠1= 55°
(对顶角相等)
∴ AB∥CD。
探究
如图,直线a、b被直线c所截,∠1= 40°,能添加一个条件使得直线a与直线b平行吗?
40°
1
a
b
c
2
3
4
5
5
思维拓展
在如图所示的图中,甲从A处沿东偏南55°方向行走,乙从B处沿东偏南35°方向行走。
(1)他们所行道路可能相交吗?
(2)当乙从B处沿什么方向行走,他们所行道路不相交?请说明其中的理由。
乙
甲
35°
55°
1
2
A
学习目标
1.掌握平行线的三种判定方法。并会运用所学方法来判断两条直线是否平行。
2.会根据判定方法进行简单的推理并学会用数学符号写出简单的推理过程。
3.体会数学中的转化思想。
自学提纲
阅读课本内容
1.平行线的判定方法有几种?
如何推理说明?
2.完成课本练习
两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
思考
a
b
c
1
2
3
解: ∵
∠ 1 = ∠ 3 (对顶角相等)
∴∠1= ∠2 (等量代换)
∴ a∥b (同位角相等,两直线平行)
探究1:如果 ∠2 = ∠3,能否推出 a//b呢?
∠2 = ∠3
(已知)
平行线的判定方法2
两条直线被第三条直线所截,如果
内错角相等,那么这两条直线平行。
内错角相等,两直线平行。
简单说成:
a
b
c
2
3
探究2:如果 ∠2+ ∠4= 180°,能得到 a//b吗?
解:∵ ∠1 + ∠4= 180°
∠2 + ∠4 = 180°
∴ ∠1 =∠2(同角的补角相等)
∴a∥b (同位角相等、两直线平行)
还有其他解法吗?
a
b
c
1
2
3
4
简单说成:
同旁内角互补,两直线平行
平行线的判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
a
b
c
1
2
3
4
例题1
① ∵ ∠1 =_____ (已知)
∴ AB∥CE
② ∵ ∠2 = (已知)
∴ CD∥BF
③ ∵ ∠1 +∠5 =180°(已知)
∴ _____∥_____
AB
CE
∠2
∠4
如图:
4
5
1
3
2
C
F
E
A
D
B
(内错角相等,两直线平行)
(同位角相等,两直线平行)
(同旁内角互补,两直线平行)
已知∠3=45 °,∠1与∠2互余,你能得到AB//CD ?
解∵∠1+∠2=90° ∠1=∠2
∴∠1=∠2=45°
∵ ∠3=45°
∴∠ 2=∠3
∴ AB∥CD(内错角相等,两直线平行)
1
2
3
A
B
C
D
例题2
(1)∵∠1=∠B(已知)
∴ ∥ 。
( )
(4)∵∠ = ∠ (已知)
∴AB∥CD( )
AD
(2)∵∠1=∠D(已知)
∴ ∥ ( )
(3)∵∠B+∠BAD=180°(已知)
∴ ∥ ( )
3
内错角相等,两直线平行
BC
练一练
同位角相等,两直线平行
BC
AB
DC
同旁内角互补,两直线平行
AD
内错角相等,两直线平行
5
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的判定示意图
判定
数量关系
位置关系
小结
课堂作业
必做:课本习题
选做:如图,BC、DE分别平分 ABD和 BDF,且 1= 2,请找出平行线,并说明理由。
A
B
D
F
C
E
2
1
3
4
课外作业
练习册同步。
预习平行线的性质。
谢 谢
平行线的判定
二、重点和难点
1.了解两条直线的平行关系,掌握有关的符号表示。
2.学会用三角尺、量角器画平行线。
3.掌握平行线的性质。
重点:了解两条平行线的关系及有关性质。
难点:画平行线,理解平行线的含义。
一、学习目标
如图,电梯的扶手给我们什么印象?
电梯扶手所在直线会相交吗?
生活中好多事物给我们线的感觉,那么下列这些线给我们什么印象呢?
铁轨所在直线会相交吗?
那么铁轨给我们什么印象?还有什么地方给我们相同的印象呢?
双杠的两个握杠给我们什么印象?哪些地方也给我们这种印象?
生活中许多事物都给我们平行线的印象。
同一平面内,不相交的两条直线叫做平行线。
平行线的定义:
定义
在同一平面内,不相交的两条直线。
符号
图形
读法
A
B
C
D
AB
CD
a
b
直线AB平行于直线CD
直线a平行于直线b
a
b
我们通常用符号“//”表示平行。
平行线的表示
思考:在同一平面内,两条直线有几种位置关系?
相交
平行
垂直
1.判断下列说法是否正确,并说明理由。
①不相交的两条直线是平行线。 ( )
②在同一平面内,两条不相交的线段是平行线。( )
③过一点可以而且只可以画一条直线与已知直线平行。 ( )
2.用符号“∥”表示图中平行四边形的两组对边分别平行。
A
B
C
D
AB∥ CD,AD∥ BC。
课内练习
×
×
×
下列说法正确的是( )
A.在同一平面内,两条直线的位置关系有相交,垂直,平行三种。
B.在同一平面内,不垂直的两直线必平行。
C.在同一平面内,不平行的两直线必垂直。
D.在同一平面内,不相交的两直线一定不垂直。
D
巩固练习
一个长方体如图,和AA′平行的棱有多少条?和AB平行的棱有多少条?请用符号把它们表示出来。
A′
B′
C′
D′
和AA′平行的棱有3条:
BB′∥AA′,CC′∥AA′,DD′∥AA′。
和AB平行的棱有3条:
A′B′∥AB,C′D′∥AB,CD∥AB。
做一做
1)观察如图所示的长方体后填空
①用符号表示下列两棱的位置关系:
A1B1____AB ,AA1____AB
A1D1____C1D1 , AD____BC
2)A1B1与BC所在的直线是两条不相交的直线,他们 平行线(填“是”或“不是”)。由此可知,在___________,两条不相交的直线才能叫平行线。
3)在同一平面内,两条不重合的直线位置关系只有_____种,即_____________。
A
B
C
D
A1
B1
C1
D1
课堂练习
∥
⊥
⊥
∥
不是
同一平面内
2
相交和平行
●
一、放
二、贴
三、推
四、画
过点P能否再画一条直线与AB平行?
例:已知直线AB和直线外一点P,过点P画一条直线和已知直线AB平行。
P
推平行线法
A
B
平面内经过直线外一点,有且只有一条直线与这条直线平行。
平行公理:
想一想
·
A
B
C
B
(垂直)
(唯一性)
问题:经过点C能画出几条直线与直线AB平行?
(1)你能在右图中的方格中画出平行线吗?
方法:
①利用方格纸中的直线画平行线。
②利用格点(长方形的对角线)画平行线。
(2)若改方格纸为白纸,你能利用以下哪些工具:①直尺 ②三角板 ③量角器能画已知直线AB的平行线?能画多少条?
试一试
推平行线法
可以画无数条
A
B
C
D
E
F
P
如图:AB∥EF, CD∥EF,
直线AB与CD相交吗?为什么?
c
b
a
//
//
//
//
(平行线的传递性)
如果a//c,
b//c;
那么a//b
推论:如果两条直线都平行于第三条直线,那么这两条直线也互相平行。
(如果两条直线都平行于第三条直线,那么这两条直线也互相平行)
∴ AB//CD
(已知)
F
D
B
A
C
E
∵ AB//EF,CD//EF
a
b
C
如果a⊥c, a⊥b
那么b//c
如果两条直线都垂直于第三条直线,那么这两条直线互相平行。
(2)观察直线 b、c是否平行?
(1)画一条直线 a,再画两条直线b、c分别与直线a垂直。
探究:
下列说法正确的是( )
A.在同一平面内,不相交的两条射线是平行线。
B.在同一平面内,不相交的两条线段是平行线。
C.在同一平面内,两条直线的位置关系不相交就平行。
D.不相交的两条直线是平行线。
C
做一做
1.互不重合的三条直线公共点的个数是_______________________
(0个,1个,2个或3个)
2.平面内的5条直线,如要使它们出现5个交点,怎样安排才能办到?画图说明。
做
一
做
小结
1.平行线的定义:
同一平面内,不相交的两条直线叫做平行线。
2.平行线的表示法
通常用符号“//”表示平行。
AB//CD或a//b
3.平行线的两条性质
平面内,经过直线外一点,有且只有一条直线与这条直线平行。
平行公理:
(唯一性)
推论:如果两条直线都平行于第三条直线,那么这两条直线也互相平行。
(平行线的传递性)
如果a//c,
b//c;
那么a//b
学习目标
1.经历探索直线平行判定的过程,掌握平行线的判定方法。
2.能运用平行线的判定方法进行简单的推理和计算。
自学提纲
自学课本内容
1.怎样过已知直线外一点画已知直线的平行线?
2.画图过程中,什么角始终保持相等。
3.直线l1,l2位置关系如何?
4.你能得到什么结论,怎样叙述这个结论?
5.如图,三根木条相交成∠1,∠2,固定木条b、c,转动木条a 。
当∠1,∠2满足什么条件时, b∥a。
温故思考
你会画已知直线的平行线的吗?
45°
45°
探索活动一
如图,三根木条相交成∠1,∠2,固定木条b、c,转动木条a 。
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
①直线a和b不平行
②直线a∥b
③直线a和b不平行
2
1
b
c
a
3
4
6
5
7
8
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单地说:同位角相等,两直线平行。
判定两直线平行方法1
因为∠ 1 =∠ 5 ,
所以a∥b
(同位角相等,两直线平行。 )
3.如果∠1 =∠C , ∠1=∠2。你能说明 AC∥BD吗?
学以致用
1.如图,如果∠1 =∠C,
那么直线 ∥ 。理由是 。
2.如图,如果∠2 =∠C,那么直线 ∥ 。理由是 。
CD
同位角相等,两直线平行
AC
同位角相等,两直线平行
2
1
AB
BD
4.如图,∠1 = ∠2 = 55°,∠3等于多少度?
直线AB、CD平行吗? 说明你的理由。
3
1
2
A
B
F
C
D
∵∠1 = ∠2 = 55°
∠3 = ∠2
∴∠3 =∠1= 55°
(对顶角相等)
∴ AB∥CD。
探究
如图,直线a、b被直线c所截,∠1= 40°,能添加一个条件使得直线a与直线b平行吗?
40°
1
a
b
c
2
3
4
5
5
思维拓展
在如图所示的图中,甲从A处沿东偏南55°方向行走,乙从B处沿东偏南35°方向行走。
(1)他们所行道路可能相交吗?
(2)当乙从B处沿什么方向行走,他们所行道路不相交?请说明其中的理由。
乙
甲
35°
55°
1
2
A
学习目标
1.掌握平行线的三种判定方法。并会运用所学方法来判断两条直线是否平行。
2.会根据判定方法进行简单的推理并学会用数学符号写出简单的推理过程。
3.体会数学中的转化思想。
自学提纲
阅读课本内容
1.平行线的判定方法有几种?
如何推理说明?
2.完成课本练习
两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
思考
a
b
c
1
2
3
解: ∵
∠ 1 = ∠ 3 (对顶角相等)
∴∠1= ∠2 (等量代换)
∴ a∥b (同位角相等,两直线平行)
探究1:如果 ∠2 = ∠3,能否推出 a//b呢?
∠2 = ∠3
(已知)
平行线的判定方法2
两条直线被第三条直线所截,如果
内错角相等,那么这两条直线平行。
内错角相等,两直线平行。
简单说成:
a
b
c
2
3
探究2:如果 ∠2+ ∠4= 180°,能得到 a//b吗?
解:∵ ∠1 + ∠4= 180°
∠2 + ∠4 = 180°
∴ ∠1 =∠2(同角的补角相等)
∴a∥b (同位角相等、两直线平行)
还有其他解法吗?
a
b
c
1
2
3
4
简单说成:
同旁内角互补,两直线平行
平行线的判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
a
b
c
1
2
3
4
例题1
① ∵ ∠1 =_____ (已知)
∴ AB∥CE
② ∵ ∠2 = (已知)
∴ CD∥BF
③ ∵ ∠1 +∠5 =180°(已知)
∴ _____∥_____
AB
CE
∠2
∠4
如图:
4
5
1
3
2
C
F
E
A
D
B
(内错角相等,两直线平行)
(同位角相等,两直线平行)
(同旁内角互补,两直线平行)
已知∠3=45 °,∠1与∠2互余,你能得到AB//CD ?
解∵∠1+∠2=90° ∠1=∠2
∴∠1=∠2=45°
∵ ∠3=45°
∴∠ 2=∠3
∴ AB∥CD(内错角相等,两直线平行)
1
2
3
A
B
C
D
例题2
(1)∵∠1=∠B(已知)
∴ ∥ 。
( )
(4)∵∠ = ∠ (已知)
∴AB∥CD( )
AD
(2)∵∠1=∠D(已知)
∴ ∥ ( )
(3)∵∠B+∠BAD=180°(已知)
∴ ∥ ( )
3
内错角相等,两直线平行
BC
练一练
同位角相等,两直线平行
BC
AB
DC
同旁内角互补,两直线平行
AD
内错角相等,两直线平行
5
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的判定示意图
判定
数量关系
位置关系
小结
课堂作业
必做:课本习题
选做:如图,BC、DE分别平分 ABD和 BDF,且 1= 2,请找出平行线,并说明理由。
A
B
D
F
C
E
2
1
3
4
课外作业
练习册同步。
预习平行线的性质。
谢 谢
