沪科版数学七年级下册 第7章 一元一次不等式与不等式组 复习 课件(共22张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 第7章 一元一次不等式与不等式组 复习 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 389.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-17 18:33:08 | ||
图片预览







文档简介
(共22张PPT)
第7章 一元一次不等式与不等式组 复习课件
学习目标:
(1)进一步理解不等式及其基本性质;
(2)熟练掌握解一元一次不等式和一元一次不等式组,并能运用一元一次不等式和一元一次不等式组解决具体的实际问题。
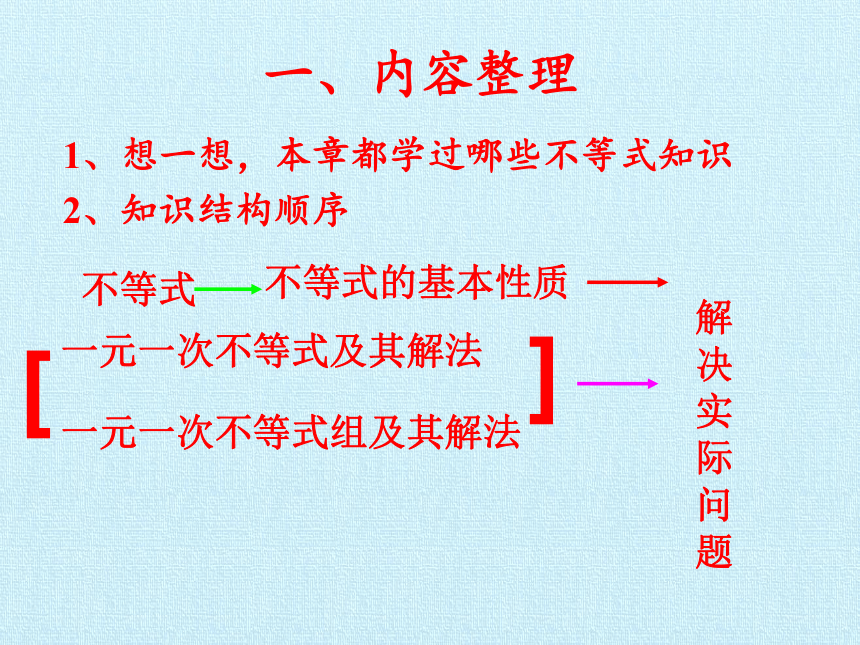
一、内容整理
1、想一想,本章都学过哪些不等式知识
2、知识结构顺序
不等式的基本性质
一元一次不等式组及其解法
解
决
实
际
问
题
[
一元一次不等式及其解法
]
不等式
二、
1、不等式的基本性质是什么?它与等式的基本性质有哪些相同点与不同点。
例1、用“大于”或“小于”号填空。
(1)如果a-1(2)如果3a>3b,那么a b
(3)如果-2a<-2b,那么a b
(4)如果2a+1<2b+1,那么a b
(5)巩固练习:已知m>n,若m<0则㎡ mn;若m>0,则㎡ mn
<
>
<
>
>
<
2、一元一次不等式的解法与一元一次方程的解法有什么联系?它们不同的地方是什么?
例2、解不等式,并把解集在数轴上表示出来
(1)2(x-3)-3(x-2)>0
(2) x+5 3x+1
2
3
_
≥0
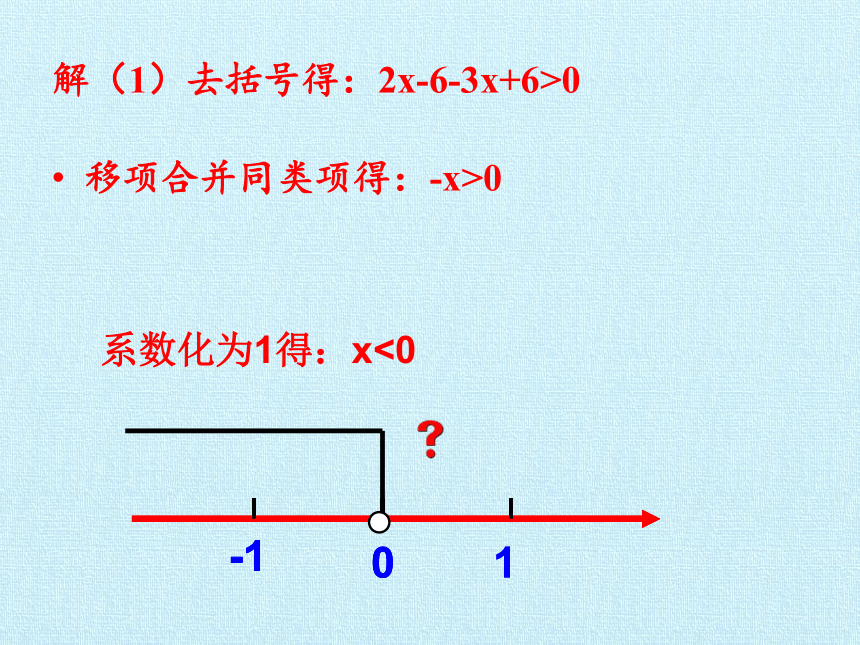
解(1)去括号得:2x-6-3x+6>0
移项合并同类项得:-x>0
系数化为1得:x<0
-1
0
1
-1
0
-1
1
0
-1
解:
(2)去分母得:2(x+5)-3(3x+1)≥0
去括号得:2x+10-9x-3≥0
移项合并同类项得:-7x≥-7
系数化为1得:x≤1
-1
0
1
3、一元一次不等式组的解集有几种情况?解一元一次不等式组与解一元一次不等式有什么联系?
例1 解不等式组:
2x-1> -x
<3
①②
解:解不等式①,得
解不等式②,得
x< 6
在同一条数轴上表示不等式①②的解集,
如下图
0
1
2
3
4
5
6
7
-1
。
。
因此,不等式组的解集为
例 题 解 析
例1 求下列不等式组的解集:
解:原不等式组的解集为x>7;
写解集规律
0
7
6
5
4
2
1
3
8
9
解:原不等式组的解集为x>-2;
-6
1
0
-1
-2
-4
-5
-3
2
3
同大取大
例1 求下列不等式组的解集:
解:原不等式组的解集为x≤3;
解:原不等式组的解集为x≤-5;
写解集规律
0
7
6
5
4
2
1
3
8
9
-7
0
-1
-2
-3
-5
-6
-4
1
2
同小取小
例1 求下列不等式组的解集:
解:原不等式组的解集为3解:原不等式组的解集为-5写解集规律
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
大小小大中间找
例1 求下列不等式组的解集:
解:原不等式组无解;
写解集规律
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
解:原不等式组无解;
大大小小无处找
{
练习
+1<2(x-1)
x
3
x+2
5
>
x
2
(1)
(2)
{
2x+7>3x-1
X-2
5
≥
0
专题
求不等式(组)的特殊解
(1)
y+1
3
y-1
2
≥
y-1
6
的正整数解
4、对于实际问题中存在的数量不等关系,我们可以用不等式相关知识去解决。
1.跳高组的趣事
在运动会上,跳高组裁判员的点心是一个面包加一瓶饮料,一个面包3元、一瓶饮料2元,学校为跳高组所付的金额超过27元,但不到33元。设跳高组裁判员有x人,你能列出几个不等式?
你能求出跳高组裁判员人数?
解
①
②
由①得
由②得
答:跳高组裁判员有6人。
解
①
解
②
①
解
2.用若干辆载重量为7吨的汽车运一批货物,若每辆汽车只装4吨,则剩下10吨货物,若每辆汽车装满7吨,则最后一辆汽车不满也不空。请问:有多少辆汽车?
分析:设有x辆汽车,则有4x+10吨货物,(x-1)辆汽车装满了7吨,最后一辆装4x+10-7(x-1)吨,根据不满也不空,可列出不等式:
4x+10-7(x-1)>0
4x+10-7(x-1)<7
答案:有4辆汽车或者5辆汽车。
3.某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg。
(1)设生产X件A种产品,写出X应满足的不等式组。
(2)有哪几种符合的生产方案?
(3)若生产一件A产品可获利700元,生产一件B产品可获利1200元,那么采用哪种生产方案可使生产A、B两种产品的总获利最大?最大利润是多少?
思路分析:
(1)本题的不等关系是:
生产A种产品所需的甲种原料≤360
生产B种产品所需的乙种原料≤290
根据上述关系可列不等式组:
9x+4(50-X)≤360
3x+10(50-x)≤290
解得:30≤X≤32
(2)可有三种生产方案:A种30件,B种20件或A种31件,B种19件或A种32件,B种18件。
谢 谢
第7章 一元一次不等式与不等式组 复习课件
学习目标:
(1)进一步理解不等式及其基本性质;
(2)熟练掌握解一元一次不等式和一元一次不等式组,并能运用一元一次不等式和一元一次不等式组解决具体的实际问题。
一、内容整理
1、想一想,本章都学过哪些不等式知识
2、知识结构顺序
不等式的基本性质
一元一次不等式组及其解法
解
决
实
际
问
题
[
一元一次不等式及其解法
]
不等式
二、
1、不等式的基本性质是什么?它与等式的基本性质有哪些相同点与不同点。
例1、用“大于”或“小于”号填空。
(1)如果a-1
(3)如果-2a<-2b,那么a b
(4)如果2a+1<2b+1,那么a b
(5)巩固练习:已知m>n,若m<0则㎡ mn;若m>0,则㎡ mn
<
>
<
>
>
<
2、一元一次不等式的解法与一元一次方程的解法有什么联系?它们不同的地方是什么?
例2、解不等式,并把解集在数轴上表示出来
(1)2(x-3)-3(x-2)>0
(2) x+5 3x+1
2
3
_
≥0
解(1)去括号得:2x-6-3x+6>0
移项合并同类项得:-x>0
系数化为1得:x<0
-1
0
1
-1
0
-1
1
0
-1
解:
(2)去分母得:2(x+5)-3(3x+1)≥0
去括号得:2x+10-9x-3≥0
移项合并同类项得:-7x≥-7
系数化为1得:x≤1
-1
0
1
3、一元一次不等式组的解集有几种情况?解一元一次不等式组与解一元一次不等式有什么联系?
例1 解不等式组:
2x-1> -x
<3
①②
解:解不等式①,得
解不等式②,得
x< 6
在同一条数轴上表示不等式①②的解集,
如下图
0
1
2
3
4
5
6
7
-1
。
。
因此,不等式组的解集为
例 题 解 析
例1 求下列不等式组的解集:
解:原不等式组的解集为x>7;
写解集规律
0
7
6
5
4
2
1
3
8
9
解:原不等式组的解集为x>-2;
-6
1
0
-1
-2
-4
-5
-3
2
3
同大取大
例1 求下列不等式组的解集:
解:原不等式组的解集为x≤3;
解:原不等式组的解集为x≤-5;
写解集规律
0
7
6
5
4
2
1
3
8
9
-7
0
-1
-2
-3
-5
-6
-4
1
2
同小取小
例1 求下列不等式组的解集:
解:原不等式组的解集为3
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
大小小大中间找
例1 求下列不等式组的解集:
解:原不等式组无解;
写解集规律
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
解:原不等式组无解;
大大小小无处找
{
练习
+1<2(x-1)
x
3
x+2
5
>
x
2
(1)
(2)
{
2x+7>3x-1
X-2
5
≥
0
专题
求不等式(组)的特殊解
(1)
y+1
3
y-1
2
≥
y-1
6
的正整数解
4、对于实际问题中存在的数量不等关系,我们可以用不等式相关知识去解决。
1.跳高组的趣事
在运动会上,跳高组裁判员的点心是一个面包加一瓶饮料,一个面包3元、一瓶饮料2元,学校为跳高组所付的金额超过27元,但不到33元。设跳高组裁判员有x人,你能列出几个不等式?
你能求出跳高组裁判员人数?
解
①
②
由①得
由②得
答:跳高组裁判员有6人。
解
①
解
②
①
解
2.用若干辆载重量为7吨的汽车运一批货物,若每辆汽车只装4吨,则剩下10吨货物,若每辆汽车装满7吨,则最后一辆汽车不满也不空。请问:有多少辆汽车?
分析:设有x辆汽车,则有4x+10吨货物,(x-1)辆汽车装满了7吨,最后一辆装4x+10-7(x-1)吨,根据不满也不空,可列出不等式:
4x+10-7(x-1)>0
4x+10-7(x-1)<7
答案:
3.某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg。
(1)设生产X件A种产品,写出X应满足的不等式组。
(2)有哪几种符合的生产方案?
(3)若生产一件A产品可获利700元,生产一件B产品可获利1200元,那么采用哪种生产方案可使生产A、B两种产品的总获利最大?最大利润是多少?
思路分析:
(1)本题的不等关系是:
生产A种产品所需的甲种原料≤360
生产B种产品所需的乙种原料≤290
根据上述关系可列不等式组:
9x+4(50-X)≤360
3x+10(50-x)≤290
解得:30≤X≤32
(2)可有三种生产方案:A种30件,B种20件或A种31件,B种19件或A种32件,B种18件。
谢 谢
