第四单元 因式分解单元检测卷A(含解析)
文档属性
| 名称 | 第四单元 因式分解单元检测卷A(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-16 21:48:03 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大八年级数学下册第四单元因式分解检测卷(A)
一.选择题(共10小题,每小题3分,满分30分)
1.(3分)下列等式从左到右的变形,属于因式分解的是
A. B.
C. D.
2.(3分)下列四个多项式:①;②;③;④,其中能用平方差公式分解因式的有
A.4个 B.3个 C.2个 D.1个
3.(3分)利用因式分解简便计算正确的是
A.
B.
C.
D.
4.(3分)若,则值为
A. B.或13 C.11或 D.11
5.(3分)已知,,,则多项式的值为
A.1 B.2 C.3 D.4
6.(3分)若,则的值为
A.27 B.11 C.3 D.0
7.(3分)已知,,为的三边长,且满足,则的形状是
A.等边三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形
8.(3分)若为任意整数,且能被整除,则不可能是
A.100 B.99 C.98 D.97
9.(3分)在探索因式分解的公式时,可以借助几何图形来解释某些公式.如图,从左图到右图的变化过程中,解释的因式分解公式是
A. B.
C. D.
10.(3分)小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:,,2,,,,分别对应下列六个字:海、爱、我、美、游、北,现将因式分解,结果呈现的密码信息可能是
A.我爱游 B.北海游 C.我爱北海 D.美我北海
二.填空题(共5小题,每小题3分,满分15分)
11.(3分)因式分解: .
12.(3分)的三边,,为互不相同的整数,且,则的周长为 .
13.(3分)将几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式例如,由图(1)可得等式:.将图(2)所示的卡片若干张进行拼图,可以将二次三项式分解因式为 .
14.(3分)若,则的值为 .
15.(3分)在日常生活中如取款、上网等都需要密码,有一种用“因式分解法”产生的密码,方便记忆,原理是对于多项,因式分解的结果是,若取,时,则各个因式的值是:,,,于是就可以把“180162”作为一个六位数的密码,对于多项式,取,时,用上述方法产生的密码是 (写出一个即可).
三.解答题(共7小题,满分55分)
16.(8分)分解因式:
(1); (2);
(3); (4).
17.(7分)给出三个多项式:,,.请选择你最喜欢的两个多项式进行加法运算,并把结果因式分解.
18.(8分)对于任意自然数,代数式的值都能被4整除吗?请说明理由.
19.(8分)阅读某同学对多项式进行因式分解的过程,并解决问题:
解:设,
原式(第一步)
(第二步)
(第三步)
(第四步)
(1)该同学第二步到第三步的变形运用了 (填序号);
.提公因式法 .平方差公式 .两数和的平方公式 .两数差的平方公式
(2)该同学在第三步用所设的代数式进行了代换,得到第四步的结果,这个结果能否进一步因式分解? (填“能”或“不能” .如果能,直接写出最后结果 .
(3)请你模仿以上方法尝试对多项式进行因式分行解.
20.(8分)阅读材料:若,求、的值.
解:,
,,,,.
根据你的观察,探究下面的问题:
(1) 已知,求的值;
(2)已知,,求的值.
21.(8分)仔细阅读下面例题,解答问题:
例题:已知二次三项式有一个因式是,求另一个因式以及的值.
解:设另一个因式为,得
则
解得:,
另一个因式为,的值为
问题:仿照以上方法解答下面问题:
已知二次三项式有一个因式是,求另一个因式以及的值.
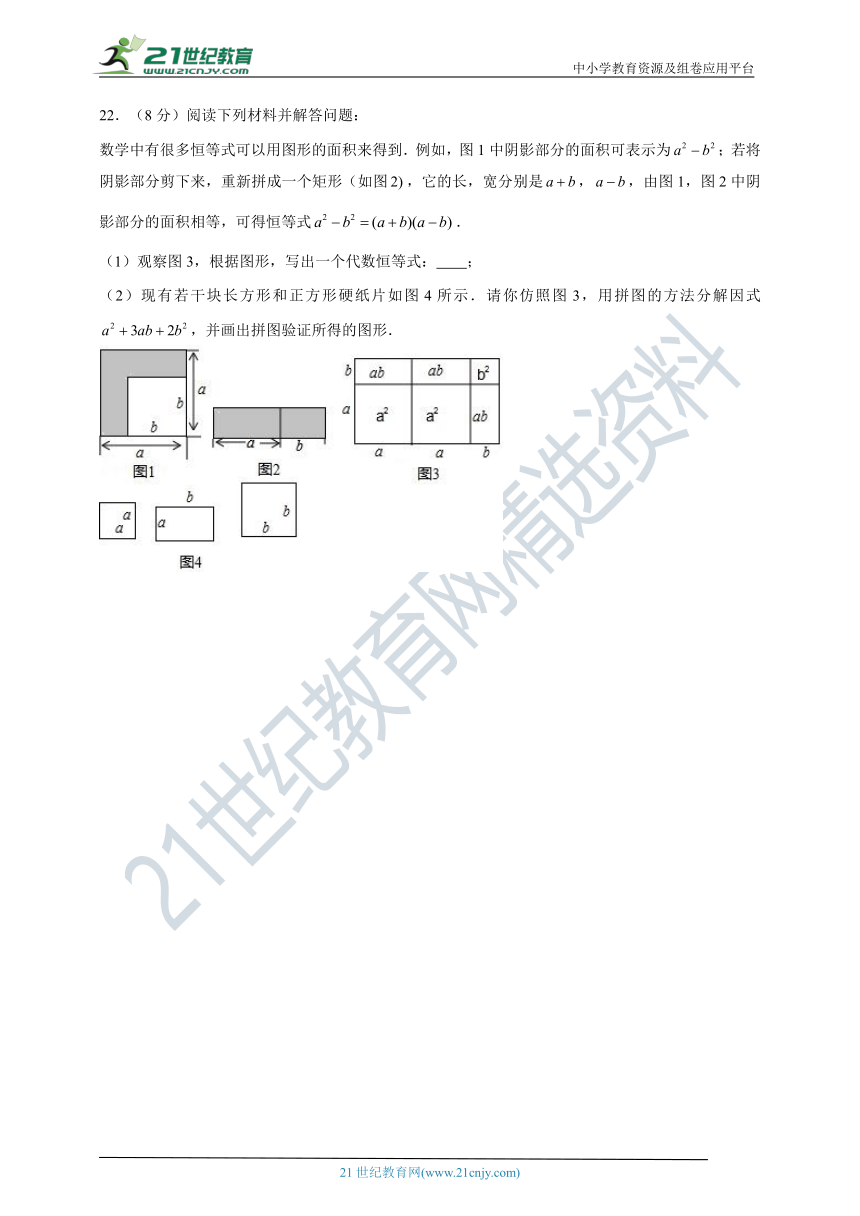
22.(8分)阅读下列材料并解答问题:
数学中有很多恒等式可以用图形的面积来得到.例如,图1中阴影部分的面积可表示为;若将阴影部分剪下来,重新拼成一个矩形(如图,它的长,宽分别是,,由图1,图2中阴影部分的面积相等,可得恒等式.
(1)观察图3,根据图形,写出一个代数恒等式: ;
(2)现有若干块长方形和正方形硬纸片如图4所示.请你仿照图3,用拼图的方法分解因式,并画出拼图验证所得的图形.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)下列等式从左到右的变形,属于因式分解的是
A. B.
C. D.
【解答】解:、左边不符合完全平方公式,因式分解错误,故此选项不符合题意;
、从左到右是整式的乘法,不是因式分解,故此选项不符合题意;
、右边是几个整式的积的形式,故此选项符合题意;
、右边不是把多项式化成整式的积的形式,故此选项不符合题意.
故选:.
2.(3分)下列四个多项式:①;②;③;④,其中能用平方差公式分解因式的有
A.4个 B.3个 C.2个 D.1个
【解答】解:①,③,能用平方差公式分解因式,
②;④,不能用平方差公式分解因式,
即能用平方差公式分解因式的有2个,
故选:.
3.(3分)利用因式分解简便计算正确的是
A.
B.
C.
D.
【解答】解:
.
故选:.
4.(3分)若,则值为
A. B.或13 C.11或 D.11
【解答】解:已知等式整理得:,
可得,
解得:,
故选:.
5.(3分)已知,,,则多项式的值为
A.1 B.2 C.3 D.4
【解答】解:由题意可知,,,
所求式,
,
,
,
.
故选:.
6.(3分)若,则的值为
A.27 B.11 C.3 D.0
【解答】解:,
,
故选:.
7.(3分)已知,,为的三边长,且满足,则的形状是
A.等边三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形
【解答】解:由得,,
,
是等腰三角形.
故选:.
8.(3分)若为任意整数,且能被整除,则不可能是
A.100 B.99 C.98 D.97
【解答】解:
能被整除,
可能是98、99、100,
不可能是97.
故选:.
9.(3分)在探索因式分解的公式时,可以借助几何图形来解释某些公式.如图,从左图到右图的变化过程中,解释的因式分解公式是
A. B.
C. D.
【解答】解:如图,从左图到右图的变化过程中,解释的因式分解公式是:,
故选:.
10.(3分)小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:,,2,,,,分别对应下列六个字:海、爱、我、美、游、北,现将因式分解,结果呈现的密码信息可能是
A.我爱游 B.北海游 C.我爱北海 D.美我北海
【解答】解:
,
,,2,,,,分别对应下列六个字:海、爱、我、美、游、北,
当出现时,对应的是“我爱美”,故、错误,
当出现时,对应的是“我爱北海”,故正确,错误,
故选:.
二.填空题(共5小题,满分15分,每小题3分)
11.(3分)因式分解: .
【解答】解:
.
故答案为:.
12.(3分)的三边,,为互不相同的整数,且,则的周长为 12 .
【解答】解:
,,为互不相同的整数,且是的三边
,,也是互不相同的正整数,且都大于1.
故可分为以下6种情况:
(1),即的三边长分别为2,3,9;由三角形的三边关系可知不合题意,舍去.
(2),即的三边长分别为2,1,19;由三角形的三边关系可知不合题意,舍去.
(3),即的三边长分别为2,7,4;由三角形的三边关系可知不合题意,舍去.
(4),即的三边长分别为5,3,4;即,.
(5),即的三边长分别为5,1,9;由三角形的三边关系可知不合题意,舍去.
(6),即的三边长分别为11,1,4;由三角形的三边关系可知不合题意,舍去.
(7),即的三边长分别为2,4,15;由三角形的三边关系可知不合题意,舍去.
综上可知,的周长为12.
故答案为12.
13.(3分)将几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式例如,由图(1)可得等式:.将图(2)所示的卡片若干张进行拼图,可以将二次三项式分解因式为 .
【解答】解:,
画图如下:
故答案是:.
14.(3分)若,则的值为 3 .
【解答】解:,
,
解得:,,
则,
故答案为:3.
15.(3分)在日常生活中如取款、上网等都需要密码,有一种用“因式分解法”产生的密码,方便记忆,原理是对于多项,因式分解的结果是,若取,时,则各个因式的值是:,,,于是就可以把“180162”作为一个六位数的密码,对于多项式,取,时,用上述方法产生的密码是 104020(答案不唯一) (写出一个即可).
【解答】解:,
当,时,密码可以是104020或102040等等都可以,答案不唯一.
三.解答题(共7小题,满分55分)
16.(8分)分解因式:
(1);
(2);
(3);
(4).
【解答】解:(1)原式;
(2)原式
;
(3)原式
;
(4)原式
.
17.(7分)给出三个多项式:,,.请选择你最喜欢的两个多项式进行加法运算,并把结果因式分解.
【解答】解:情况一:.
情况二:.
情况三:.
18.(8分)对于任意自然数,代数式的值都能被4整除吗?请说明理由.
【解答】解:能被4整除.
理由:原式,
为自然数,
与两数必有一数为偶数,
是4的倍数,
对于任意自然数,代数式的值都能被4整除.
19.(8分)阅读某同学对多项式进行因式分解的过程,并解决问题:
解:设,
原式(第一步)
(第二步)
(第三步)
(第四步)
(1)该同学第二步到第三步的变形运用了 (填序号);
.提公因式法 .平方差公式
.两数和的平方公式 .两数差的平方公式
(2)该同学在第三步用所设的代数式进行了代换,得到第四步的结果,这个结果能否进一步因式分解? (填“能”或“不能” .如果能,直接写出最后结果 .
(3)请你模仿以上方法尝试对多项式进行因式分行解.
【解答】解:(1)该同学第二步到第三步的变形运用了两数和的平方公式,
故选;
(2)该同学在第三步用所设的代数式进行了代换,得到第四步的结果,这个结果能进一步因式分解,
最后结果,
故答案为 能,;
(3)设
.
20.(8分)阅读材料:若,求、的值.
解:,
,,,,.
根据你的观察,探究下面的问题:
(1)已知,求的值;
(2)已知,,求的值.
【解答】解:(1),
,
,
,,
解得,,,
;
(2),
,
将代入,得
,
,
,
,,
解得,,,
,
.
21.(8分)仔细阅读下面例题,解答问题:
例题:已知二次三项式有一个因式是,求另一个因式以及的值.
解:设另一个因式为,得
则
解得:,
另一个因式为,的值为
问题:仿照以上方法解答下面问题:
已知二次三项式有一个因式是,求另一个因式以及的值.
【解答】解:设另一个因式为,得:
,
则,
,
解得:,,
故另一个因式为,的值为20.
22.(8分)阅读下列材料并解答问题:
数学中有很多恒等式可以用图形的面积来得到.例如,图1中阴影部分的面积可表示为;若将阴影部分剪下来,重新拼成一个矩形(如图,它的长,宽分别是,,由图1,图2中阴影部分的面积相等,可得恒等式.
(1)观察图3,根据图形,写出一个代数恒等式: ;
(2)现有若干块长方形和正方形硬纸片如图4所示.请你仿照图3,用拼图的方法分解因式,并画出拼图验证所得的图形.
【解答】解,(1)由图3知,等式为.
(2)
如图:
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
北师大八年级数学下册第四单元因式分解检测卷(A)
一.选择题(共10小题,每小题3分,满分30分)
1.(3分)下列等式从左到右的变形,属于因式分解的是
A. B.
C. D.
2.(3分)下列四个多项式:①;②;③;④,其中能用平方差公式分解因式的有
A.4个 B.3个 C.2个 D.1个
3.(3分)利用因式分解简便计算正确的是
A.
B.
C.
D.
4.(3分)若,则值为
A. B.或13 C.11或 D.11
5.(3分)已知,,,则多项式的值为
A.1 B.2 C.3 D.4
6.(3分)若,则的值为
A.27 B.11 C.3 D.0
7.(3分)已知,,为的三边长,且满足,则的形状是
A.等边三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形
8.(3分)若为任意整数,且能被整除,则不可能是
A.100 B.99 C.98 D.97
9.(3分)在探索因式分解的公式时,可以借助几何图形来解释某些公式.如图,从左图到右图的变化过程中,解释的因式分解公式是
A. B.
C. D.
10.(3分)小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:,,2,,,,分别对应下列六个字:海、爱、我、美、游、北,现将因式分解,结果呈现的密码信息可能是
A.我爱游 B.北海游 C.我爱北海 D.美我北海
二.填空题(共5小题,每小题3分,满分15分)
11.(3分)因式分解: .
12.(3分)的三边,,为互不相同的整数,且,则的周长为 .
13.(3分)将几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式例如,由图(1)可得等式:.将图(2)所示的卡片若干张进行拼图,可以将二次三项式分解因式为 .
14.(3分)若,则的值为 .
15.(3分)在日常生活中如取款、上网等都需要密码,有一种用“因式分解法”产生的密码,方便记忆,原理是对于多项,因式分解的结果是,若取,时,则各个因式的值是:,,,于是就可以把“180162”作为一个六位数的密码,对于多项式,取,时,用上述方法产生的密码是 (写出一个即可).
三.解答题(共7小题,满分55分)
16.(8分)分解因式:
(1); (2);
(3); (4).
17.(7分)给出三个多项式:,,.请选择你最喜欢的两个多项式进行加法运算,并把结果因式分解.
18.(8分)对于任意自然数,代数式的值都能被4整除吗?请说明理由.
19.(8分)阅读某同学对多项式进行因式分解的过程,并解决问题:
解:设,
原式(第一步)
(第二步)
(第三步)
(第四步)
(1)该同学第二步到第三步的变形运用了 (填序号);
.提公因式法 .平方差公式 .两数和的平方公式 .两数差的平方公式
(2)该同学在第三步用所设的代数式进行了代换,得到第四步的结果,这个结果能否进一步因式分解? (填“能”或“不能” .如果能,直接写出最后结果 .
(3)请你模仿以上方法尝试对多项式进行因式分行解.
20.(8分)阅读材料:若,求、的值.
解:,
,,,,.
根据你的观察,探究下面的问题:
(1) 已知,求的值;
(2)已知,,求的值.
21.(8分)仔细阅读下面例题,解答问题:
例题:已知二次三项式有一个因式是,求另一个因式以及的值.
解:设另一个因式为,得
则
解得:,
另一个因式为,的值为
问题:仿照以上方法解答下面问题:
已知二次三项式有一个因式是,求另一个因式以及的值.
22.(8分)阅读下列材料并解答问题:
数学中有很多恒等式可以用图形的面积来得到.例如,图1中阴影部分的面积可表示为;若将阴影部分剪下来,重新拼成一个矩形(如图,它的长,宽分别是,,由图1,图2中阴影部分的面积相等,可得恒等式.
(1)观察图3,根据图形,写出一个代数恒等式: ;
(2)现有若干块长方形和正方形硬纸片如图4所示.请你仿照图3,用拼图的方法分解因式,并画出拼图验证所得的图形.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)下列等式从左到右的变形,属于因式分解的是
A. B.
C. D.
【解答】解:、左边不符合完全平方公式,因式分解错误,故此选项不符合题意;
、从左到右是整式的乘法,不是因式分解,故此选项不符合题意;
、右边是几个整式的积的形式,故此选项符合题意;
、右边不是把多项式化成整式的积的形式,故此选项不符合题意.
故选:.
2.(3分)下列四个多项式:①;②;③;④,其中能用平方差公式分解因式的有
A.4个 B.3个 C.2个 D.1个
【解答】解:①,③,能用平方差公式分解因式,
②;④,不能用平方差公式分解因式,
即能用平方差公式分解因式的有2个,
故选:.
3.(3分)利用因式分解简便计算正确的是
A.
B.
C.
D.
【解答】解:
.
故选:.
4.(3分)若,则值为
A. B.或13 C.11或 D.11
【解答】解:已知等式整理得:,
可得,
解得:,
故选:.
5.(3分)已知,,,则多项式的值为
A.1 B.2 C.3 D.4
【解答】解:由题意可知,,,
所求式,
,
,
,
.
故选:.
6.(3分)若,则的值为
A.27 B.11 C.3 D.0
【解答】解:,
,
故选:.
7.(3分)已知,,为的三边长,且满足,则的形状是
A.等边三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形
【解答】解:由得,,
,
是等腰三角形.
故选:.
8.(3分)若为任意整数,且能被整除,则不可能是
A.100 B.99 C.98 D.97
【解答】解:
能被整除,
可能是98、99、100,
不可能是97.
故选:.
9.(3分)在探索因式分解的公式时,可以借助几何图形来解释某些公式.如图,从左图到右图的变化过程中,解释的因式分解公式是
A. B.
C. D.
【解答】解:如图,从左图到右图的变化过程中,解释的因式分解公式是:,
故选:.
10.(3分)小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:,,2,,,,分别对应下列六个字:海、爱、我、美、游、北,现将因式分解,结果呈现的密码信息可能是
A.我爱游 B.北海游 C.我爱北海 D.美我北海
【解答】解:
,
,,2,,,,分别对应下列六个字:海、爱、我、美、游、北,
当出现时,对应的是“我爱美”,故、错误,
当出现时,对应的是“我爱北海”,故正确,错误,
故选:.
二.填空题(共5小题,满分15分,每小题3分)
11.(3分)因式分解: .
【解答】解:
.
故答案为:.
12.(3分)的三边,,为互不相同的整数,且,则的周长为 12 .
【解答】解:
,,为互不相同的整数,且是的三边
,,也是互不相同的正整数,且都大于1.
故可分为以下6种情况:
(1),即的三边长分别为2,3,9;由三角形的三边关系可知不合题意,舍去.
(2),即的三边长分别为2,1,19;由三角形的三边关系可知不合题意,舍去.
(3),即的三边长分别为2,7,4;由三角形的三边关系可知不合题意,舍去.
(4),即的三边长分别为5,3,4;即,.
(5),即的三边长分别为5,1,9;由三角形的三边关系可知不合题意,舍去.
(6),即的三边长分别为11,1,4;由三角形的三边关系可知不合题意,舍去.
(7),即的三边长分别为2,4,15;由三角形的三边关系可知不合题意,舍去.
综上可知,的周长为12.
故答案为12.
13.(3分)将几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式例如,由图(1)可得等式:.将图(2)所示的卡片若干张进行拼图,可以将二次三项式分解因式为 .
【解答】解:,
画图如下:
故答案是:.
14.(3分)若,则的值为 3 .
【解答】解:,
,
解得:,,
则,
故答案为:3.
15.(3分)在日常生活中如取款、上网等都需要密码,有一种用“因式分解法”产生的密码,方便记忆,原理是对于多项,因式分解的结果是,若取,时,则各个因式的值是:,,,于是就可以把“180162”作为一个六位数的密码,对于多项式,取,时,用上述方法产生的密码是 104020(答案不唯一) (写出一个即可).
【解答】解:,
当,时,密码可以是104020或102040等等都可以,答案不唯一.
三.解答题(共7小题,满分55分)
16.(8分)分解因式:
(1);
(2);
(3);
(4).
【解答】解:(1)原式;
(2)原式
;
(3)原式
;
(4)原式
.
17.(7分)给出三个多项式:,,.请选择你最喜欢的两个多项式进行加法运算,并把结果因式分解.
【解答】解:情况一:.
情况二:.
情况三:.
18.(8分)对于任意自然数,代数式的值都能被4整除吗?请说明理由.
【解答】解:能被4整除.
理由:原式,
为自然数,
与两数必有一数为偶数,
是4的倍数,
对于任意自然数,代数式的值都能被4整除.
19.(8分)阅读某同学对多项式进行因式分解的过程,并解决问题:
解:设,
原式(第一步)
(第二步)
(第三步)
(第四步)
(1)该同学第二步到第三步的变形运用了 (填序号);
.提公因式法 .平方差公式
.两数和的平方公式 .两数差的平方公式
(2)该同学在第三步用所设的代数式进行了代换,得到第四步的结果,这个结果能否进一步因式分解? (填“能”或“不能” .如果能,直接写出最后结果 .
(3)请你模仿以上方法尝试对多项式进行因式分行解.
【解答】解:(1)该同学第二步到第三步的变形运用了两数和的平方公式,
故选;
(2)该同学在第三步用所设的代数式进行了代换,得到第四步的结果,这个结果能进一步因式分解,
最后结果,
故答案为 能,;
(3)设
.
20.(8分)阅读材料:若,求、的值.
解:,
,,,,.
根据你的观察,探究下面的问题:
(1)已知,求的值;
(2)已知,,求的值.
【解答】解:(1),
,
,
,,
解得,,,
;
(2),
,
将代入,得
,
,
,
,,
解得,,,
,
.
21.(8分)仔细阅读下面例题,解答问题:
例题:已知二次三项式有一个因式是,求另一个因式以及的值.
解:设另一个因式为,得
则
解得:,
另一个因式为,的值为
问题:仿照以上方法解答下面问题:
已知二次三项式有一个因式是,求另一个因式以及的值.
【解答】解:设另一个因式为,得:
,
则,
,
解得:,,
故另一个因式为,的值为20.
22.(8分)阅读下列材料并解答问题:
数学中有很多恒等式可以用图形的面积来得到.例如,图1中阴影部分的面积可表示为;若将阴影部分剪下来,重新拼成一个矩形(如图,它的长,宽分别是,,由图1,图2中阴影部分的面积相等,可得恒等式.
(1)观察图3,根据图形,写出一个代数恒等式: ;
(2)现有若干块长方形和正方形硬纸片如图4所示.请你仿照图3,用拼图的方法分解因式,并画出拼图验证所得的图形.
【解答】解,(1)由图3知,等式为.
(2)
如图:
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
