沪科版数学七年级下册 10.4 平移 教案
文档属性
| 名称 | 沪科版数学七年级下册 10.4 平移 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 50.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-17 20:05:43 | ||
图片预览

文档简介
第十章 相交线与平行线
10.4 平移
【教学目标】
知识与技能
通过回忆生活中物体(图形)的平行移动,经历物体(图形)平移的操作,理解平移的性质。
能够按要求对一个图形进行平移,并运用平移的知识解决问题。
过程与方法
经历操作、探究、归纳、总结图形平移的基本特征的过程,发展学生的抽象概况能力。
情感、态度与价值观
提高学生的动手能力,发展初步的审美能力增强对图形的欣赏意识。
【教学重难点】
重点:平移的性质
难点:平移性质的运用,找对应点和对应线段。
【导学过程】
【情景导入】
播放美丽的图案.观察这些图案、思考并回答问题.
(1)它们有什么共同的特点?
(2)能否根据其中的一部分绘制出整个图案?
回忆本章作平行线时的操作方法,从物体的平移转移到平面图形的平移。并归纳平移的概念和对应点、对应线段、对应角的概念。
【新知探究】
一、平移的概念
(
A
B
C
A’
B’
C’
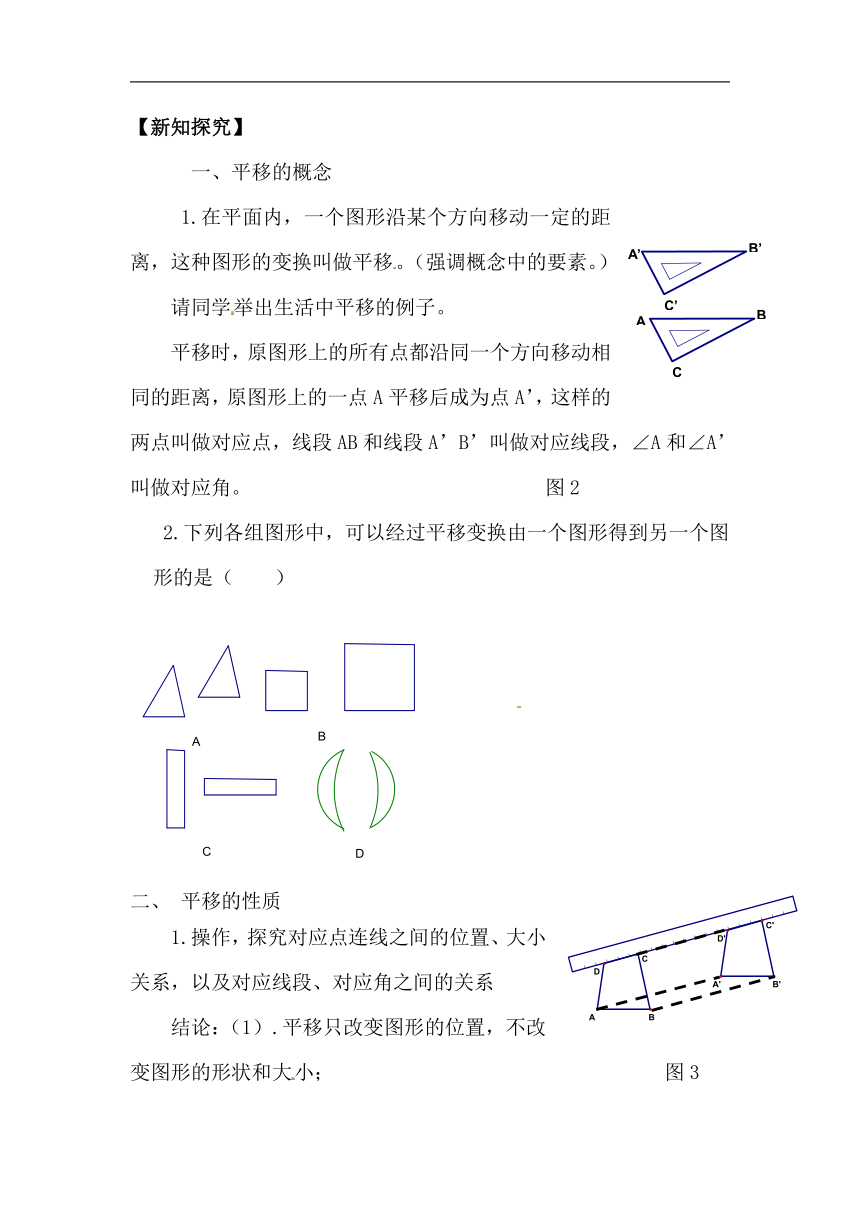
)1.在平面内,一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移。(强调概念中的要素。)
请同学举出生活中平移的例子。
平移时,原图形上的所有点都沿同一个方向移动相同的距离,原图形上的一点A平移后成为点A’,这样的两点叫做对应点,线段AB和线段A’B’叫做对应线段,∠A和∠A’叫做对应角。 图2
2.下列各组图形中,可以经过平移变换由一个图形得到另一个图形的是( )
二、 平移的性质
1.操作,探究对应点连线之间的位置、大小关系,以及对应线段、对应角之间的关系
结论:(1).平移只改变图形的位置,不改变图形的形状和大小; 图3[来
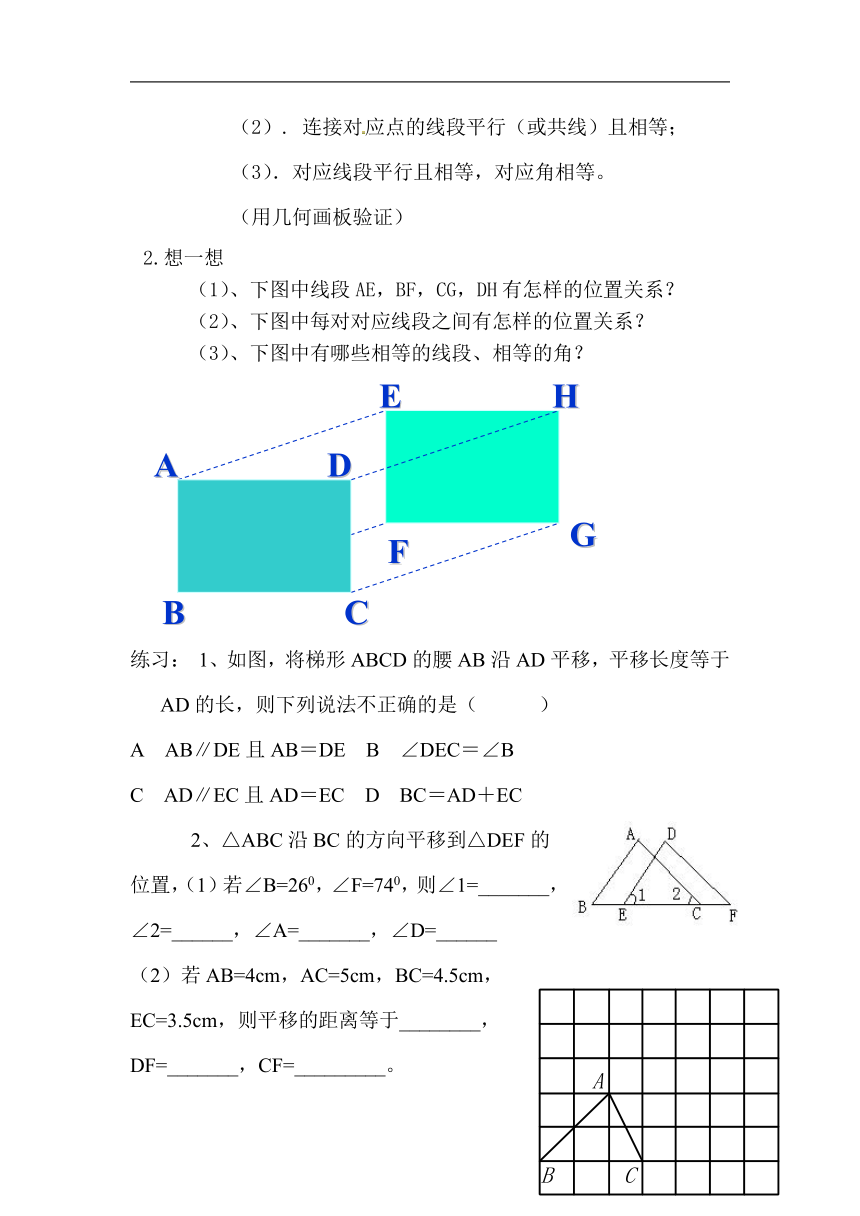
(2). 连接对应点的线段平行(或共线)且相等;
(3).对应线段平行且相等,对应角相等。
(用几何画板验证)
2.想一想
(1)、下图中线段AE,BF,CG,DH有怎样的位置关系?
(2)、下图中每对对应线段之间有怎样的位置关系?
(3)、下图中有哪些相等的线段、相等的角?
(
E
F
G
H
A
C
B
D
)
练习: 1、如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )
A AB∥DE且AB=DE B ∠DEC=∠B
C AD∥EC且AD=EC D BC=AD+EC
2、△ABC沿BC的方向平移到△DEF的位置,(1)若∠B=260,∠F=740,则∠1=_______,
∠2=______,∠A=_______,∠D=______
(2)若AB=4cm,AC=5cm,BC=4.5cm,EC=3.5cm,则平移的距离等于________,DF=_______,CF=_________。
探究三、平移作图
1. 如图4,三角形A1B1C1是将三角形ABC平移后得到的图形,其中A1点是A点的对应点。请找出点D1在三角形ABC中的对应点
作法略
2.(投影几幅大小不一的图片)这些图片能由一幅图片平移得到吗? 图4
它们的形状相同吗?大小相同吗?
3.如图5,将图中的小船向左平移四格。
第一次平移两船之间相距四格,第二次正确。注意应该通过找对应点的方法来判断。 图5
4.如图6,将AB平移,使A移到A1。
5.进一步研究;三角形该如何平移。
如图(4)-1,平移三角形ABC,使点A移动到点A′.画出平移后的三角形A′B′C′.
【知识梳理】
本节课你学到了什么?有什么收获和体会?还有什么困惑?
1、平移定义:在平面内,将一个图形沿某个方向___一定的距离,这样的图形运动称为平移,平移改变的是图形的_____。
注意:①图形的平移是由_____和_____决定的。
②平移的方向不一定水平。
2、平移性质:①平移不改变图形的____和____。
②经过平移所得的图形与原来的图形的对应线段_______,对应角____,对应点所连的线段____。
【随堂练习】
1、(1)如图1,△ABC平移到△DEF,图中
相等的线段有_____________,相等的角有____________,平行的线段有______________。
(2)把一个△ABC沿东南方向平移3cm,则AB边上的中点P沿___方向平移了__cm。
(3)如图,△ABC是由四个形状大小相同的三角形拼成的,则可以看成是△ADF平移得到的小三角形是___________。
(4)如图,△DEF是由△ABC先向右平移__格,再向___平移___格而得到的。
(5)如图,△ABC是由△CEF平移而得,图中有哪些相等的线段?相等的角?
(
C
A
B
F
E
)
10.4 平移
【教学目标】
知识与技能
通过回忆生活中物体(图形)的平行移动,经历物体(图形)平移的操作,理解平移的性质。
能够按要求对一个图形进行平移,并运用平移的知识解决问题。
过程与方法
经历操作、探究、归纳、总结图形平移的基本特征的过程,发展学生的抽象概况能力。
情感、态度与价值观
提高学生的动手能力,发展初步的审美能力增强对图形的欣赏意识。
【教学重难点】
重点:平移的性质
难点:平移性质的运用,找对应点和对应线段。
【导学过程】
【情景导入】
播放美丽的图案.观察这些图案、思考并回答问题.
(1)它们有什么共同的特点?
(2)能否根据其中的一部分绘制出整个图案?
回忆本章作平行线时的操作方法,从物体的平移转移到平面图形的平移。并归纳平移的概念和对应点、对应线段、对应角的概念。
【新知探究】
一、平移的概念
(
A
B
C
A’
B’
C’
)1.在平面内,一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移。(强调概念中的要素。)
请同学举出生活中平移的例子。
平移时,原图形上的所有点都沿同一个方向移动相同的距离,原图形上的一点A平移后成为点A’,这样的两点叫做对应点,线段AB和线段A’B’叫做对应线段,∠A和∠A’叫做对应角。 图2
2.下列各组图形中,可以经过平移变换由一个图形得到另一个图形的是( )
二、 平移的性质
1.操作,探究对应点连线之间的位置、大小关系,以及对应线段、对应角之间的关系
结论:(1).平移只改变图形的位置,不改变图形的形状和大小; 图3[来
(2). 连接对应点的线段平行(或共线)且相等;
(3).对应线段平行且相等,对应角相等。
(用几何画板验证)
2.想一想
(1)、下图中线段AE,BF,CG,DH有怎样的位置关系?
(2)、下图中每对对应线段之间有怎样的位置关系?
(3)、下图中有哪些相等的线段、相等的角?
(
E
F
G
H
A
C
B
D
)
练习: 1、如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )
A AB∥DE且AB=DE B ∠DEC=∠B
C AD∥EC且AD=EC D BC=AD+EC
2、△ABC沿BC的方向平移到△DEF的位置,(1)若∠B=260,∠F=740,则∠1=_______,
∠2=______,∠A=_______,∠D=______
(2)若AB=4cm,AC=5cm,BC=4.5cm,EC=3.5cm,则平移的距离等于________,DF=_______,CF=_________。
探究三、平移作图
1. 如图4,三角形A1B1C1是将三角形ABC平移后得到的图形,其中A1点是A点的对应点。请找出点D1在三角形ABC中的对应点
作法略
2.(投影几幅大小不一的图片)这些图片能由一幅图片平移得到吗? 图4
它们的形状相同吗?大小相同吗?
3.如图5,将图中的小船向左平移四格。
第一次平移两船之间相距四格,第二次正确。注意应该通过找对应点的方法来判断。 图5
4.如图6,将AB平移,使A移到A1。
5.进一步研究;三角形该如何平移。
如图(4)-1,平移三角形ABC,使点A移动到点A′.画出平移后的三角形A′B′C′.
【知识梳理】
本节课你学到了什么?有什么收获和体会?还有什么困惑?
1、平移定义:在平面内,将一个图形沿某个方向___一定的距离,这样的图形运动称为平移,平移改变的是图形的_____。
注意:①图形的平移是由_____和_____决定的。
②平移的方向不一定水平。
2、平移性质:①平移不改变图形的____和____。
②经过平移所得的图形与原来的图形的对应线段_______,对应角____,对应点所连的线段____。
【随堂练习】
1、(1)如图1,△ABC平移到△DEF,图中
相等的线段有_____________,相等的角有____________,平行的线段有______________。
(2)把一个△ABC沿东南方向平移3cm,则AB边上的中点P沿___方向平移了__cm。
(3)如图,△ABC是由四个形状大小相同的三角形拼成的,则可以看成是△ADF平移得到的小三角形是___________。
(4)如图,△DEF是由△ABC先向右平移__格,再向___平移___格而得到的。
(5)如图,△ABC是由△CEF平移而得,图中有哪些相等的线段?相等的角?
(
C
A
B
F
E
)
