2021-2022学年鲁教版(五四制)数学 六年级下册第7章 相交线与平行线 单元测试卷(word版、含解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)数学 六年级下册第7章 相交线与平行线 单元测试卷(word版、含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 113.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-17 20:35:50 | ||
图片预览



文档简介
2021-2022学年鲁教五四新版六年级下册数学《第7章 相交线与平行线》单元测试卷
一.选择题(共8小题,满分32分)
1.如图,从A到B有多条道路,人们往往走中间的直路,而不会走其他的曲折的路,这是因为( )
A.两条直线相交只有一个交点
B.两点之间线段最短
C.两点确定一条直线
D.其他的路行不通
2.若P,Q是直线AB外不重合的两点,则下列说法不正确的是( )
A.直线PQ可能与直线AB垂直
B.直线PQ可能与直线AB平行
C.过点P的直线一定与直线AB相交
D.过点Q只能画出一条直线与直线AB平行
3.如图,直线AB与CD相交于点P,F是∠APD内的一点,已知FP⊥AB于P,且∠FPD=50°,则∠CPA的度数是( )
A.30° B.40° C.50° D.60°
4.如图,平行线AB,CD被直线MN所截,交点为E,F,且HE⊥MN,若∠HEB=40°,则∠DFN的度数为( )
A.30° B.40° C.50° D.60°
5.如图,直线AB、CD、EF相交于点O,∠1的邻补角是( )
A.∠BOC B.∠BOC和∠AOF C.∠AOF D.∠BOE和∠AOF
6.如图,点E在CD的延长线上,下列条件中能判定AB∥CD的是( )
A.∠C=∠5 B.∠C+∠BDC=180°
C.∠1=∠2 D.∠3=∠4
7.下列说法中,正确的个数为( )
(1)过一点有无数条直线与已知直线平行
(2)如果a∥b,a∥c,那么b∥c
(3)如果两线段不相交,那么它们就平行
(4)如果两直线不相交,那么它们就平行
A.1个 B.2个 C.3个 D.4个
8.在下列各题中,属于尺规作图的是( )
A.用直尺画一工件边缘的垂线
B.用直尺和三角板画平行线
C.利用三角板画45°的角
D.用圆规在已知直线上截取一条线段等于已知线段
二.填空题(共8小题,满分32分)
9.对顶角的性质: ;邻补角的性质: .
10.下列语句是有关几何作图的叙述.
①以O为圆心作弧;②延长射线AB到点C;③作∠AOB,使∠AOB=∠1;④作直线AB,使AB=a;⑤过三角形ABC的顶点C作它的对边AB的平行线.其中正确的有 .(填序号即可)
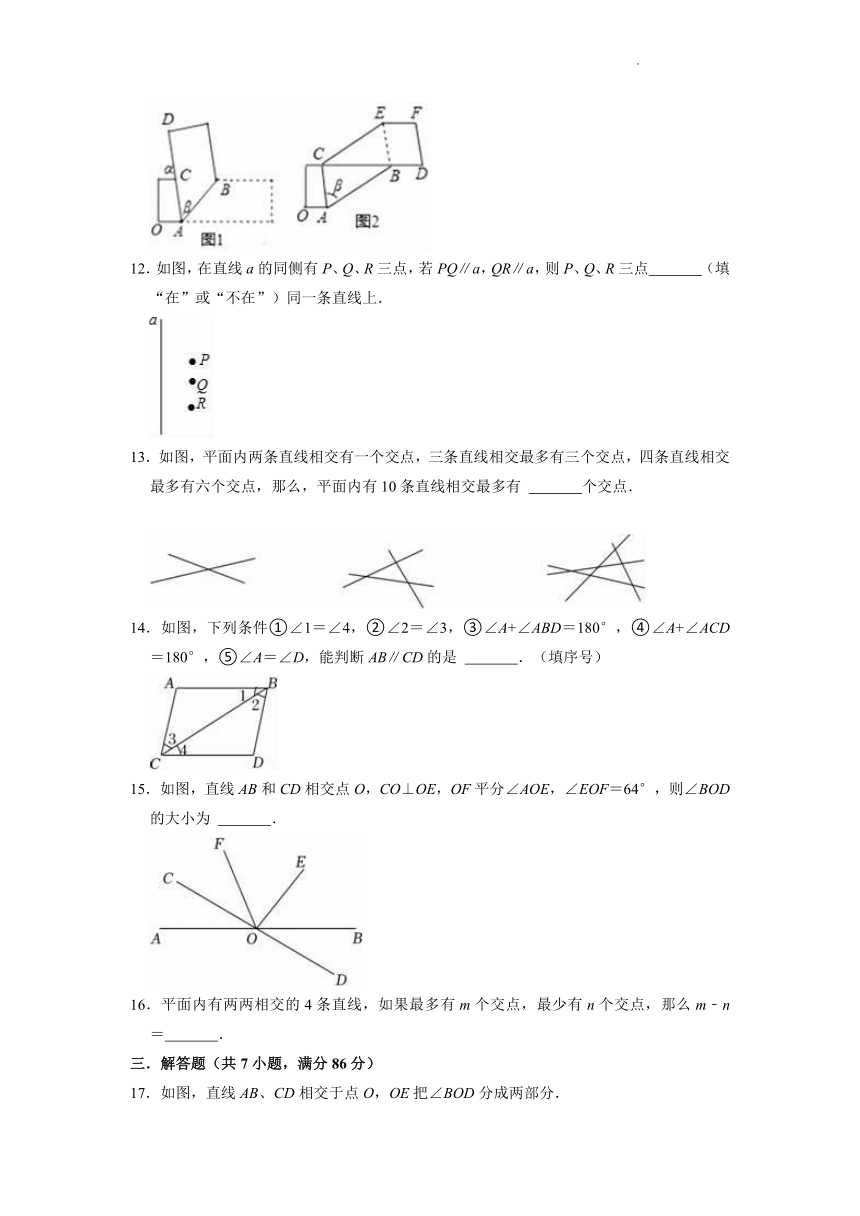
11.如图1,将一条两边互相平行的纸袋折叠.
(1)若图中α=70°,则β= °
(2)在图1的基础上继续折叠,使得图1中的CD边与CB边重合(如图2),若继续沿CB边折叠,CE边恰好平分∠ACB,则此时β的度数为 度.
12.如图,在直线a的同侧有P、Q、R三点,若PQ∥a,QR∥a,则P、Q、R三点 (填“在”或“不在”)同一条直线上.
13.如图,平面内两条直线相交有一个交点,三条直线相交最多有三个交点,四条直线相交最多有六个交点,那么,平面内有10条直线相交最多有 个交点.
14.如图,下列条件①∠1=∠4,②∠2=∠3,③∠A+∠ABD=180°,④∠A+∠ACD=180°,⑤∠A=∠D,能判断AB∥CD的是 .(填序号)
15.如图,直线AB和CD相交点O,CO⊥OE,OF平分∠AOE,∠EOF=64°,则∠BOD的大小为 .
16.平面内有两两相交的4条直线,如果最多有m个交点,最少有n个交点,那么m﹣n= .
三.解答题(共7小题,满分86分)
17.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.
(1)直接写出图中∠BOD的对顶角为 ,∠DOE的邻补角为 ;
(2)若∠AOC=80°,且∠BOE:∠EOD=2:3,求∠AOE的度数.
18.如图,直线AB、CD相交于点O,OE平分∠BOD,OE⊥OF.
(1)若∠DOE=32°,求∠BOF的度数;
(2)若∠COE:∠COF=8:3,求∠AOF的度数.
19.如图,AB∥CD,CD∥EF,BC∥ED,∠B=70°,求∠C,∠D和∠E的度数.
20.如图,AB∥EF∥CD,∠ABC=54°,∠CEF=142°,求∠BCE的度数.
21.同一平面内1条直线把平面分成两个部分(或区域);2条直线最多可将平面分成几个部分?3条直线最多可将平面分成几个部分?4条直线最多可将平面分成几个部分?请分别画出图来.由此可知n条直线最多可将平面分成几个部分?
22.作图题:(只保留作图痕迹)如图,在方格纸中,有两条线段AB、BC.利用方格纸完成以下操作:
(1)过点A作BC的平行线;
(2)过点C作AB的平行线,与(1)中的平行线交于点D;
(3)过点B作AB的垂线.
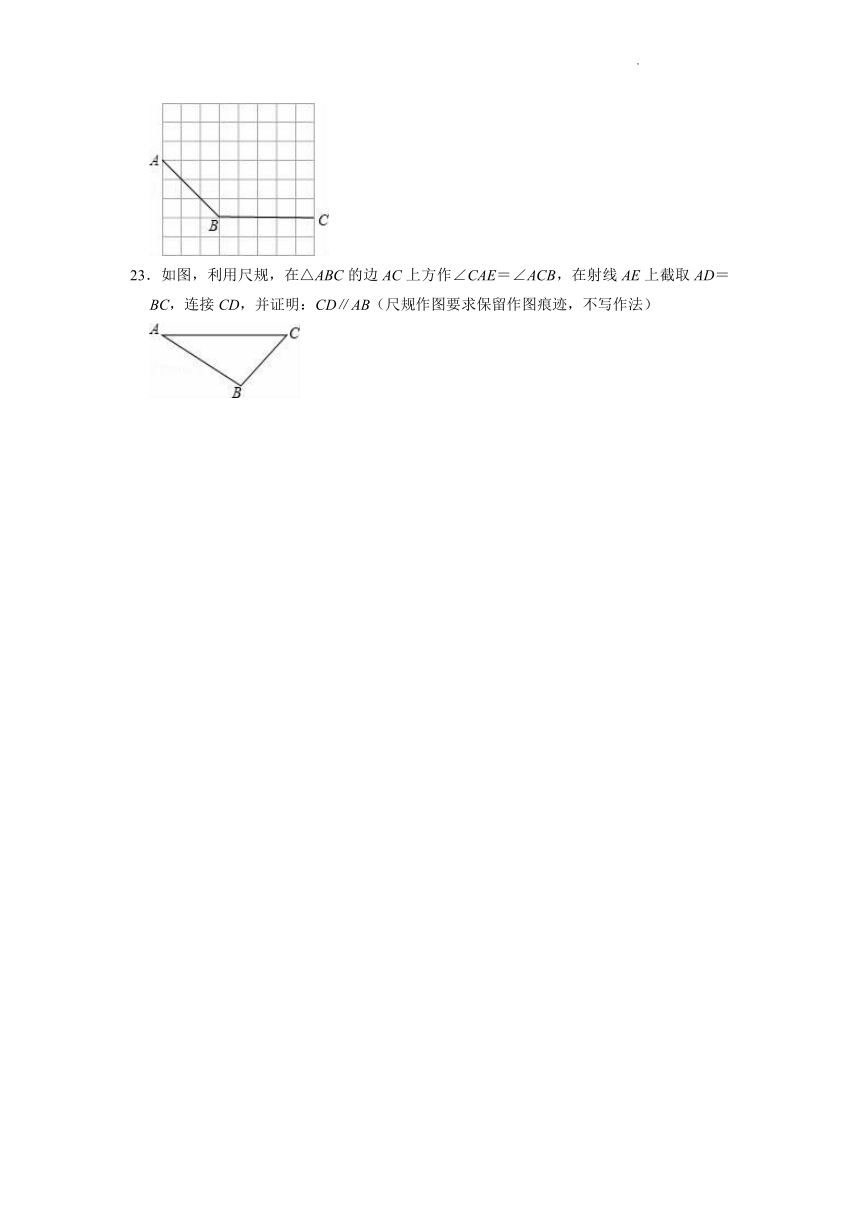
23.如图,利用尺规,在△ABC的边AC上方作∠CAE=∠ACB,在射线AE上截取AD=BC,连接CD,并证明:CD∥AB(尺规作图要求保留作图痕迹,不写作法)
参考答案与试题解析
一.选择题(共8小题,满分32分)
1.解:从A到B有多条道路,人们会走中间的直路,而不会走其他曲折的路,这是因为两点之间,线段最短.
故选:B.
2.解:PQ与直线AB可能平行,也可能垂直,过直线外一点有且只有一条直线与已知直线平行,故A、B、D均正确,
故C错误;
故选:C.
3.解:∵FP⊥AB,
∴∠APF=90°,
∵∠FPD=50°,
∴∠DPB=180°﹣∠APF﹣∠FPD=40°,
∴∠CPA=∠DPB=40°,
故选:B.
4.解:∵HE⊥MN,
∴∠HEN=90°,
∵∠HEB=40°,
∴∠BEN=∠HEN﹣∠HEB=90°﹣40°=50°,
∵AB∥CD,
∴∠DFN=∠BEN=50°,
故选:C.
5.解:因为构成∠1的两边与直线AB和EF有关;
从直线AB来看,∠1的邻补角是∠EOB,
从直线EF来看,∠1的邻补角是∠AOF,
∴∠1的邻补角有∠EOB,∠AOF,
故选:D.
6.解:A、当∠C=∠5时,可得:AC∥BD,不合题意;
B、当∠C+∠BDC=180°时,可得:AC∥BD,不合题意;
C、当∠1=∠2时,可得:AC∥BD,不合题意;
D、当∠3=∠4时,可得:AB∥CD,符合题意.
故选:D.
7.解:(1)过直线外一点有且只有一条直线与已知直线平行,故错误;
(2)根据平行公理的推论,正确;
(3)线段的长度是有限的,不相交也不一定平行,故错误;
(4)应该是“在同一平面内”,故错误.
正确的只有一个,故选A.
8.解:A、用直尺画一工件边缘的垂线,不属于尺规作图;
B、用直尺和三角板画平行线,不属于尺规作图;
C、利用三角板画45°的角,不属于尺规作图;
D、用圆规在已知直线上截取一条线段等于已知线段,属于尺规作图.
故选:D.
二.填空题(共8小题,满分32分)
9.解:对顶角的性质:对顶角相等
邻补角的性质:邻补角之和等于180°,
故答案为:邻补角之和等于180°.
10.解:①以O为圆心作弧可以画出无数条弧,因为半径不固定,所以叙述错误;
②射线AB是由A向B向无限延伸,所以叙述错误;
③根据作一个角等于已知角的作法,可以作一个角∠AOB,使∠AOB等于已知∠1,所以叙述正确;
④直线可以向两方无限延伸,所以叙述错误;
⑤根据平行公理:过直线外一点有且只有一条直线与已知直线平行,可以过三角形ABC的顶点C作它的对边AB的平行线,所以叙述正确.
所以正确的有③⑤.
故答案为:③⑤.
11.解:(1)根据上下边互相平行可知,α=∠OAD,
∵α=70°,
∴∠OAD=70°.
又∠OAD+2β=180°,
∴β=55°.
故答案为:55.
(2)根据折叠的性质可知,折叠两次后形成的三个角都相等,
根据题意可知,折叠两次后形成的三个角与折叠后的∠ACE都相等,而这四个角的和为180°,故每个角为45°,
∴∠ACB=90°,即α=90°,
由(1)中可得,β=(180°﹣90°)=45°.
故答案为:45.
12.解:∵PQ∥a,QR∥a(已知),
∴P,Q,R三点在同一条直线上(过直线外一点有且只有一条直线与已知直线平行),
故答案为:在.
13.解:两条直线相交最多有1个交点,
三条直线相交最多有1+2=3个交点,
四条直线相交最多有1+2+3=6个交点,
……
十条直线相交最多有1+2+3+4+5+6+7+8+9=45个交点,
故答案为:45.
14.解:①若∠1=∠4,则AB∥CD,符合题意;
②若∠2=∠3,则AC∥BD,不符合题意;
③若∠A+∠ABD=180°,则AC∥BD,不符合题意;
④若∠A+∠ACD=180°,则AB∥CD,符合题意;
⑤若∠A=∠D,无法得到AB∥CD,不符合题意.
故能判断AB∥CD的是①④.
故答案为:①④.
15.解:∵CO⊥OE,
∴∠COE=90°,
∵∠EOF=64°,
∴∠COF=26°,
OF平分∠AOE,
∴∠AOF=∠EOF=64°,
∴∠AOC=64°﹣26°=38°,
∵∠AOC与∠BOD是对顶角,
∴∠BOD=38°.
故答案为:38°.
16.解:如图所示:
4条直线两两相交,有3种情况:4条直线经过同一点,有一个交点;3条直线经过同一点,被第4条直线所截,有4个交点;4条直线不经过同一点,有6个交点.
故平面内两两相交的4条直线,最多有6个交点,最少有1个交点;即m=6,n=1,则m﹣n=5.
故答案为:5.
三.解答题(共7小题,满分86分)
17.解:(1)∠BOD的对顶角为∠AOC,∠DOE的邻补角为∠EOC,
故答案为:∠AOC,∠EOC;
(2)∵∠AOC=80°,
∴∠BOD=80°,∠AOD=180°﹣80°=100°,
又∵∠BOE:∠EOD=2:3,
∴∠DOE=80°×=48°,
∴∠AOE=∠AOD+∠DOE
=100°+48°
=148°,
答:∠AOE的度数为148°.
18.解:(1)∵OE平分∠BOD,
∴∠DOE=∠EOB,
∵∠DOE=32°,
∴∠EOB=32°,
∵OE⊥OF,
∴∠EOF=90°,
∴∠BOF=∠EOF﹣∠EOB=90°﹣32°=58°;
(2)∵∠COE:∠COF=8:3,
∴设∠COE=8x,∠COF=3x,
∴∠EOF=5x,
∵OE⊥OF,
∴∠EOF=90°,
∵5x=90°,
∴x=18°,
∴∠COF=3x=54°,
∴∠DOE=180°﹣∠COF﹣∠FOE=180°﹣54°﹣90°=36°,
∵OE平分∠BOD,
∴∠DOB=72°,
∴∠AOC=72°,
∴∠AOF=∠AOC+∠COF=72°+54°=126°.
19.解:∵AB∥CD,CD∥EF,
∴AB∥CD∥EF,
∴∠C=∠B=70°,∠E=∠D,
又∵BC∥DE,
∴∠C+∠D=180°,
∴∠B+∠E=180°,
∴∠E=110°.
答:∠C,∠D和∠E的度数分别是70°、110°、110°.
20.解:∵AB∥CD,
∴∠ABC=∠BCD=54°,
∵EF∥CD,
∴∠CEF+∠ECD=180°,
∵∠CEF=142°,
∴∠ECD=38°,
∴∠BCE=∠BCD﹣∠ECD=54°﹣38°=16°.
21.解:2条直线最多可将平面分成4个部分,如图:;
三条直线最多分成可将平面分成7个部分,如图:;
四条直线最多分成可将平面分成11个部分,如图:;
n条直线最多分成可将平面分成2+2+3+4+…+n=个部分.
22.解:如图,
(1)A所在的横线就是满足条件的直线,即AE就是所求;
(2)在直线AE上,到A距离是5个格长的点就是D,则CD就是所求与AB平行的直线;
(3)取AE上D右边的点F,过B,F作直线,就是所求.
23.解:图象如图所示,
∵∠EAC=∠ACB,
∴AD∥CB,
∵AD=BC,∠DAC=∠ACB,AC=CA,
∴△ACD≌△CAB(SAS),
∴∠ACD=∠CAB,
∴AB∥CD.
一.选择题(共8小题,满分32分)
1.如图,从A到B有多条道路,人们往往走中间的直路,而不会走其他的曲折的路,这是因为( )
A.两条直线相交只有一个交点
B.两点之间线段最短
C.两点确定一条直线
D.其他的路行不通
2.若P,Q是直线AB外不重合的两点,则下列说法不正确的是( )
A.直线PQ可能与直线AB垂直
B.直线PQ可能与直线AB平行
C.过点P的直线一定与直线AB相交
D.过点Q只能画出一条直线与直线AB平行
3.如图,直线AB与CD相交于点P,F是∠APD内的一点,已知FP⊥AB于P,且∠FPD=50°,则∠CPA的度数是( )
A.30° B.40° C.50° D.60°
4.如图,平行线AB,CD被直线MN所截,交点为E,F,且HE⊥MN,若∠HEB=40°,则∠DFN的度数为( )
A.30° B.40° C.50° D.60°
5.如图,直线AB、CD、EF相交于点O,∠1的邻补角是( )
A.∠BOC B.∠BOC和∠AOF C.∠AOF D.∠BOE和∠AOF
6.如图,点E在CD的延长线上,下列条件中能判定AB∥CD的是( )
A.∠C=∠5 B.∠C+∠BDC=180°
C.∠1=∠2 D.∠3=∠4
7.下列说法中,正确的个数为( )
(1)过一点有无数条直线与已知直线平行
(2)如果a∥b,a∥c,那么b∥c
(3)如果两线段不相交,那么它们就平行
(4)如果两直线不相交,那么它们就平行
A.1个 B.2个 C.3个 D.4个
8.在下列各题中,属于尺规作图的是( )
A.用直尺画一工件边缘的垂线
B.用直尺和三角板画平行线
C.利用三角板画45°的角
D.用圆规在已知直线上截取一条线段等于已知线段
二.填空题(共8小题,满分32分)
9.对顶角的性质: ;邻补角的性质: .
10.下列语句是有关几何作图的叙述.
①以O为圆心作弧;②延长射线AB到点C;③作∠AOB,使∠AOB=∠1;④作直线AB,使AB=a;⑤过三角形ABC的顶点C作它的对边AB的平行线.其中正确的有 .(填序号即可)
11.如图1,将一条两边互相平行的纸袋折叠.
(1)若图中α=70°,则β= °
(2)在图1的基础上继续折叠,使得图1中的CD边与CB边重合(如图2),若继续沿CB边折叠,CE边恰好平分∠ACB,则此时β的度数为 度.
12.如图,在直线a的同侧有P、Q、R三点,若PQ∥a,QR∥a,则P、Q、R三点 (填“在”或“不在”)同一条直线上.
13.如图,平面内两条直线相交有一个交点,三条直线相交最多有三个交点,四条直线相交最多有六个交点,那么,平面内有10条直线相交最多有 个交点.
14.如图,下列条件①∠1=∠4,②∠2=∠3,③∠A+∠ABD=180°,④∠A+∠ACD=180°,⑤∠A=∠D,能判断AB∥CD的是 .(填序号)
15.如图,直线AB和CD相交点O,CO⊥OE,OF平分∠AOE,∠EOF=64°,则∠BOD的大小为 .
16.平面内有两两相交的4条直线,如果最多有m个交点,最少有n个交点,那么m﹣n= .
三.解答题(共7小题,满分86分)
17.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.
(1)直接写出图中∠BOD的对顶角为 ,∠DOE的邻补角为 ;
(2)若∠AOC=80°,且∠BOE:∠EOD=2:3,求∠AOE的度数.
18.如图,直线AB、CD相交于点O,OE平分∠BOD,OE⊥OF.
(1)若∠DOE=32°,求∠BOF的度数;
(2)若∠COE:∠COF=8:3,求∠AOF的度数.
19.如图,AB∥CD,CD∥EF,BC∥ED,∠B=70°,求∠C,∠D和∠E的度数.
20.如图,AB∥EF∥CD,∠ABC=54°,∠CEF=142°,求∠BCE的度数.
21.同一平面内1条直线把平面分成两个部分(或区域);2条直线最多可将平面分成几个部分?3条直线最多可将平面分成几个部分?4条直线最多可将平面分成几个部分?请分别画出图来.由此可知n条直线最多可将平面分成几个部分?
22.作图题:(只保留作图痕迹)如图,在方格纸中,有两条线段AB、BC.利用方格纸完成以下操作:
(1)过点A作BC的平行线;
(2)过点C作AB的平行线,与(1)中的平行线交于点D;
(3)过点B作AB的垂线.
23.如图,利用尺规,在△ABC的边AC上方作∠CAE=∠ACB,在射线AE上截取AD=BC,连接CD,并证明:CD∥AB(尺规作图要求保留作图痕迹,不写作法)
参考答案与试题解析
一.选择题(共8小题,满分32分)
1.解:从A到B有多条道路,人们会走中间的直路,而不会走其他曲折的路,这是因为两点之间,线段最短.
故选:B.
2.解:PQ与直线AB可能平行,也可能垂直,过直线外一点有且只有一条直线与已知直线平行,故A、B、D均正确,
故C错误;
故选:C.
3.解:∵FP⊥AB,
∴∠APF=90°,
∵∠FPD=50°,
∴∠DPB=180°﹣∠APF﹣∠FPD=40°,
∴∠CPA=∠DPB=40°,
故选:B.
4.解:∵HE⊥MN,
∴∠HEN=90°,
∵∠HEB=40°,
∴∠BEN=∠HEN﹣∠HEB=90°﹣40°=50°,
∵AB∥CD,
∴∠DFN=∠BEN=50°,
故选:C.
5.解:因为构成∠1的两边与直线AB和EF有关;
从直线AB来看,∠1的邻补角是∠EOB,
从直线EF来看,∠1的邻补角是∠AOF,
∴∠1的邻补角有∠EOB,∠AOF,
故选:D.
6.解:A、当∠C=∠5时,可得:AC∥BD,不合题意;
B、当∠C+∠BDC=180°时,可得:AC∥BD,不合题意;
C、当∠1=∠2时,可得:AC∥BD,不合题意;
D、当∠3=∠4时,可得:AB∥CD,符合题意.
故选:D.
7.解:(1)过直线外一点有且只有一条直线与已知直线平行,故错误;
(2)根据平行公理的推论,正确;
(3)线段的长度是有限的,不相交也不一定平行,故错误;
(4)应该是“在同一平面内”,故错误.
正确的只有一个,故选A.
8.解:A、用直尺画一工件边缘的垂线,不属于尺规作图;
B、用直尺和三角板画平行线,不属于尺规作图;
C、利用三角板画45°的角,不属于尺规作图;
D、用圆规在已知直线上截取一条线段等于已知线段,属于尺规作图.
故选:D.
二.填空题(共8小题,满分32分)
9.解:对顶角的性质:对顶角相等
邻补角的性质:邻补角之和等于180°,
故答案为:邻补角之和等于180°.
10.解:①以O为圆心作弧可以画出无数条弧,因为半径不固定,所以叙述错误;
②射线AB是由A向B向无限延伸,所以叙述错误;
③根据作一个角等于已知角的作法,可以作一个角∠AOB,使∠AOB等于已知∠1,所以叙述正确;
④直线可以向两方无限延伸,所以叙述错误;
⑤根据平行公理:过直线外一点有且只有一条直线与已知直线平行,可以过三角形ABC的顶点C作它的对边AB的平行线,所以叙述正确.
所以正确的有③⑤.
故答案为:③⑤.
11.解:(1)根据上下边互相平行可知,α=∠OAD,
∵α=70°,
∴∠OAD=70°.
又∠OAD+2β=180°,
∴β=55°.
故答案为:55.
(2)根据折叠的性质可知,折叠两次后形成的三个角都相等,
根据题意可知,折叠两次后形成的三个角与折叠后的∠ACE都相等,而这四个角的和为180°,故每个角为45°,
∴∠ACB=90°,即α=90°,
由(1)中可得,β=(180°﹣90°)=45°.
故答案为:45.
12.解:∵PQ∥a,QR∥a(已知),
∴P,Q,R三点在同一条直线上(过直线外一点有且只有一条直线与已知直线平行),
故答案为:在.
13.解:两条直线相交最多有1个交点,
三条直线相交最多有1+2=3个交点,
四条直线相交最多有1+2+3=6个交点,
……
十条直线相交最多有1+2+3+4+5+6+7+8+9=45个交点,
故答案为:45.
14.解:①若∠1=∠4,则AB∥CD,符合题意;
②若∠2=∠3,则AC∥BD,不符合题意;
③若∠A+∠ABD=180°,则AC∥BD,不符合题意;
④若∠A+∠ACD=180°,则AB∥CD,符合题意;
⑤若∠A=∠D,无法得到AB∥CD,不符合题意.
故能判断AB∥CD的是①④.
故答案为:①④.
15.解:∵CO⊥OE,
∴∠COE=90°,
∵∠EOF=64°,
∴∠COF=26°,
OF平分∠AOE,
∴∠AOF=∠EOF=64°,
∴∠AOC=64°﹣26°=38°,
∵∠AOC与∠BOD是对顶角,
∴∠BOD=38°.
故答案为:38°.
16.解:如图所示:
4条直线两两相交,有3种情况:4条直线经过同一点,有一个交点;3条直线经过同一点,被第4条直线所截,有4个交点;4条直线不经过同一点,有6个交点.
故平面内两两相交的4条直线,最多有6个交点,最少有1个交点;即m=6,n=1,则m﹣n=5.
故答案为:5.
三.解答题(共7小题,满分86分)
17.解:(1)∠BOD的对顶角为∠AOC,∠DOE的邻补角为∠EOC,
故答案为:∠AOC,∠EOC;
(2)∵∠AOC=80°,
∴∠BOD=80°,∠AOD=180°﹣80°=100°,
又∵∠BOE:∠EOD=2:3,
∴∠DOE=80°×=48°,
∴∠AOE=∠AOD+∠DOE
=100°+48°
=148°,
答:∠AOE的度数为148°.
18.解:(1)∵OE平分∠BOD,
∴∠DOE=∠EOB,
∵∠DOE=32°,
∴∠EOB=32°,
∵OE⊥OF,
∴∠EOF=90°,
∴∠BOF=∠EOF﹣∠EOB=90°﹣32°=58°;
(2)∵∠COE:∠COF=8:3,
∴设∠COE=8x,∠COF=3x,
∴∠EOF=5x,
∵OE⊥OF,
∴∠EOF=90°,
∵5x=90°,
∴x=18°,
∴∠COF=3x=54°,
∴∠DOE=180°﹣∠COF﹣∠FOE=180°﹣54°﹣90°=36°,
∵OE平分∠BOD,
∴∠DOB=72°,
∴∠AOC=72°,
∴∠AOF=∠AOC+∠COF=72°+54°=126°.
19.解:∵AB∥CD,CD∥EF,
∴AB∥CD∥EF,
∴∠C=∠B=70°,∠E=∠D,
又∵BC∥DE,
∴∠C+∠D=180°,
∴∠B+∠E=180°,
∴∠E=110°.
答:∠C,∠D和∠E的度数分别是70°、110°、110°.
20.解:∵AB∥CD,
∴∠ABC=∠BCD=54°,
∵EF∥CD,
∴∠CEF+∠ECD=180°,
∵∠CEF=142°,
∴∠ECD=38°,
∴∠BCE=∠BCD﹣∠ECD=54°﹣38°=16°.
21.解:2条直线最多可将平面分成4个部分,如图:;
三条直线最多分成可将平面分成7个部分,如图:;
四条直线最多分成可将平面分成11个部分,如图:;
n条直线最多分成可将平面分成2+2+3+4+…+n=个部分.
22.解:如图,
(1)A所在的横线就是满足条件的直线,即AE就是所求;
(2)在直线AE上,到A距离是5个格长的点就是D,则CD就是所求与AB平行的直线;
(3)取AE上D右边的点F,过B,F作直线,就是所求.
23.解:图象如图所示,
∵∠EAC=∠ACB,
∴AD∥CB,
∵AD=BC,∠DAC=∠ACB,AC=CA,
∴△ACD≌△CAB(SAS),
∴∠ACD=∠CAB,
∴AB∥CD.
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
