2.8相似多边形的性质(2)
图片预览





文档简介
课件16张PPT。相似多边形的性质(2) 忆一忆:什么叫相似多边形?两个多边形的边数相同,各角对应相等、各边对应成比例,
这样的两个多边形叫做相似多边形。相似多边形的对应角相等,对应边成比例。
(1)??相似多边形的周长比、面积比与相似比的关系。
(2)???相似多边形的周长比、面积比在实际中的应用。
(3)???经历探索相似多边形的性质的过程,培养学生
的探索能力。
重点:
相似多边形的周长比、面积比与相似比关系的推导;
运用相似多边形的比例关系解决实际问题。
难点:
相似多边形周长比、面积比与相似比的关系的推导
及运用 .学习目标 ΔABC~ΔA`B`C`, 相似比为3:4。(1)ΔABC和ΔA`B`C`周长比是多少?(2)ΔABC和ΔA`B`C`面积比是多少?思考:相似三角形的性质?相似三角形的周长之比等于相似比,
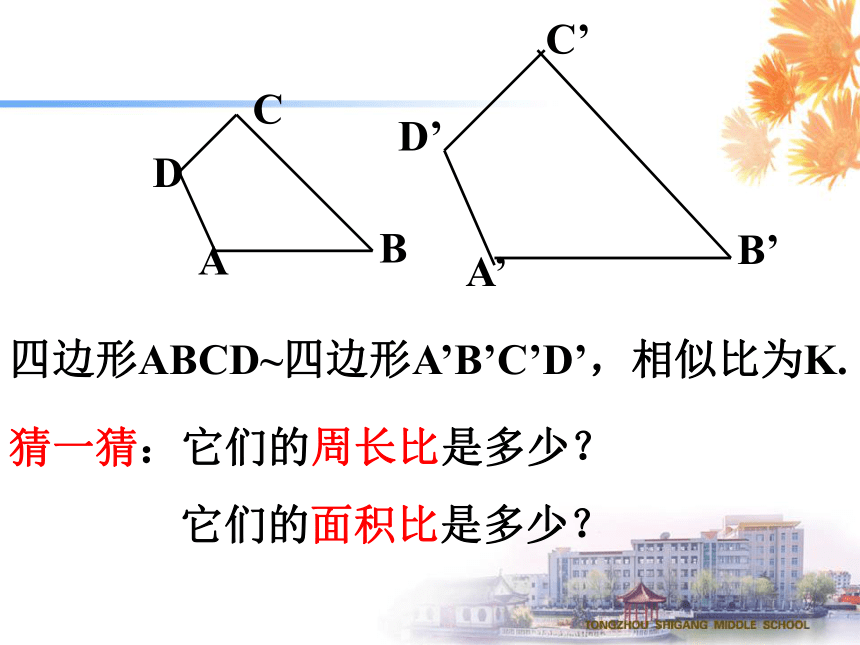
面积之比等于相似比的平方。ACBA’B’C’想一想 如果把三角形换成四边形,刚才的结论是否仍然成立呢?四边形ABCD~四边形A’B’C’D’,相似比为K.ABCDA’B’C’D’猜一猜:它们的周长比是多少?
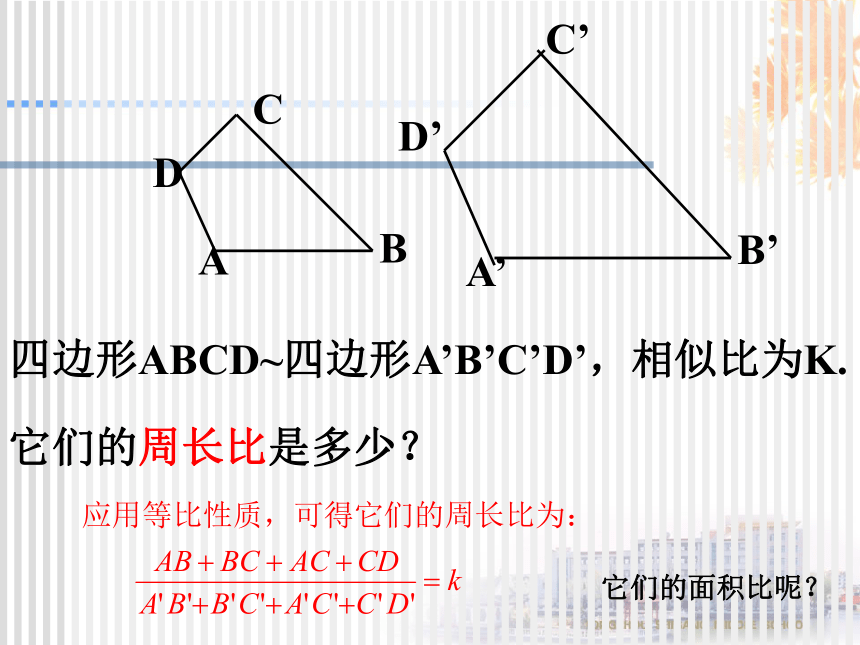
它们的面积比是多少? 四边形ABCD~四边形A’B’C’D’,相似比为K.ABCDA’B’C’D’它们的周长比是多少?它们的面积比呢?合作、交流、探究如果把四边形换成五边形呢?结论是否仍然成立?
n边形呢?结论:相似多边形的周长比等于相似比,面积比等于相似比的平方。做一做在比例尺为1:100000的地图上,某开发区的图上周长为25cm,图上面积为25cm2,那么该开发区的实际周长和实际面积分别是多少?随堂练习:(1)在比例尺为1∶5000的地图上,量得甲、乙两地的距离为25cm,则甲、乙两地间的实际距离是( ).
(A) 1250km (B)125km (C)12.5km (D)1.25km
(2)已知相似多边形的相似比为9∶4,那么这两个多边形的周长比为( ).
(A) 9∶4 (B)4∶9 (C) 3∶2 (D)81∶16
(3)两个相似多边形的面积比为4:9,那么它们周长的比为_ ____ .DA2:3(4)老师在电脑上画了一个六边形,上课时发现,原来一条5厘米的边在电视屏幕上变成了15厘米,那么电视屏幕的放大比例是( ),这个六边形的面积扩大为原来的( )倍。1:39拓展与延伸 公园中的儿童游乐场是两个相似多边形地块,相似比为2:3,面积差为30m2,它们的面积分别是多少?课堂总结:相似多边形的性质:
相似多边形的周长比等于相似比,面积的比等于相似比的平方.学习了本节课,你有哪些收获?课后作业
课本习题2.13
这样的两个多边形叫做相似多边形。相似多边形的对应角相等,对应边成比例。
(1)??相似多边形的周长比、面积比与相似比的关系。
(2)???相似多边形的周长比、面积比在实际中的应用。
(3)???经历探索相似多边形的性质的过程,培养学生
的探索能力。
重点:
相似多边形的周长比、面积比与相似比关系的推导;
运用相似多边形的比例关系解决实际问题。
难点:
相似多边形周长比、面积比与相似比的关系的推导
及运用 .学习目标 ΔABC~ΔA`B`C`, 相似比为3:4。(1)ΔABC和ΔA`B`C`周长比是多少?(2)ΔABC和ΔA`B`C`面积比是多少?思考:相似三角形的性质?相似三角形的周长之比等于相似比,
面积之比等于相似比的平方。ACBA’B’C’想一想 如果把三角形换成四边形,刚才的结论是否仍然成立呢?四边形ABCD~四边形A’B’C’D’,相似比为K.ABCDA’B’C’D’猜一猜:它们的周长比是多少?
它们的面积比是多少? 四边形ABCD~四边形A’B’C’D’,相似比为K.ABCDA’B’C’D’它们的周长比是多少?它们的面积比呢?合作、交流、探究如果把四边形换成五边形呢?结论是否仍然成立?
n边形呢?结论:相似多边形的周长比等于相似比,面积比等于相似比的平方。做一做在比例尺为1:100000的地图上,某开发区的图上周长为25cm,图上面积为25cm2,那么该开发区的实际周长和实际面积分别是多少?随堂练习:(1)在比例尺为1∶5000的地图上,量得甲、乙两地的距离为25cm,则甲、乙两地间的实际距离是( ).
(A) 1250km (B)125km (C)12.5km (D)1.25km
(2)已知相似多边形的相似比为9∶4,那么这两个多边形的周长比为( ).
(A) 9∶4 (B)4∶9 (C) 3∶2 (D)81∶16
(3)两个相似多边形的面积比为4:9,那么它们周长的比为_ ____ .DA2:3(4)老师在电脑上画了一个六边形,上课时发现,原来一条5厘米的边在电视屏幕上变成了15厘米,那么电视屏幕的放大比例是( ),这个六边形的面积扩大为原来的( )倍。1:39拓展与延伸 公园中的儿童游乐场是两个相似多边形地块,相似比为2:3,面积差为30m2,它们的面积分别是多少?课堂总结:相似多边形的性质:
相似多边形的周长比等于相似比,面积的比等于相似比的平方.学习了本节课,你有哪些收获?课后作业
课本习题2.13
