4.3共点力的平衡 同步练习(Word版含解析)
文档属性
| 名称 | 4.3共点力的平衡 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-17 00:00:00 | ||
图片预览



文档简介
鲁科版 (2019)必修一 4.3 共点力的平衡 同步练习
一、单选题
1.日常生活、生产中,常常需要将物体水平移动。一重量为G的物体与水平面间动摩擦因数为0.75,最大静摩擦力等于滑动摩擦力,不计空气阻力,则要使该物体沿该水平面做匀速直线运动的最小拉力为( )
A.0.75G B.0.6G C.0.5G D.0.3G
2.如图所示,V型光滑挡板AOB之间放置有一质量均匀的球体,初始时系统处于静止状态,现将整个装置以O点为轴顺时针缓慢转动(∠AOB保持不变),在AO由水平转动90°到竖直的过程中,下列说法正确的是( )
A.挡板AO的弹力逐渐增大 B.挡板AO的弹力先增大后减小
C.挡板BO的弹力逐渐增减小 D.挡板BO的弹力先增大后减小
3.一质量为m的木块能够静止于倾角的斜面上,现对木块施加恒定的水平力,木块仍静止在斜面上,如图所示.则木块在前、后两种情况下所受的摩擦力大小之比为( )
A. B. C. D.
4.如图所示为一个东南亚风格的吊灯,吊灯由八根相同长度的轻绳吊于天花板挂钩上,每根轻绳与竖直方向的夹角为45°,吊灯质量为20kg,重力加速度为10m/s2。每根绳拉力大小是( )
A.20N B.20N
C.25N D.25N
5.如图所示,蛋糕和包装盒的总质量为m,包装盒为一长方体,上表面是边长为L的正方形,包装带与上表面的接触点均为各边的中点。现用手拉住包装带的交叉点,提起蛋糕使其静止不动,此时每一条倾斜的包装带长度都是。设蛋糕和包装盒质量分布均匀,包装带质量不计,已知重力加速度为g,则每条倾斜包装带的张力为( )
A. B.
C. D.
6.如图所示,A、B两木块放在粗糙水平面上,它们之间用不可伸长的轻绳相连,两次连接情况中轻绳倾斜方向不同,已知两木块与水平面间的动摩擦因数分别为μA和μB,且0<μA<μB,先后用水平拉力F1和F2拉着A、B一起水平向右匀速运动,则匀速运动过程中( )
A.F1B.F1>F2
C.F1=F2
D.无法确定
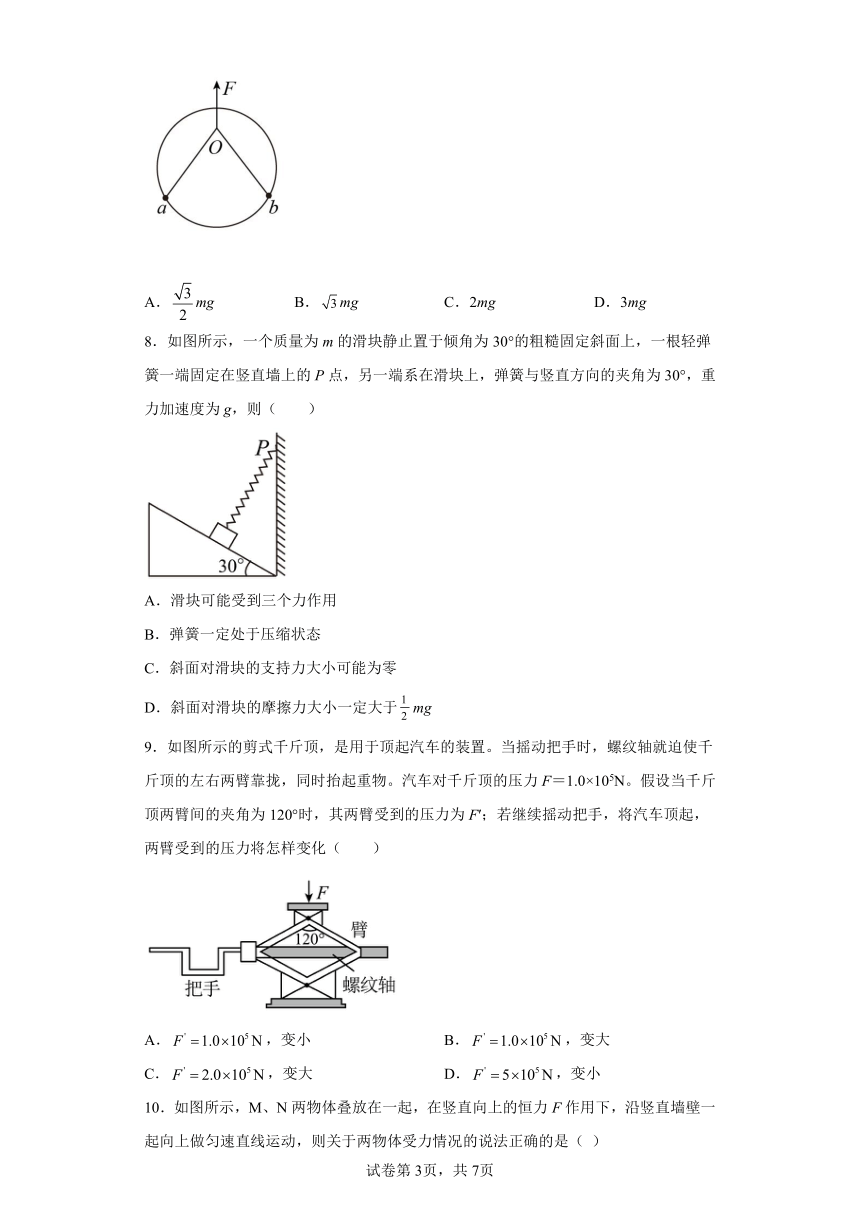
7.如图所示,两个质量均为m的小球a和b套在竖直固定的光滑圆环上,圆环半径为R,一不可伸长的细线两端各系在一个小球上,细线长为2R。用竖直向上的力F拉细线中点O,可使两小球保持等高静止在圆上不同高度处。当a、b间的距离为R时,力F的大小为(重力加速度为g)( )
A.mg B.mg C.2mg D.3mg
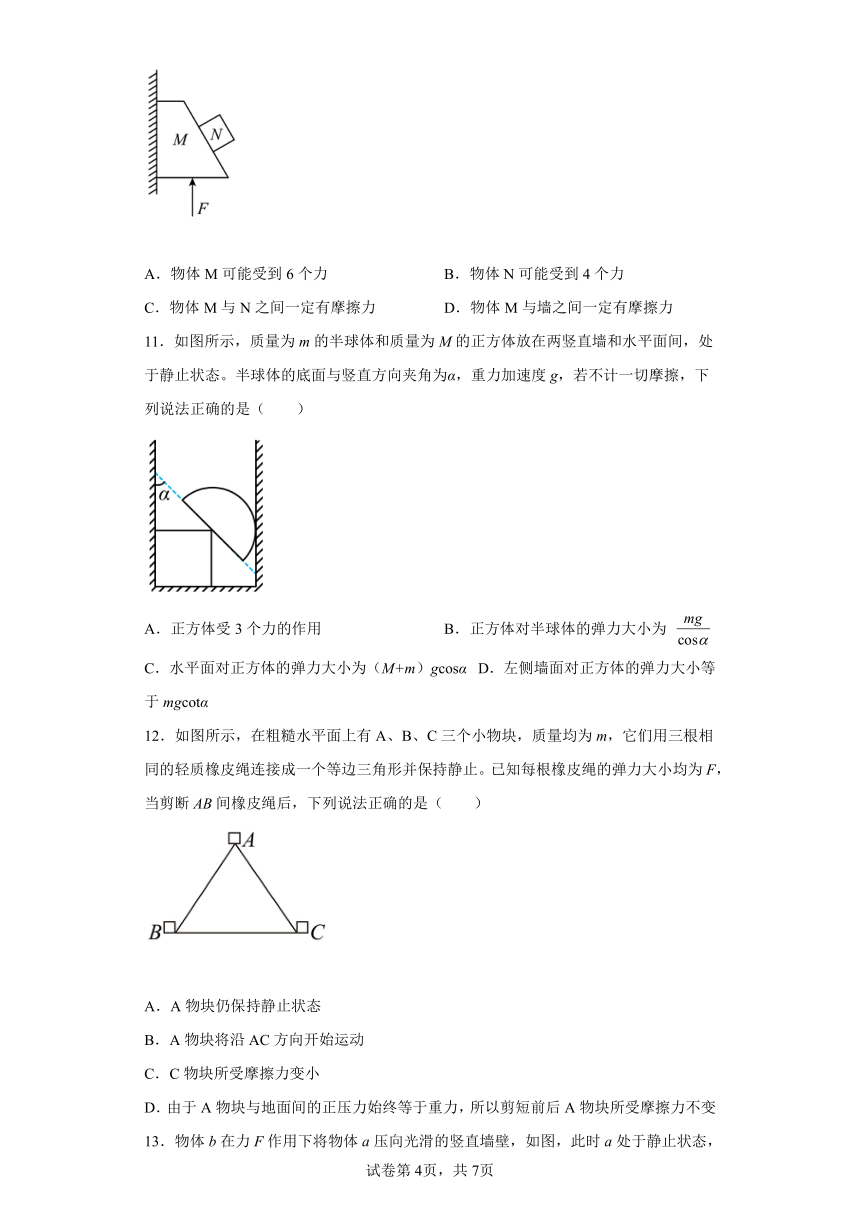
8.如图所示,一个质量为m的滑块静止置于倾角为30°的粗糙固定斜面上,一根轻弹簧一端固定在竖直墙上的P点,另一端系在滑块上,弹簧与竖直方向的夹角为30°,重力加速度为g,则( )
A.滑块可能受到三个力作用
B.弹簧一定处于压缩状态
C.斜面对滑块的支持力大小可能为零
D.斜面对滑块的摩擦力大小一定大于mg
9.如图所示的剪式千斤顶,是用于顶起汽车的装置。当摇动把手时,螺纹轴就迫使千斤顶的左右两臂靠拢,同时抬起重物。汽车对千斤顶的压力F=1.0×105N。假设当千斤顶两臂间的夹角为120°时,其两臂受到的压力为F′;若继续摇动把手,将汽车顶起,两臂受到的压力将怎样变化( )
A.,变小 B.,变大
C.,变大 D.,变小
10.如图所示,M、N两物体叠放在一起,在竖直向上的恒力F作用下,沿竖直墙壁一起向上做匀速直线运动,则关于两物体受力情况的说法正确的是( )
A.物体M可能受到6个力 B.物体N可能受到4个力
C.物体M与N之间一定有摩擦力 D.物体M与墙之间一定有摩擦力
11.如图所示,质量为m的半球体和质量为M的正方体放在两竖直墙和水平面间,处于静止状态。半球体的底面与竖直方向夹角为α,重力加速度g,若不计一切摩擦,下列说法正确的是( )
A.正方体受3个力的作用 B.正方体对半球体的弹力大小为
C.水平面对正方体的弹力大小为(M+m)gcosα D.左侧墙面对正方体的弹力大小等于mgcotα
12.如图所示,在粗糙水平面上有A、B、C三个小物块,质量均为m,它们用三根相同的轻质橡皮绳连接成一个等边三角形并保持静止。已知每根橡皮绳的弹力大小均为F,当剪断AB间橡皮绳后,下列说法正确的是( )
A.A物块仍保持静止状态
B.A物块将沿AC方向开始运动
C.C物块所受摩擦力变小
D.由于A物块与地面间的正压力始终等于重力,所以剪短前后A物块所受摩擦力不变
13.物体b在力F作用下将物体a压向光滑的竖直墙壁,如图,此时a处于静止状态,下列说法正确的是( )
A.F增大时,a受的摩擦力大小不变
B.F增大时,a受的摩擦力增大
C.F减小时,a仍然会处于静止状态
D.a受的摩擦力方向始终竖直向下
14.如图,一重力不计的梯子斜靠在光滑竖直墙壁上,重为G的工人由地面沿梯子上爬,在上爬过程中,梯子保持静止 设墙壁对梯子的作用力为F1,地面对梯子的支持力为F2,摩擦力为F3,则在上爬过程中( )
A.F1由大变小 B.F2由大变小 C.F2由小变大 D.F3由小变大
15.如图所示,A、B为竖直墙面上等高的两点,AO、BO为长度相等的两根轻绳,AOB在同一水平面内,初始时∠AOB<90°,CO为一根轻杆,可绕C点在空间无摩擦转动,转轴C在AB中点D的正下方,在O点处悬挂一个质量为m的物体,整个系统处于平衡状态,现将绳AO的A端缓缓向D端移动,O点位置保持不动,系统仍然保持平衡,则( )
A.绳AO的拉力逐渐增大
B.绳BO的拉力逐渐增大
C.杆CO受到的压力逐渐增大
D.绳AO、BO的拉力的合力逐渐增大
二、填空题
16.质量为的光滑球被竖直挡板挡住,静止在倾角为的斜面上,如图所示,则小球压紧挡板的力的大小________.
17.如果三个共点力的合力为零,那么任意两个力的合力大小一定______,方向与______。
18.如图所示,小球用细绳系住,绳的另一端固定于O点,现用水平F缓慢推动斜面体,小球在斜面上无摩擦地滑动,细绳始终处于绷紧状态,当小球升到接近斜面顶端时细绳接近水平,此过程中小球受重力、拉力和支持力作用,其中大小和方向都不变的力是______,方向不变、大小改变的力是______,大小和方向都发生变化的是______,拉力大小______(选填:“变大”、“变小”、“先变大后变小”或“先变小后变大”)。
三、解答题
19.如图所示,某人用轻绳牵住一质量的氢气球站立在地面上,因受水平风力的作用,系气球的轻绳与水平方向成37°角。已知空气对气球的浮力,方向竖直向上,人的质量,人受的浮力和风力忽略不计。(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
(1)水平风力F和轻绳拉力T的大小;
(2)地面对人的支持力和摩擦力f的大小。
20.如图所示,三根细轻绳系于O点,其中OA绳另一端固定于A点,OB绳的另一端与放在水平地面上质量m2为20kg的物体乙相连,OC绳的另一端悬挂质量m1为8kg的钩码甲。平衡时轻绳OA与竖直方向的夹角θ=37,OB绳水平。已知 重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,tan37°=0.75。
(1)求轻绳OA受到的拉力FOA大小,OB受到的拉力FOB大小;
(2)求乙受到的摩擦力;
(3)已知物体乙与水平桌面间的最大静摩擦力fmax为120N,若在钩码下方继续加挂钩码,为使物体在原位置保持静止,求最多能再加挂的钩码质量。
21.如图所示,轻杆BC的C点用光滑铰链与墙壁固定,杆的点通过水平轻质细绳AB使杆与竖直墙壁保持的夹角。若在点悬挂一个光滑定滑轮(不计重力),某人通过绕绳用它匀速地提起重物。已知重物的质量,绕绳质量不计,人的质量,取,,。试求:
(1)此时地面对人的支持力的大小;
(2)轻杆所受力的大小。
22.如图所示,在倾角为θ的粗糙斜面上,有一个质量为m的物体被水平力F推着静止于斜面上,物体与斜面间的动摩擦因数为μ,且μ<tanθ,求:
(1)力F多大时,物体不受摩擦力;
(2)为使物体静止在斜面上,力F的取值范围。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【详解】
设物体沿水平面做匀速直线运动时拉力大小为F,拉力方向与水平方向夹角为,水平面对物体的支持力大小为,对物体进行受力分析如图所示
由平衡条件有
联立解得
由几何知识可知,当
时,F有最小值
故选B。
2.B
【详解】
AB.V型光滑挡板转动过程中,对小球受力分析,各个力的夹角如图所示
由拉密定理可得
因为整个装置以O点为轴顺时针缓慢转动(∠AOB保持不变),故保持不变,在AO由水平转动90°到竖直的过程中,从锐角增大到钝角,先增大后减小,故挡板AO的弹力先增大后减小,A错误,B正确;
CD.从180°减小到90°,一直增大,故挡板BO的弹力一直增大,CD错误。
故选B。
3.C
【详解】
没有F作用时木块静止在斜面上时,由平衡条件知
F作用后木块仍静止,在斜面平面内,F与重力下滑分力的合力与静摩擦力平衡,则有
带入题中数据可得
故选C。
4.D
【详解】
设每根绳拉力大小为F,将各绳拉力正交分解到水平面上和竖直向上方向上,则竖直方向有
代入数据得
故D正确。
5.C
【详解】
设每条包装带与竖直方向夹角为,由几何关系得
所以
则由平衡条件得
解得每条倾斜包装带的张力为
故选C。
6.B
【详解】
对上图情形,分析受力情况,根据平衡条件得
F=fA+fB
fA=μA(mAg-T1sinθ)
fB=μB(mBg+T1sinθ)
联立得到
F1=μA(mAg-T1sinθ)+μB(mBg+T1sinθ)=μAmAg+μBmBg+(μB-μA)T1sinθ
同理,对下图情形,得到
F2=μA(mAg+T2sin )+μB(mBg-T2sin )=μAmAg+μBmBg-(μB-μA)T2sin
因为0<μA<μB,可知
F1>F2
故选B。
7.D
【详解】
a、b等高且距离为R,O为细线中点且细线长为2R,则
三角形为等边三角形,如图
选取左侧小球进行分析,记为圆心,由图中几何关系可得,圆环弹力沿向外,与水平方向夹角为,则小球所受重力与圆环弹力的合外力为
与绳拉力T等大,力F的大小与绳拉力的合力等大反向,三角形为等边三角形,两绳夹角为,故
ABC错误,D正确。
故选D。
8.A
【详解】
AB.假设没有弹簧且斜面足够粗糙,滑块也可能静止在题图所示位置,所以弹簧可能处于原长状态,此时滑块受到三个力的作用,故A正确,B错误;
C.如果斜面对滑块的支持力大小为零,那么斜面与滑块之间肯定没有摩擦力,滑块只受到竖直向下的重力和沿弹簧方向的力,不可能平衡,所以斜面对滑块的支持力大小不可能为零,故C错误;
D.根据滑块沿斜面方向上二力平衡可知,斜面对滑块的摩擦力大小一定等于
故D错误。
故选A。
9.A
【详解】
如图所示
将汽车对千斤顶的压力F沿两臂分解为F1、F2,根据对称性可知,两臂受到的压力大小相等,即
F1=F2=F′
由
2F′cosθ=F
可得
F′==1.0×105N
继续摇动把手,两臂靠拢,夹角减小,由
F′=
分析可知,F不变,当θ减小时,cosθ增大,F′减小,BCD错误,A正确。
故选A。
10.C
【详解】
BC.对N进行受力分析如图所示
可知N一定受重力mg,M对N的弹力FN,M对N的摩擦力f,3个力的作用,才能处于平衡状态,B错误,C正确;
AD.将M、N作为一个整体,可知墙壁对M一定不存在弹力,否则不可能平衡,由于弹力是摩擦力的前提,因此墙壁与M之间一定没有摩擦力,因此M一定受到4个力的作用,AD错误。
故选C。
11.D
【详解】
A.对正方体进行受力分析,受到重力、地面的支持力、半球体对它的压力以及左侧墙壁对它的支持力,所以正方体受到4个力作用,故A错误;
B.对半球体进行受力分析,受到重力、正方体的弹力和右侧墙壁对它的支持力,如图所示,把正方体对半球体的弹力FN2沿水平方向和竖直方向分解,可得
FN2sinα=mg
解得
FN2=
故B错误;
C.以两个物体所组成的系统为研究对象,竖直方向上系统受到向上的支持力和向下的重力,整体处于静止状态,所以水平面对正方体的弹力大小为(M+m)g,故C错误;
D.墙面对半球体的弹力大小
FN1=FN2cosα
解得
FN1=mgcotα
以整体为研究对象,水平方向上系统受到左右两侧墙面的弹力而平衡,所以左侧墙面对正方体的弹力大小等于mgcotα,故D正确。
故选D。
12.A
【详解】
C.对于C,剪断AB间橡皮绳时,AC,BC间弹性绳形变未发生变化,则弹力仍为F,则C仍静止,摩擦力不变,C错误;
ABD.对于A,剪断前,A受到的AC、AB绳子拉力的合力
剪断AB间橡皮绳时,AB绳子弹力为零,AC间弹性绳形变未发生变化,A受到拉力为F,小于,则A仍静止,根据平衡,剪断后A的摩擦力变小,BD错误A正确。
故选A。
13.A
【详解】
ABD.a处于静止状态时,对于a受力分析,由于墙壁光滑,受到重力、b对a的压力、墙壁的弹力、b对a的摩擦力,则b对a的摩擦力大小等于a的重力,方向竖直向上;F增大,摩擦力大小不变,始终等于a的重力。故A正确,BD错误;
C. F减小时,b对a的压力减小,a、b间的最大静摩擦力减小,当最大静摩擦力小于a的重力时,a会下滑,故C错误。
故选A。
14.D
【详解】
A.对梯子和人整体受力分析,如图所示
在人上爬的过程中,力的作用线的交点水平向左移动,F和竖直方向的夹角变大,有几何关系可知
即F1由小变大,A错误;
BC.
即F2保持不变,B错误,C错误;
D.
即F3由小变大,D正确;
故选D。
15.A
【详解】
CD.设绳AO和绳BO拉力的合力为F,以O点为研究对象,O点受到重力mg、杆的支持力F2和绳AO与绳BO拉力的合力F,作出力的示意图如图所示
当重力不变、杆与竖直方向的夹角不变时,杆的支持力F2不变,绳AO与绳BO拉力的合力F也不变,仍沿OD方向,故CD错误;
AB.当A点逐渐靠近D点时,将绳AO和绳BO的拉力合成如图所示
可知绳AO的拉力逐渐增大,绳BO的拉力逐渐减小,故A正确,B错误。
故选A。
16.
【详解】
受力分析如图所示,由平衡条件可得挡板对小球的作用力
由牛顿第三定律可知,小球压紧挡板的力的大小为。
17. 与第三个力的大小相等 第三个力的方向相反
【详解】
[1][2]如果三个共点力的合力为零,那么任意两个力的合力大小一定与第三个力的大小相等,方向与第三个力的方向相反。把两个等效为一个力,则三力平衡等效为二力平衡。
18. 重力 支持力 拉力 先变小后变大
【详解】
[1][2][3]此过程中小球受重力、拉力和支持力作用,其中大小和方向都不变的力是重力;方向不变、大小改变的力是支持力;大小和方向都发生变化的是拉力;
[4]重力、斜面对小球的支持力FN、绳子拉力FT组成一个闭合的矢量三角形,如图所示:
由于重力不变、支持力FN方向不变,且从已知图形知开始时β>θ,斜面向左移动的过程中,拉力FT与水平方向的夹角β逐渐变小,逐渐趋向于0;当β=θ时,拉力与斜面平行,此时细绳的拉力FT最小,由图可知,随β的减小, FT先减小后增大;
19.(1)20N,25N;(2)485N,20N
【详解】
(1)对气球根据平衡条件有
解得
(2)对人根据平衡条件有
20.(1)100N,60N;(2)60N,水平向左;(3)8kg
【详解】
(1)对结点O受力分析,将甲对结点的拉力分解如图
由几何关系有
(2)乙物体在水平方向受力平衡,根据平衡条件可得,乙受到的摩擦力为
f=FOB=60N
水平向左;
(3)考虑物体乙恰好不滑动的临界情况,则根据平衡条件可得
故可得
21.(1)300N;(2)500N
【详解】
(1)因人匀速提起重物,则绕绳上的拉力与重物的重力相等,即
对人受力分析,由平衡条件可得
代入数据,解得地面对人的支持力的大小为
FN=300N
(2)对B点受力分析,由平衡条件可得
=N=500N
由牛顿第三定律可知,轻杆BC所受力大小为500N。
22.(1);(2)
【详解】
(1)物体不受摩擦力时受力如图1所示
由平衡条件得
解得
(2)当物体恰不沿斜面向下滑动时,F最小,物体受力如图2所示
由平衡条件得:沿斜面方向
垂直斜面方向
又
解得
当物体恰不沿斜面向上滑动时,F最大,物体受力如图3所示
由平衡条件得:沿斜面方向
垂直斜面方向
又
解得
为使物体静止在斜面上,力F的取值范围是
答案第1页,共2页
答案第1页,共2页
一、单选题
1.日常生活、生产中,常常需要将物体水平移动。一重量为G的物体与水平面间动摩擦因数为0.75,最大静摩擦力等于滑动摩擦力,不计空气阻力,则要使该物体沿该水平面做匀速直线运动的最小拉力为( )
A.0.75G B.0.6G C.0.5G D.0.3G
2.如图所示,V型光滑挡板AOB之间放置有一质量均匀的球体,初始时系统处于静止状态,现将整个装置以O点为轴顺时针缓慢转动(∠AOB保持不变),在AO由水平转动90°到竖直的过程中,下列说法正确的是( )
A.挡板AO的弹力逐渐增大 B.挡板AO的弹力先增大后减小
C.挡板BO的弹力逐渐增减小 D.挡板BO的弹力先增大后减小
3.一质量为m的木块能够静止于倾角的斜面上,现对木块施加恒定的水平力,木块仍静止在斜面上,如图所示.则木块在前、后两种情况下所受的摩擦力大小之比为( )
A. B. C. D.
4.如图所示为一个东南亚风格的吊灯,吊灯由八根相同长度的轻绳吊于天花板挂钩上,每根轻绳与竖直方向的夹角为45°,吊灯质量为20kg,重力加速度为10m/s2。每根绳拉力大小是( )
A.20N B.20N
C.25N D.25N
5.如图所示,蛋糕和包装盒的总质量为m,包装盒为一长方体,上表面是边长为L的正方形,包装带与上表面的接触点均为各边的中点。现用手拉住包装带的交叉点,提起蛋糕使其静止不动,此时每一条倾斜的包装带长度都是。设蛋糕和包装盒质量分布均匀,包装带质量不计,已知重力加速度为g,则每条倾斜包装带的张力为( )
A. B.
C. D.
6.如图所示,A、B两木块放在粗糙水平面上,它们之间用不可伸长的轻绳相连,两次连接情况中轻绳倾斜方向不同,已知两木块与水平面间的动摩擦因数分别为μA和μB,且0<μA<μB,先后用水平拉力F1和F2拉着A、B一起水平向右匀速运动,则匀速运动过程中( )
A.F1
C.F1=F2
D.无法确定
7.如图所示,两个质量均为m的小球a和b套在竖直固定的光滑圆环上,圆环半径为R,一不可伸长的细线两端各系在一个小球上,细线长为2R。用竖直向上的力F拉细线中点O,可使两小球保持等高静止在圆上不同高度处。当a、b间的距离为R时,力F的大小为(重力加速度为g)( )
A.mg B.mg C.2mg D.3mg
8.如图所示,一个质量为m的滑块静止置于倾角为30°的粗糙固定斜面上,一根轻弹簧一端固定在竖直墙上的P点,另一端系在滑块上,弹簧与竖直方向的夹角为30°,重力加速度为g,则( )
A.滑块可能受到三个力作用
B.弹簧一定处于压缩状态
C.斜面对滑块的支持力大小可能为零
D.斜面对滑块的摩擦力大小一定大于mg
9.如图所示的剪式千斤顶,是用于顶起汽车的装置。当摇动把手时,螺纹轴就迫使千斤顶的左右两臂靠拢,同时抬起重物。汽车对千斤顶的压力F=1.0×105N。假设当千斤顶两臂间的夹角为120°时,其两臂受到的压力为F′;若继续摇动把手,将汽车顶起,两臂受到的压力将怎样变化( )
A.,变小 B.,变大
C.,变大 D.,变小
10.如图所示,M、N两物体叠放在一起,在竖直向上的恒力F作用下,沿竖直墙壁一起向上做匀速直线运动,则关于两物体受力情况的说法正确的是( )
A.物体M可能受到6个力 B.物体N可能受到4个力
C.物体M与N之间一定有摩擦力 D.物体M与墙之间一定有摩擦力
11.如图所示,质量为m的半球体和质量为M的正方体放在两竖直墙和水平面间,处于静止状态。半球体的底面与竖直方向夹角为α,重力加速度g,若不计一切摩擦,下列说法正确的是( )
A.正方体受3个力的作用 B.正方体对半球体的弹力大小为
C.水平面对正方体的弹力大小为(M+m)gcosα D.左侧墙面对正方体的弹力大小等于mgcotα
12.如图所示,在粗糙水平面上有A、B、C三个小物块,质量均为m,它们用三根相同的轻质橡皮绳连接成一个等边三角形并保持静止。已知每根橡皮绳的弹力大小均为F,当剪断AB间橡皮绳后,下列说法正确的是( )
A.A物块仍保持静止状态
B.A物块将沿AC方向开始运动
C.C物块所受摩擦力变小
D.由于A物块与地面间的正压力始终等于重力,所以剪短前后A物块所受摩擦力不变
13.物体b在力F作用下将物体a压向光滑的竖直墙壁,如图,此时a处于静止状态,下列说法正确的是( )
A.F增大时,a受的摩擦力大小不变
B.F增大时,a受的摩擦力增大
C.F减小时,a仍然会处于静止状态
D.a受的摩擦力方向始终竖直向下
14.如图,一重力不计的梯子斜靠在光滑竖直墙壁上,重为G的工人由地面沿梯子上爬,在上爬过程中,梯子保持静止 设墙壁对梯子的作用力为F1,地面对梯子的支持力为F2,摩擦力为F3,则在上爬过程中( )
A.F1由大变小 B.F2由大变小 C.F2由小变大 D.F3由小变大
15.如图所示,A、B为竖直墙面上等高的两点,AO、BO为长度相等的两根轻绳,AOB在同一水平面内,初始时∠AOB<90°,CO为一根轻杆,可绕C点在空间无摩擦转动,转轴C在AB中点D的正下方,在O点处悬挂一个质量为m的物体,整个系统处于平衡状态,现将绳AO的A端缓缓向D端移动,O点位置保持不动,系统仍然保持平衡,则( )
A.绳AO的拉力逐渐增大
B.绳BO的拉力逐渐增大
C.杆CO受到的压力逐渐增大
D.绳AO、BO的拉力的合力逐渐增大
二、填空题
16.质量为的光滑球被竖直挡板挡住,静止在倾角为的斜面上,如图所示,则小球压紧挡板的力的大小________.
17.如果三个共点力的合力为零,那么任意两个力的合力大小一定______,方向与______。
18.如图所示,小球用细绳系住,绳的另一端固定于O点,现用水平F缓慢推动斜面体,小球在斜面上无摩擦地滑动,细绳始终处于绷紧状态,当小球升到接近斜面顶端时细绳接近水平,此过程中小球受重力、拉力和支持力作用,其中大小和方向都不变的力是______,方向不变、大小改变的力是______,大小和方向都发生变化的是______,拉力大小______(选填:“变大”、“变小”、“先变大后变小”或“先变小后变大”)。
三、解答题
19.如图所示,某人用轻绳牵住一质量的氢气球站立在地面上,因受水平风力的作用,系气球的轻绳与水平方向成37°角。已知空气对气球的浮力,方向竖直向上,人的质量,人受的浮力和风力忽略不计。(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
(1)水平风力F和轻绳拉力T的大小;
(2)地面对人的支持力和摩擦力f的大小。
20.如图所示,三根细轻绳系于O点,其中OA绳另一端固定于A点,OB绳的另一端与放在水平地面上质量m2为20kg的物体乙相连,OC绳的另一端悬挂质量m1为8kg的钩码甲。平衡时轻绳OA与竖直方向的夹角θ=37,OB绳水平。已知 重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,tan37°=0.75。
(1)求轻绳OA受到的拉力FOA大小,OB受到的拉力FOB大小;
(2)求乙受到的摩擦力;
(3)已知物体乙与水平桌面间的最大静摩擦力fmax为120N,若在钩码下方继续加挂钩码,为使物体在原位置保持静止,求最多能再加挂的钩码质量。
21.如图所示,轻杆BC的C点用光滑铰链与墙壁固定,杆的点通过水平轻质细绳AB使杆与竖直墙壁保持的夹角。若在点悬挂一个光滑定滑轮(不计重力),某人通过绕绳用它匀速地提起重物。已知重物的质量,绕绳质量不计,人的质量,取,,。试求:
(1)此时地面对人的支持力的大小;
(2)轻杆所受力的大小。
22.如图所示,在倾角为θ的粗糙斜面上,有一个质量为m的物体被水平力F推着静止于斜面上,物体与斜面间的动摩擦因数为μ,且μ<tanθ,求:
(1)力F多大时,物体不受摩擦力;
(2)为使物体静止在斜面上,力F的取值范围。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【详解】
设物体沿水平面做匀速直线运动时拉力大小为F,拉力方向与水平方向夹角为,水平面对物体的支持力大小为,对物体进行受力分析如图所示
由平衡条件有
联立解得
由几何知识可知,当
时,F有最小值
故选B。
2.B
【详解】
AB.V型光滑挡板转动过程中,对小球受力分析,各个力的夹角如图所示
由拉密定理可得
因为整个装置以O点为轴顺时针缓慢转动(∠AOB保持不变),故保持不变,在AO由水平转动90°到竖直的过程中,从锐角增大到钝角,先增大后减小,故挡板AO的弹力先增大后减小,A错误,B正确;
CD.从180°减小到90°,一直增大,故挡板BO的弹力一直增大,CD错误。
故选B。
3.C
【详解】
没有F作用时木块静止在斜面上时,由平衡条件知
F作用后木块仍静止,在斜面平面内,F与重力下滑分力的合力与静摩擦力平衡,则有
带入题中数据可得
故选C。
4.D
【详解】
设每根绳拉力大小为F,将各绳拉力正交分解到水平面上和竖直向上方向上,则竖直方向有
代入数据得
故D正确。
5.C
【详解】
设每条包装带与竖直方向夹角为,由几何关系得
所以
则由平衡条件得
解得每条倾斜包装带的张力为
故选C。
6.B
【详解】
对上图情形,分析受力情况,根据平衡条件得
F=fA+fB
fA=μA(mAg-T1sinθ)
fB=μB(mBg+T1sinθ)
联立得到
F1=μA(mAg-T1sinθ)+μB(mBg+T1sinθ)=μAmAg+μBmBg+(μB-μA)T1sinθ
同理,对下图情形,得到
F2=μA(mAg+T2sin )+μB(mBg-T2sin )=μAmAg+μBmBg-(μB-μA)T2sin
因为0<μA<μB,可知
F1>F2
故选B。
7.D
【详解】
a、b等高且距离为R,O为细线中点且细线长为2R,则
三角形为等边三角形,如图
选取左侧小球进行分析,记为圆心,由图中几何关系可得,圆环弹力沿向外,与水平方向夹角为,则小球所受重力与圆环弹力的合外力为
与绳拉力T等大,力F的大小与绳拉力的合力等大反向,三角形为等边三角形,两绳夹角为,故
ABC错误,D正确。
故选D。
8.A
【详解】
AB.假设没有弹簧且斜面足够粗糙,滑块也可能静止在题图所示位置,所以弹簧可能处于原长状态,此时滑块受到三个力的作用,故A正确,B错误;
C.如果斜面对滑块的支持力大小为零,那么斜面与滑块之间肯定没有摩擦力,滑块只受到竖直向下的重力和沿弹簧方向的力,不可能平衡,所以斜面对滑块的支持力大小不可能为零,故C错误;
D.根据滑块沿斜面方向上二力平衡可知,斜面对滑块的摩擦力大小一定等于
故D错误。
故选A。
9.A
【详解】
如图所示
将汽车对千斤顶的压力F沿两臂分解为F1、F2,根据对称性可知,两臂受到的压力大小相等,即
F1=F2=F′
由
2F′cosθ=F
可得
F′==1.0×105N
继续摇动把手,两臂靠拢,夹角减小,由
F′=
分析可知,F不变,当θ减小时,cosθ增大,F′减小,BCD错误,A正确。
故选A。
10.C
【详解】
BC.对N进行受力分析如图所示
可知N一定受重力mg,M对N的弹力FN,M对N的摩擦力f,3个力的作用,才能处于平衡状态,B错误,C正确;
AD.将M、N作为一个整体,可知墙壁对M一定不存在弹力,否则不可能平衡,由于弹力是摩擦力的前提,因此墙壁与M之间一定没有摩擦力,因此M一定受到4个力的作用,AD错误。
故选C。
11.D
【详解】
A.对正方体进行受力分析,受到重力、地面的支持力、半球体对它的压力以及左侧墙壁对它的支持力,所以正方体受到4个力作用,故A错误;
B.对半球体进行受力分析,受到重力、正方体的弹力和右侧墙壁对它的支持力,如图所示,把正方体对半球体的弹力FN2沿水平方向和竖直方向分解,可得
FN2sinα=mg
解得
FN2=
故B错误;
C.以两个物体所组成的系统为研究对象,竖直方向上系统受到向上的支持力和向下的重力,整体处于静止状态,所以水平面对正方体的弹力大小为(M+m)g,故C错误;
D.墙面对半球体的弹力大小
FN1=FN2cosα
解得
FN1=mgcotα
以整体为研究对象,水平方向上系统受到左右两侧墙面的弹力而平衡,所以左侧墙面对正方体的弹力大小等于mgcotα,故D正确。
故选D。
12.A
【详解】
C.对于C,剪断AB间橡皮绳时,AC,BC间弹性绳形变未发生变化,则弹力仍为F,则C仍静止,摩擦力不变,C错误;
ABD.对于A,剪断前,A受到的AC、AB绳子拉力的合力
剪断AB间橡皮绳时,AB绳子弹力为零,AC间弹性绳形变未发生变化,A受到拉力为F,小于,则A仍静止,根据平衡,剪断后A的摩擦力变小,BD错误A正确。
故选A。
13.A
【详解】
ABD.a处于静止状态时,对于a受力分析,由于墙壁光滑,受到重力、b对a的压力、墙壁的弹力、b对a的摩擦力,则b对a的摩擦力大小等于a的重力,方向竖直向上;F增大,摩擦力大小不变,始终等于a的重力。故A正确,BD错误;
C. F减小时,b对a的压力减小,a、b间的最大静摩擦力减小,当最大静摩擦力小于a的重力时,a会下滑,故C错误。
故选A。
14.D
【详解】
A.对梯子和人整体受力分析,如图所示
在人上爬的过程中,力的作用线的交点水平向左移动,F和竖直方向的夹角变大,有几何关系可知
即F1由小变大,A错误;
BC.
即F2保持不变,B错误,C错误;
D.
即F3由小变大,D正确;
故选D。
15.A
【详解】
CD.设绳AO和绳BO拉力的合力为F,以O点为研究对象,O点受到重力mg、杆的支持力F2和绳AO与绳BO拉力的合力F,作出力的示意图如图所示
当重力不变、杆与竖直方向的夹角不变时,杆的支持力F2不变,绳AO与绳BO拉力的合力F也不变,仍沿OD方向,故CD错误;
AB.当A点逐渐靠近D点时,将绳AO和绳BO的拉力合成如图所示
可知绳AO的拉力逐渐增大,绳BO的拉力逐渐减小,故A正确,B错误。
故选A。
16.
【详解】
受力分析如图所示,由平衡条件可得挡板对小球的作用力
由牛顿第三定律可知,小球压紧挡板的力的大小为。
17. 与第三个力的大小相等 第三个力的方向相反
【详解】
[1][2]如果三个共点力的合力为零,那么任意两个力的合力大小一定与第三个力的大小相等,方向与第三个力的方向相反。把两个等效为一个力,则三力平衡等效为二力平衡。
18. 重力 支持力 拉力 先变小后变大
【详解】
[1][2][3]此过程中小球受重力、拉力和支持力作用,其中大小和方向都不变的力是重力;方向不变、大小改变的力是支持力;大小和方向都发生变化的是拉力;
[4]重力、斜面对小球的支持力FN、绳子拉力FT组成一个闭合的矢量三角形,如图所示:
由于重力不变、支持力FN方向不变,且从已知图形知开始时β>θ,斜面向左移动的过程中,拉力FT与水平方向的夹角β逐渐变小,逐渐趋向于0;当β=θ时,拉力与斜面平行,此时细绳的拉力FT最小,由图可知,随β的减小, FT先减小后增大;
19.(1)20N,25N;(2)485N,20N
【详解】
(1)对气球根据平衡条件有
解得
(2)对人根据平衡条件有
20.(1)100N,60N;(2)60N,水平向左;(3)8kg
【详解】
(1)对结点O受力分析,将甲对结点的拉力分解如图
由几何关系有
(2)乙物体在水平方向受力平衡,根据平衡条件可得,乙受到的摩擦力为
f=FOB=60N
水平向左;
(3)考虑物体乙恰好不滑动的临界情况,则根据平衡条件可得
故可得
21.(1)300N;(2)500N
【详解】
(1)因人匀速提起重物,则绕绳上的拉力与重物的重力相等,即
对人受力分析,由平衡条件可得
代入数据,解得地面对人的支持力的大小为
FN=300N
(2)对B点受力分析,由平衡条件可得
=N=500N
由牛顿第三定律可知,轻杆BC所受力大小为500N。
22.(1);(2)
【详解】
(1)物体不受摩擦力时受力如图1所示
由平衡条件得
解得
(2)当物体恰不沿斜面向下滑动时,F最小,物体受力如图2所示
由平衡条件得:沿斜面方向
垂直斜面方向
又
解得
当物体恰不沿斜面向上滑动时,F最大,物体受力如图3所示
由平衡条件得:沿斜面方向
垂直斜面方向
又
解得
为使物体静止在斜面上,力F的取值范围是
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 绪论 撩开物理学的神秘面纱
- 一、源自然之问
- 二、探万物之秘
- 三、采科学之益
- 四、启智慧之迪
- 第1章 运动的描述
- 第1节 空间和时间
- 第2节 质点和位移
- 第3节 速度
- 第4节 加速度
- 第2章 匀变速直线运动
- 第1节 速度变化规律
- 第2节 位移变化规律
- 第3节 实验中的误差和有效数字
- 第4节 科学测量:做直线运动物体的瞬时速度
- 第5节 自由落体运动
- 第3章 相互作用
- 第1节 重力与重心
- 第2节 科学探究:弹力
- 第3节 摩擦力
- 第4章 力与平衡
- 第1节 科学探究:力的合成
- 第2节 力的分解
- 第3节 共点力的平衡
- 第5章 牛顿运动定律
- 第1节 牛顿第一运动定律
- 第2节 科学探究:加速度与力、质量的关系
- 第3节 牛顿第二运动定律
- 第4节 牛顿第三运动定律
- 第5节 超重与失重
