青岛版八年级数学下册 11.1 图形的平移 导学案 (无答案)
文档属性
| 名称 | 青岛版八年级数学下册 11.1 图形的平移 导学案 (无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 96.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-17 20:55:55 | ||
图片预览

文档简介
第11章图形的平移与旋转导学案(2)
学习内容: 11.1图形的平移(2)
学习目标:1、运用平移的概念和基本性质,按照要求画出简单平面图形后的图形,解决有关的实际问题。
2、通过方格中图案的平移解决计算问题。
学习重点:平移的概念和平移的性质.
学习难点:正确运用平移解数学问题。
学习过程:
【知识回顾】
什么是平移?决定平移的要素是什么?
图形的平移有哪些性质?
【自主学习】
一、自学教材P167---168页例2内容,仿照例2解法完成下列问题:
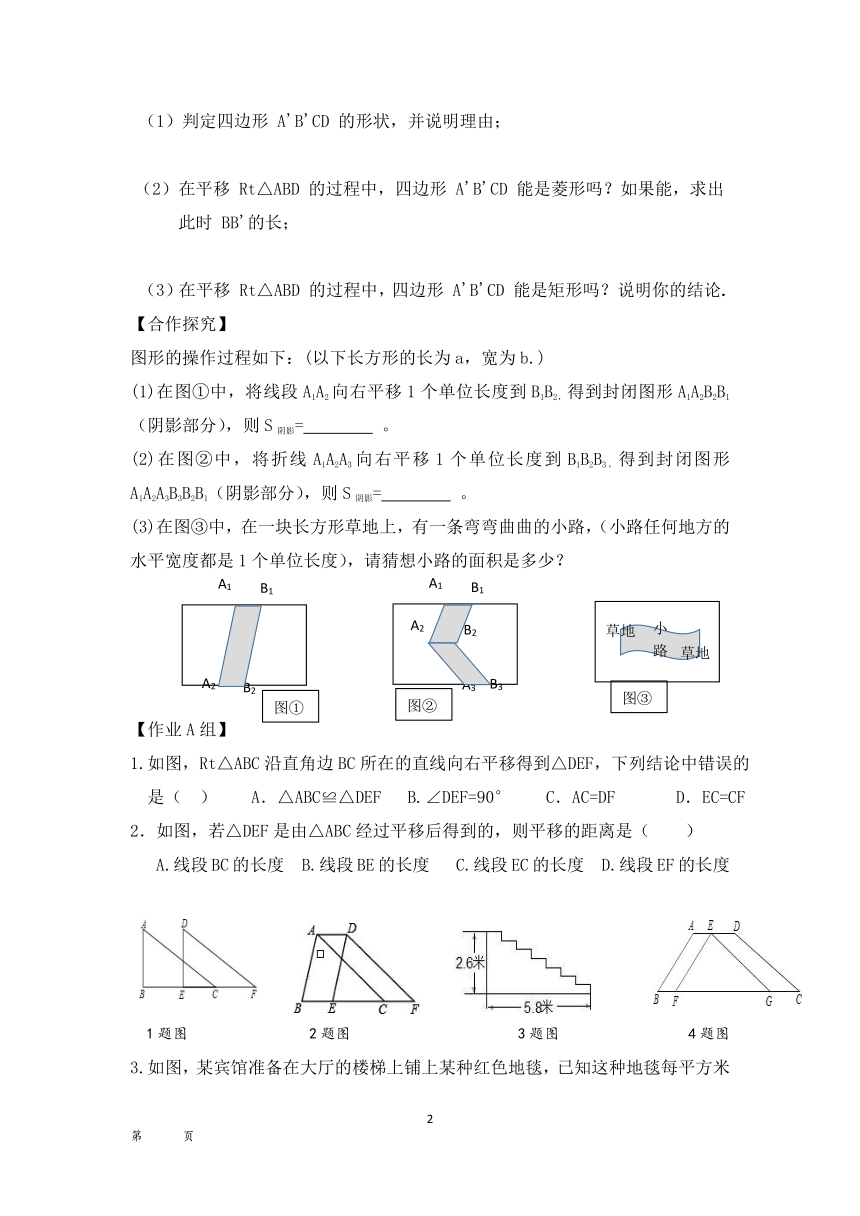
如图,在平行四边形ABCD中,CD=2.5cm
,垂足为E;交AB的延长
线于点F,△BCF可以看作是由
沿 方向平移 cm得到的。
当原平行四边形ABCD满足 时,平移后组成的四边形是正方形。
2.如图,把平行四边形ABCD中沿BD剪开,△ABD沿BD方向平移,平移的距离小于线段DB的长,画出平移后的图形。
(
D
C
B
A
)
二、自学教材P168---169页例3内容,仿照例2解法完成下列问题:
4、如图,将两只全等的含 30° 角的三角尺按图 ① 的方式摆放在一起得到矩形 ABCD . 固定 Rt△BCD,将 Rt△ABD 沿 BD 向右上方平移,得到图 ② 中的△A'B'D',连接 B'C,A'D.
(1)判定四边形 A'B'CD 的形状,并说明理由;
(2)在平移 Rt△ABD 的过程中,四边形 A'B'CD 能是菱形吗?如果能,求出此时 BB'的长;
(3)在平移 Rt△ABD 的过程中,四边形 A'B'CD 能是矩形吗?说明你的结论.
【合作探究】
图形的操作过程如下:(以下长方形的长为a,宽为b.)
(1)在图①中,将线段A1A2向右平移1个单位长度到B1B2,得到封闭图形A1A2B2B1(阴影部分),则S阴影= 。
(2)在图②中,将折线A1A2A3向右平移1个单位长度到B1B2B3,得到封闭图形A1A2A3B3B2B1(阴影部分),则S阴影= 。
(
B
2
B
1
A
2
A
1
B
3
B
1
A
3
A
1
A
2
B
2
草地
草地
小路
图
①
图
③
图
②
)(3)在图③中,在一块长方形草地上,有一条弯弯曲曲的小路,(小路任何地方的水平宽度都是1个单位长度),请猜想小路的面积是多少?
【作业A组】
1.如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论中错误的
是( ) A.△ABC≌△DEF B.∠DEF=90° C.AC=DF D.EC=CF
2.如图,若△DEF是由△ABC经过平移后得到的,则平移的距离是( )
A.线段BC的长度 B.线段BE的长度 C.线段EC的长度 D.线段EF的长度
1题图 2题图 3题图 4题图
3.如图,某宾馆准备在大厅的楼梯上铺上某种红色地毯,已知这种地毯每平方米售价30元,主楼梯道宽2米,其侧面如图所示,则购买地毯至少需要元 .
4. 如图所示,在四边形ABCD中,AD‖BC,BC>AD,∠B与∠C 互余,将AB,CD分别平移到EF和EG的位置,则△EFG为 三角形,若AD=2cm,BC=8cm,则FG= cm.
5. 如图,△BEF是由△ABC平移所得,点A,B,E在同一直 线上,若∠C=20°,∠ABC=68°,则∠CBF= 度
6.如图,已知△ABC的面积为16,BC=8.现将△ABC沿直线BC向右平移a个单位到△DEF的位置.
(1)当a=4时,求△ABC所扫过的面积;
(2)连接AE、AD,设AB=5,当DE=AD时,求a的值.
【作业B组】
1.将长度为3cm的线段向上平移20cm,所得线段的长度是( )
A.3cm B.23cm C.20cm D.17cm
2.如图,将△ABC沿BC方向平移2cm得到△DEF,若 △ABC的周长为16cm则四边形ABFD的周长为( ) A.16 cm B.18 cm C.20cm D.22cm
(
2
题图
3
题图
4
题图
)
3.如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当它移动的距离AA′等于4时,两个三角形重叠部分的面积为 .
4.如图,边长为4cm的正方形ABCD先向上平移2cm,再向右平移1cm,得到正方形A′B′C′D′,此时阴影部分的面积为 cm.
5.如图,边长为1的网格中有一个“柳叶”形图形,它是
由弧DG和弧EB和线段DE、GB围成的,两条弧的圆心
分别是点F和点A,半径都等于4,则“柳叶”形的面
积为 。
(
E
D
C
B
A
┘
)6、四边形ABCD中,AB‖CD,AC⊥BD,沿CD方向将线段BD平移到EC,平移的距离等于线段DC的长,连接BE。
(1)AC与CE是否垂直?为什么?
(2)△ACD与△BEC的面积是否相等?为什么?
(3)已知AC=a,BD=b,求梯形ABCD的面积。
(
4
) 第 页
学习内容: 11.1图形的平移(2)
学习目标:1、运用平移的概念和基本性质,按照要求画出简单平面图形后的图形,解决有关的实际问题。
2、通过方格中图案的平移解决计算问题。
学习重点:平移的概念和平移的性质.
学习难点:正确运用平移解数学问题。
学习过程:
【知识回顾】
什么是平移?决定平移的要素是什么?
图形的平移有哪些性质?
【自主学习】
一、自学教材P167---168页例2内容,仿照例2解法完成下列问题:
如图,在平行四边形ABCD中,CD=2.5cm
,垂足为E;交AB的延长
线于点F,△BCF可以看作是由
沿 方向平移 cm得到的。
当原平行四边形ABCD满足 时,平移后组成的四边形是正方形。
2.如图,把平行四边形ABCD中沿BD剪开,△ABD沿BD方向平移,平移的距离小于线段DB的长,画出平移后的图形。
(
D
C
B
A
)
二、自学教材P168---169页例3内容,仿照例2解法完成下列问题:
4、如图,将两只全等的含 30° 角的三角尺按图 ① 的方式摆放在一起得到矩形 ABCD . 固定 Rt△BCD,将 Rt△ABD 沿 BD 向右上方平移,得到图 ② 中的△A'B'D',连接 B'C,A'D.
(1)判定四边形 A'B'CD 的形状,并说明理由;
(2)在平移 Rt△ABD 的过程中,四边形 A'B'CD 能是菱形吗?如果能,求出此时 BB'的长;
(3)在平移 Rt△ABD 的过程中,四边形 A'B'CD 能是矩形吗?说明你的结论.
【合作探究】
图形的操作过程如下:(以下长方形的长为a,宽为b.)
(1)在图①中,将线段A1A2向右平移1个单位长度到B1B2,得到封闭图形A1A2B2B1(阴影部分),则S阴影= 。
(2)在图②中,将折线A1A2A3向右平移1个单位长度到B1B2B3,得到封闭图形A1A2A3B3B2B1(阴影部分),则S阴影= 。
(
B
2
B
1
A
2
A
1
B
3
B
1
A
3
A
1
A
2
B
2
草地
草地
小路
图
①
图
③
图
②
)(3)在图③中,在一块长方形草地上,有一条弯弯曲曲的小路,(小路任何地方的水平宽度都是1个单位长度),请猜想小路的面积是多少?
【作业A组】
1.如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论中错误的
是( ) A.△ABC≌△DEF B.∠DEF=90° C.AC=DF D.EC=CF
2.如图,若△DEF是由△ABC经过平移后得到的,则平移的距离是( )
A.线段BC的长度 B.线段BE的长度 C.线段EC的长度 D.线段EF的长度
1题图 2题图 3题图 4题图
3.如图,某宾馆准备在大厅的楼梯上铺上某种红色地毯,已知这种地毯每平方米售价30元,主楼梯道宽2米,其侧面如图所示,则购买地毯至少需要元 .
4. 如图所示,在四边形ABCD中,AD‖BC,BC>AD,∠B与∠C 互余,将AB,CD分别平移到EF和EG的位置,则△EFG为 三角形,若AD=2cm,BC=8cm,则FG= cm.
5. 如图,△BEF是由△ABC平移所得,点A,B,E在同一直 线上,若∠C=20°,∠ABC=68°,则∠CBF= 度
6.如图,已知△ABC的面积为16,BC=8.现将△ABC沿直线BC向右平移a个单位到△DEF的位置.
(1)当a=4时,求△ABC所扫过的面积;
(2)连接AE、AD,设AB=5,当DE=AD时,求a的值.
【作业B组】
1.将长度为3cm的线段向上平移20cm,所得线段的长度是( )
A.3cm B.23cm C.20cm D.17cm
2.如图,将△ABC沿BC方向平移2cm得到△DEF,若 △ABC的周长为16cm则四边形ABFD的周长为( ) A.16 cm B.18 cm C.20cm D.22cm
(
2
题图
3
题图
4
题图
)
3.如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当它移动的距离AA′等于4时,两个三角形重叠部分的面积为 .
4.如图,边长为4cm的正方形ABCD先向上平移2cm,再向右平移1cm,得到正方形A′B′C′D′,此时阴影部分的面积为 cm.
5.如图,边长为1的网格中有一个“柳叶”形图形,它是
由弧DG和弧EB和线段DE、GB围成的,两条弧的圆心
分别是点F和点A,半径都等于4,则“柳叶”形的面
积为 。
(
E
D
C
B
A
┘
)6、四边形ABCD中,AB‖CD,AC⊥BD,沿CD方向将线段BD平移到EC,平移的距离等于线段DC的长,连接BE。
(1)AC与CE是否垂直?为什么?
(2)△ACD与△BEC的面积是否相等?为什么?
(3)已知AC=a,BD=b,求梯形ABCD的面积。
(
4
) 第 页
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
