青岛版八年级数学下册11.2图形的旋转(第三课时)课件(共18张PPT)
文档属性
| 名称 | 青岛版八年级数学下册11.2图形的旋转(第三课时)课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
第11章 图形的平移与旋转
§11.2 图形的旋转 (3)
教学目标
1.通过实际操作,感受旋转变化中的不变量,发展学生的空间观念,体会数形结合的思想。
2.欣赏旋转在现实生活中的应用,培养学生分析问题和解决问题的能力
旋转的定义
在平面内,将一个图形绕一个定点按某一个方向(逆时针或顺时针方向)转动一定的角度,这样的变换叫做图形的旋转,这个定点叫做旋转中心,这个角叫做旋转角旋转后图形的位置是由旋转中心、旋转方向和旋转角确定的。
知 识 链 接
对应点到旋转中心的距离相等;
两组对应点分别与旋转中心的连线所成的角相等。
一个图形和它经过旋转所得到的图形中,
旋转的性质
(旋转角相等)
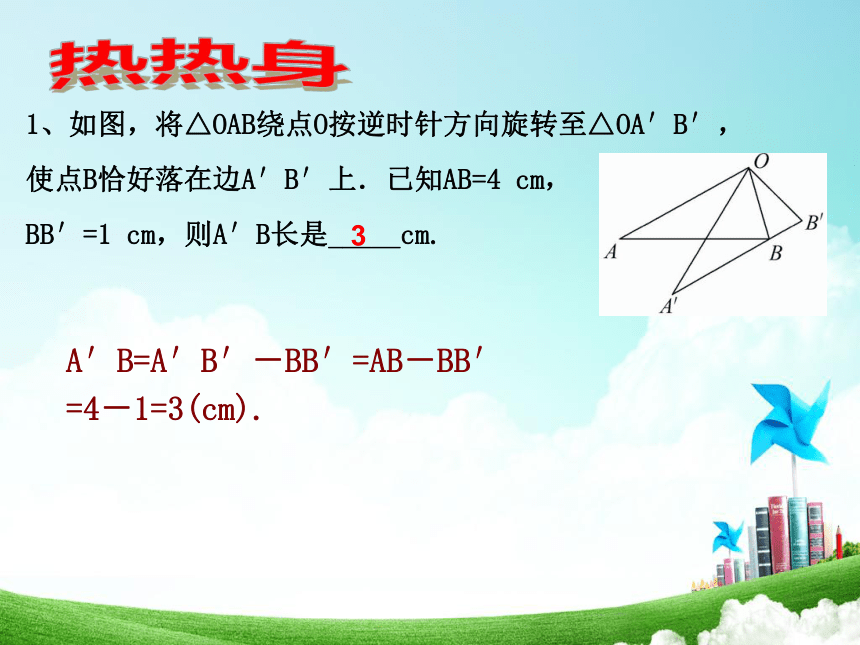
1、如图,将△OAB绕点O按逆时针方向旋转至△OA′B′,使点B恰好落在边A′B′上.已知AB=4 cm,
BB′=1 cm,则A′B长是_____cm.
A′B=A′B′-BB′=AB-BB′
=4-1=3(cm).
3
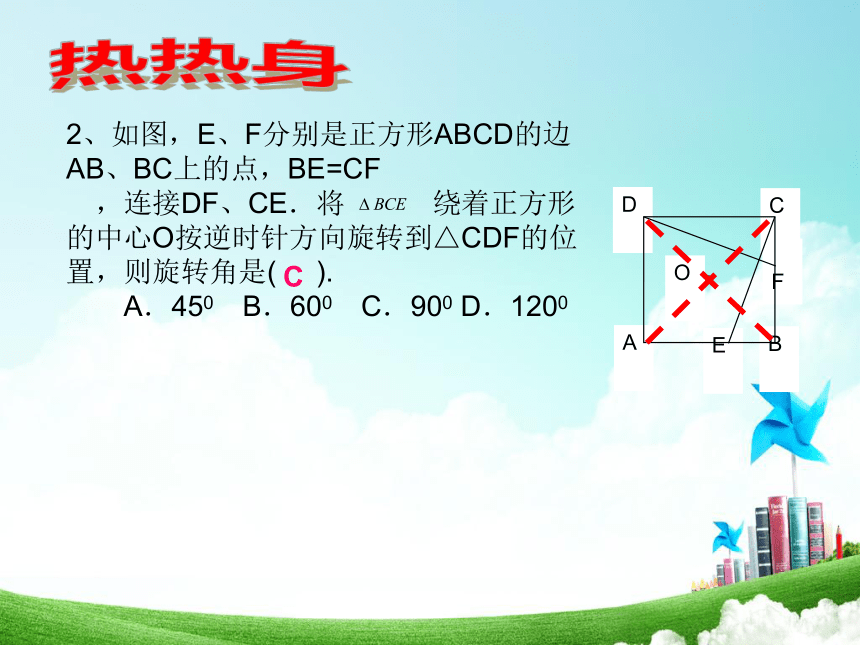
2、如图,E、F分别是正方形ABCD的边AB、BC上的点,BE=CF
,连接DF、CE.将 绕着正方形的中心O按逆时针方向旋转到△CDF的位置,则旋转角是( ).
A.450 B.600 C.900 D.1200
B
E
F
C
A
D
O
C
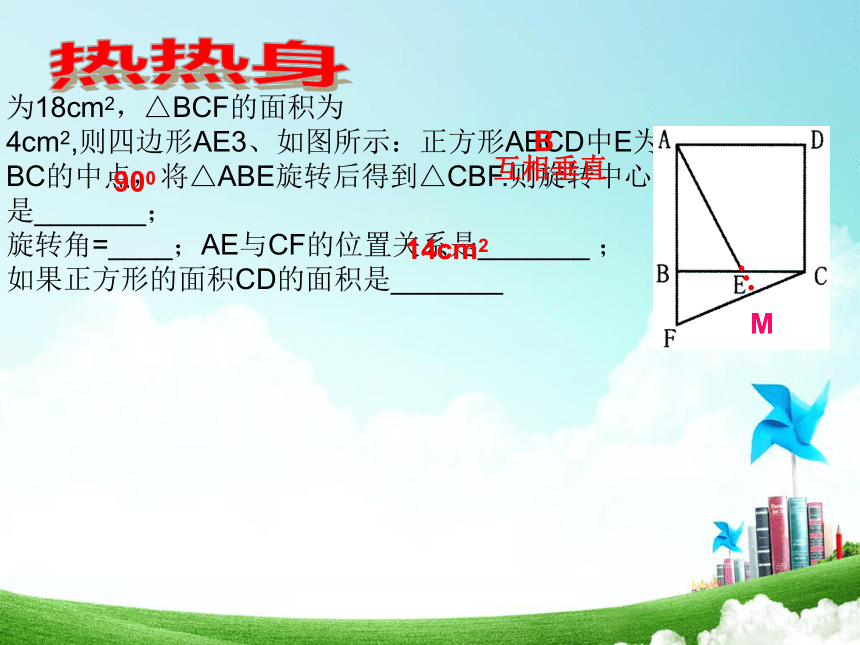
为18cm2,△BCF的面积为
4cm2,则四边形AE3、如图所示:正方形ABCD中E为BC的中点,将△ABE旋转后得到△CBF.则旋转中心是_______;
旋转角=____;AE与CF的位置关系是_______ ;
如果正方形的面积CD的面积是_______
B
900
互相垂直
14cm2
M
∟
F
E
C
B
O
A
典例 探究
在直角三角尺按(2)中的方式旋转时,Rt⊿ ABC中,∠B= ∠OAF=45°,OB=OA,总有∠BOE= ∠AOF,因而总有⊿ OBE≌ ⊿ OAF,所以BE=AF,OE=OF, 从而AE=CF
A
B
D
C
E
F
G
①
典例 探究
解(1) 在⊿ BDG与⊿ ADE中,
∵BD=AD,GD=DE,
∠GDB= ∠EDA= 90°
∴Rt⊿BDG≌ Rt⊿ADE(SAS)
∴BG=AE
A
B
D
C
E
F
G
①
B
C
A
D
F
E
G
B
C
A
F
G
E
D
1、如图,在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转900得到△DCF,连结EF,若∠BEC=600,则∠EFD的度数为( )A.100 B.150 C.200 D.250
2、如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为 .
小试牛刀
B
A
B
C
D
D`
3、如图,D是等腰直角三角形ABC内一点,BC是斜边,如果将⊿ABD绕点A按逆时针方向旋转到⊿ABD`的位置,则∠ADD`=( )
A. 45° B . 48° C .30° D.60°
小试牛刀
A
A
B
C
D
如图,把正方形ABCD绕点A按顺时针方向旋转,得到正方形AEFG,边FG与BC交于点H,线段HG与HB相等吗?说明你的理由。
E
H
G
F
大显身手
相等,HL.
课堂小结
通过本节课的学习,你有哪些收获呢?
还存在哪些不足的地方?
2、已知四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF。
(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积。
(3)解:由旋转性质得 ∠FAE=∠BAD=90°,AE=AF △AEF为等腰直角三角形。
∴ S△AEF = 1/2AE●AF
= AE●AE= 1/2 AE2.
若BC=8,DE=6,则AD=BC=8,AE=10
∴S△AEF= 1/2 AE2 = 1/2 ×102 =50
答:△AEF的面积为50平方单位。
作业
1、课本P181 第1、2题;
A
90
第11章 图形的平移与旋转
§11.2 图形的旋转 (3)
教学目标
1.通过实际操作,感受旋转变化中的不变量,发展学生的空间观念,体会数形结合的思想。
2.欣赏旋转在现实生活中的应用,培养学生分析问题和解决问题的能力
旋转的定义
在平面内,将一个图形绕一个定点按某一个方向(逆时针或顺时针方向)转动一定的角度,这样的变换叫做图形的旋转,这个定点叫做旋转中心,这个角叫做旋转角旋转后图形的位置是由旋转中心、旋转方向和旋转角确定的。
知 识 链 接
对应点到旋转中心的距离相等;
两组对应点分别与旋转中心的连线所成的角相等。
一个图形和它经过旋转所得到的图形中,
旋转的性质
(旋转角相等)
1、如图,将△OAB绕点O按逆时针方向旋转至△OA′B′,使点B恰好落在边A′B′上.已知AB=4 cm,
BB′=1 cm,则A′B长是_____cm.
A′B=A′B′-BB′=AB-BB′
=4-1=3(cm).
3
2、如图,E、F分别是正方形ABCD的边AB、BC上的点,BE=CF
,连接DF、CE.将 绕着正方形的中心O按逆时针方向旋转到△CDF的位置,则旋转角是( ).
A.450 B.600 C.900 D.1200
B
E
F
C
A
D
O
C
为18cm2,△BCF的面积为
4cm2,则四边形AE3、如图所示:正方形ABCD中E为BC的中点,将△ABE旋转后得到△CBF.则旋转中心是_______;
旋转角=____;AE与CF的位置关系是_______ ;
如果正方形的面积CD的面积是_______
B
900
互相垂直
14cm2
M
∟
F
E
C
B
O
A
典例 探究
在直角三角尺按(2)中的方式旋转时,Rt⊿ ABC中,∠B= ∠OAF=45°,OB=OA,总有∠BOE= ∠AOF,因而总有⊿ OBE≌ ⊿ OAF,所以BE=AF,OE=OF, 从而AE=CF
A
B
D
C
E
F
G
①
典例 探究
解(1) 在⊿ BDG与⊿ ADE中,
∵BD=AD,GD=DE,
∠GDB= ∠EDA= 90°
∴Rt⊿BDG≌ Rt⊿ADE(SAS)
∴BG=AE
A
B
D
C
E
F
G
①
B
C
A
D
F
E
G
B
C
A
F
G
E
D
1、如图,在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转900得到△DCF,连结EF,若∠BEC=600,则∠EFD的度数为( )A.100 B.150 C.200 D.250
2、如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为 .
小试牛刀
B
A
B
C
D
D`
3、如图,D是等腰直角三角形ABC内一点,BC是斜边,如果将⊿ABD绕点A按逆时针方向旋转到⊿ABD`的位置,则∠ADD`=( )
A. 45° B . 48° C .30° D.60°
小试牛刀
A
A
B
C
D
如图,把正方形ABCD绕点A按顺时针方向旋转,得到正方形AEFG,边FG与BC交于点H,线段HG与HB相等吗?说明你的理由。
E
H
G
F
大显身手
相等,HL.
课堂小结
通过本节课的学习,你有哪些收获呢?
还存在哪些不足的地方?
2、已知四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF。
(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积。
(3)解:由旋转性质得 ∠FAE=∠BAD=90°,AE=AF △AEF为等腰直角三角形。
∴ S△AEF = 1/2AE●AF
= AE●AE= 1/2 AE2.
若BC=8,DE=6,则AD=BC=8,AE=10
∴S△AEF= 1/2 AE2 = 1/2 ×102 =50
答:△AEF的面积为50平方单位。
作业
1、课本P181 第1、2题;
A
90
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
