沪科版数学七年级下册 10.3 平行线的性质 课件(共11张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 10.3 平行线的性质 课件(共11张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 123.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-17 20:19:22 | ||
图片预览


文档简介
(共11张PPT)
10.3 平行线的性质
情境引入
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
平行线的判定
上节课学的平行线的判定有哪些?
合作探究
b
a
c
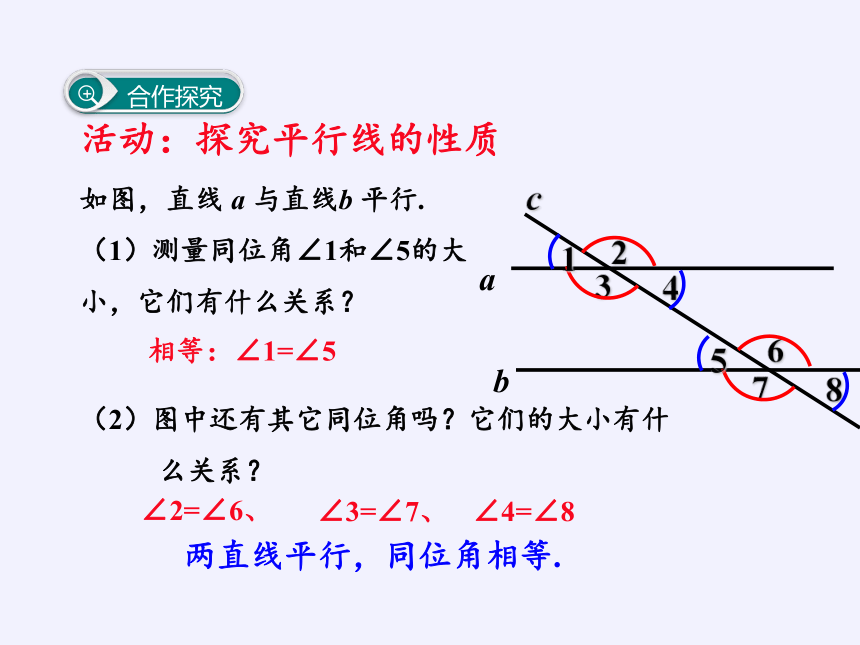
如图,直线 a 与直线b 平行.
(1)测量同位角∠1和∠5的大
小,它们有什么关系?
相等:∠1=∠5
∠2=∠6、
∠3=∠7、
∠4=∠8
8
3
2
1
4
6
7
5
两直线平行,同位角相等.
(2)图中还有其它同位角吗?它们的大小有什
么关系?
活动:探究平行线的性质
b
a
c
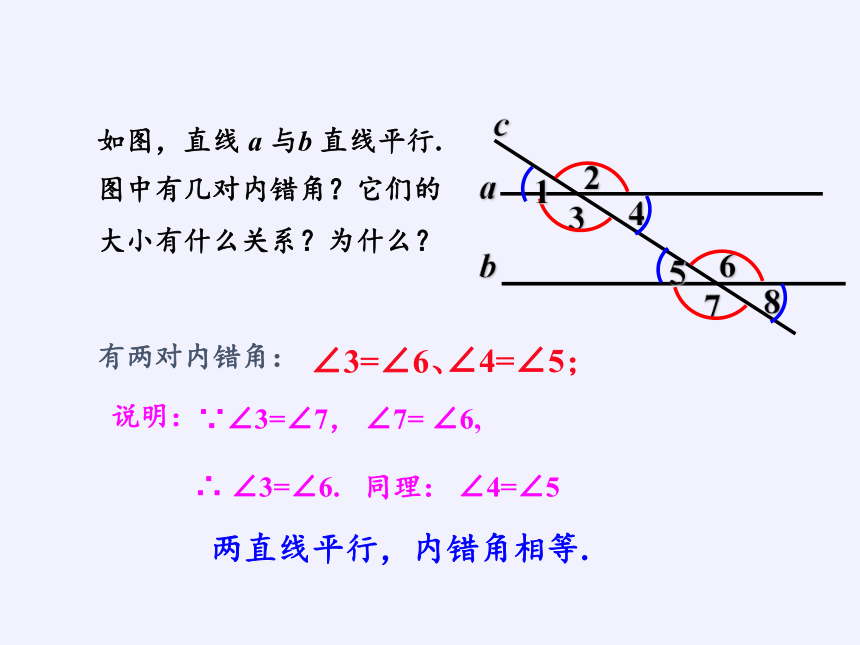
如图,直线 a 与b 直线平行.
图中有几对内错角?它们的大小有什么关系?为什么?
有两对内错角:
∠3=∠6、
∠4=∠5;
∵∠3=∠7, ∠7= ∠6,
同理: ∠4=∠5
8
3
2
1
4
6
7
5
两直线平行,内错角相等.
∴ ∠3=∠6.
说明:
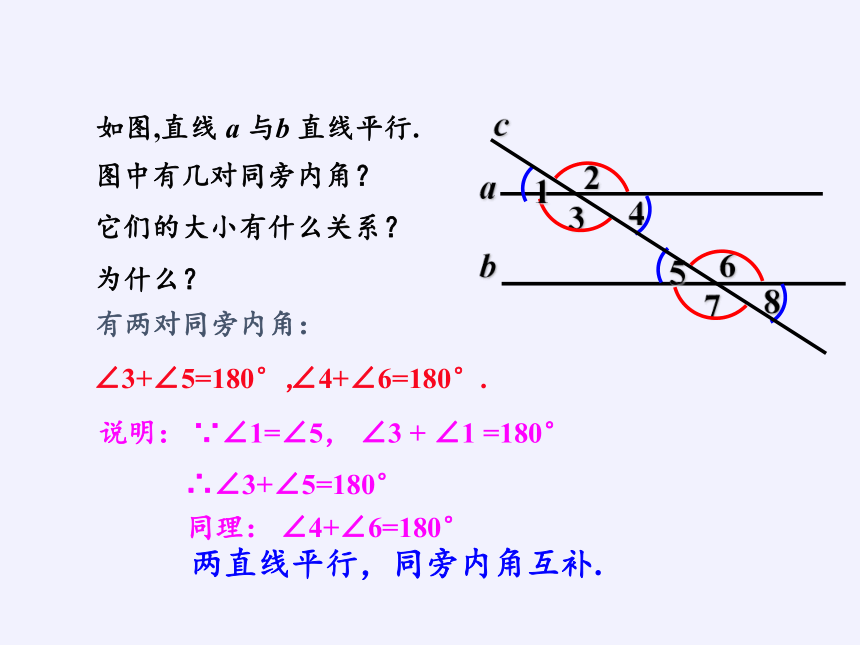
如图,直线 a 与b 直线平行.
图中有几对同旁内角?
它们的大小有什么关系?
为什么?
有两对同旁内角:
∠3+∠5=180°,
∠4+∠6=180°.
说明: ∵∠1=∠5, ∠3 + ∠1 =180°
∴∠3+∠5=180°
同理: ∠4+∠6=180°
两直线平行,同旁内角互补.
b
a
c
8
3
2
1
4
6
7
5
1.如果AD//BC,可得∠B=∠1,
根据__________________________.
2.如果AB//CD,根据两直线平行,内错角相等可得∠ = ∠__
3.如果AD//BC,根据___________________________.
可得∠C+_______=180 .
A
B
C
D
1
两直线平行,同位角相等
D
1
两直线平行,同旁内角互补
∠D
平行线的性质:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补.
课堂小结
1.如图, AB、CD被EF所截,AB∥CD.
若∠1=120° 则∠2= __
( )
∠3= __ -∠1=___
( )
60°
A
B
C
D
E
F
1
2
3
120 °
两直线平行,内错角相等
180°
两直线平行,同旁内角互补
随堂训练
2. 如图,一束平行光线AB和DE射向一个水平镜面后被反射,
(1)∠1,∠3的大小有什么关系?
∠2与∠4呢?
∵AB∥DE
∴∠1=∠3
相等:∠1=∠3;
(2)反射光线BC与EF也平行吗?
∵ ∠2=∠4 ∴ BC∥EF
平行:
又∵∠1=∠2 ,
3=∠4
∴ ∠2=∠4
A
B
D
E
C
F
此时∠1=∠2 , ∠3=∠4 .
1
3
2
4
∠2 =∠4 .
3.如图所示,AB∥CD,AC∥BD.分别找出与∠1相等或互补的角.
如图,与∠1相等的角有:
与∠1互补的角有:
1
A
B
D
C
7个
8个
谢 谢
10.3 平行线的性质
情境引入
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
平行线的判定
上节课学的平行线的判定有哪些?
合作探究
b
a
c
如图,直线 a 与直线b 平行.
(1)测量同位角∠1和∠5的大
小,它们有什么关系?
相等:∠1=∠5
∠2=∠6、
∠3=∠7、
∠4=∠8
8
3
2
1
4
6
7
5
两直线平行,同位角相等.
(2)图中还有其它同位角吗?它们的大小有什
么关系?
活动:探究平行线的性质
b
a
c
如图,直线 a 与b 直线平行.
图中有几对内错角?它们的大小有什么关系?为什么?
有两对内错角:
∠3=∠6、
∠4=∠5;
∵∠3=∠7, ∠7= ∠6,
同理: ∠4=∠5
8
3
2
1
4
6
7
5
两直线平行,内错角相等.
∴ ∠3=∠6.
说明:
如图,直线 a 与b 直线平行.
图中有几对同旁内角?
它们的大小有什么关系?
为什么?
有两对同旁内角:
∠3+∠5=180°,
∠4+∠6=180°.
说明: ∵∠1=∠5, ∠3 + ∠1 =180°
∴∠3+∠5=180°
同理: ∠4+∠6=180°
两直线平行,同旁内角互补.
b
a
c
8
3
2
1
4
6
7
5
1.如果AD//BC,可得∠B=∠1,
根据__________________________.
2.如果AB//CD,根据两直线平行,内错角相等可得∠ = ∠__
3.如果AD//BC,根据___________________________.
可得∠C+_______=180 .
A
B
C
D
1
两直线平行,同位角相等
D
1
两直线平行,同旁内角互补
∠D
平行线的性质:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补.
课堂小结
1.如图, AB、CD被EF所截,AB∥CD.
若∠1=120° 则∠2= __
( )
∠3= __ -∠1=___
( )
60°
A
B
C
D
E
F
1
2
3
120 °
两直线平行,内错角相等
180°
两直线平行,同旁内角互补
随堂训练
2. 如图,一束平行光线AB和DE射向一个水平镜面后被反射,
(1)∠1,∠3的大小有什么关系?
∠2与∠4呢?
∵AB∥DE
∴∠1=∠3
相等:∠1=∠3;
(2)反射光线BC与EF也平行吗?
∵ ∠2=∠4 ∴ BC∥EF
平行:
又∵∠1=∠2 ,
3=∠4
∴ ∠2=∠4
A
B
D
E
C
F
此时∠1=∠2 , ∠3=∠4 .
1
3
2
4
∠2 =∠4 .
3.如图所示,AB∥CD,AC∥BD.分别找出与∠1相等或互补的角.
如图,与∠1相等的角有:
与∠1互补的角有:
1
A
B
D
C
7个
8个
谢 谢
