江西省上饶市横峰中学2013届高三第一次联考数学(文)试题
文档属性
| 名称 | 江西省上饶市横峰中学2013届高三第一次联考数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 307.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-26 22:32:31 | ||
图片预览




文档简介
上饶市横峰中学2013届高三第一次联考数学(文 )试题
本试卷分第I卷和第II卷两部分.满分150分.考试用时120分钟.
第I卷(共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设是虚数单位,则( )
A. B. C. D.
2.设全集,,,则( )
A. B. C. D.
5.已知直线的方程,圆的方程为,则直线的位置关系是 ( )
A.相切 B.相交 C.相离 D.不能确定
6.已知分别为方程的解,则 的大小关系为( )
A. B. C. D.
7. 设双曲线的两个焦点分别为,点在双曲线上,且,,则该双曲线的离心率为( )
A. B. C. D.
8.如图甲所示,三棱锥的高分别在和上,且,图乙中的四个图像大致描绘了三棱锥的体积与的变化关系,其中正确的是( )
9.已知函数 数列满足,且是单调递增数列,则实数的取值范围是( )
A. B. C. D.
10.各项互不相等的有限正项数列,集合 ,集合,则集合中的元素至多有( )个.
A. B. C. D.
第Ⅱ卷(共90分)
二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中的横线上.
11.右边茎叶图表示的是甲、乙两人在次综合测评中的成绩,其中
一个数字被污损.则甲的平均成绩超过乙的平均成绩的概率为_____.
12. 已知都是正实数,函数的图象过点,则
的最小值是 .
13.已知中,,点在上,且,则 .
14.已知数列的前项和,则 .
15.给出以下五个命题:
①命题“对任意,”的否定是:“存在”;
②已知函数的图象经过点,则函数图象在点处切线的斜率等于;
③“”是“直线与直线垂直”的充要条件;
④设为两个不同的平面,直线,则是 成立的充分不必要条件;
⑤已知向量与向量的夹角为锐角,那么实数的取值范围是.
其中正确命题的序号是 .
三、解答题:本大题共6小题,共75分.解答应写出必要的文字说明、证明过程及演算步骤.
16. (本小题满分12分)
已知向量,向量,函数.
(1)求函数的对称轴方程及单调递增区间;
(2)在锐角中,若,求的值.
17. (本小题满分12分)
已知点是满足约束条件的有序实数对.
(1)求满足上述条件点个数,并列举出来;
(2)若点 也满足上述条件(不重合)求的概率.
19. (本小题满分12分)
设等比数列的前项和为,已知.
(1)求数列的通项公式;
(2)在与之间插入个数,使这个数组成公差为的等差数列,求数列的前项和.
20. (本小题满分13分)
已知函数 提示:.
(1)设,讨论函数的单调性;
(2)若对任意的,恒有,求的取值范围.
21. (本小题满分14分)
已知椭圆(的一个焦点是,且过点.
(1)求椭圆的方程.
(2)设椭圆与轴的两个交点为,点上,直线分别与椭圆交于两点,试问当点上运动时,直线是否恒经过定点?若存在求出点坐标,若不存在,请说明理由.
2013届高三第一次联考
数学试题(文)
参考答案与评分标准
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
三、解答题:本大题共6小题,共75分.解答应写出必要的文字说明、证明过程及演算步骤.
17. (本小题满分12分)
依题意 当 故点坐标有6个,分别是.
…………………………………5分
(2)基本事件共有15个. (取
当;当;
当;当;当
共有5对 与,与,与,与,与
故.………………………12分
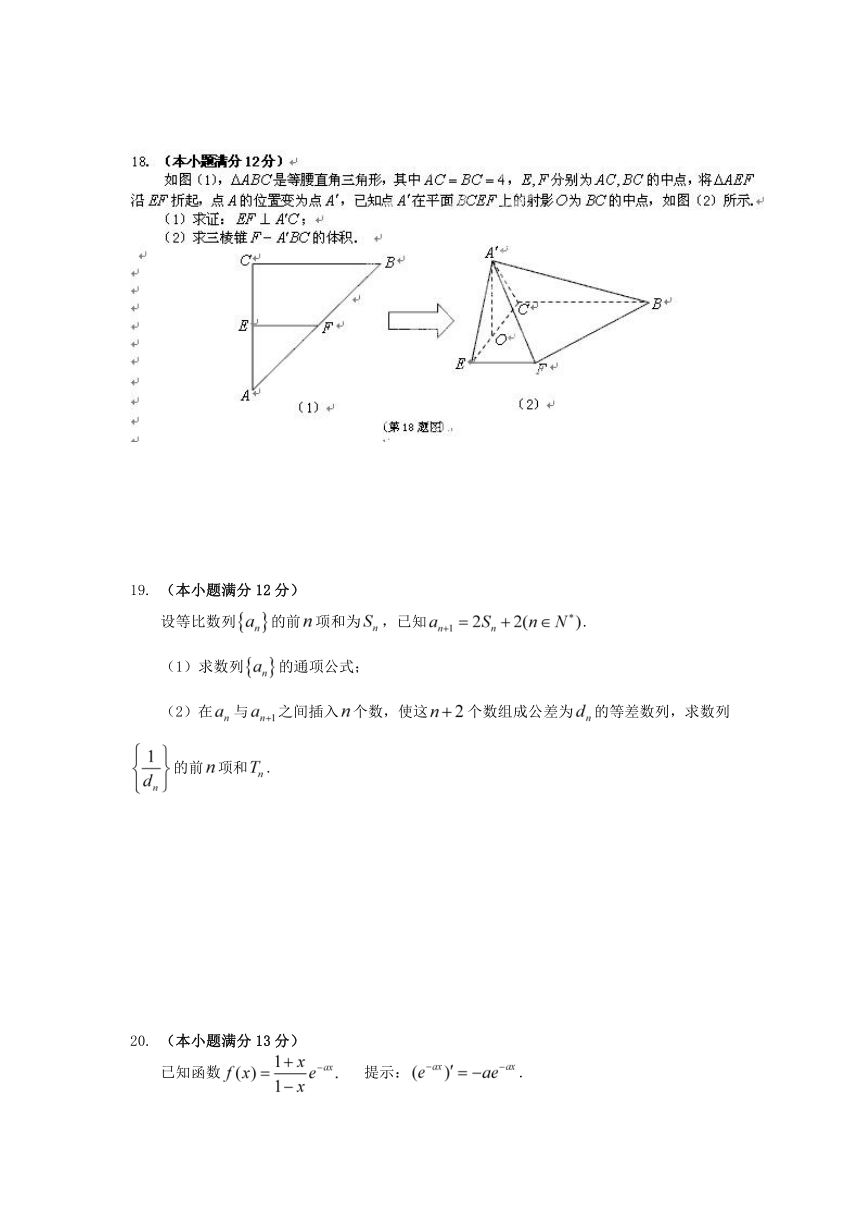
18. (本小题满分12分)
【解】(1)证法一:在中,是等腰直角的中位线,
在四棱锥中,,, 平面,
又平面, ……………………………6分
证法二:同证法一
平面,
又平面, ……………………………6分
(2)在直角梯形中 ,
, =
又垂直平分, …………9分
三棱锥的体积为:……12分
20. (本小题满分13分)
【解】(1),…………………2分
时,增区间为,,无减区间;……………4分
时,增区间为,,,减区间为.
……………………6分
(2) 时,在上单调递增,;……………7分
时,;…………………………9分
时, 在上递减,在上递增, ,而,故.…………………12分
综上,时, 对任意的,恒有.…………………13分
21. (本小题满分14分)
【解】(1)依题意可得,椭圆的方程……4分
(2)点上运动,,
,若存在直线恒经过定点,则点必在轴上.…………………………………………6分
设,则,设,由……..①
……..②
由①②=,=.………………………8分
则,设,
…………..③
……. ④ 由③④=,=.……………10分
设,,,,
三点共线 ()--()()=0
--=0
=0
,故存在点 ………………………14分
上饶市横峰中学2013届高三第一次联考数学(文 )试题
本试卷分第I卷和第II卷两部分.满分150分.考试用时120分钟.
第I卷(共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设是虚数单位,则( )
A. B. C. D.
2.设全集,,,则( )
A. B. C. D.
5.已知直线的方程,圆的方程为,则直线的位置关系是 ( )
A.相切 B.相交 C.相离 D.不能确定
6.已知分别为方程的解,则 的大小关系为( )
A. B. C. D.
7. 设双曲线的两个焦点分别为,点在双曲线上,且,,则该双曲线的离心率为( )
A. B. C. D.
8.如图甲所示,三棱锥的高分别在和上,且,图乙中的四个图像大致描绘了三棱锥的体积与的变化关系,其中正确的是( )
9.已知函数 数列满足,且是单调递增数列,则实数的取值范围是( )
A. B. C. D.
10.各项互不相等的有限正项数列,集合 ,集合,则集合中的元素至多有( )个.
A. B. C. D.
第Ⅱ卷(共90分)
二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中的横线上.
11.右边茎叶图表示的是甲、乙两人在次综合测评中的成绩,其中
一个数字被污损.则甲的平均成绩超过乙的平均成绩的概率为_____.
12. 已知都是正实数,函数的图象过点,则
的最小值是 .
13.已知中,,点在上,且,则 .
14.已知数列的前项和,则 .
15.给出以下五个命题:
①命题“对任意,”的否定是:“存在”;
②已知函数的图象经过点,则函数图象在点处切线的斜率等于;
③“”是“直线与直线垂直”的充要条件;
④设为两个不同的平面,直线,则是 成立的充分不必要条件;
⑤已知向量与向量的夹角为锐角,那么实数的取值范围是.
其中正确命题的序号是 .
三、解答题:本大题共6小题,共75分.解答应写出必要的文字说明、证明过程及演算步骤.
16. (本小题满分12分)
已知向量,向量,函数.
(1)求函数的对称轴方程及单调递增区间;
(2)在锐角中,若,求的值.
17. (本小题满分12分)
已知点是满足约束条件的有序实数对.
(1)求满足上述条件点个数,并列举出来;
(2)若点 也满足上述条件(不重合)求的概率.
19. (本小题满分12分)
设等比数列的前项和为,已知.
(1)求数列的通项公式;
(2)在与之间插入个数,使这个数组成公差为的等差数列,求数列的前项和.
20. (本小题满分13分)
已知函数 提示:.
(1)设,讨论函数的单调性;
(2)若对任意的,恒有,求的取值范围.
21. (本小题满分14分)
已知椭圆(的一个焦点是,且过点.
(1)求椭圆的方程.
(2)设椭圆与轴的两个交点为,点上,直线分别与椭圆交于两点,试问当点上运动时,直线是否恒经过定点?若存在求出点坐标,若不存在,请说明理由.
2013届高三第一次联考
数学试题(文)
参考答案与评分标准
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
三、解答题:本大题共6小题,共75分.解答应写出必要的文字说明、证明过程及演算步骤.
17. (本小题满分12分)
依题意 当 故点坐标有6个,分别是.
…………………………………5分
(2)基本事件共有15个. (取
当;当;
当;当;当
共有5对 与,与,与,与,与
故.………………………12分
18. (本小题满分12分)
【解】(1)证法一:在中,是等腰直角的中位线,
在四棱锥中,,, 平面,
又平面, ……………………………6分
证法二:同证法一
平面,
又平面, ……………………………6分
(2)在直角梯形中 ,
, =
又垂直平分, …………9分
三棱锥的体积为:……12分
20. (本小题满分13分)
【解】(1),…………………2分
时,增区间为,,无减区间;……………4分
时,增区间为,,,减区间为.
……………………6分
(2) 时,在上单调递增,;……………7分
时,;…………………………9分
时, 在上递减,在上递增, ,而,故.…………………12分
综上,时, 对任意的,恒有.…………………13分
21. (本小题满分14分)
【解】(1)依题意可得,椭圆的方程……4分
(2)点上运动,,
,若存在直线恒经过定点,则点必在轴上.…………………………………………6分
设,则,设,由……..①
……..②
由①②=,=.………………………8分
则,设,
…………..③
……. ④ 由③④=,=.……………10分
设,,,,
三点共线 ()--()()=0
--=0
=0
,故存在点 ………………………14分
本试卷分第I卷和第II卷两部分.满分150分.考试用时120分钟.
第I卷(共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设是虚数单位,则( )
A. B. C. D.
2.设全集,,,则( )
A. B. C. D.
5.已知直线的方程,圆的方程为,则直线的位置关系是 ( )
A.相切 B.相交 C.相离 D.不能确定
6.已知分别为方程的解,则 的大小关系为( )
A. B. C. D.
7. 设双曲线的两个焦点分别为,点在双曲线上,且,,则该双曲线的离心率为( )
A. B. C. D.
8.如图甲所示,三棱锥的高分别在和上,且,图乙中的四个图像大致描绘了三棱锥的体积与的变化关系,其中正确的是( )
9.已知函数 数列满足,且是单调递增数列,则实数的取值范围是( )
A. B. C. D.
10.各项互不相等的有限正项数列,集合 ,集合,则集合中的元素至多有( )个.
A. B. C. D.
第Ⅱ卷(共90分)
二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中的横线上.
11.右边茎叶图表示的是甲、乙两人在次综合测评中的成绩,其中
一个数字被污损.则甲的平均成绩超过乙的平均成绩的概率为_____.
12. 已知都是正实数,函数的图象过点,则
的最小值是 .
13.已知中,,点在上,且,则 .
14.已知数列的前项和,则 .
15.给出以下五个命题:
①命题“对任意,”的否定是:“存在”;
②已知函数的图象经过点,则函数图象在点处切线的斜率等于;
③“”是“直线与直线垂直”的充要条件;
④设为两个不同的平面,直线,则是 成立的充分不必要条件;
⑤已知向量与向量的夹角为锐角,那么实数的取值范围是.
其中正确命题的序号是 .
三、解答题:本大题共6小题,共75分.解答应写出必要的文字说明、证明过程及演算步骤.
16. (本小题满分12分)
已知向量,向量,函数.
(1)求函数的对称轴方程及单调递增区间;
(2)在锐角中,若,求的值.
17. (本小题满分12分)
已知点是满足约束条件的有序实数对.
(1)求满足上述条件点个数,并列举出来;
(2)若点 也满足上述条件(不重合)求的概率.
19. (本小题满分12分)
设等比数列的前项和为,已知.
(1)求数列的通项公式;
(2)在与之间插入个数,使这个数组成公差为的等差数列,求数列的前项和.
20. (本小题满分13分)
已知函数 提示:.
(1)设,讨论函数的单调性;
(2)若对任意的,恒有,求的取值范围.
21. (本小题满分14分)
已知椭圆(的一个焦点是,且过点.
(1)求椭圆的方程.
(2)设椭圆与轴的两个交点为,点上,直线分别与椭圆交于两点,试问当点上运动时,直线是否恒经过定点?若存在求出点坐标,若不存在,请说明理由.
2013届高三第一次联考
数学试题(文)
参考答案与评分标准
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
三、解答题:本大题共6小题,共75分.解答应写出必要的文字说明、证明过程及演算步骤.
17. (本小题满分12分)
依题意 当 故点坐标有6个,分别是.
…………………………………5分
(2)基本事件共有15个. (取
当;当;
当;当;当
共有5对 与,与,与,与,与
故.………………………12分
18. (本小题满分12分)
【解】(1)证法一:在中,是等腰直角的中位线,
在四棱锥中,,, 平面,
又平面, ……………………………6分
证法二:同证法一
平面,
又平面, ……………………………6分
(2)在直角梯形中 ,
, =
又垂直平分, …………9分
三棱锥的体积为:……12分
20. (本小题满分13分)
【解】(1),…………………2分
时,增区间为,,无减区间;……………4分
时,增区间为,,,减区间为.
……………………6分
(2) 时,在上单调递增,;……………7分
时,;…………………………9分
时, 在上递减,在上递增, ,而,故.…………………12分
综上,时, 对任意的,恒有.…………………13分
21. (本小题满分14分)
【解】(1)依题意可得,椭圆的方程……4分
(2)点上运动,,
,若存在直线恒经过定点,则点必在轴上.…………………………………………6分
设,则,设,由……..①
……..②
由①②=,=.………………………8分
则,设,
…………..③
……. ④ 由③④=,=.……………10分
设,,,,
三点共线 ()--()()=0
--=0
=0
,故存在点 ………………………14分
上饶市横峰中学2013届高三第一次联考数学(文 )试题
本试卷分第I卷和第II卷两部分.满分150分.考试用时120分钟.
第I卷(共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设是虚数单位,则( )
A. B. C. D.
2.设全集,,,则( )
A. B. C. D.
5.已知直线的方程,圆的方程为,则直线的位置关系是 ( )
A.相切 B.相交 C.相离 D.不能确定
6.已知分别为方程的解,则 的大小关系为( )
A. B. C. D.
7. 设双曲线的两个焦点分别为,点在双曲线上,且,,则该双曲线的离心率为( )
A. B. C. D.
8.如图甲所示,三棱锥的高分别在和上,且,图乙中的四个图像大致描绘了三棱锥的体积与的变化关系,其中正确的是( )
9.已知函数 数列满足,且是单调递增数列,则实数的取值范围是( )
A. B. C. D.
10.各项互不相等的有限正项数列,集合 ,集合,则集合中的元素至多有( )个.
A. B. C. D.
第Ⅱ卷(共90分)
二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中的横线上.
11.右边茎叶图表示的是甲、乙两人在次综合测评中的成绩,其中
一个数字被污损.则甲的平均成绩超过乙的平均成绩的概率为_____.
12. 已知都是正实数,函数的图象过点,则
的最小值是 .
13.已知中,,点在上,且,则 .
14.已知数列的前项和,则 .
15.给出以下五个命题:
①命题“对任意,”的否定是:“存在”;
②已知函数的图象经过点,则函数图象在点处切线的斜率等于;
③“”是“直线与直线垂直”的充要条件;
④设为两个不同的平面,直线,则是 成立的充分不必要条件;
⑤已知向量与向量的夹角为锐角,那么实数的取值范围是.
其中正确命题的序号是 .
三、解答题:本大题共6小题,共75分.解答应写出必要的文字说明、证明过程及演算步骤.
16. (本小题满分12分)
已知向量,向量,函数.
(1)求函数的对称轴方程及单调递增区间;
(2)在锐角中,若,求的值.
17. (本小题满分12分)
已知点是满足约束条件的有序实数对.
(1)求满足上述条件点个数,并列举出来;
(2)若点 也满足上述条件(不重合)求的概率.
19. (本小题满分12分)
设等比数列的前项和为,已知.
(1)求数列的通项公式;
(2)在与之间插入个数,使这个数组成公差为的等差数列,求数列的前项和.
20. (本小题满分13分)
已知函数 提示:.
(1)设,讨论函数的单调性;
(2)若对任意的,恒有,求的取值范围.
21. (本小题满分14分)
已知椭圆(的一个焦点是,且过点.
(1)求椭圆的方程.
(2)设椭圆与轴的两个交点为,点上,直线分别与椭圆交于两点,试问当点上运动时,直线是否恒经过定点?若存在求出点坐标,若不存在,请说明理由.
2013届高三第一次联考
数学试题(文)
参考答案与评分标准
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
三、解答题:本大题共6小题,共75分.解答应写出必要的文字说明、证明过程及演算步骤.
17. (本小题满分12分)
依题意 当 故点坐标有6个,分别是.
…………………………………5分
(2)基本事件共有15个. (取
当;当;
当;当;当
共有5对 与,与,与,与,与
故.………………………12分
18. (本小题满分12分)
【解】(1)证法一:在中,是等腰直角的中位线,
在四棱锥中,,, 平面,
又平面, ……………………………6分
证法二:同证法一
平面,
又平面, ……………………………6分
(2)在直角梯形中 ,
, =
又垂直平分, …………9分
三棱锥的体积为:……12分
20. (本小题满分13分)
【解】(1),…………………2分
时,增区间为,,无减区间;……………4分
时,增区间为,,,减区间为.
……………………6分
(2) 时,在上单调递增,;……………7分
时,;…………………………9分
时, 在上递减,在上递增, ,而,故.…………………12分
综上,时, 对任意的,恒有.…………………13分
21. (本小题满分14分)
【解】(1)依题意可得,椭圆的方程……4分
(2)点上运动,,
,若存在直线恒经过定点,则点必在轴上.…………………………………………6分
设,则,设,由……..①
……..②
由①②=,=.………………………8分
则,设,
…………..③
……. ④ 由③④=,=.……………10分
设,,,,
三点共线 ()--()()=0
--=0
=0
,故存在点 ………………………14分
同课章节目录
