沪科版数学八年级下19.2平行四边形 第4课时 平行四边形判定(二) (共25张PPT)
文档属性
| 名称 | 沪科版数学八年级下19.2平行四边形 第4课时 平行四边形判定(二) (共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 291.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 00:00:00 | ||
图片预览



文档简介
(共25张PPT)
19.2 平行四边形
第4课时 平行四边形的判定(二)
沪科版数学八年级下册
第19章 四边形
两组对边分别相等
两组对角分别相等
两组对边分别平行
一组对边平行且相等
四边形是平行四边形
从看边
从角看
已学的平行四边形的判定方法
知识回顾
四边形是平行四边形
对角线互相平分
从对角线看:
四边形是平行四边形
思 考
?
O
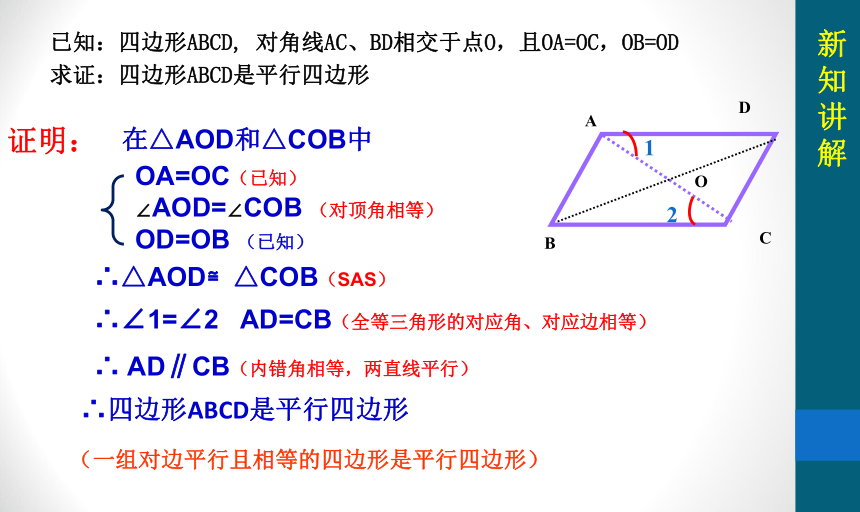
已知:四边形ABCD, 对角线AC、BD相交于点O,且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
证明:
在△AOD和△COB中
OA=OC(已知)
∠AOD=∠COB (对顶角相等)
OD=OB (已知)
∴△AOD≌△COB(SAS)
∴∠1=∠2 AD=CB(全等三角形的对应角、对应边相等)
∴ AD∥CB(内错角相等,两直线平行)
∴四边形ABCD是平行四边形
B
A
C
2
1
D
(一组对边平行且相等的四边形是平行四边形)
新知讲解
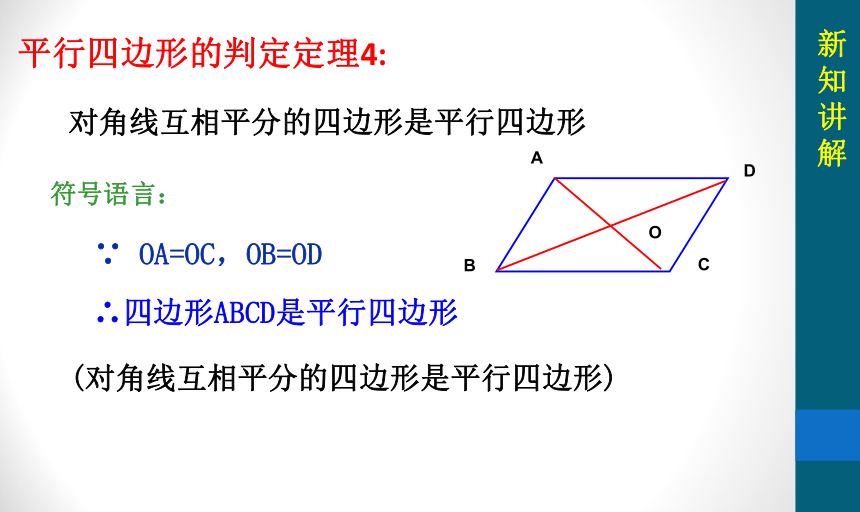
对角线互相平分的四边形是平行四边形
平行四边形的判定定理4:
符号语言:
A
B
C
D
O
∵ OA=OC,OB=OD
∴四边形ABCD是平行四边形
(对角线互相平分的四边形是平行四边形)
新知讲解
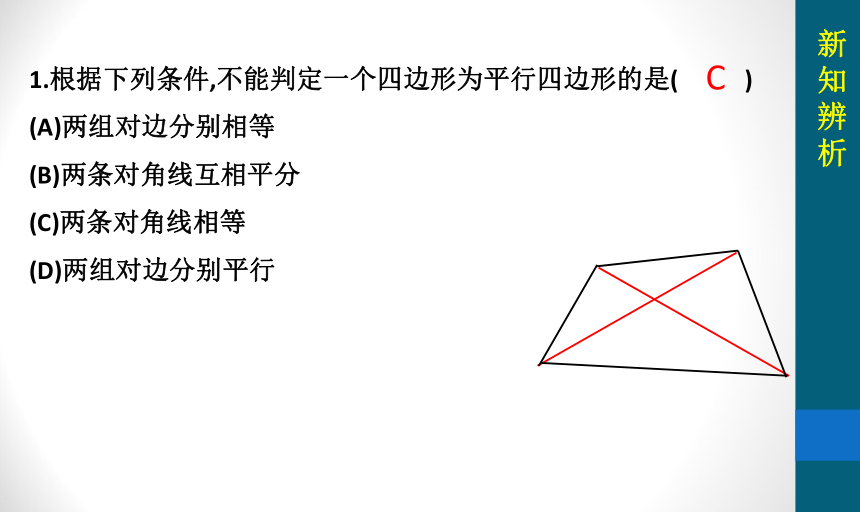
1.根据下列条件,不能判定一个四边形为平行四边形的是( )
(A)两组对边分别相等
(B)两条对角线互相平分
(C)两条对角线相等
(D)两组对边分别平行
C
新知辨析
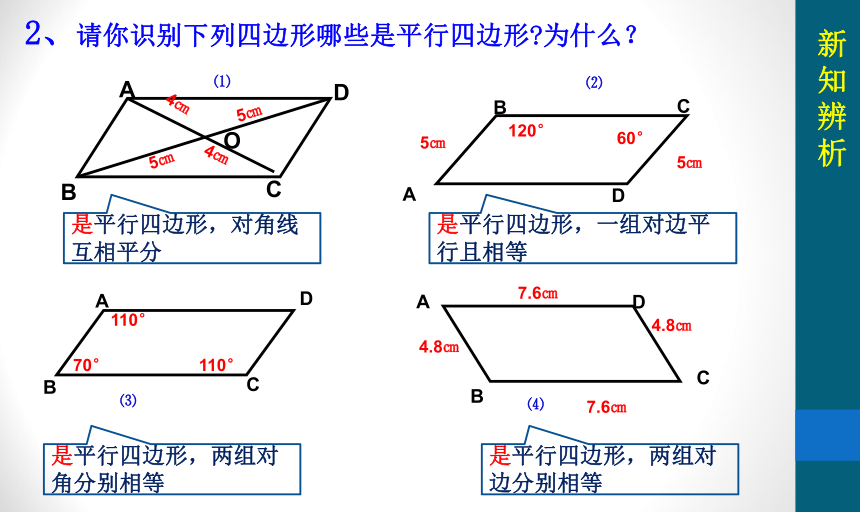
2、请你识别下列四边形哪些是平行四边形 为什么?
A
D
C
B
110°
70°
110°
⑴
⑷
⑶
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
⑵
7.6㎝
7.6㎝
新知辨析
是平行四边形,对角线互相平分
是平行四边形,一组对边平行且相等
是平行四边形,两组对角分别相等
是平行四边形,两组对边分别相等
3、判断
(1)一组对边平行且另一组对边相等的四边形是 平行四边形; ( )
(2)两组对角都相等的四边形是平行四边形 ( )
(3)一组对边平行且一组对角相等的四边形是平行边形; ( )
(4)一组对边平行,一组邻角互补的四边形是平行 四边形; ( )
(5)两组邻角互补的四边形是平行四边形. ( )
×
√
√
×
×
新知辨析
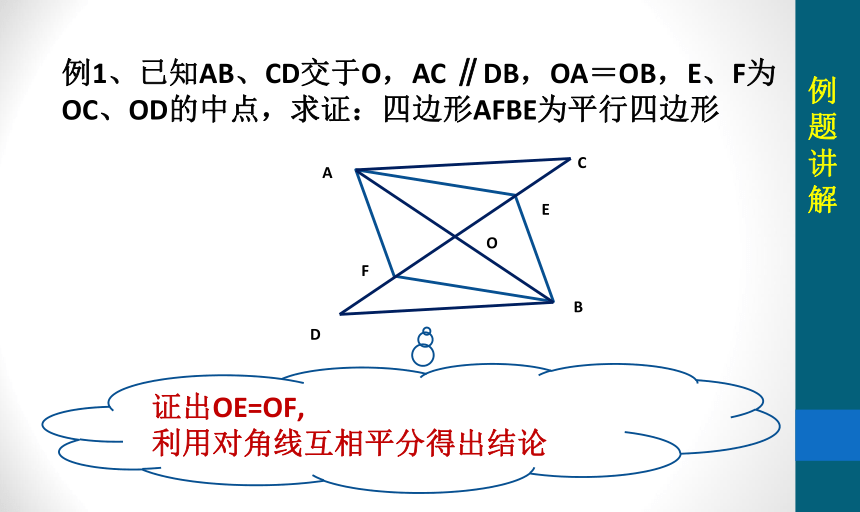
例1、已知AB、CD交于O,AC ∥DB,OA=OB,E、F为OC、OD的中点,求证:四边形AFBE为平行四边形
例题讲解
A
O
F
D
E
C
B
证出OE=OF,
利用对角线互相平分得出结论
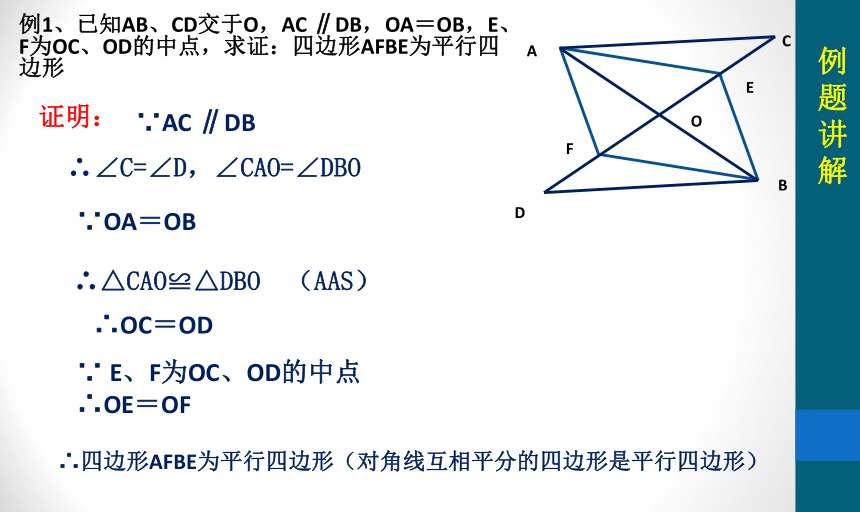
例1、已知AB、CD交于O,AC ∥DB,OA=OB,E、F为OC、OD的中点,求证:四边形AFBE为平行四边形
例题讲解
A
O
F
D
E
C
B
证明:
∵AC ∥DB
∴∠C=∠D,∠CAO=∠DBO
∴△CAO≌△DBO (AAS)
∵OA=OB
∴OC=OD
∵ E、F为OC、OD的中点
∴OE=OF
∴四边形AFBE为平行四边形(对角线互相平分的四边形是平行四边形)
例2、如图,在平行四边形ABCD中,E、F、G、H分别是各 边上的点,且AE=CF,BG=DH。求证:EF与GH互相平分。
例题讲解
证明:
分别连结HE、EG、GF、FD
∵四边形ABCD是平行四边形
∴AD=BC,∠A=∠C
∵BG=DH
∴AD-DH=BC-BG,
即: ADH=CG
∵AE=CF
∴△AEH≌△CFG(SAS)
∴EH=FG(全等三角形对应边相等)
同理可得△DFH≌△BEG(SAS)
∴HF=EG(全等三角形对应边相等)
∴四边形HEGF是平行四边形
∴EF与GH互相平分
2)已知有一条对角线被平分,再证另一条对角线被平分,构成判定定理3.
1)已知一组对角相等,再证另一组对角相等,构成判定定理2.
证一个四边形是平行四边形的思路:
先找现有条件
再证缺失条件
构成判定方法
平行四边形判定方法的选择方法
3)已知一组对边平行,可以证另一组对边平行,即定义法;也可证这组对边相等,构成判定定理4.
4)已知一组对边相等,可以证另一组对边相等,构成判定定理1;也可证这组对边平行,构成判定定理4.
新知总结
例3、已知:如图,□ABCD中,E、F分别是AC上两点,且BE⊥AC于E,DF⊥AC于F.
求证:四边形BEDF是平行四边形.
┓
┓
A
B
C
D
E
F
新知应用
方法一:
证明BE与DF平行且相等
证明:
∵四边形ABCD是平行四边形
∴AB=DC,且AB∥DC,
∴∠BAE=∠DCF
∵BE⊥AC于E,DF⊥AC于F
∴BE∥DF,∠AEB=∠CDF=90°
∴△ABE≌△CDF (AAS)
∴BE=DF
∴四边形BEDF是平行四边形
例3、已知:如图,□ABCD中,E、F分别是AC上两点,且BE⊥AC于E,DF⊥AC于F.
求证:四边形BEDF是平行四边形.
┓
┓
A
B
C
D
E
F
新知应用
方法二:
连结BD,证明BD与EF互相平分
证明:
∵四边形ABCD是平行四边形
∵∠BOE=∠DOF
∵BE⊥AC于E,DF⊥AC于F
∴∠AEB=∠CDF=90°
∴△BOE≌△DOF (AAS)
∴OE=OF
∴四边形BEDF是平行四边形
O
连结BD,交AC于O点
∴OD=OB,
例3、已知:如图,□ABCD中,E、F分别是AC上两点,且BE⊥AC于E,DF⊥AC于F.
求证:四边形BEDF是平行四边形.
┓
┓
A
B
C
D
E
F
新知应用
方法三:
利用面积法证明BE=DF,再根据BE∥DF得出结论
证明:
∵四边形ABCD是平行四边形
∵BE⊥AC于E,DF⊥AC于F
∴ BE∥DF ,∠AEB=∠CDF=90°
∴ BE=DF
∴四边形BEDF是平行四边形
∴S△ABC=S△CDA,
∴AC×BE= AC×DF,
你还能用其他方法证明吗?
变式1:
已知:平行四边形ABCD,对角线AC、BD相交于点O,E、F分别为OA、OC中点,求证:四边形BEDF是平行四边形。
证明:∵四边形ABCD是平行四边形
∴OA=OC,OB=OD(平行四边形的对角线互相平分)
∵E、F分别为OA、OC中点
∴OE=OA,,OF= OC
而OA=OC
∴OE=OF
又OB=OD
∴四边形BEDF是平行四边形
(对角线互相平分的四边形是 平行四边形)
C
A
D
B
E
F
O
你还有其他的证明方法吗?
新知应用
已知:平行四边形ABCD,对角线AC、BD相交于点O,AE=CF,求证:四边BEDF是平行四边形。
还可以是:①AF=CE
②∠ADE=∠CBF
③∠CDE=∠ABF
④BE⊥AC,DF⊥AC
……
若将“E、F分别为OA、OC中点”改为“AE=CF”,四边形BEDF还是平行四边形吗?
试试看:你还能怎样改?
A
D
B
C
O
E
F
BE∥DF
变式2:
新知应用
1、如图,AC∥ED,点B在AC上且AB=ED=BC 。找出图中的平行四边形。
A
C
B
E
D
课堂练习
□ABDE
□BCDE
一组对边平行且相等的四边形是平行四边形
(A)AB∥CD,AD∥BC
(B) AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠C
D
B
D
A
C
(两组对边分别平行)
(两组对边分别相等)
(一组对边平行且相等)
(两组对角分别相等或两组对边分别平行)
A
B
D
C
课堂练习
2、在下列条件中,不能判定四边形是平行四边形的是( )
1、在□ABCD中,E、F分别为AD、BC边上的一点,若再增加一个条件 ,就可推得BE = DF.
DE=BF
或BE∥DF
或AE=CF
提升练习
A
B
C
D
E
F
A
C
D
E
2.如图,E,F分别是 ABCD的两对边AD,BC的中点,则图中平行四边形的个数是( )
A.3个 B.4个 C.5个 D.6个
D
提升练习
B
F
A
C
D
E
3、在四边形ABCD中:①AB∥CD②AD∥BC③AB=CD④AD=BC,从以上选择两个条件使四边形ABCD为平行四边形的选法共有( )
A.3种 B.4种 C.5种 D.6种
B
提升练习
4、 ABCD中,E,F的对角线BD上不同的两点.下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AE=CF C.AF∥CE D.∠BAE=∠DCF
B
5、如图:□ABCD中, 以AD、BC为边作正三角形ADE, 正三角形BCF, 连结BE,DF, 求证: 四边形EBFD是平行四边形.
A
B
C
D
E
F
1
2
3
4
证明: 在 □ ABCD中,
AD = BC, AB = CD,∠1 = ∠2
∵△ADE与△BCF都是正三角形,
∴AE=DE=AD, BE=CF=BC,
∠3=∠4=60°.
∴DE=BF, AE=CF,
∠1+∠3=∠2+∠4,
即 ∠EAB=∠DCF,
∴△ABE≌△DCF
∴BE=DF
∴四边形EBFD是平行四边形.
提升练习
已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断:
①OA=OC,②AB=CD,③∠BAD=∠DCB,④AD∥BC.
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
①构造一个真命题,画图并给出证明;
②构造一个假命题,举反例加以说明.
提升拓展
∵AD∥BC,
∴∠DAC=∠BCA,∠ADB=∠DBC.
又∵OA=OC,
∴△AOD≌△COB.
∴AD=BC.
∴四边形ABCD为平行四边形.
(1)以①OA=OC、④AD∥BC论断为条件
解:
A
B
C
D
O
(2)②④论断为条件时,此时一组对边平行,另一组对边相等,可以构成等腰梯形.
A
B
D
C
提升拓展
从边来判定
1.两组对边分别平行的四边形是平行四边形(定义)
2.两组对边分别相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
平行四边形的判定方法总 结
3.一组对边平行且相等的四边形是平行四边形
课堂小结
19.2 平行四边形
第4课时 平行四边形的判定(二)
沪科版数学八年级下册
第19章 四边形
两组对边分别相等
两组对角分别相等
两组对边分别平行
一组对边平行且相等
四边形是平行四边形
从看边
从角看
已学的平行四边形的判定方法
知识回顾
四边形是平行四边形
对角线互相平分
从对角线看:
四边形是平行四边形
思 考
?
O
已知:四边形ABCD, 对角线AC、BD相交于点O,且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
证明:
在△AOD和△COB中
OA=OC(已知)
∠AOD=∠COB (对顶角相等)
OD=OB (已知)
∴△AOD≌△COB(SAS)
∴∠1=∠2 AD=CB(全等三角形的对应角、对应边相等)
∴ AD∥CB(内错角相等,两直线平行)
∴四边形ABCD是平行四边形
B
A
C
2
1
D
(一组对边平行且相等的四边形是平行四边形)
新知讲解
对角线互相平分的四边形是平行四边形
平行四边形的判定定理4:
符号语言:
A
B
C
D
O
∵ OA=OC,OB=OD
∴四边形ABCD是平行四边形
(对角线互相平分的四边形是平行四边形)
新知讲解
1.根据下列条件,不能判定一个四边形为平行四边形的是( )
(A)两组对边分别相等
(B)两条对角线互相平分
(C)两条对角线相等
(D)两组对边分别平行
C
新知辨析
2、请你识别下列四边形哪些是平行四边形 为什么?
A
D
C
B
110°
70°
110°
⑴
⑷
⑶
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
⑵
7.6㎝
7.6㎝
新知辨析
是平行四边形,对角线互相平分
是平行四边形,一组对边平行且相等
是平行四边形,两组对角分别相等
是平行四边形,两组对边分别相等
3、判断
(1)一组对边平行且另一组对边相等的四边形是 平行四边形; ( )
(2)两组对角都相等的四边形是平行四边形 ( )
(3)一组对边平行且一组对角相等的四边形是平行边形; ( )
(4)一组对边平行,一组邻角互补的四边形是平行 四边形; ( )
(5)两组邻角互补的四边形是平行四边形. ( )
×
√
√
×
×
新知辨析
例1、已知AB、CD交于O,AC ∥DB,OA=OB,E、F为OC、OD的中点,求证:四边形AFBE为平行四边形
例题讲解
A
O
F
D
E
C
B
证出OE=OF,
利用对角线互相平分得出结论
例1、已知AB、CD交于O,AC ∥DB,OA=OB,E、F为OC、OD的中点,求证:四边形AFBE为平行四边形
例题讲解
A
O
F
D
E
C
B
证明:
∵AC ∥DB
∴∠C=∠D,∠CAO=∠DBO
∴△CAO≌△DBO (AAS)
∵OA=OB
∴OC=OD
∵ E、F为OC、OD的中点
∴OE=OF
∴四边形AFBE为平行四边形(对角线互相平分的四边形是平行四边形)
例2、如图,在平行四边形ABCD中,E、F、G、H分别是各 边上的点,且AE=CF,BG=DH。求证:EF与GH互相平分。
例题讲解
证明:
分别连结HE、EG、GF、FD
∵四边形ABCD是平行四边形
∴AD=BC,∠A=∠C
∵BG=DH
∴AD-DH=BC-BG,
即: ADH=CG
∵AE=CF
∴△AEH≌△CFG(SAS)
∴EH=FG(全等三角形对应边相等)
同理可得△DFH≌△BEG(SAS)
∴HF=EG(全等三角形对应边相等)
∴四边形HEGF是平行四边形
∴EF与GH互相平分
2)已知有一条对角线被平分,再证另一条对角线被平分,构成判定定理3.
1)已知一组对角相等,再证另一组对角相等,构成判定定理2.
证一个四边形是平行四边形的思路:
先找现有条件
再证缺失条件
构成判定方法
平行四边形判定方法的选择方法
3)已知一组对边平行,可以证另一组对边平行,即定义法;也可证这组对边相等,构成判定定理4.
4)已知一组对边相等,可以证另一组对边相等,构成判定定理1;也可证这组对边平行,构成判定定理4.
新知总结
例3、已知:如图,□ABCD中,E、F分别是AC上两点,且BE⊥AC于E,DF⊥AC于F.
求证:四边形BEDF是平行四边形.
┓
┓
A
B
C
D
E
F
新知应用
方法一:
证明BE与DF平行且相等
证明:
∵四边形ABCD是平行四边形
∴AB=DC,且AB∥DC,
∴∠BAE=∠DCF
∵BE⊥AC于E,DF⊥AC于F
∴BE∥DF,∠AEB=∠CDF=90°
∴△ABE≌△CDF (AAS)
∴BE=DF
∴四边形BEDF是平行四边形
例3、已知:如图,□ABCD中,E、F分别是AC上两点,且BE⊥AC于E,DF⊥AC于F.
求证:四边形BEDF是平行四边形.
┓
┓
A
B
C
D
E
F
新知应用
方法二:
连结BD,证明BD与EF互相平分
证明:
∵四边形ABCD是平行四边形
∵∠BOE=∠DOF
∵BE⊥AC于E,DF⊥AC于F
∴∠AEB=∠CDF=90°
∴△BOE≌△DOF (AAS)
∴OE=OF
∴四边形BEDF是平行四边形
O
连结BD,交AC于O点
∴OD=OB,
例3、已知:如图,□ABCD中,E、F分别是AC上两点,且BE⊥AC于E,DF⊥AC于F.
求证:四边形BEDF是平行四边形.
┓
┓
A
B
C
D
E
F
新知应用
方法三:
利用面积法证明BE=DF,再根据BE∥DF得出结论
证明:
∵四边形ABCD是平行四边形
∵BE⊥AC于E,DF⊥AC于F
∴ BE∥DF ,∠AEB=∠CDF=90°
∴ BE=DF
∴四边形BEDF是平行四边形
∴S△ABC=S△CDA,
∴AC×BE= AC×DF,
你还能用其他方法证明吗?
变式1:
已知:平行四边形ABCD,对角线AC、BD相交于点O,E、F分别为OA、OC中点,求证:四边形BEDF是平行四边形。
证明:∵四边形ABCD是平行四边形
∴OA=OC,OB=OD(平行四边形的对角线互相平分)
∵E、F分别为OA、OC中点
∴OE=OA,,OF= OC
而OA=OC
∴OE=OF
又OB=OD
∴四边形BEDF是平行四边形
(对角线互相平分的四边形是 平行四边形)
C
A
D
B
E
F
O
你还有其他的证明方法吗?
新知应用
已知:平行四边形ABCD,对角线AC、BD相交于点O,AE=CF,求证:四边BEDF是平行四边形。
还可以是:①AF=CE
②∠ADE=∠CBF
③∠CDE=∠ABF
④BE⊥AC,DF⊥AC
……
若将“E、F分别为OA、OC中点”改为“AE=CF”,四边形BEDF还是平行四边形吗?
试试看:你还能怎样改?
A
D
B
C
O
E
F
BE∥DF
变式2:
新知应用
1、如图,AC∥ED,点B在AC上且AB=ED=BC 。找出图中的平行四边形。
A
C
B
E
D
课堂练习
□ABDE
□BCDE
一组对边平行且相等的四边形是平行四边形
(A)AB∥CD,AD∥BC
(B) AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠C
D
B
D
A
C
(两组对边分别平行)
(两组对边分别相等)
(一组对边平行且相等)
(两组对角分别相等或两组对边分别平行)
A
B
D
C
课堂练习
2、在下列条件中,不能判定四边形是平行四边形的是( )
1、在□ABCD中,E、F分别为AD、BC边上的一点,若再增加一个条件 ,就可推得BE = DF.
DE=BF
或BE∥DF
或AE=CF
提升练习
A
B
C
D
E
F
A
C
D
E
2.如图,E,F分别是 ABCD的两对边AD,BC的中点,则图中平行四边形的个数是( )
A.3个 B.4个 C.5个 D.6个
D
提升练习
B
F
A
C
D
E
3、在四边形ABCD中:①AB∥CD②AD∥BC③AB=CD④AD=BC,从以上选择两个条件使四边形ABCD为平行四边形的选法共有( )
A.3种 B.4种 C.5种 D.6种
B
提升练习
4、 ABCD中,E,F的对角线BD上不同的两点.下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AE=CF C.AF∥CE D.∠BAE=∠DCF
B
5、如图:□ABCD中, 以AD、BC为边作正三角形ADE, 正三角形BCF, 连结BE,DF, 求证: 四边形EBFD是平行四边形.
A
B
C
D
E
F
1
2
3
4
证明: 在 □ ABCD中,
AD = BC, AB = CD,∠1 = ∠2
∵△ADE与△BCF都是正三角形,
∴AE=DE=AD, BE=CF=BC,
∠3=∠4=60°.
∴DE=BF, AE=CF,
∠1+∠3=∠2+∠4,
即 ∠EAB=∠DCF,
∴△ABE≌△DCF
∴BE=DF
∴四边形EBFD是平行四边形.
提升练习
已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断:
①OA=OC,②AB=CD,③∠BAD=∠DCB,④AD∥BC.
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
①构造一个真命题,画图并给出证明;
②构造一个假命题,举反例加以说明.
提升拓展
∵AD∥BC,
∴∠DAC=∠BCA,∠ADB=∠DBC.
又∵OA=OC,
∴△AOD≌△COB.
∴AD=BC.
∴四边形ABCD为平行四边形.
(1)以①OA=OC、④AD∥BC论断为条件
解:
A
B
C
D
O
(2)②④论断为条件时,此时一组对边平行,另一组对边相等,可以构成等腰梯形.
A
B
D
C
提升拓展
从边来判定
1.两组对边分别平行的四边形是平行四边形(定义)
2.两组对边分别相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
平行四边形的判定方法总 结
3.一组对边平行且相等的四边形是平行四边形
课堂小结
