沪科版数学八年级下19.2平行四边形(第1课时平行四边形边、角性质)课件(共22张PPT)
文档属性
| 名称 | 沪科版数学八年级下19.2平行四边形(第1课时平行四边形边、角性质)课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 497.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
19.2 平行四边形
第1课时 平行四边形的边性质(一)
沪科版数学八年级下册
第19章 四边形
生活中常见各种各样的平行四边形
新知导入
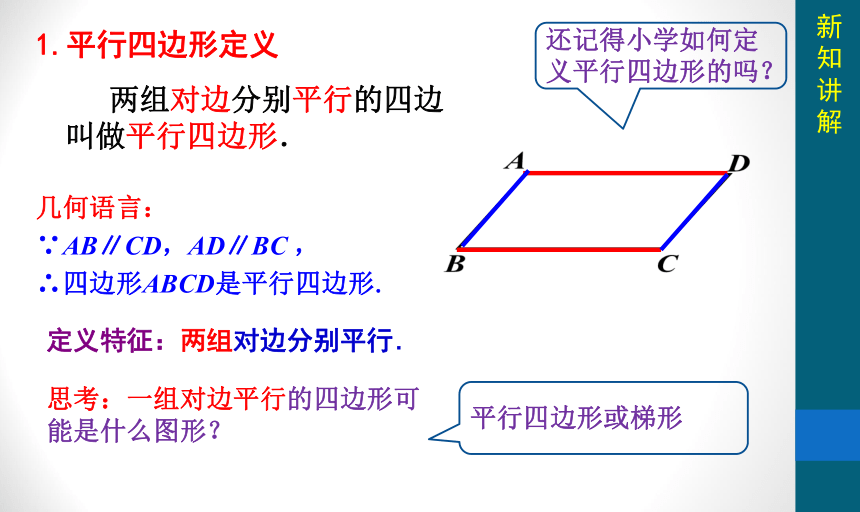
两组对边分别平行的四边叫做平行四边形.
几何语言:
∵AB∥CD,AD∥BC ,
∴四边形ABCD是平行四边形.
1.平行四边形定义
定义特征:两组对边分别平行.
新知讲解
还记得小学如何定义平行四边形的吗?
平行四边形或梯形
思考:一组对边平行的四边形可能是什么图形?
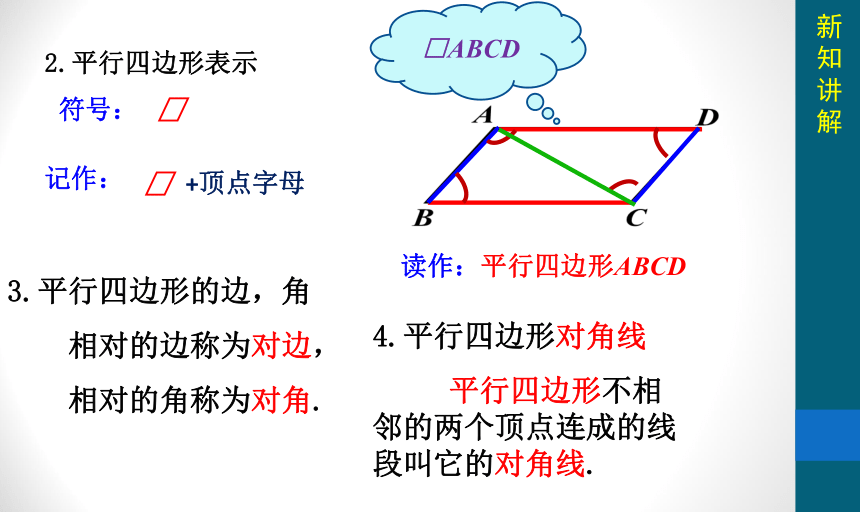
2.平行四边形表示
记作:
符号:
+顶点字母
读作:平行四边形ABCD
□ABCD
3.平行四边形的边,角
相对的边称为对边,
相对的角称为对角.
4.平行四边形对角线
平行四边形不相邻的两个顶点连成的线段叫它的对角线.
新知讲解
两组对边分别平行的四边形叫做平行四边形.
A
D
B
C
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
理解定义
ABCD
AB
CD
AD
BC
①
②
ABCD
AB
CD
AD
BC
新知讲解
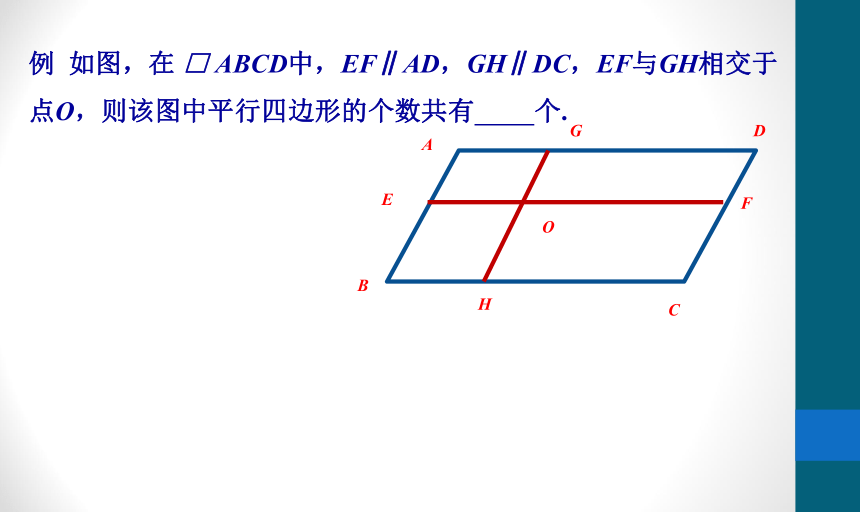
例 如图,在 □ ABCD中,EF∥AD,GH∥DC,EF与GH相交于点O,则该图中平行四边形的个数共有 个.
A
B
C
D
O
G
H
F
E
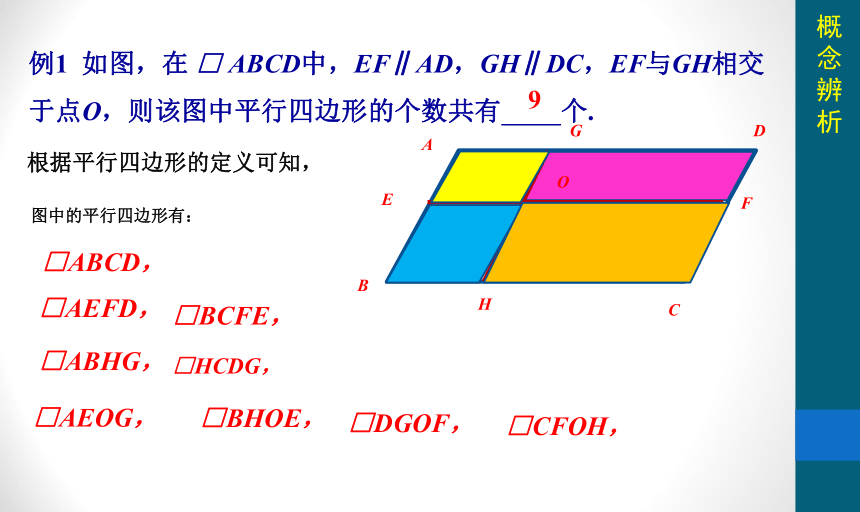
例1 如图,在 □ ABCD中,EF∥AD,GH∥DC,EF与GH相交于点O,则该图中平行四边形的个数共有 个.
A
B
C
D
O
G
H
F
E
□ABCD,
根据平行四边形的定义可知,
图中的平行四边形有:
□AEFD,
□BCFE,
□ABHG,
□HCDG,
□AEOG,
□BHOE,
□DGOF,
□CFOH,
9
概念辨析
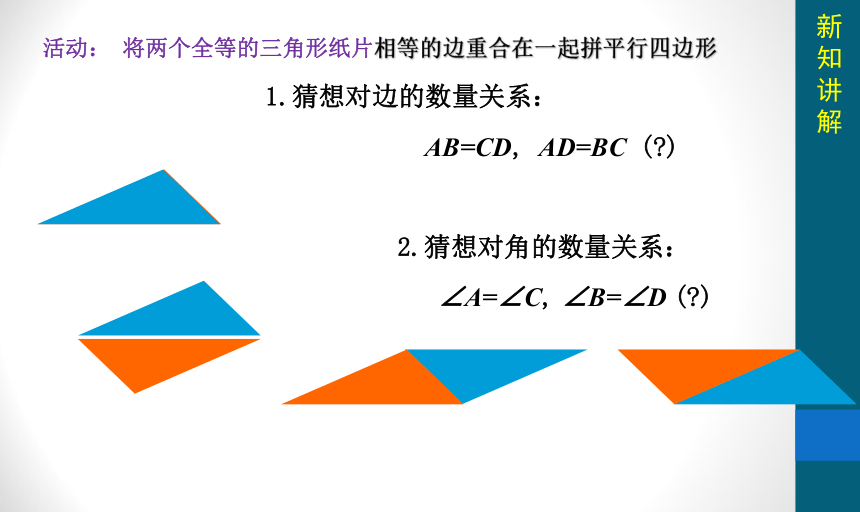
活动: 将两个全等的三角形纸片相等的边重合在一起拼平行四边形
1.猜想对边的数量关系:
AB=CD, AD=BC ( )
2.猜想对角的数量关系:
∠A=∠C, ∠B=∠D ( )
新知讲解
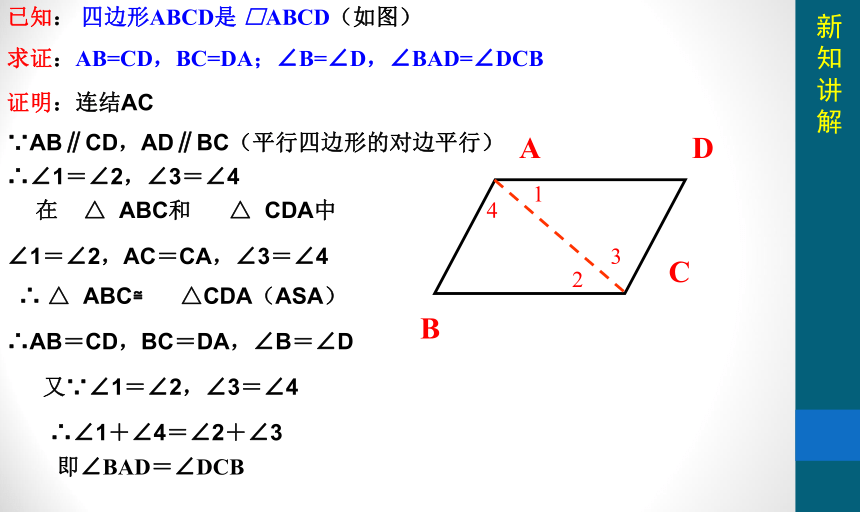
已知: 四边形ABCD是 □ABCD(如图)
求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB
即∠BAD=∠DCB
证明:连结AC
∵AB∥CD,AD∥BC(平行四边形的对边平行)
∴∠1=∠2,∠3=∠4
∠1=∠2,AC=CA,∠3=∠4
∴ △ ABC≌ △CDA(ASA)
∴AB=CD,BC=DA,∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在 △ ABC和 △ CDA中
A
B
C
D
1
2
3
4
新知讲解
平行四边形的性质
几何语言:
定理1:平行四边形的两组对边分别相等
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
∴ ∠A= ∠C, ∠B= ∠D(平行四边形的对角相等)
定理2:平行四边形的两组对角分别相等
∵ 四边形ABCD是平行四边形
注意:∴ ∠A+∠B=180°,∠B+∠C=180°
平行四边形的邻角互补
新知讲解
解:
∵四边形ABCD是平行四边形
且∠A=52°(已知)
∴ ∠A=∠C=52°(平行四边形的对角相等)
又∵AD∥BC(平行四边形的对边平行)
∴∠A+∠B=180°(两直线平行,同旁内角互补)
∴∠B=∠D= 180 °-∠A= 180 - 52°=128 °
例1、在□ABCD中,已知∠A=52 ° ,求其余三个角的度数。
A
B
C
D
52°
新知应用
解:∵四边形ABCD是平行四边形(已知)
∴ AB=CD,BC=AD(平行四边形的对边相等)
又∵□ABCD的周长为60cm.
∴AB + BC=30cm.
又AB:BC=3:2,即AB=1.5BC.
则 1.5BC + BC=30 , 解得 BC=12 (cm).
而 AB=1.5×12=18 (cm).
A
B
D
C
例2、已知平行四边形 ABCD的周长为60cm,两邻边AB,BC长的比为3:2,求AB和BC的长度 .
新知应用
讨论:
如图,直线l1 ∥l2 ,AB,CD是夹在l1 与l2间的两条平行线段,请问: AB与CD 相等吗?为什么?
l1
l2
A
B
C
D
AB=CD
∵l1 ∥l2 , AB∥CD
∴ ABCD是平行四边形
∴AB=CD
新知探究
若EF∥AB,那么EF、AB、CD相等吗?
讨论:
如图,直线l1 ∥l2 ,AB,CD是夹在l1 与l2间的两条平行线段,请问: AB与CD 相等吗?
l1
l2
A
B
C
D
你能总结这个现象吗?
E
F
EF=AB=CD
结论:
夹在两条平行线之间的平行线段相等
新知探究
讨论:
如图,直线l1 ∥l2 ,AB⊥l1 ,CD⊥l2,垂足分别为B、D,请问: AB与CD 相等吗?
l1
l2
A
B
C
D
线段AB的长就是平行线间的距离
┓
┓
AB=CD
平行线之间的距离
平行线之间的距离处处相等
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
结论:
新知探究
两条平行线之间的距离与点和点之间的距离、点到线之间的距离有何区别与联系?
a
b
A
B
∟
答:
点到直线的距离只有一条,即过直线外点作直线的垂线段的长度;
平行线的距离有无数条即一直线任一点都可以得到一条两平行直线的距离.
∟
讨论:
A
B
一点到另一条直线的距离
平行线之间的距离
新知探究
例 3、 如图,直线AE//BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为 .
A
B
C
D
E
解
设高为h,
S△ABD= ·BD·h=16,
∴h=4,
∴ S △ACE = ×5 ×4=10.
10
平行线之间的距离处处相等
新知应用
变式练习
变式:
在□ABCD中,∠A=150°,AB=8cm,BC=10cm,
(1)则S □ABCD= .
过点A作AE⊥BC于E,然后利用勾股定理求出AE的值.
40cm2
(2)若点P是□ABCD上AD上任意一点,那么△PBC的面积是 .
20cm2
△PBC与□ABCD是同底等高.
A
B
D
C
∟
E
A
B
D
C
P
S△PBC= S□ABCD=20(cm )
1.已知□ ABCD中,∠1=60°,则:
∠A= ,∠B= , ∠C= ,∠D= .
2、在□ ABCD 中,∠ADC=120°, ∠CAD=20°,则
∠ABC= , ∠CAB= .
A
B
C
D
(1小题)
(2小题)
60 °
120 °
60 °
120 °
120 °
40 °
A
B
C
D
1
课堂练习
2、 已知如图:E、F是平行四边形ABCD的对角线 AC上的两点,AE=CF
求证:(1)△ADF≌ △CBE (2)EB∥DF
1
2
3
4
证明:(1)
∵平行四边形ABCD中,AD∥CB
∴AD=CB,∠1=∠2
∵ AE=CF ∴ AE+EF=CF+EF,即AF=CE
∴△AFD≌△CEB(SAS)
(2) ∵△AFD≌△CEB
∴∠3=∠4
∴ DF∥EB
课堂练习
在△ABC中,AD平分∠BAC,点M,E,F分别是AB,AD,AC上的点,四边形BEFM是平行四边形。
求证:AF=BM
B
D
C
E
F
A
M
证明:
∵ 四边形BEFM是平行四边形
∴BM=EF AB//EF
∵ AD平分∠BAC
∴∠BAD=∠CAD
∵AB//EF
∴ ∠BAD=∠AEF
∴∠CAD =∠AEF
∴ AF=EF
∴ AF=BM
提升练习
1、两组对边分别平行的四边形叫做平行四边形.
2、平行四边形的性质:对边平行
对边相等
对角相等
邻角互补
3、 夹在两条平行线间的距离处处相等
课堂小结
19.2 平行四边形
第1课时 平行四边形的边性质(一)
沪科版数学八年级下册
第19章 四边形
生活中常见各种各样的平行四边形
新知导入
两组对边分别平行的四边叫做平行四边形.
几何语言:
∵AB∥CD,AD∥BC ,
∴四边形ABCD是平行四边形.
1.平行四边形定义
定义特征:两组对边分别平行.
新知讲解
还记得小学如何定义平行四边形的吗?
平行四边形或梯形
思考:一组对边平行的四边形可能是什么图形?
2.平行四边形表示
记作:
符号:
+顶点字母
读作:平行四边形ABCD
□ABCD
3.平行四边形的边,角
相对的边称为对边,
相对的角称为对角.
4.平行四边形对角线
平行四边形不相邻的两个顶点连成的线段叫它的对角线.
新知讲解
两组对边分别平行的四边形叫做平行四边形.
A
D
B
C
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
理解定义
ABCD
AB
CD
AD
BC
①
②
ABCD
AB
CD
AD
BC
新知讲解
例 如图,在 □ ABCD中,EF∥AD,GH∥DC,EF与GH相交于点O,则该图中平行四边形的个数共有 个.
A
B
C
D
O
G
H
F
E
例1 如图,在 □ ABCD中,EF∥AD,GH∥DC,EF与GH相交于点O,则该图中平行四边形的个数共有 个.
A
B
C
D
O
G
H
F
E
□ABCD,
根据平行四边形的定义可知,
图中的平行四边形有:
□AEFD,
□BCFE,
□ABHG,
□HCDG,
□AEOG,
□BHOE,
□DGOF,
□CFOH,
9
概念辨析
活动: 将两个全等的三角形纸片相等的边重合在一起拼平行四边形
1.猜想对边的数量关系:
AB=CD, AD=BC ( )
2.猜想对角的数量关系:
∠A=∠C, ∠B=∠D ( )
新知讲解
已知: 四边形ABCD是 □ABCD(如图)
求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB
即∠BAD=∠DCB
证明:连结AC
∵AB∥CD,AD∥BC(平行四边形的对边平行)
∴∠1=∠2,∠3=∠4
∠1=∠2,AC=CA,∠3=∠4
∴ △ ABC≌ △CDA(ASA)
∴AB=CD,BC=DA,∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在 △ ABC和 △ CDA中
A
B
C
D
1
2
3
4
新知讲解
平行四边形的性质
几何语言:
定理1:平行四边形的两组对边分别相等
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
∴ ∠A= ∠C, ∠B= ∠D(平行四边形的对角相等)
定理2:平行四边形的两组对角分别相等
∵ 四边形ABCD是平行四边形
注意:∴ ∠A+∠B=180°,∠B+∠C=180°
平行四边形的邻角互补
新知讲解
解:
∵四边形ABCD是平行四边形
且∠A=52°(已知)
∴ ∠A=∠C=52°(平行四边形的对角相等)
又∵AD∥BC(平行四边形的对边平行)
∴∠A+∠B=180°(两直线平行,同旁内角互补)
∴∠B=∠D= 180 °-∠A= 180 - 52°=128 °
例1、在□ABCD中,已知∠A=52 ° ,求其余三个角的度数。
A
B
C
D
52°
新知应用
解:∵四边形ABCD是平行四边形(已知)
∴ AB=CD,BC=AD(平行四边形的对边相等)
又∵□ABCD的周长为60cm.
∴AB + BC=30cm.
又AB:BC=3:2,即AB=1.5BC.
则 1.5BC + BC=30 , 解得 BC=12 (cm).
而 AB=1.5×12=18 (cm).
A
B
D
C
例2、已知平行四边形 ABCD的周长为60cm,两邻边AB,BC长的比为3:2,求AB和BC的长度 .
新知应用
讨论:
如图,直线l1 ∥l2 ,AB,CD是夹在l1 与l2间的两条平行线段,请问: AB与CD 相等吗?为什么?
l1
l2
A
B
C
D
AB=CD
∵l1 ∥l2 , AB∥CD
∴ ABCD是平行四边形
∴AB=CD
新知探究
若EF∥AB,那么EF、AB、CD相等吗?
讨论:
如图,直线l1 ∥l2 ,AB,CD是夹在l1 与l2间的两条平行线段,请问: AB与CD 相等吗?
l1
l2
A
B
C
D
你能总结这个现象吗?
E
F
EF=AB=CD
结论:
夹在两条平行线之间的平行线段相等
新知探究
讨论:
如图,直线l1 ∥l2 ,AB⊥l1 ,CD⊥l2,垂足分别为B、D,请问: AB与CD 相等吗?
l1
l2
A
B
C
D
线段AB的长就是平行线间的距离
┓
┓
AB=CD
平行线之间的距离
平行线之间的距离处处相等
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
结论:
新知探究
两条平行线之间的距离与点和点之间的距离、点到线之间的距离有何区别与联系?
a
b
A
B
∟
答:
点到直线的距离只有一条,即过直线外点作直线的垂线段的长度;
平行线的距离有无数条即一直线任一点都可以得到一条两平行直线的距离.
∟
讨论:
A
B
一点到另一条直线的距离
平行线之间的距离
新知探究
例 3、 如图,直线AE//BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为 .
A
B
C
D
E
解
设高为h,
S△ABD= ·BD·h=16,
∴h=4,
∴ S △ACE = ×5 ×4=10.
10
平行线之间的距离处处相等
新知应用
变式练习
变式:
在□ABCD中,∠A=150°,AB=8cm,BC=10cm,
(1)则S □ABCD= .
过点A作AE⊥BC于E,然后利用勾股定理求出AE的值.
40cm2
(2)若点P是□ABCD上AD上任意一点,那么△PBC的面积是 .
20cm2
△PBC与□ABCD是同底等高.
A
B
D
C
∟
E
A
B
D
C
P
S△PBC= S□ABCD=20(cm )
1.已知□ ABCD中,∠1=60°,则:
∠A= ,∠B= , ∠C= ,∠D= .
2、在□ ABCD 中,∠ADC=120°, ∠CAD=20°,则
∠ABC= , ∠CAB= .
A
B
C
D
(1小题)
(2小题)
60 °
120 °
60 °
120 °
120 °
40 °
A
B
C
D
1
课堂练习
2、 已知如图:E、F是平行四边形ABCD的对角线 AC上的两点,AE=CF
求证:(1)△ADF≌ △CBE (2)EB∥DF
1
2
3
4
证明:(1)
∵平行四边形ABCD中,AD∥CB
∴AD=CB,∠1=∠2
∵ AE=CF ∴ AE+EF=CF+EF,即AF=CE
∴△AFD≌△CEB(SAS)
(2) ∵△AFD≌△CEB
∴∠3=∠4
∴ DF∥EB
课堂练习
在△ABC中,AD平分∠BAC,点M,E,F分别是AB,AD,AC上的点,四边形BEFM是平行四边形。
求证:AF=BM
B
D
C
E
F
A
M
证明:
∵ 四边形BEFM是平行四边形
∴BM=EF AB//EF
∵ AD平分∠BAC
∴∠BAD=∠CAD
∵AB//EF
∴ ∠BAD=∠AEF
∴∠CAD =∠AEF
∴ AF=EF
∴ AF=BM
提升练习
1、两组对边分别平行的四边形叫做平行四边形.
2、平行四边形的性质:对边平行
对边相等
对角相等
邻角互补
3、 夹在两条平行线间的距离处处相等
课堂小结
