沪科版数学八年级下19.2平行四边形 第3课时平行四边形判定(一) (共21张PPT)
文档属性
| 名称 | 沪科版数学八年级下19.2平行四边形 第3课时平行四边形判定(一) (共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 257.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 09:32:16 | ||
图片预览



文档简介
(共21张PPT)
19.2 平行四边形
第3课时 平行四边形的判定(一)
沪科版数学八年级下册
第19章 四边形
两组对边分别平行的四边形叫做平行四 边形
平行四边形的对边相等;
平行四边形的对角相等.
平行四边形的对角线互相平分.
平行四边形性质:
平行四边形定义:
知识回顾
研究对象 研究结果 几何表示
对边
对角
邻角
对角线
平行且相等
AB∥CD,AD∥BC
=
=
∠A=∠C,∠B=∠D
∠A+∠B=180°
AO=CO BO=DO
相等
互补
互相平分
O
B
A
C
D
定义既是平行四边形的性质也可以是平行四边形的判定的依据
说一说平行四边形性质的逆命题
讨论:
类型 平行四边形性质 平行四边形性质
的逆命题
对边
对角
对角线
平行四边形的对边相等
平行四边形的对边平行
2、两组对边分别相等的四边形是平行四边形
1、一组对边平行且相等的四边形是平行四边形
平行四边形的对角相等
3、两组对角分别相等的四边形是平行四边形
4、对角线互相平分的四边形是平行四边形
平行四边形的对角线
互相平分
这些逆命题成立吗
新知探究
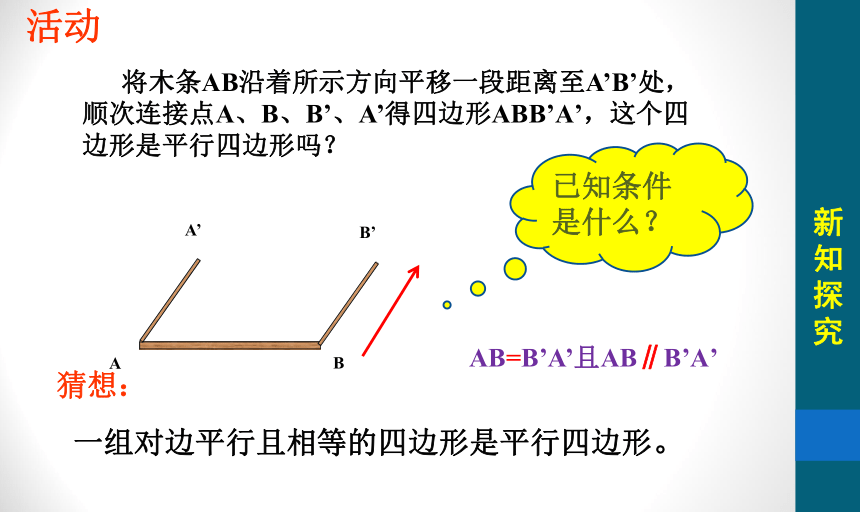
活动
将木条AB沿着所示方向平移一段距离至A’B’处,顺次连接点A、B、B’、A’得四边形ABB’A’,这个四边形是平行四边形吗?
A
B
B’
A’
已知条件是什么?
AB=B’A’且AB∥B’A’
猜想:
一组对边平行且相等的四边形是平行四边形。
新知探究
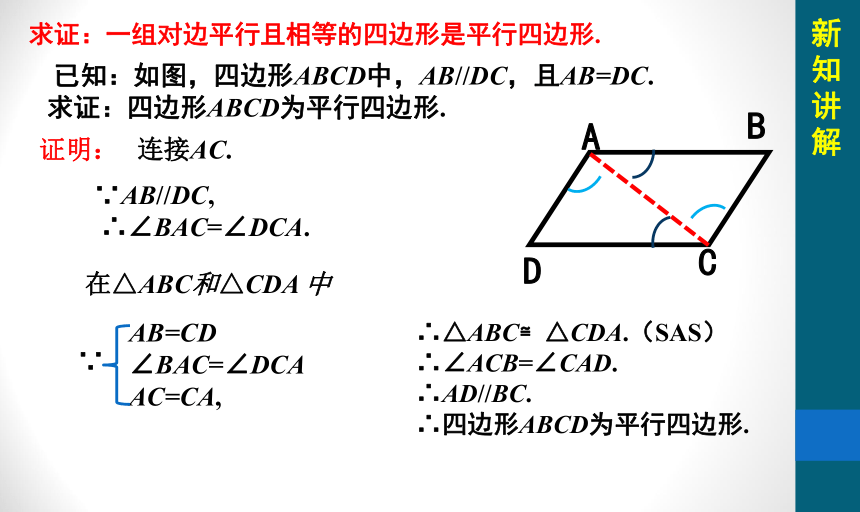
已知:如图,四边形ABCD中,AB//DC,且AB=DC.
求证:四边形ABCD为平行四边形.
∴△ABC≌△CDA.(SAS)
∴∠ACB=∠CAD.
∴AD//BC.
∴四边形ABCD为平行四边形.
求证:一组对边平行且相等的四边形是平行四边形.
新知讲解
A
C
D
B
证明:
连接AC.
∵AB//DC,
∴∠BAC=∠DCA.
在△ABC和△CDA 中
AB=CD
∠BAC=∠DCA
AC=CA,
∵
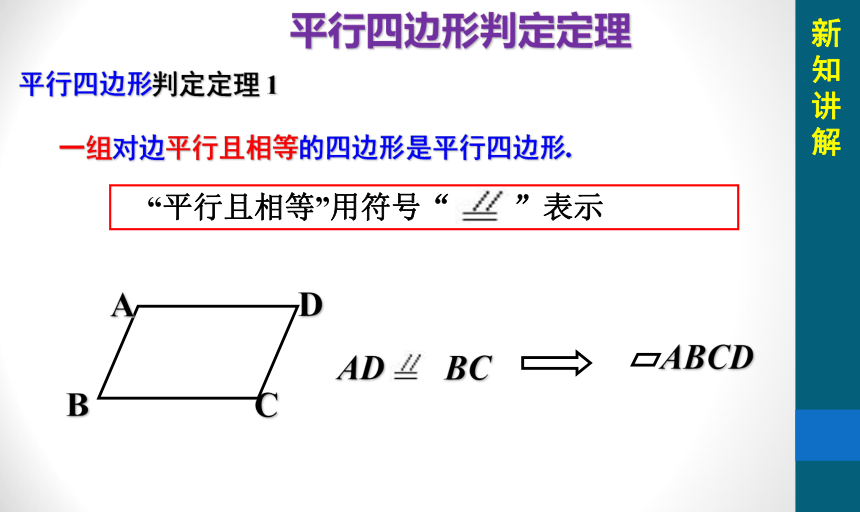
平行四边形判定定理 1
一组对边平行且相等的四边形是平行四边形.
A
B
C
D
ABCD
“平行且相等”用符号“ ”表示
AD BC
平行四边形判定定理
新知讲解
A
B
C
D
E
F
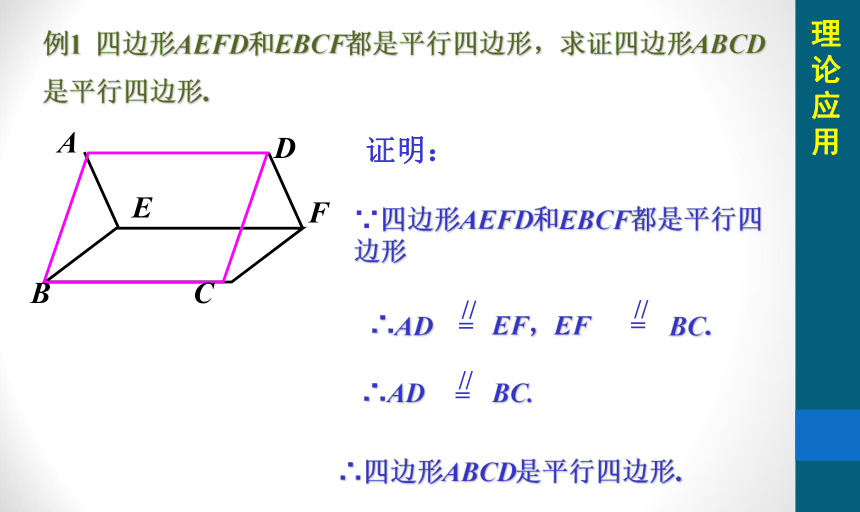
∴AD EF,EF BC.
//
=
//
=
∴AD BC.
//
=
例1 四边形AEFD和EBCF都是平行四边形,求证四边形ABCD 是平行四边形.
理论应用
证明:
∵四边形AEFD和EBCF都是平行四边形
∴四边形ABCD是平行四边形.
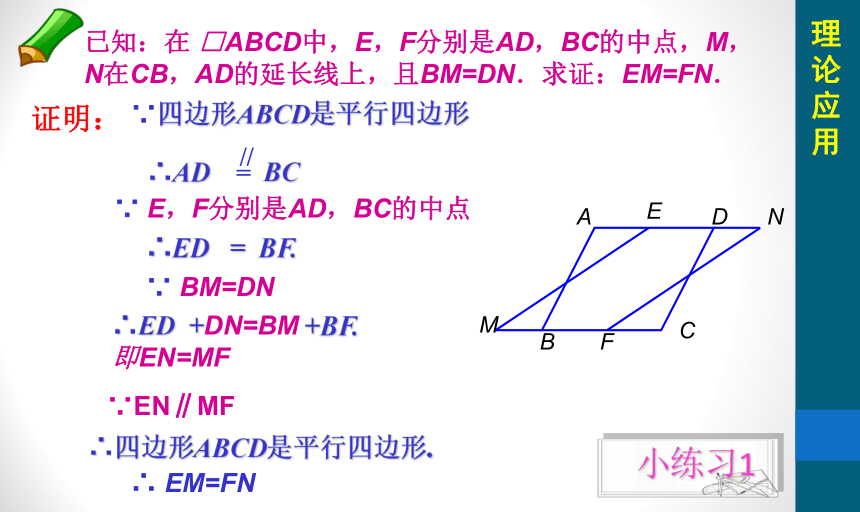
已知:在 □ABCD中,E,F分别是AD,BC的中点,M,N在CB,AD的延长线上,且BM=DN.求证:EM=FN.
E
M
D
N
F
C
A
B
小练习1
理论应用
∴AD BC
//
=
∴ED = BF.
证明:
∵四边形ABCD是平行四边形
∴四边形ABCD是平行四边形.
∵ E,F分别是AD,BC的中点
∵ BM=DN
∴ED +DN=BM +BF.
即EN=MF
∵EN∥MF
∴ EM=FN
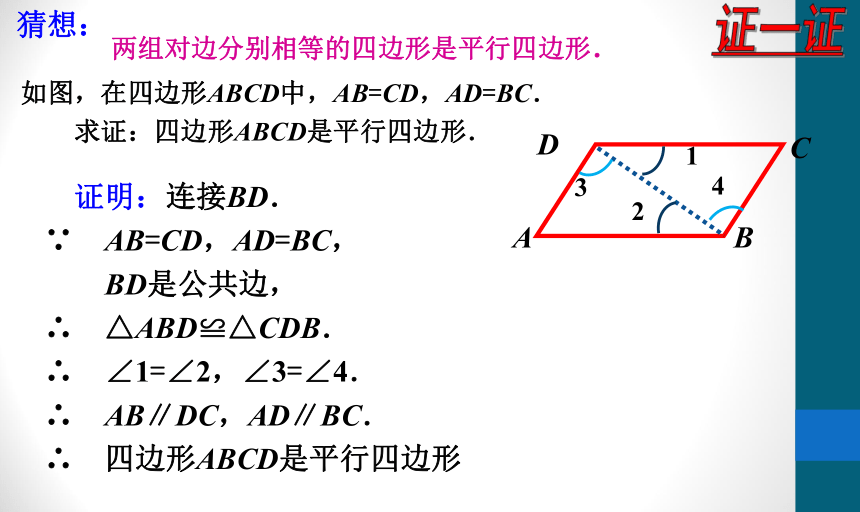
证明:连接BD.
∵ AB=CD,AD=BC,
BD是公共边,
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形
如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
猜想:
D
A
B
C
证一证
1
2
3
4
平行四边形判定定理 2
两组对边分别相等的四边形是平行四边形
平行四边形判定定理
A
B
C
D
∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
几何语言:
新知讲解
D
A
B
C
E
F
证明:
∵四边形ABCD是平行四边形
AD ∥ BC且AD =BC
∴∠EAD= ∠FCB
△AED ≌ △ CFB(SAS)
DE=BF
∴四边形BFDE是平行四边形
在 △ AED和 △ CFB中
同理可证:BE=DF
例2:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。求证:四边形BFDE是平行四边形
理论应用
AE=CF
∠EAD= ∠FCB
AD=BC
∵
A
B
C
D
又∵∠A=∠C,∠B=∠D
证明:∵∠A+∠C+∠B+∠D=3600
∴2∠A+2∠B=3600
即∠A+∠B=1800
∴ AD∥ BC
∴四边形ABCD是平行四边形.
∴AB∥ CD
判定定理3:两组对角分别相等的四边形是平行四边形.
例3、已知四边形ABCD中,∠A=∠C,∠B=∠D,求证:四边 形ABCD是平行四边形.
例题讲解
同理得 ∠C+∠B=1800
若一组对边平行,另一组对边相等,这个四边形是平行四边形吗?
1、在下列条件中,能判定四边形ABCD为平行四边形的是( )
A.AB=AD,CB=CD
B.AB∥CD,AD=BC
D.∠A=∠B,∠C=∠D
C.AD=BC,AB=CD
A
B
C
D
C
理论应用
小练习2
2、下面给出了四边形ABCD中 ∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的 是( )
A.1:2:3:4
C.2:3:2:3
B.2:2:3:3
需要两组对角分别相等
D.2:3:3:2
C
小练习2
理论应用
3、如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于点F,AB=BF.添加一个条件使四边形ABCD是平行四边形,你认为下面四个条件中可选择的是( )
A.AD=BC B.CD=BFC.∠A=∠C D.∠F=∠CDF
小练习2
理论应用
A
B
C
D
E
F
D
∵E是BC边的中点,
∴CE=BE.
又∵∠DEC=∠FEB,
添加∠F=∠CDE
∴△DCE≌△FBE(AAS)
∴CD=BF.
又∵∠F=∠CDE,
∴CD∥BF,即CD∥AB.
又已知AB=BF,
∴CD=AB,
∴四边形ABCD是平行四边形.
理由如下:
4、填空题: 如图,在四边形ABCD中,
①如果AD=8cm,AB=4cm,且BC=____cm,CD=____cm,那么四边形ABCD是平行四边形。
8
4
两组对边分别相等的四边形是平行四边形
A
B
C
D
理论应用
小练习2
②若∠A=1200,则∠B=____0,∠C=____0,∠D=____0时,四边形ABCD是平行四边形。
120
60
60
两组对角分别相等的四边形是平行四边形
③如果AD//BC,AD=6cm,且BC=___cm,那么四边形ABCD是平行四边形。
6
一组对边平行且相等的四边形是平行四边形
A
B
C
D
1、已知:如图,□ABCD中,E、F分别是AC上两点,且BE⊥AC于E,DF⊥AC于F.求证:四边形BEDF是平行四边形.
┓
┓
A
B
C
D
E
F
提升练习
证明:∵ 四边形ABCD是平行四边形,
∴ AB=CD,且AB∥CD.
∴ ∠BAE=∠DCF.
∵ BE⊥AC于E,DF⊥AC于F,
∴ BE∥DF,且∠BEA=∠DFC=90°.
∴ △ABE≌△CDF (AAS).
∴ BE=DF.
∴ 四边形BEDF是平行四边形(一组对边平行且相等的四边形平行四边形).
2、有一块平行四边形的玻璃块,假如不小心碰碎了一部分,聪明的技师拿着细绳很快将原来的平行四边形画了出来,你知道他用的是什么方法吗?
A
C
B
提升练习
D
c
b
a
A’
C’
B’
a
c
b
设AB=a,BC=b,A C=c
(1)作△A’B’C’,使得A’B’=a,B’C’=b,A’ C’=c
(2)用圆规以A’为圆心,b为半径画弧,再以C’为圆心a为半径画弧,两弧交点为D,
(3)连接A’D,C’D,即可得□A’B’C’D.
两组对边分别相等的四边形为平行四边形
a
b
任选教室里不坐在同一直线上的三个同学作为一个平行四边形的三个顶点,那么第四个顶点是哪个座位的同学,请你站起来。
A
B
C
以三角形任两边为邻边作平行四边形可作3个。
A
D
B
C
D
A
B
C
A
B
C
D
提升练习
变式:
A
B
C
D
AB=DC AD=BC
AB∥DC AD∥BC
ABCD
∠ABC=∠ADC ∠BAD=∠BCD
判定一:
一组对边平行且相等的四边形是平行四边形
ABCD
ABCD
课堂小结
本节课学习了几个平行四边形判定方法?
判定二:
两组对边分部相等的四边形是平行四边形
判定三:
两组对角分部相等的四边形是平行四边形
19.2 平行四边形
第3课时 平行四边形的判定(一)
沪科版数学八年级下册
第19章 四边形
两组对边分别平行的四边形叫做平行四 边形
平行四边形的对边相等;
平行四边形的对角相等.
平行四边形的对角线互相平分.
平行四边形性质:
平行四边形定义:
知识回顾
研究对象 研究结果 几何表示
对边
对角
邻角
对角线
平行且相等
AB∥CD,AD∥BC
=
=
∠A=∠C,∠B=∠D
∠A+∠B=180°
AO=CO BO=DO
相等
互补
互相平分
O
B
A
C
D
定义既是平行四边形的性质也可以是平行四边形的判定的依据
说一说平行四边形性质的逆命题
讨论:
类型 平行四边形性质 平行四边形性质
的逆命题
对边
对角
对角线
平行四边形的对边相等
平行四边形的对边平行
2、两组对边分别相等的四边形是平行四边形
1、一组对边平行且相等的四边形是平行四边形
平行四边形的对角相等
3、两组对角分别相等的四边形是平行四边形
4、对角线互相平分的四边形是平行四边形
平行四边形的对角线
互相平分
这些逆命题成立吗
新知探究
活动
将木条AB沿着所示方向平移一段距离至A’B’处,顺次连接点A、B、B’、A’得四边形ABB’A’,这个四边形是平行四边形吗?
A
B
B’
A’
已知条件是什么?
AB=B’A’且AB∥B’A’
猜想:
一组对边平行且相等的四边形是平行四边形。
新知探究
已知:如图,四边形ABCD中,AB//DC,且AB=DC.
求证:四边形ABCD为平行四边形.
∴△ABC≌△CDA.(SAS)
∴∠ACB=∠CAD.
∴AD//BC.
∴四边形ABCD为平行四边形.
求证:一组对边平行且相等的四边形是平行四边形.
新知讲解
A
C
D
B
证明:
连接AC.
∵AB//DC,
∴∠BAC=∠DCA.
在△ABC和△CDA 中
AB=CD
∠BAC=∠DCA
AC=CA,
∵
平行四边形判定定理 1
一组对边平行且相等的四边形是平行四边形.
A
B
C
D
ABCD
“平行且相等”用符号“ ”表示
AD BC
平行四边形判定定理
新知讲解
A
B
C
D
E
F
∴AD EF,EF BC.
//
=
//
=
∴AD BC.
//
=
例1 四边形AEFD和EBCF都是平行四边形,求证四边形ABCD 是平行四边形.
理论应用
证明:
∵四边形AEFD和EBCF都是平行四边形
∴四边形ABCD是平行四边形.
已知:在 □ABCD中,E,F分别是AD,BC的中点,M,N在CB,AD的延长线上,且BM=DN.求证:EM=FN.
E
M
D
N
F
C
A
B
小练习1
理论应用
∴AD BC
//
=
∴ED = BF.
证明:
∵四边形ABCD是平行四边形
∴四边形ABCD是平行四边形.
∵ E,F分别是AD,BC的中点
∵ BM=DN
∴ED +DN=BM +BF.
即EN=MF
∵EN∥MF
∴ EM=FN
证明:连接BD.
∵ AB=CD,AD=BC,
BD是公共边,
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形
如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
猜想:
D
A
B
C
证一证
1
2
3
4
平行四边形判定定理 2
两组对边分别相等的四边形是平行四边形
平行四边形判定定理
A
B
C
D
∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
几何语言:
新知讲解
D
A
B
C
E
F
证明:
∵四边形ABCD是平行四边形
AD ∥ BC且AD =BC
∴∠EAD= ∠FCB
△AED ≌ △ CFB(SAS)
DE=BF
∴四边形BFDE是平行四边形
在 △ AED和 △ CFB中
同理可证:BE=DF
例2:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。求证:四边形BFDE是平行四边形
理论应用
AE=CF
∠EAD= ∠FCB
AD=BC
∵
A
B
C
D
又∵∠A=∠C,∠B=∠D
证明:∵∠A+∠C+∠B+∠D=3600
∴2∠A+2∠B=3600
即∠A+∠B=1800
∴ AD∥ BC
∴四边形ABCD是平行四边形.
∴AB∥ CD
判定定理3:两组对角分别相等的四边形是平行四边形.
例3、已知四边形ABCD中,∠A=∠C,∠B=∠D,求证:四边 形ABCD是平行四边形.
例题讲解
同理得 ∠C+∠B=1800
若一组对边平行,另一组对边相等,这个四边形是平行四边形吗?
1、在下列条件中,能判定四边形ABCD为平行四边形的是( )
A.AB=AD,CB=CD
B.AB∥CD,AD=BC
D.∠A=∠B,∠C=∠D
C.AD=BC,AB=CD
A
B
C
D
C
理论应用
小练习2
2、下面给出了四边形ABCD中 ∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的 是( )
A.1:2:3:4
C.2:3:2:3
B.2:2:3:3
需要两组对角分别相等
D.2:3:3:2
C
小练习2
理论应用
3、如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于点F,AB=BF.添加一个条件使四边形ABCD是平行四边形,你认为下面四个条件中可选择的是( )
A.AD=BC B.CD=BFC.∠A=∠C D.∠F=∠CDF
小练习2
理论应用
A
B
C
D
E
F
D
∵E是BC边的中点,
∴CE=BE.
又∵∠DEC=∠FEB,
添加∠F=∠CDE
∴△DCE≌△FBE(AAS)
∴CD=BF.
又∵∠F=∠CDE,
∴CD∥BF,即CD∥AB.
又已知AB=BF,
∴CD=AB,
∴四边形ABCD是平行四边形.
理由如下:
4、填空题: 如图,在四边形ABCD中,
①如果AD=8cm,AB=4cm,且BC=____cm,CD=____cm,那么四边形ABCD是平行四边形。
8
4
两组对边分别相等的四边形是平行四边形
A
B
C
D
理论应用
小练习2
②若∠A=1200,则∠B=____0,∠C=____0,∠D=____0时,四边形ABCD是平行四边形。
120
60
60
两组对角分别相等的四边形是平行四边形
③如果AD//BC,AD=6cm,且BC=___cm,那么四边形ABCD是平行四边形。
6
一组对边平行且相等的四边形是平行四边形
A
B
C
D
1、已知:如图,□ABCD中,E、F分别是AC上两点,且BE⊥AC于E,DF⊥AC于F.求证:四边形BEDF是平行四边形.
┓
┓
A
B
C
D
E
F
提升练习
证明:∵ 四边形ABCD是平行四边形,
∴ AB=CD,且AB∥CD.
∴ ∠BAE=∠DCF.
∵ BE⊥AC于E,DF⊥AC于F,
∴ BE∥DF,且∠BEA=∠DFC=90°.
∴ △ABE≌△CDF (AAS).
∴ BE=DF.
∴ 四边形BEDF是平行四边形(一组对边平行且相等的四边形平行四边形).
2、有一块平行四边形的玻璃块,假如不小心碰碎了一部分,聪明的技师拿着细绳很快将原来的平行四边形画了出来,你知道他用的是什么方法吗?
A
C
B
提升练习
D
c
b
a
A’
C’
B’
a
c
b
设AB=a,BC=b,A C=c
(1)作△A’B’C’,使得A’B’=a,B’C’=b,A’ C’=c
(2)用圆规以A’为圆心,b为半径画弧,再以C’为圆心a为半径画弧,两弧交点为D,
(3)连接A’D,C’D,即可得□A’B’C’D.
两组对边分别相等的四边形为平行四边形
a
b
任选教室里不坐在同一直线上的三个同学作为一个平行四边形的三个顶点,那么第四个顶点是哪个座位的同学,请你站起来。
A
B
C
以三角形任两边为邻边作平行四边形可作3个。
A
D
B
C
D
A
B
C
A
B
C
D
提升练习
变式:
A
B
C
D
AB=DC AD=BC
AB∥DC AD∥BC
ABCD
∠ABC=∠ADC ∠BAD=∠BCD
判定一:
一组对边平行且相等的四边形是平行四边形
ABCD
ABCD
课堂小结
本节课学习了几个平行四边形判定方法?
判定二:
两组对边分部相等的四边形是平行四边形
判定三:
两组对角分部相等的四边形是平行四边形
