青岛版八年级数学下册 8.4 一元一次不等式组 课件(共15张PPT)
文档属性
| 名称 | 青岛版八年级数学下册 8.4 一元一次不等式组 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 344.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
8.4一元一次不等式组
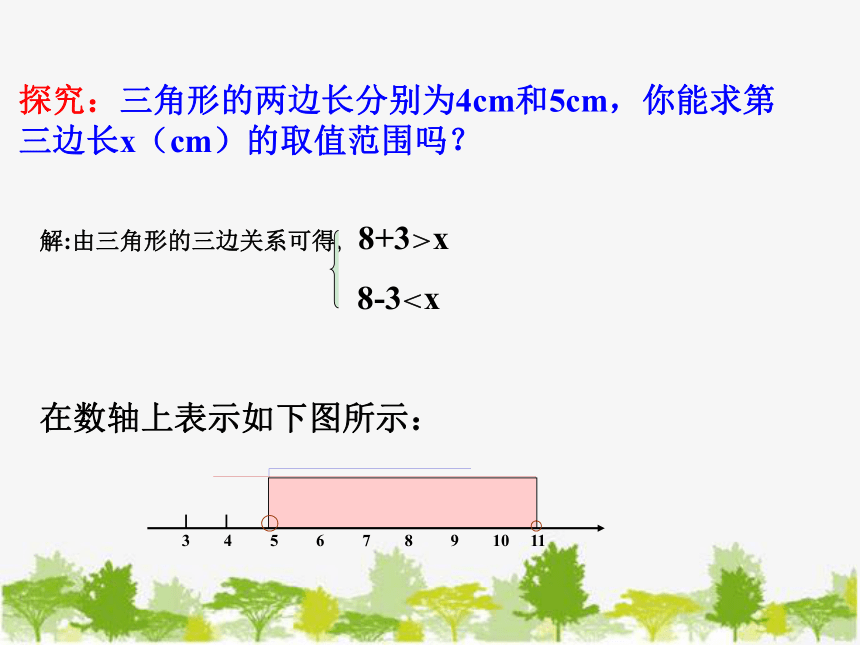
探究:三角形的两边长分别为4cm和5cm,你能求第三边长x(cm)的取值范围吗?
解:由三角形的三边关系可得, 8+3>x
8-3<x
在数轴上表示如下图所示:
3 4 5 6 7 8 9 10 11
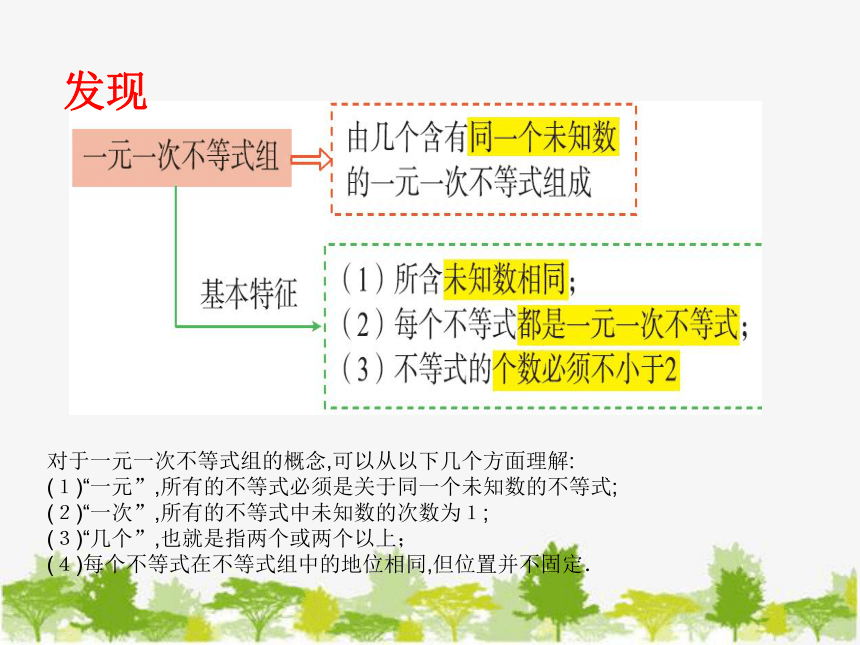
发现
对于一元一次不等式组的概念,可以从以下几个方面理解:
(1)“一元”,所有的不等式必须是关于同一个未知数的不等式;
(2)“一次”,所有的不等式中未知数的次数为1;
(3)“几个”,也就是指两个或两个以上;
(4)每个不等式在不等式组中的地位相同,但位置并不固定.
解不等式组
①
X+3>0
3x+4>12
②
6X+2<5
4x-1<4
2X+13<5
4x-1>8
④
X-4<2x+7
x+6>5
③
解一元一次不等式组的一般步骤:
1.求出这个不等式组中每个不等式的解集。
2.利用数轴求出这些不等式的解集的公共部分。
3.写出这个不等式组的解集;
练习
总结
一元一次不等式组解集在数轴上表示的四种情况
不等式组 数轴表示 解集
x>a
x>b
xxx>b
x>a
xb a
b a
b a
b a
无解
x>a
bxx同大取大
同小取小
“大”小“小”大 中间找
“大”大“小”小无处找
运用规律求下列不等式组的解集:
巧记口诀
1. 两大取大,
2.两小取小;
3.大小小大中间找,
4.大大小小无处找
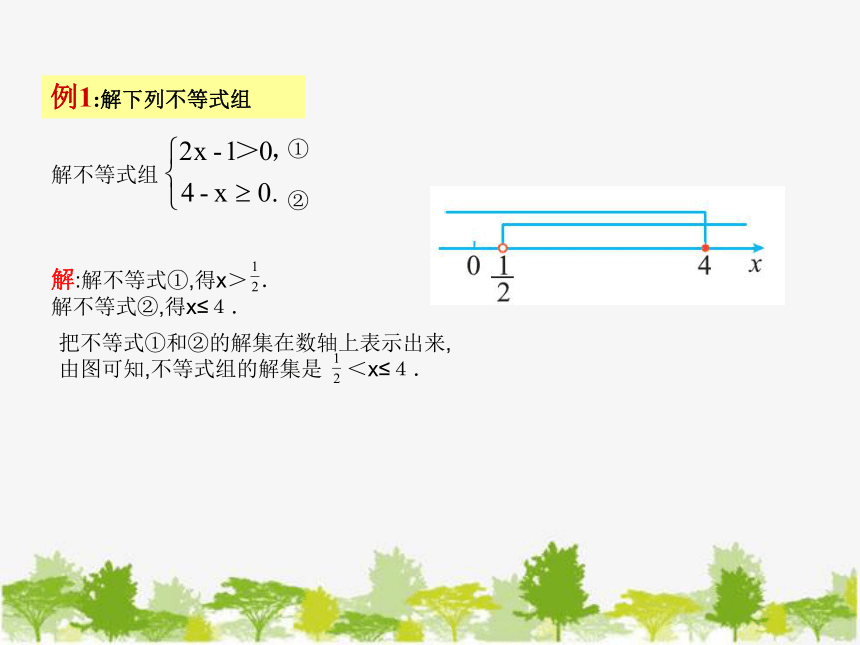
例1:解下列不等式组
①
解不等式组
②
解:解不等式①,得x> .
解不等式②,得x≤4.
把不等式①和②的解集在数轴上表示出来,
由图可知,不等式组的解集是 <x≤4.
1、解不等式组
2X-5≤5(x+1)
x-7≤5-
2、求不等式组 的解集
练习1
试求不等式组 的解集.
解:解不等式①,得 x > - 2
解不等式②,得 x > 5
解不等式③,得 x ≤ 8
把不等式①②③的解集表示在同一数轴上,如下图
-2 -1 0 1 2 3 4 5 6 7 8 9
○
●
○
所以,不等式组的解集是3 < x ≤ 6。
3x+6>0
x-5>0
2x-16≤0
例2
0 m 1 3/2 2
练习2若不等式组
有解,则m的取值范围是______。
解:化简不等式组得
根据不等式组解集的规律,得
因为不等式组有解,所以有
这中间的m当作数轴上的一个已知数
解不等式
例3
解:方法1:原不等式化为不等式组
①
②
解不等式①,得x≥-4;解不等式②,得x≤8.
所以不等式组的解集为-4≤x≤8,
即原不等式的解集为-4≤x≤8.
方法2:去分母,得 -9≤2x-1≤15.
移项,合并同类项,得 -8≤2x≤16.
系数化为1,得 -4≤x≤8.
解:2(x+1)-5<3(x-1)+4
解得x >-4
由题意x的最小整数解为x =-3
将x =-3代入方程 1/3 x-mx=5
解得 m=2
将m=2代入代数式 m -2m-11 =-11
练习3.若2(x+1)-5<3(x-1)+4的最小值是方程 x-mx=5 的解,求代数式m -2m-11的值.
3、关于不等式组 的解集是( )
2、若不等式组
的解集是-1<x<2,则m=____, n=____.
x+2>m
x-14、如果不等式组
的解集是x>m,则m_______。
x>m
x>n
1、在平面直角坐标系中,若 在第四象限,则的取值范围为( )
A. B. C. D.
A、m>8 B、m≥8 C、m<8 D、m≤8
5、关于x的不等式组
有解,那么m的取值范围是( )
x<8
x>m
练习
作业
8.4一元一次不等式组
探究:三角形的两边长分别为4cm和5cm,你能求第三边长x(cm)的取值范围吗?
解:由三角形的三边关系可得, 8+3>x
8-3<x
在数轴上表示如下图所示:
3 4 5 6 7 8 9 10 11
发现
对于一元一次不等式组的概念,可以从以下几个方面理解:
(1)“一元”,所有的不等式必须是关于同一个未知数的不等式;
(2)“一次”,所有的不等式中未知数的次数为1;
(3)“几个”,也就是指两个或两个以上;
(4)每个不等式在不等式组中的地位相同,但位置并不固定.
解不等式组
①
X+3>0
3x+4>12
②
6X+2<5
4x-1<4
2X+13<5
4x-1>8
④
X-4<2x+7
x+6>5
③
解一元一次不等式组的一般步骤:
1.求出这个不等式组中每个不等式的解集。
2.利用数轴求出这些不等式的解集的公共部分。
3.写出这个不等式组的解集;
练习
总结
一元一次不等式组解集在数轴上表示的四种情况
不等式组 数轴表示 解集
x>a
x>b
x
x>a
x
b a
b a
b a
无解
x>a
b
同小取小
“大”小“小”大 中间找
“大”大“小”小无处找
运用规律求下列不等式组的解集:
巧记口诀
1. 两大取大,
2.两小取小;
3.大小小大中间找,
4.大大小小无处找
例1:解下列不等式组
①
解不等式组
②
解:解不等式①,得x> .
解不等式②,得x≤4.
把不等式①和②的解集在数轴上表示出来,
由图可知,不等式组的解集是 <x≤4.
1、解不等式组
2X-5≤5(x+1)
x-7≤5-
2、求不等式组 的解集
练习1
试求不等式组 的解集.
解:解不等式①,得 x > - 2
解不等式②,得 x > 5
解不等式③,得 x ≤ 8
把不等式①②③的解集表示在同一数轴上,如下图
-2 -1 0 1 2 3 4 5 6 7 8 9
○
●
○
所以,不等式组的解集是3 < x ≤ 6。
3x+6>0
x-5>0
2x-16≤0
例2
0 m 1 3/2 2
练习2若不等式组
有解,则m的取值范围是______。
解:化简不等式组得
根据不等式组解集的规律,得
因为不等式组有解,所以有
这中间的m当作数轴上的一个已知数
解不等式
例3
解:方法1:原不等式化为不等式组
①
②
解不等式①,得x≥-4;解不等式②,得x≤8.
所以不等式组的解集为-4≤x≤8,
即原不等式的解集为-4≤x≤8.
方法2:去分母,得 -9≤2x-1≤15.
移项,合并同类项,得 -8≤2x≤16.
系数化为1,得 -4≤x≤8.
解:2(x+1)-5<3(x-1)+4
解得x >-4
由题意x的最小整数解为x =-3
将x =-3代入方程 1/3 x-mx=5
解得 m=2
将m=2代入代数式 m -2m-11 =-11
练习3.若2(x+1)-5<3(x-1)+4的最小值是方程 x-mx=5 的解,求代数式m -2m-11的值.
3、关于不等式组 的解集是( )
2、若不等式组
的解集是-1<x<2,则m=____, n=____.
x+2>m
x-1
的解集是x>m,则m_______。
x>m
x>n
1、在平面直角坐标系中,若 在第四象限,则的取值范围为( )
A. B. C. D.
A、m>8 B、m≥8 C、m<8 D、m≤8
5、关于x的不等式组
有解,那么m的取值范围是( )
x<8
x>m
练习
作业
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
