沪科版数学七年级下册 10.1相交线 教案
文档属性
| 名称 | 沪科版数学七年级下册 10.1相交线 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 146.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 10:23:40 | ||
图片预览

文档简介
《相交线》教案
教学目标
1、在具体情境中了解对顶角,能找出图形中的一个角的对顶角;
2、能运用“对顶角相等”进行简单的运算以及解决一些相关的实际问题.
3、了解垂直概念,能说出垂线的性质“经过一点,能画出已知直线的一条垂线,并且只能画出一条垂线”,会用三角尺或量角器过一点画一条直线的垂线.
教学重难点
重点:
对顶角的概念,对顶角的性质与应用.两条直线互相垂直的概念、性质和画法. “垂线段最短”的性质,点到直线的距离的概念及其简单应用.
难点:
对点到直线的距离的概念的理解.
教学过程
一.创设情境
课件展示图片,让学生观察、感受生活中的相交线.
想一想:这组图片有什么共同特点?引出课题,并介绍相交的概念.
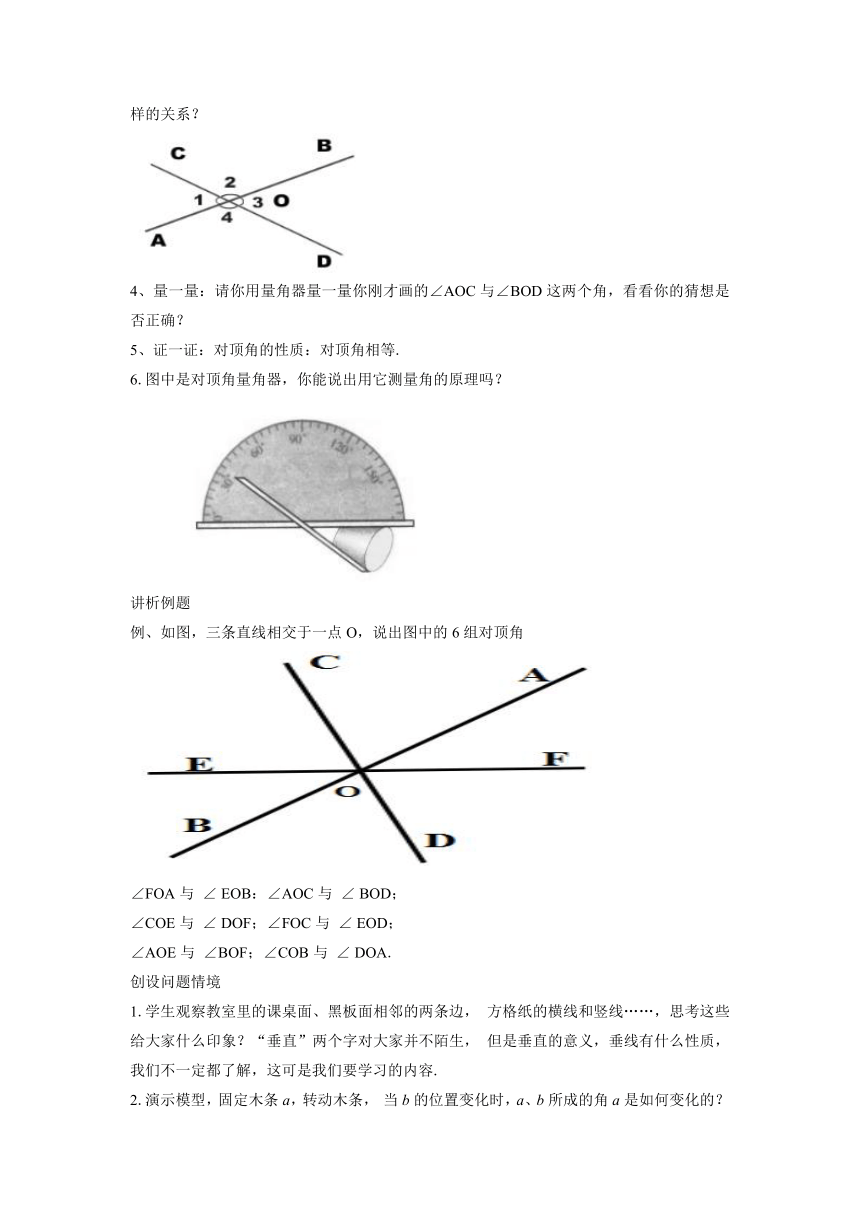
对顶角的概念:有一个公共顶点一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角.(找出图中的所有对顶角)
2.想一想:判断下列各图中∠1和∠2是否为对顶角,并说明理由?
3、猜一猜:请你猜一猜,剪刀剪东西的过程中,∠AOC和∠BOD这两个角的大小保持怎样的关系?
4、量一量:请你用量角器量一量你刚才画的∠AOC与∠BOD这两个角,看看你的猜想是否正确?
5、证一证:对顶角的性质:对顶角相等.
6.图中是对顶角量角器,你能说出用它测量角的原理吗?
讲析例题
例、如图,三条直线相交于一点O,说出图中的6组对顶角
∠FOA与 ∠ EOB:∠AOC与 ∠ BOD;
∠COE与 ∠ DOF;∠FOC与 ∠ EOD;
∠AOE与 ∠BOF;∠COB与 ∠ DOA.
创设问题情境
1.学生观察教室里的课桌面、黑板面相邻的两条边, 方格纸的横线和竖线……,思考这些给大家什么印象?“垂直”两个字对大家并不陌生, 但是垂直的意义,垂线有什么性质,我们不一定都了解,这可是我们要学习的内容.
2.演示模型,固定木条a,转动木条, 当b的位置变化时,a、b所成的角a是如何变化的?其中会有特殊情况出现吗?当这种情况出现时,a、b所成的四个角有什么特殊关系?
当b的位置变化时,角a从锐角变为钝角,其中∠a是直角是特殊情况.其特殊之处还在于:当∠a是直角时,它的邻补角,对顶角都是直角,即a、b所成的四个角都是直角,都相等.
3.给出垂直定义.
“互相垂直”与“垂线”的区别与联系:“互相垂直”指两条直线的位置关系;“垂线”是指其中一条直线对另一条直线的命名.如果说两条直线“互相垂直”时,其中一条必定是另一条的“垂线”, 如果一条直线是另一条直线的“垂线”,则它们必定“互相垂直”.
4.垂直的表示法.
垂直用符号“⊥”来表示,“直线AB垂直于直线CD,垂足为O”,则记为AB⊥CD,垂足为O,并在图中任意一个角处作上直角记号,如图.
画图实践,探究垂线的性质
1.用三角尺或量角器画已知直线L的垂线.
已知直线L(教师在黑板上画一条直线L),画出直线L的垂线,还能画出L的垂线吗?能画几条?直线L的垂线有无数多条,即存在,但有不确定性.
怎样才能确定直线L的垂线位置:在直线L上取一点A,过点A画L的垂线.
结论:经过直线上一点有且只有一条直线与已知直线垂直.
2.变式训练,巩固垂线的概念和画法,如图根据下列语句画图:
(1)过点P画射线MN的垂线,Q为垂足;
(2)过点P画射线BN的垂线,交射线BN反向延长线于Q点;
(3)过点P画线段AB的垂线,交线AB延长线于Q点.
问题:
1.在连接直线L外一点P与直线L 上各点的线段中,哪一条最短?
在硬纸板上固定木条L,L外一点P,转动的木条a一端固定在点P.
使木条L与a相交,左右摆动木条a,L与a的交点A随之变化,线段PA 长度也随之变化.PA最短时,a与L的位置关系如何?用三角尺检验.
2.画图操作,得出结论.
(1)画出直线L,L外一点P;
(2)过P点出PO⊥L,垂足为O;
(3)点A1,A2,A3……在L上,连接PA、PA2、PA3……;
(4)用叠合法或度量法比较PO、PA1、PA2、PA3……长短.
3.得出垂线的另一条性质.
连接直线外一点与直线上各点的所有线段中,垂线段最短,点到直线的距离.
根据两点间的距离的意义给出点到直线的距离命名.
认识垂线段PO:PO⊥L,∠POA=90°,O为垂足,垂线段PO的长度比其他线段PA1、PA2……中是最短的.
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
PO的长度是点P到直线L的距离,其余结论PA1、PA2……长度都不是点P到L的距离.
教学目标
1、在具体情境中了解对顶角,能找出图形中的一个角的对顶角;
2、能运用“对顶角相等”进行简单的运算以及解决一些相关的实际问题.
3、了解垂直概念,能说出垂线的性质“经过一点,能画出已知直线的一条垂线,并且只能画出一条垂线”,会用三角尺或量角器过一点画一条直线的垂线.
教学重难点
重点:
对顶角的概念,对顶角的性质与应用.两条直线互相垂直的概念、性质和画法. “垂线段最短”的性质,点到直线的距离的概念及其简单应用.
难点:
对点到直线的距离的概念的理解.
教学过程
一.创设情境
课件展示图片,让学生观察、感受生活中的相交线.
想一想:这组图片有什么共同特点?引出课题,并介绍相交的概念.
对顶角的概念:有一个公共顶点一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角.(找出图中的所有对顶角)
2.想一想:判断下列各图中∠1和∠2是否为对顶角,并说明理由?
3、猜一猜:请你猜一猜,剪刀剪东西的过程中,∠AOC和∠BOD这两个角的大小保持怎样的关系?
4、量一量:请你用量角器量一量你刚才画的∠AOC与∠BOD这两个角,看看你的猜想是否正确?
5、证一证:对顶角的性质:对顶角相等.
6.图中是对顶角量角器,你能说出用它测量角的原理吗?
讲析例题
例、如图,三条直线相交于一点O,说出图中的6组对顶角
∠FOA与 ∠ EOB:∠AOC与 ∠ BOD;
∠COE与 ∠ DOF;∠FOC与 ∠ EOD;
∠AOE与 ∠BOF;∠COB与 ∠ DOA.
创设问题情境
1.学生观察教室里的课桌面、黑板面相邻的两条边, 方格纸的横线和竖线……,思考这些给大家什么印象?“垂直”两个字对大家并不陌生, 但是垂直的意义,垂线有什么性质,我们不一定都了解,这可是我们要学习的内容.
2.演示模型,固定木条a,转动木条, 当b的位置变化时,a、b所成的角a是如何变化的?其中会有特殊情况出现吗?当这种情况出现时,a、b所成的四个角有什么特殊关系?
当b的位置变化时,角a从锐角变为钝角,其中∠a是直角是特殊情况.其特殊之处还在于:当∠a是直角时,它的邻补角,对顶角都是直角,即a、b所成的四个角都是直角,都相等.
3.给出垂直定义.
“互相垂直”与“垂线”的区别与联系:“互相垂直”指两条直线的位置关系;“垂线”是指其中一条直线对另一条直线的命名.如果说两条直线“互相垂直”时,其中一条必定是另一条的“垂线”, 如果一条直线是另一条直线的“垂线”,则它们必定“互相垂直”.
4.垂直的表示法.
垂直用符号“⊥”来表示,“直线AB垂直于直线CD,垂足为O”,则记为AB⊥CD,垂足为O,并在图中任意一个角处作上直角记号,如图.
画图实践,探究垂线的性质
1.用三角尺或量角器画已知直线L的垂线.
已知直线L(教师在黑板上画一条直线L),画出直线L的垂线,还能画出L的垂线吗?能画几条?直线L的垂线有无数多条,即存在,但有不确定性.
怎样才能确定直线L的垂线位置:在直线L上取一点A,过点A画L的垂线.
结论:经过直线上一点有且只有一条直线与已知直线垂直.
2.变式训练,巩固垂线的概念和画法,如图根据下列语句画图:
(1)过点P画射线MN的垂线,Q为垂足;
(2)过点P画射线BN的垂线,交射线BN反向延长线于Q点;
(3)过点P画线段AB的垂线,交线AB延长线于Q点.
问题:
1.在连接直线L外一点P与直线L 上各点的线段中,哪一条最短?
在硬纸板上固定木条L,L外一点P,转动的木条a一端固定在点P.
使木条L与a相交,左右摆动木条a,L与a的交点A随之变化,线段PA 长度也随之变化.PA最短时,a与L的位置关系如何?用三角尺检验.
2.画图操作,得出结论.
(1)画出直线L,L外一点P;
(2)过P点出PO⊥L,垂足为O;
(3)点A1,A2,A3……在L上,连接PA、PA2、PA3……;
(4)用叠合法或度量法比较PO、PA1、PA2、PA3……长短.
3.得出垂线的另一条性质.
连接直线外一点与直线上各点的所有线段中,垂线段最短,点到直线的距离.
根据两点间的距离的意义给出点到直线的距离命名.
认识垂线段PO:PO⊥L,∠POA=90°,O为垂足,垂线段PO的长度比其他线段PA1、PA2……中是最短的.
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
PO的长度是点P到直线L的距离,其余结论PA1、PA2……长度都不是点P到L的距离.
