华师大版数学七年级上册第3章整式的加减 单元小结(word版含答案)
文档属性
| 名称 | 华师大版数学七年级上册第3章整式的加减 单元小结(word版含答案) | 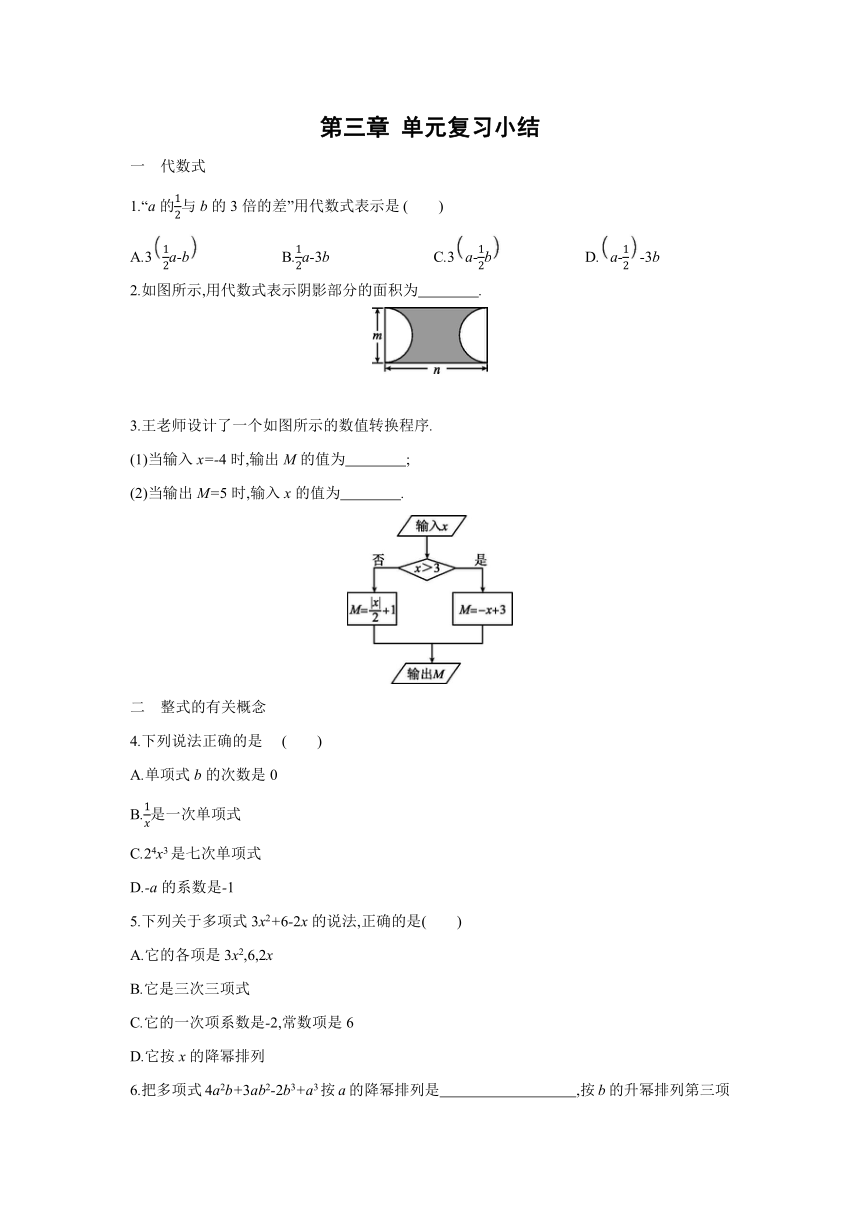 | |
| 格式 | docx | ||
| 文件大小 | 102.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 14:18:09 | ||
图片预览



文档简介
第三章 单元复习小结
一 代数式
1.“a的与b的3倍的差”用代数式表示是 ( )
A.3a-b B.a-3b C.3a-b D.a--3b
2.如图所示,用代数式表示阴影部分的面积为 .
3.王老师设计了一个如图所示的数值转换程序.
(1)当输入x=-4时,输出M的值为 ;
(2)当输出M=5时,输入x的值为 .
二 整式的有关概念
4.下列说法正确的是 ( )
A.单项式b的次数是0
B.是一次单项式
C.24x3是七次单项式
D.-a的系数是-1
5.下列关于多项式3x2+6-2x的说法,正确的是( )
A.它的各项是3x2,6,2x
B.它是三次三项式
C.它的一次项系数是-2,常数项是6
D.它按x的降幂排列
6.把多项式4a2b+3ab2-2b3+a3按a的降幂排列是 ,按b的升幂排列第三项是 .
7.如果单项式xa+1y3与2x3yb是同类项,那么ab= .
8.对于多项式(n-1)xm+2-3x2+2x(m,n为常数,且m是大于-2的整数).
(1)若n=2,且该多项式是关于x的三次三项式,求m的值;
(2)若该多项式化简后是关于x的二次单项式,求m,n的值;
(3)若该多项式化简后是关于x的二次二项式,则m,n满足什么条件
三 整式的加减运算
9.若单项式xm-1y3与4xyn的和仍是单项式,则nm的值是 ( )
A.3 B.6 C.8 D.9
10.若一个多项式减去a2-3b2等于a2+2b2,则这个多项式是 ( )
A.-2a2+b2 B.2a2-b2
C.a2-2b2 D.-2a2-b2
11.已知m-n=100,x+y=-1,则代数式(n+x)-(m-y)的值是 ( )
A.99 B.101 C.-99 D.-101
12.甲、乙、丙三人有相同数量的小球.如果甲给乙2颗,丙给甲5颗,然后乙再给丙一些球,所给的数量与丙还有的球数量相同,那么乙最后剩下 颗球.
13.先化简,再求值:2ab+6a2b+ab2-[3a2b-2(1-ab-2ab2)],其中a为最大的负整数,b为最小的正整数.
14.嘉淇准备完成题目:“化简(x2+6x+8)-(6x+5x2+2)”,发现系数印刷不清楚.
(1)她把“”猜成3,请你化简:(3x2+6x+8)-(6x+5x2+2);
(2)她妈妈说:“你猜错了,我看到该题的答案是常数.”通过计算说明原题中“”是几.
四 规律探索问题
15.有一组按规律排列的数:2,4,8,16,…,第2021个数应是 ( )
A.22020 B.22021-1
C.22021 D.以上选项均不对
16.[2020·重庆] 下列图形都是由同样大小的实心圆点按一定规律组成的,其中第①个图形一共有5个实心圆点,第②个图形一共有8个实心圆点,第③个图形一共有11个实心圆点……按此规律排列下去,第⑥个图形中实心圆点的个数为 ( )
A.18 B.19 C.20 D.21
17.[2020·海南改编] 海南黎锦有着悠久的历史,已被列入世界非物质文化遗产名录.如图是黎锦上的图案,每个图案都是由相同四边形构成的.若按照第1个图至第4个图中的规律编织图案,则第5个图中有 个四边形,第n个图中有 个四边形(n为正整数,用含n的代数式表示).
五 数学思想方法的应用
(整体思想)
18.当x=2时,代数式ax3-bx+2的值为3,那么当x=-2时,代数式ax3-bx+2的值是 ( )
A.-3 B.1 C.-1 D.2
19.已知当x=1时,2ax2+bx的值为3,则当x=2时,ax2+bx的值为 .
(转化思想)
20.如果a,b互为相反数,那么(5a2-10a)-5(a2+2b-3)的值为 ( )
A.-10 B.5 C.15 D.-15
21.已知A=5x2-mx-y+6,B=nx2-7x+3y-1,其中m,n为常数,若A-B化简后不含有x项和x2项,求3m+n2的值.
六 数学活动
22.请看以下扑克牌游戏:
小明背对小亮,让小亮按下列四个步骤操作:
第一步:分发左、中、右三堆牌,每堆牌的张数相同,且不少于两张;
第二步:从左边一堆拿出两张,放入中间一堆;
第三步:从右边一堆拿出一张,放入中间一堆;
第四步:左边一堆有几张牌,就从中间一堆拿几张牌放入左边一堆.
这时,小明准确说出了中间一堆牌现有的张数.你认为中间一堆牌现有的张数是多少 说明你的理由.
答案
1.B
2.mn- [解析] 阴影部分的面积=长方形的面积-2个半圆的面积=mn-.
3.(1)3 (2)-8 [解析] (1)因为x=-4<3,
所以M=+1=2+1=3.
故答案为:3.
(2)因为M=5,
所以+1=5(x≤3)或-x+3=5(x>3),
解得x=-8,
所以输入的x的值为-8.
故答案为:-8.
4.D 5.C 6.a3+4a2b+3ab2-2b3 3ab2
7.8 [解析] 因为单项式xa+1y3与2x3yb是同类项,所以a+1=3,b=3,解得a=2,b=3,则ab=23=8.
8.解:(1)因为n=2,且该多项式是关于x的三次三项式,
所以m+2=3,解得m=1.
(2)因为该多项式化简后是关于x的二次单项式,所以m+2=1,n-1=-2,
解得m=-1,n=-1.
(3)若该多项式是关于x的二次二项式,则有以下三种情况:
①n-1=0,m为大于-2的整数,则m,n满足的条件是n=1,m为大于-2的整数;
②m+2=1,且n-1≠-2,则m,n满足的条件是m=-1,n≠-1;
③m+2=2,且n-1≠3,则m,n满足的条件是m=0,n≠4.
9.D [解析] 因为xm-1y3与4xyn的和仍是单项式,所以xm-1y3与4xyn是同类项,所以m-1=1,n=3,解得m=2,n=3,所以nm=32=9.故选D.
10.B [解析] 因为一个多项式减去a2-3b2等于a2+2b2,所以这个多项式为a2-3b2+a2+2b2=2a2-b2.故选B.
11.D [解析] 因为m-n=100,x+y=-1,
所以原式=n+x-m+y=-(m-n)+(x+y)=-100-1=-101.故选D.
12.7 [解析] 设甲、乙、丙原来有a颗小球,
乙最后剩下的小球有a+2-(a-5)=a+2-a+5=7(颗).故答案为:7.
13.解:原式=2ab+3a2b+6ab2-3a2b+2-2ab-4ab2
=(2ab-2ab)+2+(3a2b-3a2b)+(6ab2-4ab2)
=2ab2+2.
因为a为最大的负整数,b为最小的正整数,
所以a=-1,b=1,所以原式=2×(-1)×12+2=0.
14.解:(1)(3x2+6x+8)-(6x+5x2+2)
=3x2+6x+8-6x-5x2-2
=-2x2+6.
(2)设“”是a,
则原式=(ax2+6x+8)-(6x+5x2+2)
=ax2+6x+8-6x-5x2-2
=(a-5)x2+6.
因为该题的答案是常数,所以a-5=0,
解得a=5,即原题中“”是5.
15.C [解析] 第1个数为2=21,
第2个数为4=22,
第3个数为8=23,
第4个数为16=24,
…
所以第2021个数为22021.
故选C.
16.C [解析] 因为第①个图形中实心圆点的个数为5=2×1+3,
第②个图形中实心圆点的个数为8=2×2+4,
第③个图形中实心圆点的个数为11=2×3+5,
……
所以第⑥个图形中实心圆点的个数为2×6+8=20.
故选C.
17.41 [n2+(n-1)2] [解析] 因为第1个图中四边形的个数为1=12+02,
第2个图中四边形的个数为5=22+12,
第3个图中四边形的个数为13=32+22,
第4个图中四边形的个数为25=42+32,
所以第5个图中四边形的个数为52+42=41,
第n个图中四边形的个数为n2+(n-1)2.
18.B
19.6 [解析] 将x=1代入2ax2+bx,得2a+b=3.将x=2代入ax2+bx,得4a+2b=2(2a+b).因为2a+b=3,所以原式=2×3=6.故答案 为6.
20.C [解析] 由a,b互为相反数,得到a+b=0,
则原式=5a2-10a-5a2-10b+15=-10(a+b)+15=15.
故选C.
21.解:A-B=5x2-mx-y+6-(nx2-7x+3y-1)=(5-n)x2-(m-7)x-4y+7.
因为A-B化简后不含有x项和x2项,
所以m-7=0,5-n=0,
解得m=7,n=5,
则3m+n2=21+25=46.
22.解:中间一堆牌现有的张数是5张.理由:设第一步的时候,每堆牌的数量都是x(x≥2)张;
第二步后:左边为(x-2)张,中间为(x+2)张,右边为x张;
第三步后:左边为(x-2)张,中间为(x+3)张,右边为(x-1)张;
第四步开始的时候,左边有(x-2)张牌,应从中间拿走(x-2)张,则中间所剩牌数为(x+3)-(x-2)=x+3-x+2=5(张).
所以中间一堆牌现有5张.
一 代数式
1.“a的与b的3倍的差”用代数式表示是 ( )
A.3a-b B.a-3b C.3a-b D.a--3b
2.如图所示,用代数式表示阴影部分的面积为 .
3.王老师设计了一个如图所示的数值转换程序.
(1)当输入x=-4时,输出M的值为 ;
(2)当输出M=5时,输入x的值为 .
二 整式的有关概念
4.下列说法正确的是 ( )
A.单项式b的次数是0
B.是一次单项式
C.24x3是七次单项式
D.-a的系数是-1
5.下列关于多项式3x2+6-2x的说法,正确的是( )
A.它的各项是3x2,6,2x
B.它是三次三项式
C.它的一次项系数是-2,常数项是6
D.它按x的降幂排列
6.把多项式4a2b+3ab2-2b3+a3按a的降幂排列是 ,按b的升幂排列第三项是 .
7.如果单项式xa+1y3与2x3yb是同类项,那么ab= .
8.对于多项式(n-1)xm+2-3x2+2x(m,n为常数,且m是大于-2的整数).
(1)若n=2,且该多项式是关于x的三次三项式,求m的值;
(2)若该多项式化简后是关于x的二次单项式,求m,n的值;
(3)若该多项式化简后是关于x的二次二项式,则m,n满足什么条件
三 整式的加减运算
9.若单项式xm-1y3与4xyn的和仍是单项式,则nm的值是 ( )
A.3 B.6 C.8 D.9
10.若一个多项式减去a2-3b2等于a2+2b2,则这个多项式是 ( )
A.-2a2+b2 B.2a2-b2
C.a2-2b2 D.-2a2-b2
11.已知m-n=100,x+y=-1,则代数式(n+x)-(m-y)的值是 ( )
A.99 B.101 C.-99 D.-101
12.甲、乙、丙三人有相同数量的小球.如果甲给乙2颗,丙给甲5颗,然后乙再给丙一些球,所给的数量与丙还有的球数量相同,那么乙最后剩下 颗球.
13.先化简,再求值:2ab+6a2b+ab2-[3a2b-2(1-ab-2ab2)],其中a为最大的负整数,b为最小的正整数.
14.嘉淇准备完成题目:“化简(x2+6x+8)-(6x+5x2+2)”,发现系数印刷不清楚.
(1)她把“”猜成3,请你化简:(3x2+6x+8)-(6x+5x2+2);
(2)她妈妈说:“你猜错了,我看到该题的答案是常数.”通过计算说明原题中“”是几.
四 规律探索问题
15.有一组按规律排列的数:2,4,8,16,…,第2021个数应是 ( )
A.22020 B.22021-1
C.22021 D.以上选项均不对
16.[2020·重庆] 下列图形都是由同样大小的实心圆点按一定规律组成的,其中第①个图形一共有5个实心圆点,第②个图形一共有8个实心圆点,第③个图形一共有11个实心圆点……按此规律排列下去,第⑥个图形中实心圆点的个数为 ( )
A.18 B.19 C.20 D.21
17.[2020·海南改编] 海南黎锦有着悠久的历史,已被列入世界非物质文化遗产名录.如图是黎锦上的图案,每个图案都是由相同四边形构成的.若按照第1个图至第4个图中的规律编织图案,则第5个图中有 个四边形,第n个图中有 个四边形(n为正整数,用含n的代数式表示).
五 数学思想方法的应用
(整体思想)
18.当x=2时,代数式ax3-bx+2的值为3,那么当x=-2时,代数式ax3-bx+2的值是 ( )
A.-3 B.1 C.-1 D.2
19.已知当x=1时,2ax2+bx的值为3,则当x=2时,ax2+bx的值为 .
(转化思想)
20.如果a,b互为相反数,那么(5a2-10a)-5(a2+2b-3)的值为 ( )
A.-10 B.5 C.15 D.-15
21.已知A=5x2-mx-y+6,B=nx2-7x+3y-1,其中m,n为常数,若A-B化简后不含有x项和x2项,求3m+n2的值.
六 数学活动
22.请看以下扑克牌游戏:
小明背对小亮,让小亮按下列四个步骤操作:
第一步:分发左、中、右三堆牌,每堆牌的张数相同,且不少于两张;
第二步:从左边一堆拿出两张,放入中间一堆;
第三步:从右边一堆拿出一张,放入中间一堆;
第四步:左边一堆有几张牌,就从中间一堆拿几张牌放入左边一堆.
这时,小明准确说出了中间一堆牌现有的张数.你认为中间一堆牌现有的张数是多少 说明你的理由.
答案
1.B
2.mn- [解析] 阴影部分的面积=长方形的面积-2个半圆的面积=mn-.
3.(1)3 (2)-8 [解析] (1)因为x=-4<3,
所以M=+1=2+1=3.
故答案为:3.
(2)因为M=5,
所以+1=5(x≤3)或-x+3=5(x>3),
解得x=-8,
所以输入的x的值为-8.
故答案为:-8.
4.D 5.C 6.a3+4a2b+3ab2-2b3 3ab2
7.8 [解析] 因为单项式xa+1y3与2x3yb是同类项,所以a+1=3,b=3,解得a=2,b=3,则ab=23=8.
8.解:(1)因为n=2,且该多项式是关于x的三次三项式,
所以m+2=3,解得m=1.
(2)因为该多项式化简后是关于x的二次单项式,所以m+2=1,n-1=-2,
解得m=-1,n=-1.
(3)若该多项式是关于x的二次二项式,则有以下三种情况:
①n-1=0,m为大于-2的整数,则m,n满足的条件是n=1,m为大于-2的整数;
②m+2=1,且n-1≠-2,则m,n满足的条件是m=-1,n≠-1;
③m+2=2,且n-1≠3,则m,n满足的条件是m=0,n≠4.
9.D [解析] 因为xm-1y3与4xyn的和仍是单项式,所以xm-1y3与4xyn是同类项,所以m-1=1,n=3,解得m=2,n=3,所以nm=32=9.故选D.
10.B [解析] 因为一个多项式减去a2-3b2等于a2+2b2,所以这个多项式为a2-3b2+a2+2b2=2a2-b2.故选B.
11.D [解析] 因为m-n=100,x+y=-1,
所以原式=n+x-m+y=-(m-n)+(x+y)=-100-1=-101.故选D.
12.7 [解析] 设甲、乙、丙原来有a颗小球,
乙最后剩下的小球有a+2-(a-5)=a+2-a+5=7(颗).故答案为:7.
13.解:原式=2ab+3a2b+6ab2-3a2b+2-2ab-4ab2
=(2ab-2ab)+2+(3a2b-3a2b)+(6ab2-4ab2)
=2ab2+2.
因为a为最大的负整数,b为最小的正整数,
所以a=-1,b=1,所以原式=2×(-1)×12+2=0.
14.解:(1)(3x2+6x+8)-(6x+5x2+2)
=3x2+6x+8-6x-5x2-2
=-2x2+6.
(2)设“”是a,
则原式=(ax2+6x+8)-(6x+5x2+2)
=ax2+6x+8-6x-5x2-2
=(a-5)x2+6.
因为该题的答案是常数,所以a-5=0,
解得a=5,即原题中“”是5.
15.C [解析] 第1个数为2=21,
第2个数为4=22,
第3个数为8=23,
第4个数为16=24,
…
所以第2021个数为22021.
故选C.
16.C [解析] 因为第①个图形中实心圆点的个数为5=2×1+3,
第②个图形中实心圆点的个数为8=2×2+4,
第③个图形中实心圆点的个数为11=2×3+5,
……
所以第⑥个图形中实心圆点的个数为2×6+8=20.
故选C.
17.41 [n2+(n-1)2] [解析] 因为第1个图中四边形的个数为1=12+02,
第2个图中四边形的个数为5=22+12,
第3个图中四边形的个数为13=32+22,
第4个图中四边形的个数为25=42+32,
所以第5个图中四边形的个数为52+42=41,
第n个图中四边形的个数为n2+(n-1)2.
18.B
19.6 [解析] 将x=1代入2ax2+bx,得2a+b=3.将x=2代入ax2+bx,得4a+2b=2(2a+b).因为2a+b=3,所以原式=2×3=6.故答案 为6.
20.C [解析] 由a,b互为相反数,得到a+b=0,
则原式=5a2-10a-5a2-10b+15=-10(a+b)+15=15.
故选C.
21.解:A-B=5x2-mx-y+6-(nx2-7x+3y-1)=(5-n)x2-(m-7)x-4y+7.
因为A-B化简后不含有x项和x2项,
所以m-7=0,5-n=0,
解得m=7,n=5,
则3m+n2=21+25=46.
22.解:中间一堆牌现有的张数是5张.理由:设第一步的时候,每堆牌的数量都是x(x≥2)张;
第二步后:左边为(x-2)张,中间为(x+2)张,右边为x张;
第三步后:左边为(x-2)张,中间为(x+3)张,右边为(x-1)张;
第四步开始的时候,左边有(x-2)张牌,应从中间拿走(x-2)张,则中间所剩牌数为(x+3)-(x-2)=x+3-x+2=5(张).
所以中间一堆牌现有5张.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
