华师大版数学八年级上册同步课时练习:13.4.3 作已知角的平分线(word版、含答案)
文档属性
| 名称 | 华师大版数学八年级上册同步课时练习:13.4.3 作已知角的平分线(word版、含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 164.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 00:00:00 | ||
图片预览


文档简介
13.4.3 作已知角的平分线
知识点 作已知角的平分线
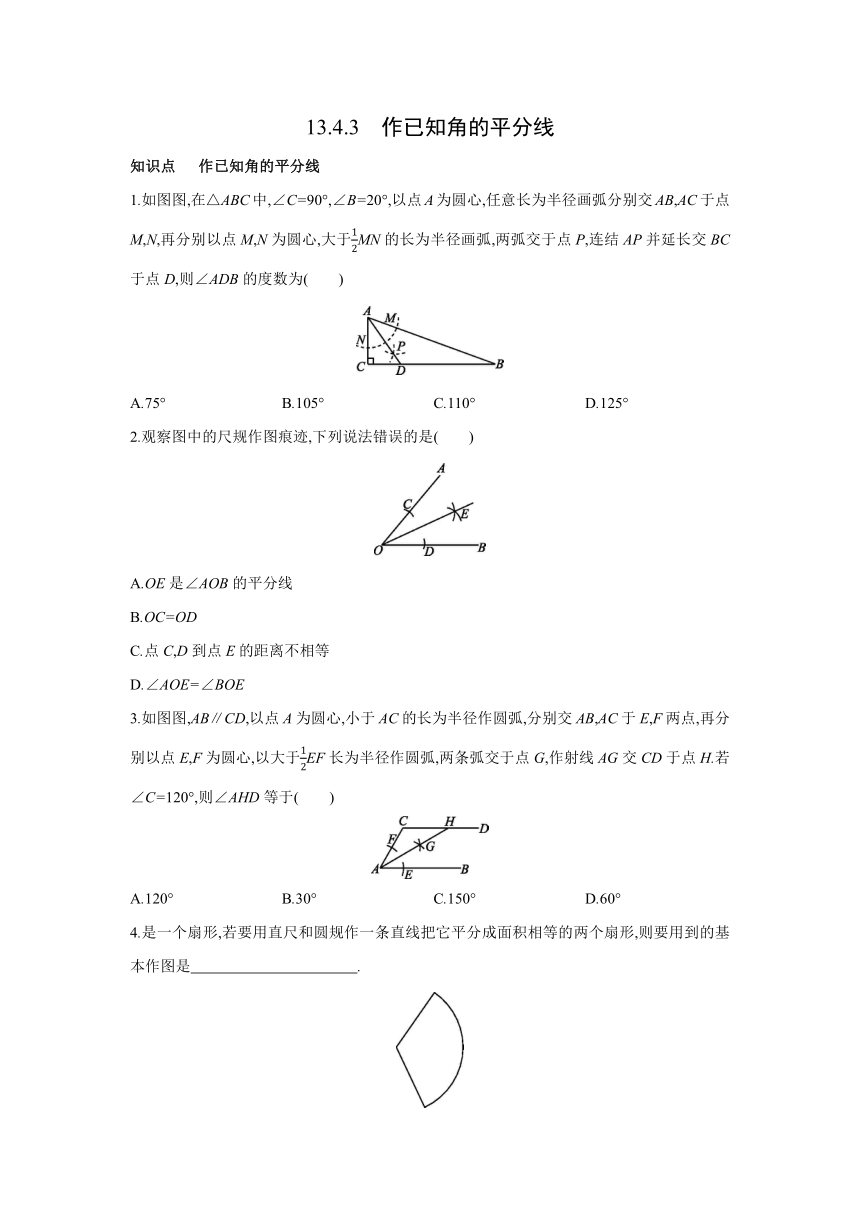
1.如图图,在△ABC中,∠C=90°,∠B=20°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则∠ADB的度数为( )
A.75° B.105° C.110° D.125°
2.观察图中的尺规作图痕迹,下列说法错误的是( )
A.OE是∠AOB的平分线
B.OC=OD
C.点C,D到点E的距离不相等
D.∠AOE=∠BOE
3.如图图,AB∥CD,以点A为圆心,小于AC的长为半径作圆弧,分别交AB,AC于E,F两点,再分别以点E,F为圆心,以大于EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H.若∠C=120°,则∠AHD等于( )
A.120° B.30° C.150° D.60°
4.是一个扇形,若要用直尺和圆规作一条直线把它平分成面积相等的两个扇形,则要用到的基本作图是 .
5.如图,在△ABC中,用直尺和圆规作∠ABC的平分线BD交AC于点D.(保留作图痕迹,不要求写作法)
6.[教材练习第1题变式] 如图所示,已知∠AOB,请在图中将∠AOB四等分.
7.如图,已知点D在△ABC的边AB上,且AD=CD.
(1)用直尺和圆规作∠BDC的平分线DE,交BC于点E(不写作法,保留作图痕迹);
(2)在(1)的条件下,判断DE与AC的位置关系,并说明理由.
8.如图所示,AB,AC表示两条相交公路,现要在∠BAC的内部建一个物流中心.设计时要求该物流中心在∠BAC的平分线上,且到公路交叉处点A的距离为1000米.
(1)若要以1∶50000的比例尺画设计图,求物流中心到公路交叉处点A的图上距离;
(2)在图中画出物流中心的位置P.
答案
1.D 由题中的作图步骤可得AD平分∠CAB.
∵∠C=90°,∠B=20°,
∴∠CAB=70°,
∴∠CAD=∠BAD=35°,
∴∠ADB=180°-20°-35°=125°.
故选D.
2.C
3.C 由作法得AH平分∠BAC,
则∠CAH=∠BAH.
∵AB∥CD,
∴∠BAC=180°-∠C=180°-120°=60°,
∴∠CAH=∠BAC=30°,
∴∠AHD=∠CAH+∠C=30°+120°=150°.
故选C.
4.作已知角的平分线
5.解:①以点B为圆心,以任意长为半径画弧,分别交AB,BC于点E,F;
②分别以点E,F为圆心,以大于EF的长为半径画弧,两弧相交于点G,作射线BG,BG交AC于点D.
6.解:作法:(1)作∠AOB的平分线OC;(2)分别作∠AOC,∠BOC的平分线OD,OE.
如图图所示.
7.解:(1)如图图所示,DE即为所求.
(2)DE∥AC.
理由:∵AD=CD,∴∠A=∠DCA,
∴∠BDC=∠A+∠DCA=2∠A.
∵DE平分∠BDC,∴∠BDC=2∠BDE,
∴∠BDE=∠A,∴DE∥AC.
8.解:(1)1000米=100000厘米,故物流中心到公路交叉处点A的图上距离为100000÷50000=2(厘米).
(2)如图图所示.
知识点 作已知角的平分线
1.如图图,在△ABC中,∠C=90°,∠B=20°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则∠ADB的度数为( )
A.75° B.105° C.110° D.125°
2.观察图中的尺规作图痕迹,下列说法错误的是( )
A.OE是∠AOB的平分线
B.OC=OD
C.点C,D到点E的距离不相等
D.∠AOE=∠BOE
3.如图图,AB∥CD,以点A为圆心,小于AC的长为半径作圆弧,分别交AB,AC于E,F两点,再分别以点E,F为圆心,以大于EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H.若∠C=120°,则∠AHD等于( )
A.120° B.30° C.150° D.60°
4.是一个扇形,若要用直尺和圆规作一条直线把它平分成面积相等的两个扇形,则要用到的基本作图是 .
5.如图,在△ABC中,用直尺和圆规作∠ABC的平分线BD交AC于点D.(保留作图痕迹,不要求写作法)
6.[教材练习第1题变式] 如图所示,已知∠AOB,请在图中将∠AOB四等分.
7.如图,已知点D在△ABC的边AB上,且AD=CD.
(1)用直尺和圆规作∠BDC的平分线DE,交BC于点E(不写作法,保留作图痕迹);
(2)在(1)的条件下,判断DE与AC的位置关系,并说明理由.
8.如图所示,AB,AC表示两条相交公路,现要在∠BAC的内部建一个物流中心.设计时要求该物流中心在∠BAC的平分线上,且到公路交叉处点A的距离为1000米.
(1)若要以1∶50000的比例尺画设计图,求物流中心到公路交叉处点A的图上距离;
(2)在图中画出物流中心的位置P.
答案
1.D 由题中的作图步骤可得AD平分∠CAB.
∵∠C=90°,∠B=20°,
∴∠CAB=70°,
∴∠CAD=∠BAD=35°,
∴∠ADB=180°-20°-35°=125°.
故选D.
2.C
3.C 由作法得AH平分∠BAC,
则∠CAH=∠BAH.
∵AB∥CD,
∴∠BAC=180°-∠C=180°-120°=60°,
∴∠CAH=∠BAC=30°,
∴∠AHD=∠CAH+∠C=30°+120°=150°.
故选C.
4.作已知角的平分线
5.解:①以点B为圆心,以任意长为半径画弧,分别交AB,BC于点E,F;
②分别以点E,F为圆心,以大于EF的长为半径画弧,两弧相交于点G,作射线BG,BG交AC于点D.
6.解:作法:(1)作∠AOB的平分线OC;(2)分别作∠AOC,∠BOC的平分线OD,OE.
如图图所示.
7.解:(1)如图图所示,DE即为所求.
(2)DE∥AC.
理由:∵AD=CD,∴∠A=∠DCA,
∴∠BDC=∠A+∠DCA=2∠A.
∵DE平分∠BDC,∴∠BDC=2∠BDE,
∴∠BDE=∠A,∴DE∥AC.
8.解:(1)1000米=100000厘米,故物流中心到公路交叉处点A的图上距离为100000÷50000=2(厘米).
(2)如图图所示.
