华师大版数学八年级上册同步课时练习:13.2.2 全等三角形的判定条件(word版、含答案)
文档属性
| 名称 | 华师大版数学八年级上册同步课时练习:13.2.2 全等三角形的判定条件(word版、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 181.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 20:33:05 | ||
图片预览


文档简介
13.2.1 全等三角形
13.2.2 全等三角形的判定条件
知识点 1 全等三角形
1.下列说法中,正确的有( )
①全等三角形对应顶点所对应的角是对应角;
②全等三角形对应顶点所对的边是对应边;
③全等三角形对应边所夹的角是对应角;
④全等三角形对应角所夹的边是对应边.
A.1个 B.2个
C.3个 D.4个
2.如图图,△ECD是由△ABC经过平移得到的,则△ ≌△ .
3.如图图,△ABC≌△ADE,∠B与∠D是对应角,AB与AD是对应边,另外两组对应边为 .
知识点 2 全等三角形的性质
4.有下列说法:①全等三角形的形状相同、大小相等;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等.其中正确的为( )
A.①②③④ B.①③④
C.①②④ D.②③④
5.如图图,△ABC≌△DEF,∠A=50°,∠B=100°,则∠F的度数是( )
A.100° B.60° C.50° D.30°
6.如图图所示,△ABC≌△DEF,请根据图中提供的信息,写出x= .
7.已知△ABC的三边长分别为3,5,7,△DEF的三边长分别为3,3x-2,2x-1,若这两个三角形全等,则x的值为 .
知识点 3 全等变换
8.如图图,△ABC绕点O旋转180°得到△A'B'C',则下列结论不成立的是( )
A.点A与点A'是对应点 B.∠ACB=∠C'A'B'
C.AB=A'B' D.BO=B'O
9.如图图所示,已知△ABC平移后得到△DEF,若∠A=80°,∠E=60°,求∠C的度数.
图
10.如图图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F处,如图果∠BAF=60°,那么∠DAE为多少度
图
知识点 4 探索三角形全等
11.下列说法中正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
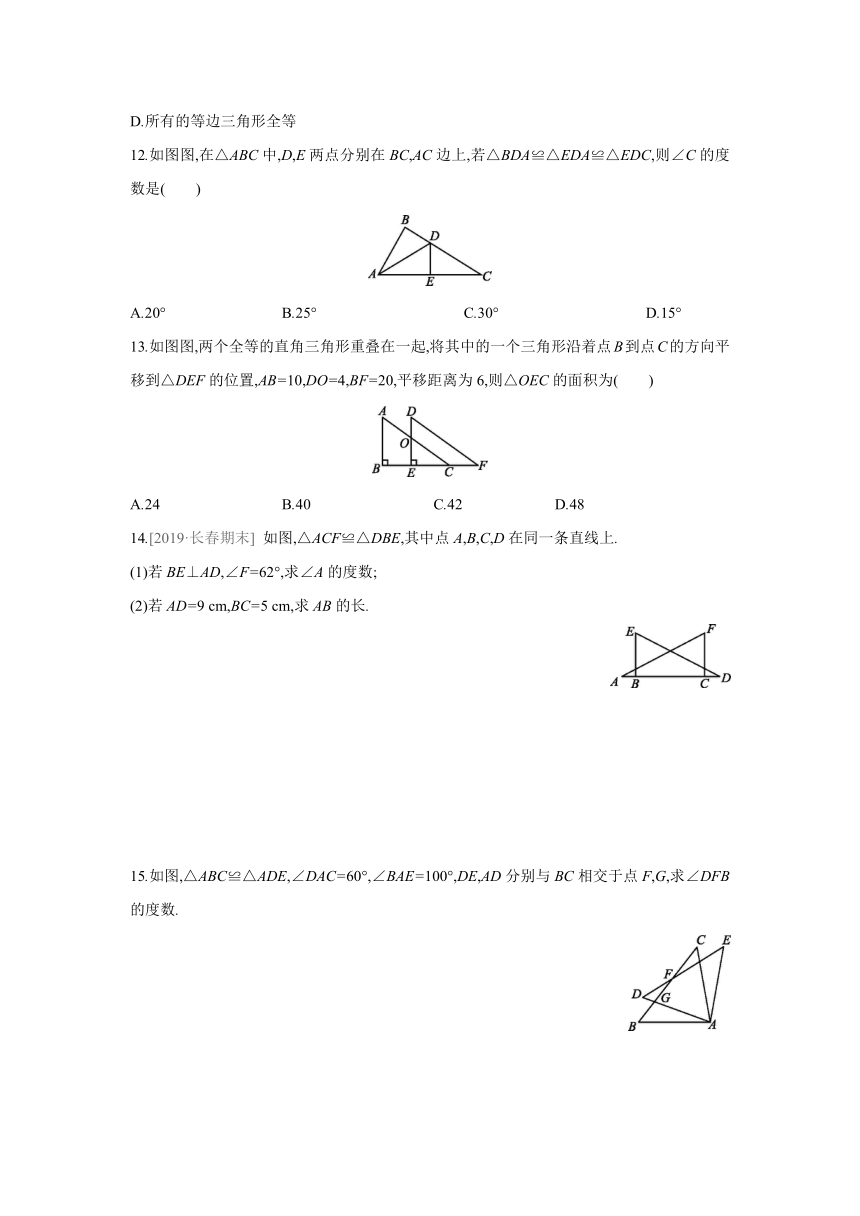
12.如图图,在△ABC中,D,E两点分别在BC,AC边上,若△BDA≌△EDA≌△EDC,则∠C的度数是( )
A.20° B.25° C.30° D.15°
13.如图图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DO=4,BF=20,平移距离为6,则△OEC的面积为( )
A.24 B.40 C.42 D.48
14.[2019·长春期末] 如图,△ACF≌△DBE,其中点A,B,C,D在同一条直线上.
(1)若BE⊥AD,∠F=62°,求∠A的度数;
(2)若AD=9 cm,BC=5 cm,求AB的长.
15.如图,△ABC≌△ADE,∠DAC=60°,∠BAE=100°,DE,AD分别与BC相交于点F,G,求∠DFB的度数.
16.如图所示,把△ABC纸片沿DE折叠,点A落在四边形BCDE内部的点A'处.
(1)写出图中一对全等的三角形,并写出它们所有的对应角;
(2)设∠AED的度数为x,∠ADE的度数为y,那么∠1,∠2的度数分别是多少(用含有x或y的代数式表示)
(3)∠A与∠1+∠2始终满足一种数量关系,请写出这一数量关系.
答案
1.D ①全等三角形对应顶点所对应的角是对应角,正确;②全等三角形对应顶点所对的边是对应边,正确;③全等三角形对应边所夹的角是对应角,正确;④全等三角形对应角所夹的边是对应边,正确.综上,正确的有①②③④,共4个.故选D.
2.ECD ABC
3.AC与AE,BC与DE 解题用到的知识点:全等三角形的对应边相等,对应角相等.根据“对应角对的边是对应边,对应边对的角是对应角”解题是正确解答本题的关键.
4.A
5.D ∵∠A=50°,∠B=100°,
∴∠C=180°-100°-50°=30°.
∵△ABC≌△DEF,
∴∠F=∠C=30°.
6.20 ∵△ABC≌△DEF,
∴EF=BC=20,即x=20.
7.3 ∵△ABC的三边长分别为3,5,7,△DEF的三边长分别为3,3x-2,2x-1,这两个三角形全等,
∴3+5+7=3+3x-2+2x-1,
解得x=3.
故答案为3.
8.B 旋转180°后,对应点与旋转中心共线,对应线段平行(或共线)且相等,对应点到旋转中心的距离相等,对应角相等,其中∠ACB与∠C'A'B'不是对应角,不能确定二者是否相等.
9. 由平移可知△ABC≌△DEF,∠ABC=∠E=60°,再根据三角形内角和定理可求得∠C的度数.
解:由平移的性质,得△ABC≌△DEF,
∴∠ABC=∠E=60°,
∴∠C=180BC=180°-80°-60°=40°.
10.解:∵四边形ABCD是长方形,∴∠BAD=90°.
∵长方形ABCD沿AE折叠,使点D落在BC边上的点F处,
∴△ADE≌△AFE,
∴∠DAE=∠FAE=∠DAF.
∵∠BAF=60°,
∴∠DAF=∠BAD-∠BAF=90°-60°=30°,
∴∠DAE=∠DAF=×30°=15°.
11.C A项,形状相同的两个三角形全等,错误,应该是形状相同、大小相等的两个三角形全等;
B项,面积相等的两个三角形全等,错误;
C项,完全重合的两个三角形全等,正确;
D项,所有的等边三角形全等,错误.
故选C.
12.C ∵△BDA≌△EDA≌△EDC,
∴∠B=∠DEA=∠DEC,
∠BAD=∠EAD=∠C.
∵∠DEA+∠DEC=180°,
∴∠DEA=∠DEC=90°=∠B.
又∵∠B+∠BAD+∠DAC+∠C=180°,
∴∠C=30°.
故选C.
13.A 由平移的性质知,BE=CF=6,
DE=AB=10,
∴OE=DE-DO=10-4=6.
∵BF=20,∴EC==8,
∴△OEC的面积=×6×8=24.
故选A.
14.解:(1)∵BE⊥AD,
∴∠EBD=90°.
∵△ACF≌△DBE,
∴∠FCA=∠EBD=90°,
∴∠A=90°-∠F=28°.
(2)∵△ACF≌△DBE,
∴CA=BD,
∴CA-BC=BD-BC,即AB=CD.
∵AD=9 cm,BC=5 cm,
∴AB+CD=9-5=4(cm),∴AB=2 cm.
15.解:∵△ABC≌△ADE,
∴∠B=∠D,∠BAC=∠DAE.
又∠BAD=∠BAC-∠DAC,
∠CAE=∠DAE-∠DAC,
∴∠BAD=∠CAE.
∵∠DAC=60°,∠BAE=100°,
∴∠BAD=(∠BAE-∠DAC)=×(100°-60°)=20°.
在△ABG和△FDG中,
∵∠B=∠D,∠AGB=∠FGD,
∴∠DFB=∠BAD=20°.
16.解:(1)△EAD≌△EA'D,∠EAD=∠EA'D,∠AED=∠A'ED,∠ADE=∠A'DE.
(2)∠1=180°-2x,∠2=180°-2y.
(3)∠1+∠2=2∠A.
13.2.2 全等三角形的判定条件
知识点 1 全等三角形
1.下列说法中,正确的有( )
①全等三角形对应顶点所对应的角是对应角;
②全等三角形对应顶点所对的边是对应边;
③全等三角形对应边所夹的角是对应角;
④全等三角形对应角所夹的边是对应边.
A.1个 B.2个
C.3个 D.4个
2.如图图,△ECD是由△ABC经过平移得到的,则△ ≌△ .
3.如图图,△ABC≌△ADE,∠B与∠D是对应角,AB与AD是对应边,另外两组对应边为 .
知识点 2 全等三角形的性质
4.有下列说法:①全等三角形的形状相同、大小相等;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等.其中正确的为( )
A.①②③④ B.①③④
C.①②④ D.②③④
5.如图图,△ABC≌△DEF,∠A=50°,∠B=100°,则∠F的度数是( )
A.100° B.60° C.50° D.30°
6.如图图所示,△ABC≌△DEF,请根据图中提供的信息,写出x= .
7.已知△ABC的三边长分别为3,5,7,△DEF的三边长分别为3,3x-2,2x-1,若这两个三角形全等,则x的值为 .
知识点 3 全等变换
8.如图图,△ABC绕点O旋转180°得到△A'B'C',则下列结论不成立的是( )
A.点A与点A'是对应点 B.∠ACB=∠C'A'B'
C.AB=A'B' D.BO=B'O
9.如图图所示,已知△ABC平移后得到△DEF,若∠A=80°,∠E=60°,求∠C的度数.
图
10.如图图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F处,如图果∠BAF=60°,那么∠DAE为多少度
图
知识点 4 探索三角形全等
11.下列说法中正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
12.如图图,在△ABC中,D,E两点分别在BC,AC边上,若△BDA≌△EDA≌△EDC,则∠C的度数是( )
A.20° B.25° C.30° D.15°
13.如图图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DO=4,BF=20,平移距离为6,则△OEC的面积为( )
A.24 B.40 C.42 D.48
14.[2019·长春期末] 如图,△ACF≌△DBE,其中点A,B,C,D在同一条直线上.
(1)若BE⊥AD,∠F=62°,求∠A的度数;
(2)若AD=9 cm,BC=5 cm,求AB的长.
15.如图,△ABC≌△ADE,∠DAC=60°,∠BAE=100°,DE,AD分别与BC相交于点F,G,求∠DFB的度数.
16.如图所示,把△ABC纸片沿DE折叠,点A落在四边形BCDE内部的点A'处.
(1)写出图中一对全等的三角形,并写出它们所有的对应角;
(2)设∠AED的度数为x,∠ADE的度数为y,那么∠1,∠2的度数分别是多少(用含有x或y的代数式表示)
(3)∠A与∠1+∠2始终满足一种数量关系,请写出这一数量关系.
答案
1.D ①全等三角形对应顶点所对应的角是对应角,正确;②全等三角形对应顶点所对的边是对应边,正确;③全等三角形对应边所夹的角是对应角,正确;④全等三角形对应角所夹的边是对应边,正确.综上,正确的有①②③④,共4个.故选D.
2.ECD ABC
3.AC与AE,BC与DE 解题用到的知识点:全等三角形的对应边相等,对应角相等.根据“对应角对的边是对应边,对应边对的角是对应角”解题是正确解答本题的关键.
4.A
5.D ∵∠A=50°,∠B=100°,
∴∠C=180°-100°-50°=30°.
∵△ABC≌△DEF,
∴∠F=∠C=30°.
6.20 ∵△ABC≌△DEF,
∴EF=BC=20,即x=20.
7.3 ∵△ABC的三边长分别为3,5,7,△DEF的三边长分别为3,3x-2,2x-1,这两个三角形全等,
∴3+5+7=3+3x-2+2x-1,
解得x=3.
故答案为3.
8.B 旋转180°后,对应点与旋转中心共线,对应线段平行(或共线)且相等,对应点到旋转中心的距离相等,对应角相等,其中∠ACB与∠C'A'B'不是对应角,不能确定二者是否相等.
9. 由平移可知△ABC≌△DEF,∠ABC=∠E=60°,再根据三角形内角和定理可求得∠C的度数.
解:由平移的性质,得△ABC≌△DEF,
∴∠ABC=∠E=60°,
∴∠C=180BC=180°-80°-60°=40°.
10.解:∵四边形ABCD是长方形,∴∠BAD=90°.
∵长方形ABCD沿AE折叠,使点D落在BC边上的点F处,
∴△ADE≌△AFE,
∴∠DAE=∠FAE=∠DAF.
∵∠BAF=60°,
∴∠DAF=∠BAD-∠BAF=90°-60°=30°,
∴∠DAE=∠DAF=×30°=15°.
11.C A项,形状相同的两个三角形全等,错误,应该是形状相同、大小相等的两个三角形全等;
B项,面积相等的两个三角形全等,错误;
C项,完全重合的两个三角形全等,正确;
D项,所有的等边三角形全等,错误.
故选C.
12.C ∵△BDA≌△EDA≌△EDC,
∴∠B=∠DEA=∠DEC,
∠BAD=∠EAD=∠C.
∵∠DEA+∠DEC=180°,
∴∠DEA=∠DEC=90°=∠B.
又∵∠B+∠BAD+∠DAC+∠C=180°,
∴∠C=30°.
故选C.
13.A 由平移的性质知,BE=CF=6,
DE=AB=10,
∴OE=DE-DO=10-4=6.
∵BF=20,∴EC==8,
∴△OEC的面积=×6×8=24.
故选A.
14.解:(1)∵BE⊥AD,
∴∠EBD=90°.
∵△ACF≌△DBE,
∴∠FCA=∠EBD=90°,
∴∠A=90°-∠F=28°.
(2)∵△ACF≌△DBE,
∴CA=BD,
∴CA-BC=BD-BC,即AB=CD.
∵AD=9 cm,BC=5 cm,
∴AB+CD=9-5=4(cm),∴AB=2 cm.
15.解:∵△ABC≌△ADE,
∴∠B=∠D,∠BAC=∠DAE.
又∠BAD=∠BAC-∠DAC,
∠CAE=∠DAE-∠DAC,
∴∠BAD=∠CAE.
∵∠DAC=60°,∠BAE=100°,
∴∠BAD=(∠BAE-∠DAC)=×(100°-60°)=20°.
在△ABG和△FDG中,
∵∠B=∠D,∠AGB=∠FGD,
∴∠DFB=∠BAD=20°.
16.解:(1)△EAD≌△EA'D,∠EAD=∠EA'D,∠AED=∠A'ED,∠ADE=∠A'DE.
(2)∠1=180°-2x,∠2=180°-2y.
(3)∠1+∠2=2∠A.
